Abstract
Digital markets provide firms with vast amounts of consumer data. Economists who have explored this phenomenon have focused on how firms use data to implement price discrimination. Targeted advertising in this context transmits different price information to different consumers. However, advertising is itself often valued by consumers, and can be viewed as a complement to the advertised product. Such advertising may also be customized and targeted. We investigate how targeted value-enhancing advertising affects competition. Competing for consumers with targeted advertising leads overall to higher prices and increases consumer surplus but reduces profitability. In certain markets the advertising is inefficiently over-supplied.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper examines a novel role for competitive advertising in the era of “big data” and unprecedented firm access to individual consumer information. Unlike much of the theoretical literature that investigates the use of such data to facilitate price discrimination and in which advertising is treated as largely informative our analysis views advertising as a complement to the advertised good: as in Becker and Murphy (1993). We take a further step and consider not only the possibility that firms may use consumer data to price discriminate but also use it to “version” their advertising. This is what we call targeted value-enhancing advertising.
Our paper builds on the idea that advertising has a direct effect on consumer utility when the consumer buys the advertised product. Our contribution is to recognize that if “big data” can provide firms with enough information to price discriminate, it may also provide firms with enough information to customize their value-enhancing advertising. We incorporate targeted value-enhancing advertising into a model of price and non-price market competition, while recognizing that providing value to consumers through targeted advertising is a costly activity.Footnote 1
We provide a brief literature review in the next section. In Sect. 3, we present our model of how firms target value-enhancing advertising to their customers, and then derive the market equilibrium outcomes—depending on whether firms implement price discrimination or set uniform prices. A summary and conclusion follow in Sect. 4.
2 Brief Literature Review
Prior work on targeted advertising and price discrimination largely focuses on how a firm’s acquisition of consumer data can enable it to differentiate consumers by: past buying behavior, Esteves (2009) and Esteves and Resende (2016); old versus new customers, Villas-Boas (1999); observed purchasing at other firms, Taylor (2004), Acquisti and Varian (2005); their “address” in product space Chen and Iyer, (2002); or time preference, Jing (2011).Footnote 2 Mikians et al. (2013) investigates empirical evidence on price discrimination that is based on location and user URL.Footnote 3
Targeted advertising in this earlier literature is viewed as a mechanism for transmitting (possibly different) product and price information to specific market segments: e.g., Esteban et al. (2003) and Iyer et al. (2005). Such advertising allows consumer demand to be realized or acted upon.Footnote 4
Our work differs from the work that is cited above in that we permit advertising to provide utility to consumers beyond that derived from simply consuming the good. Casual empirical evidence supports such an approach. Popular TV ads such as the Dos Equis “Most Interesting Man in the World” and Audi’s 2017 Super Bowl “Gender Pay Gap,” commercials offer very little product information. Instead, they aim to give viewers entertainment or a sense of shared social concern.Footnote 5
Similarly, AirBnB’s “Open Homes” and Budweiser’s “Clean Water” ads are not informative in the way that term is typically used. The ads appeal to a consumer’s philanthropic or environmental aspirations.Footnote 6 Consumers often share these ads on social media, and their remarks focus almost exclusively on the entertainment value and social sensibilities that the ads elicit.Footnote 7
Additional rough evidence that ads are increasingly valued largely for their non-informative content is that firms are now placing much more effort on the creative side of advertising. In the latter half of the twentieth century, roughly 10–20% of a firm’s advertising budget was spent on the creative side and 80–90% on media spending, whereas now the creative side accounts for about 45–55%.Footnote 8 Nike, for instance, was recently reported to spend 80% of its advertising budget on creative production efforts.Footnote 9
Formal empirical marketing research is also supportive: Tuchman et al. (2018) examine data that show both the number of ads to which a household was exposed and the number of ads that a household “skipped.” They find that ad-skipping is lower when the household has purchased more of the brand in the past. Lee et al. (2018) use a large-scale data set of FaceBook “likes” to measure consumer engagement with ads. They find that including emotional content has a significantly positive effect on subsequent consumer engagement.Footnote 10
3 The Model
We consider a duopoly market where each firm is located at the opposite end of a Hotelling (1929) line, set to unit length, and along which a mass of H consumers is uniformly distributed. Firm 1 is located at the left end of the line, and firm 2 is located at the right-most point. Each firm has incurred a sunk entry cost F to locate.
The “location” of consumer x typically identifies the consumer’s most preferred specification of product attributes. However, the location x could also be related to additional features of the consumer with regard to her likes and dislikes. A firm’s access to consumer data could provide it with this kind of additional information on the consumer who is located at x.
Targeted advertising refers to the customization of a firm’s promotion efforts. These differentiated promotional efforts are not necessarily related to the physical properties of the product. They could, for example, be related to personality traits or values of the consumer that affect her utility from consuming a brand. For example, brands such as Dove, Hellmanns, Ben & Jerry’s, and BP have each used advertising strategies that demonstrate the brand’s commitment to self-esteem and environmental protection in the hope that this will enhance consumer willingness to buy their advertised products.Footnote 11
Our model assumes that a firm’s advertising messages can be customized to consumers to enhance the consumption value of the good that is being marketed to them. We denote by αi(x) the advertising value that the firm i targets to consumer x, and we assume that the consumer’s utility function is separable and additive in \(\alpha _{i} \left( x \right)\) only when good i is purchased.
Consumer surplus from purchasing a firm’s product is:
V is the reservation price for the consumer’s preferred product specification, and t is a measure of the loss of utility per unit “distance” that the consumer incurs in buying a product other than the one with the most preferred specification. We assume that V > \(\frac{3}{2}\) t > 0 and that each consumer buys one unit of the product that offers the greatest consumer surplus.Footnote 12
It is important to recognize that \(\alpha _{i} \left( x \right)\) is not the number of ads expended on consumer x by firm i. Rather, it is the value of advertising that consumer x enjoys if the consumer buys firm i's good. Consumer utility from the targeted advertising does not depend on the parameter t. That parameter instead reflects the disutility of consuming a good whose physical attributes differ from the consumer’s most preferred version.
The unit cost c of production is assumed to be identical across the two firms and without loss of generality is normalized to zero. Targeted advertising, on the other hand, is costly. The cost of targeted advertising reflects underlying decreasing returns as it is increasing costly to add value to the consumption experience. These costs are incurred and sunk before a transaction with a consumer take place.
Specifically, firm i’s cost of creating targeted advertising value \(\alpha _{i} (x\)) is:
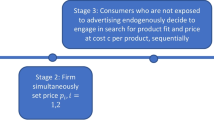
We adopt a three-stage game that captures how advertising is a cost that is sunk before transactions take place. In the first stage firm i (i = 1, 2) offers targeted advertising and a price to each of its potentially most brand-loyal consumers: those consumers for whom firm i’s good is relatively closer to their own most-preferred version. These are consumers \(~x:0 \le x \le \frac{1}{2}\) for firm 1; and \(\frac{1}{2} \le x \le 1\) for firm 2. In this initial stage, the costs of advertising to these consumers are incurred, and the firms commit to the prices that are offered to these potentially brand-loyal consumers. In the second stage, a firm may incur additional advertising costs and target consumers in the rival firm’s market segment. Consumers make their purchase decisions in stage 3.
We investigate market equilibria under three different pricing regimes: The first is where each firm commits to a uniform price to all consumers that it serves in stage 3, but the firms can target their value-enhancing advertising. The second case is where each firm can price discriminate and also target value-enhancing advertising. The third case is where each firm is restricted to offer the same value of advertising and the same price to each consumer served.Footnote 13
3.1 Targeted Advertising Under Uniform Pricing
In stage 1 each firm i sets a uniform price \(p_{i}\) and sends customized advertising \(a_{i} \left( x \right)~\) to consumer x in its segment of the market: for firm 1, 0 ≤ x ≤ \(\frac{1}{2}\); for firm 2, \(\frac{1}{2}~\)≤ x < 1. Each firm knows that the rival firm can use targeted advertising in stage 2 to poach customers from its segment of the market. In stage 3 consumers make their purchase decisions. We sketch out the argument for what are the profit-maximizing strategies that are adopted by the two firms in stage 1 and 2:
Consider firm 2 as the rival firm in stage 2. Given the prices \(p_{1}\), \(p_{2}\) that are set in stage 1 and firm 1’s advertising strategies \(a_{1} \left( x \right)\) for 0 ≤ x ≤ \(\frac{1}{2}\) firm 2 can try to poach a consumer x, 0 ≤ x < \(\frac{1}{2}\), by expending resources on advertising and offering a value \(a_{2} \left( {x;p_{1} ,{\text{~}}p_{2} } \right)~\) that is attractive to the consumer. For firm 2’s offer to succeed in attracting consumer x to buy its more “distant” product: \(a_{2} \left( {x;p_{1} ,{\text{~}}p_{2} } \right) = p_{2} - p_{1} + a_{1} \left( x \right) + t\left( {1 - 2x} \right)\).
The maximum \(\hat{a}_{2} \left( {x;p_{1} ,{\text{~}}p_{2} } \right)\) that firm 2 can offer consumer x in stage 2 must also satisfy its profitability constraint, \(p_{2} - [a_{2} \left( {x;p_{1} ,{\text{~}}p_{2} } \right)]^{2} = 0\). This implies a maximum value \(\hat{a}_{2} \left( {p_{2} } \right) = \sqrt {p_{2} }\). For firm 1 to be able to serve consumer x in stage 3, the firm must in stage 1 pre-empt this potential offer in stage 2 from its rival. Accordingly, firm 1 must offer consumer x in stage 1:
If firm 1 offers \(a_{1}^{*} \left( {x;p_{1} ,p_{2} } \right)\) at \(p_{1}\) to consumer x, 0 ≤ x < \(\frac{1}{2}\), in stage 1, it is not profitable for firm 2 to use costly advertising in stage 2 to attract this consumer. Firm 2’s best response to firm 1’s strategy in stage 1 is not to target consumer x in stage 2: \(a_{2}^{*} \left( {x;p_{1} ,{\text{~}}p_{2} } \right) = 0\), for \(0 \le x \le \frac{1}{2}\).
A similar argument for firm 1, as the rival in stage 2, can be made with regard to its ability to use targeted advertising to poach consumers from firm 2’s segment: \(\frac{1}{2}~\)≤ x < 1. This argument implies that firm 2 offers in stage 1 advertising \(a_{2}^{*} \left( {x;p_{1} ,p_{2} } \right) = p_{2} - p_{1} + \sqrt {p_{1} } + t\left( {1 - 2x} \right)\) to consumer x, where \(\frac{1}{2}~\)≤ x < 1. This offer makes it unprofitable for firm 1 to use advertising to attract these consumers in stage 2.
In stage 1, the firms simultaneously choose price, and hence the value of the advertising that is targeted to the consumers for whom they have a locational advantage. Suppose initially that each firm i offers a positive targeted value \(a_{i}^{*} \left( {x,p_{1} ,p_{2} } \right) > 0~\) to all consumers x on its segment of the market. If \(a_{1}^{*} \left( {x,p_{1} ,p_{2} } \right) > 0,{\text{~}}\) 0 < x < \(\frac{1}{2}\), firm 1 chooses in stage 1 a price \(p_{1}\) to maximize:
The first order necessary condition for firm 1’s maximization of (4) is:
In stage 1, firm 2 behaves symmetrically, and hence we have:
When \(a_{i}^{*} \left( {x;p_{1} ,p_{2} } \right) > 0\) for all 0 ≤ x < 1, i = 1,2, the equilibrium uniform prices that are set by the firms.
in stage 1 are:
Equations (3) and (7) together imply that if t = 1, consumers at x = 0 (and by symmetry, those at x = 1) receive no targeted advertising: \(a_{i}^{*} \left( 0 \right) = a_{i}^{*} \left( 1 \right) = 0\). This suggests that as t rises above 1, the range of consumers receiving no targeted advertising increases, and our supposition that \(a_{i}^{*} \left( {x,p_{1} ,p_{2} } \right) > 0~\) for 0 < x < 1 will not hold. To state this result somewhat differently, a necessary and sufficient condition for that \(a_{i}^{*} \left( {x,p^{*} } \right) > 0\) for all consumers x is that 0 < t < 1.
The intuition for the above result is clear: As preferences for differentiation – as is indexed by t become stronger, the value of the targeted advertising that a firm that is without a locational advantage must offer to poach a rival’s most loyal consumers rises. By (3) the costs of increasing targeted advertising also increase. When t = 1, the cost of targeted advertising is such that firm 2 as the rival firm cannot profitably poach consumers at x = 0; and similarly, firm 1 cannot profitably poach consumers at x = 1. Given this, firm 1 does not need to offer in stage 1 any targeted advertising to consumers at x = 0 and similarly, firm 2 does need to offer targeted advertising to consumers at x = 1. As t increases t > 1 the range of customers that each firm can retain without offering any value enhancing advertising also grows.
The foregoing implies that to characterize the targeted advertising and price equilibrium when t > 1, we must identify each firm’s consumers who cannot be poached by the rival firm’s advertising. Alternatively, a firm needs to offer targeted value-enhancing advertising only to those consumers who are at risk of being poached by the rival firm. When t > 1, an offer by firm 1 of \(a_{1}^{*} \left( {x,p_{1} ,p_{2} } \right) > 0\) to a consumer x, \(0 < x \le \frac{1}{2},~\) implies that \(x > \left[ {\frac{1}{2} - \frac{{\left( {p_{1} + \sqrt {p_{2} } - p_{2} } \right)}}{{2t}}} \right] = \hat{x}\left( {p_{1} ,~p_{2} } \right)\). In stage 3, firm 1 can retain those consumers x whose locational preference is 0 < x < \(\hat{x}\left( {p_{1} ,~p_{2} } \right)\) without offering any advertising. Even the maximally affordable level of advertising that it could offer – \(\hat{a}_{2} \left( {{\text{~}}p_{2} } \right) = \sqrt {p_{2} }\) – would not induce these consumers to buy firm 2’s brand at price \(p_{2} .\)
When t > 1, firm 1 chooses in stage 1 a price \(p_{1}\) to maximize:
The first-order necessary condition of (8) leads to a best response:
Firm 2 behaves symmetrically in stage 1 with respect to its rival, and chooses:
Solving for the prices for this case \(~p_{1}^{*} = p_{2}^{*} = p^{*} ,\) we find \(p^{*} = t\).Footnote 14
The complete range of equilibrium outcomes for uniform pricing and targeted value-enhancing advertising can be broken down into two subsets: One corresponds to product differentiated markets for which \(0 < t \le 1\); and the other corresponds to \(t > 1\). These are summarized in Propositions 1(a),and 1(b):
Proposition 1(a)
For V ≥ \(~\frac{3}{2}\) t, and 0 < t ≤ 1, the following strategies support a perfect equilibrium:
S1: Firm 1 offers consumer x, 0 ≤ x < \(\frac{1}{2}\), \(a_{1}^{*} \left( x \right) = \frac{1}{2}\) \(- \frac{t}{2} + 2tx~~\) at \(p_{1}^{*} = \frac{{\left( {1 + t} \right)^{2} }}{4}\).
Firm 2 offers consumer x, \(\frac{1}{2}\) < x < 1, \(a_{2}^{*} \left( x \right) = \frac{1}{2}\) \(+ \frac{{3t}}{2} - 2tx~\) at \(p_{2}^{*} = \frac{{\left( {1 + t} \right)^{2} }}{4}\).
S2: Firm 1 offers consumer x, \(\frac{1}{2}\) < x < 1, \(a_{1}^{*} \left( x \right) = 0\) at \(p_{1}^{*} = \frac{{\left( {1 + t} \right)^{2} }}{4}\).
Firm 2 offers consumer x, 0 ≤ x < \(\frac{1}{2}\), \(a_{2}^{*} \left( x \right) = 0\) at \(p_{1}^{*} = \frac{{\left( {1 + t} \right)^{2} }}{4}\).
S3: Consumer x, 0 ≤ x < \(\frac{1}{2}~,\) purchases brand 1; consumer x, \(\frac{1}{2}~\) < x ≤ \(1\), purchases brand 2;
Consumer x = \(\frac{1}{2}\) with equal probability purchases brand 1 or 2.
Observe that when t = 0 and the two products are perfect substitutes Proposition 1(a) explains how the targeted advertising strategies of the two firms differentiates the two products. When t = 0 each consumer x enjoys targeted advertising value from the brand that the consumer buys, and the advertising enhances the value of the brand that she buys by \(a^{*} = \frac{1}{2}\). The price that is charged covers the sunk cost of advertising. and each firm earns zero profit in this highly competitive equilibrium. When t = 0, it is not feasible to cover any fixed cost F.
when 1 > t > 0 and consumer preferences for the differentiation of product attributes is relatively weak, a firm targets value-enhancing customized advertising to all those consumers whose most preferred version of the good lies closer to its brand than to its rival’s brand. However, the value of the targeted advertising that is sent to a consumer rises as that consumer’s most preferred good lies farther from the advertising firm. Firms compete in targeted advertising most heavily for those consumers near the middle of the product market with the weakest preferences for the physical attributes of either firm’s product.
The average amount of advertising that is offered by a firm to its customers (when 1 > t > 0) is \(\bar{a} = \frac{1}{2}\). Each firm earns positive profit \(\pi ^{{1a}} \left( t \right) = H\left[ {\frac{t}{4}\left( {1 + \frac{t}{3}} \right)} \right] - F\). This is less than the duopoly profit \(H\frac{t}{2} - F\) that is earned under uniform pricing in the standard (Hotelling) model with no advertising. Consumer surplus with targeted advertising and uniform pricing is \(CS^{{1a}} = H\left[ {V - \frac{3}{4}t + \frac{1}{4} - \frac{{t^{2} }}{4}} \right]\), which is greater.
than the standard Hotelling consumer surplus \(H\left[ {V - \frac{5}{4}t} \right]\). Using customized advertising to compete helps consumers but hurts producers. The overall effect is a net increase in the total welfare \(TS^{{1\left( a \right)}} = H\left[ {V - \frac{t}{4} + \frac{1}{4} - \frac{{t^{2} }}{{12}}} \right] - F\) \(> ~H\left[ {V - \frac{t}{4}} \right] - F\).
Proposition 1(b)
For V ≥ \(~\frac{3}{2}\) t, and t > 1, the following strategies support a perfect equilibrium:
S1: Firm 1 offers: \(a_{1}^{*} \left( x \right) = 0\) at \(p_{1}^{*} = t\) to consumer x, \(0 \le x \le \hat{x},\) where \(\hat{x} = \frac{1}{2} - \frac{1}{{2\sqrt t }}~\), and \(a_{1}^{*} \left( x \right) = \sqrt t - t + 2tx~{\text{at}}~p_{1}^{*} = t\) to consumers x, \(\hat{x}~\) < x < \(\frac{1}{2}\).
Firm 2 offers: \(a_{2}^{*} \left( x \right) = \sqrt t + t - 2tx~\) at \(p_{2}^{*} = t\) to consumer x, \(\frac{1}{2}\) < x < \(\left( {1 - \hat{x}^{'} } \right),\) where.
\(\hat{x}^{'} = \frac{1}{2} + \frac{1}{{2\sqrt t }},\) and \(a_{2}^{*} \left( x \right) = 0~{\text{at}}~p_{1}^{*} = t\) to consumer x, \(\left( {1 - \hat{x}^{'} } \right)~\) < x < 1.
S2: Firm 1 offers to consumer x, \(\frac{1}{2}~\) < x ≤ \(1\) \(a_{1}^{*} \left( x \right) = 0\) at \(p_{1}^{*} = t\).
Firm 2 offers to consumer x, 0 ≤ x < \(\frac{1}{2}\) \(a_{2}^{*} \left( x \right) = 0\) at \(p_{2}^{*} = t\).
S3: Consumer x, 0 ≤ x < \(\frac{1}{2},\) purchases brand 1, consumer x, \(\frac{1}{2}~\) < x ≤ \(1\), brand 2.
Consumer x = \(\frac{1}{2}\) buys with equal probability brand 1 or 2.
For all cases, when t > 1 – including the Hotelling (1929) benchmark case of uniform pricing and no targeted advertising—firm profitability does increase with t. However, the competition in targeted advertising does reduce each firm’s profit below that of the Hotelling case of uniform pricing and no targeted advertising: \(\pi ^{{1b}} \left( t \right) = \frac{{H\sqrt t }}{2}\left( {\sqrt t - \frac{1}{3}} \right) - F < ~H\frac{t}{2} - F\).
Consumer surplus when t > 1 is \(CS^{{1b}} = H\left[ {V - \frac{{5t}}{4} + \frac{1}{2}} \right]\). Again, consumer surplus is greater than in the benchmark Hotelling (1929) case. When firms compete in value-enhancing advertising, consumers are better off. Essentially, the firms have “discovered” a complementary service that consumers value. However, when t > 1, this gain in consumer surplus is concentrated on a subset of consumers who receive targeted advertising and are located nearer the center of the market where competition with the rival is greatest.
When t > 1 and firms cannot discriminate in pricing but can discriminate in advertising, there is a potential for market inefficiency.Footnote 15 Producer surplus in this case is \(H\sqrt t \left( {\sqrt t - \frac{1}{3}} \right)\), and total surplus is \(H\left[ {V - \frac{t}{4} - \frac{{\sqrt t }}{3} + \frac{1}{2}} \right]\). Comparison with the total surplus in the Hotelling (1929) benchmark case —\(H\left[ {V - \frac{t}{4}} \right]\) reveals that for \(t > \frac{9}{4}\), the total surplus when firms set a uniform price but target their advertising is less than that benchmark case. The intuition that underlies this result is subtle:
In all uniform-pricing cases including Hotelling’s (1929) model increases in t reduce consumer surplus but raise producer surplus: The former effect dominates, so that increases in t reduce the total surplus. When \(t > 1,\) the decrease in consumer surplus that is due to an increase in t is the same whether firms also offer value-enhancing advertising or, as in the Hotelling (1929) case, do not. However, the countervailing increase in firm profit is less. The underlying intuition is: As t increases above 1, firms incur the cost of focusing their targeted advertising on a progressively smaller range of consumers. If firms were able to discriminate in prices, they might compete for this subset of consumers with selective price cuts that do not require costly resources.Footnote 16 However, the firms are constrained to set uniform prices. In brief, targeted advertising can be inefficiently excessive when \(t > \frac{9}{4}\).
It is worth noting that our model’s equilibrium outcomes are consistent with Sutton’s (1991) suggestion that endogenous sunk advertising costs imply a lower bound to market concentration in some consumer product markets, such as beverages, household detergents, and frozen foods. In our model, targeted advertising leads firms to incur sunk advertising costs that reduce their profitability relative to the standard, no-targeted-advertising case. Hence, firms have an incentive to exploit scale economies in production and reap advantages in their advertising exactly as Sutton (1991) argued.
3.2 Targeted Advertising with Price Discrimination
Suppose now that the two firms can implement discriminatory pricing as well as targeted value-enhancing advertising. In stage 1, each firm again incurs the sunk costs of such advertising and offers that advertising along with its product at a targeted price to each consumer with a relative locational preference for that firm’s good. In stage 2 each firm can use both value-enhancing advertising and a targeted (discriminatory) price to poach consumers from its rival’s segment of the market. Consumers make their purchases in stage 3.
In stage 1 firm 1 offers to consumer x, 0 ≤ x ≤ \(\frac{1}{2}\), targeted advertising \(a_{1} \left( x \right)~\) at a targeted price \(p_{1} \left( x \right)\), with the understanding that in stage 2 firm 2 can try to poach that consumer by offering \(a_{2} \left( x \right),p_{2} \left( x \right)\). For firm 2’s offer in stage 2 to be attractive to the consumer: \(a_{2} \left( x \right)\) \(= p_{2} \left( x \right) - p_{1} \left( x \right) + a_{1} \left( x \right) + t\left( {1 - 2x} \right)\); and for that offer to be profitable for the firm:\(p_{2} \left( x \right) - [a_{2} \left( x \right)]^{2} \ge 0.\)
Suppose that firm 2 tries to poach consumer x by offering targeted advertising, \(\hat{a}_{2} \left( x \right)~\) at the lowest feasible price \(~\hat{p}_{2} \left( x \right) = \left( {\hat{a}_{2} \left( x \right)} \right)^{2}\). The surplus that consumer x receives from this offer is: \(V - t\left( {1 - 2x} \right) - \hat{p}_{2} \left( x \right) + \hat{a}_{2} \left( x \right).\) Maximizing this surplus with respect to the constraint \(\hat{p}_{2} \left( x \right) = \left( {\hat{a}_{2} \left( x \right)} \right)^{2}\) yields the offer: \(a_{2}^{*} \left( x \right) = \frac{1}{2}\) and \(\hat{p}_{2} \left( x \right) = \frac{1}{4}.~\) This is the best offer that firm 2 can make to any consumer x, 0 < x < \(\frac{1}{2}\), and it yields to consumer x a surplus \(V - t\left( {1 - x} \right) + \frac{1}{4}~\).
To retain consumer x in stage 3, firm 1 must offer in stage 1 a price p1(x) and advertising value \(a_{1} \left( x \right)\) that beats the best offer that its rival could make in stage 2. This means that the offer must be such that \(V - tx - p_{1} \left( x \right) + a_{1} \left( x \right) = ~V - t\left( {1 - x} \right) + \frac{1}{4}\), or that \(p_{1} \left( x \right) = a_{1} \left( x \right) + t\left( {1 - 2x} \right) - \frac{1}{4}.\) Firm 1 wants to maximize the profit of serving consumer x, and choose \(p_{1} \left( x \right)\) and \(a_{1} \left( x \right)\) to maximize \(p_{1} \left( x \right) - \left( {a_{1} \left( x \right)} \right)^{2}\) subject to the constraint that \(p_{1} \left( x \right) = a_{1} \left( x \right) + t\left( {1 - 2x} \right) - \frac{1}{4}.\) This yields the optimal strategy: \(a_{1}^{*} \left( x \right) = \frac{1}{2}~\) and \(p_{1}^{*} \left( x \right) = \frac{1}{4} + t\left( {1 - x} \right)\).
By analogous reasoning firm 2 has to preclude firm 1 from any stage-2 poaching of its consumers in the \(\frac{1}{2} < x \le 1~\) rangeFootnote 17. This implies in stage 1 that firm 2 offers: \(a_{2}^{*} \left( x \right) = \frac{1}{2}\) at \(p_{2}^{*} \left( x \right) =\) \(t\left( {2x - 1} \right) + \frac{1}{4}\) to each consumer x in the \(\frac{1}{2} \le x \le 1\), and thereby preclude firm 1 from making any effort to poach these consumers in stage 2.
As neither firm can in stage 2 target advertising to win consumers whose preferred product version lies closer to its rival’s brand, neither engages in such costly advertising efforts. In stage 2 firm 2 offers consumer x, \(0 \le x \le \frac{1}{2},~\) its product at the marginal cost price of \(p_{2} \left( x \right) = 0.\) Similarly, firm 1 targets no complementary advertising to consumer x, \(\frac{1}{2} \le x \le 1\), and offers these consumers its product at price \(p_{1} \left( x \right) = 0\).
Proposition 2
Below describes more formally the equilibrium advertising and price strategies when firms can send both targeted advertising and targeted prices to consumers, with the recognition that rivals can try to poach each other’s consumers before transactions take placeFootnote 18:
Proposition 2
For V > t > 0:
S1: Firm 1 offers consumer x, 0 ≤ x < \(\frac{1}{2},\) \(a_{1}^{*} \left( x \right) = \frac{1}{2}\) at \(p_{1}^{*} \left( x \right) = \frac{1}{4} + t\left( {1 - 2x} \right)\).
Firm 2 offers consumer x, \(\frac{1}{2}\) < x < 1, \(a_{2}^{*} \left( x \right) = \frac{1}{2}\) at \(p_{2}^{*} \left( x \right) = \frac{1}{4} + t\left( {2x - 1} \right)\).
S2: Firm 1 offers consumer x, \(\frac{1}{2}~\) < x ≤ \(1\) \(a_{1}^{*} \left( x \right) = 0\) at \(p_{1}^{*} \left( x \right)\) = 0.
Firm 2 offers consumer x, 0 ≤ x < \(\frac{1}{2}\), \(a_{2}^{*} \left( x \right) = 0\) at \(p_{2}^{*} \left( x \right)\) = 0.
S: Consumer x, 0 ≤ x < \(\frac{1}{2},\) purchases brand 1; consumer x, \(\frac{1}{2}~\) < x ≤ \(1\), purchases brand 2.
Consumer x = \(\frac{1}{2}\) buys with equal probability brand 1 or 2.
Observe that while firms can differentiate the advertising value that is offered to each consumer, the firms in fact choose to offer the same amount of value to each consumer who is served in stage 3. This is not the case under uniform pricing. This suggests that when consumers value advertising as a complement to the product, price discrimination and targeted advertising are substitute strategies, and firms will favor the former.
There are two ways to understand this result: One is simply to recognize that while it is costless for a firm to change its price, it incurs real costs in creating and targeting value-enhancing advertising that provides real value to any consumer. Firms favor the tool that is least costly to use and so favor price discrimination.
The somewhat deeper intuition is that in our model, the maximum surplus that a firm can provide to consumer x occurs when the firm offers advertising \(a_{i}^{*} = \frac{1}{2}\), at a price that just covers the cost: \(p_{i}^{*} = \frac{1}{4}\). It is the rival’s potential offer of this strategy in stage 2 that each firm must preempt in stage 1 in order to keep its “nearest” consumers. This preemption is most profitably achieved by matching the rival’s potential advertising offer of \(a_{i}^{*} = \frac{1}{2}\) but it can do so at a price that is greater than \(\frac{1}{4}\). Each firm’s locational advantage permits it to earn some markup while still precluding the rival’s threat of poaching in stage 2.
The foregoing logic also explains the outcome when t = 0 and the two products are perfect substitutes. In that case no markup is possible. Competition forces each firm to offer the surplus-maximizing combination of \(a^{*} = \frac{1}{2}\) and \(p^{*} = \frac{1}{4}\) to all consumers. Of course, in this case, each firm earns zero operating profit.
Observe that those consumers with the most intense locational preference for either good consumer x = 0 and x = 1 each pay the highest price \(p^{*} = \frac{1}{4} + t\) whereas the consumer with the weakest preference for either good at x = \(\frac{1}{2}\) pays the lowest price: \(p^{*} = \frac{1}{4}\). The average price across all consumers under discriminatory pricing is \(\bar{p} = \frac{1}{4} + \frac{t}{2}\). Note that this is less than the average price that is paid under uniform pricing and targeted advertising: see Propositions 1(a) and 1(b).Footnote 19
Our benchmark for Proposition 2 is the Thisse and Vives (1988) model in which firms can price discriminate but do not engage in targeted advertising. There, the average equilibrium price is equal to \(\frac{t}{2}\). Producer surplus is \(\frac{{Ht}}{2} - F\); consumer surplus is \(H\left[ {V - \frac{{3t}}{4}} \right]\). Total surplus is \(H\left[ {V - \frac{t}{4}} \right]\).
The average price when firms can discriminate in both pricing and advertising is higher than the average price \(\bar{p} = \frac{t}{2}\) in the benchmark case. Nevertheless, consumer surplus is on average higher with value-enhancing advertising. This is because the higher average price paid is more than offset by the additional value of advertising \(a^{*} = \frac{1}{2}\) that is received.
Proposition 2 implies that consumer surplus is \(CS^{2} = H\left( {V - \frac{3}{4}t + \frac{1}{4}} \right).~~\) Consumers value the advertising that firms offer; and when the firms can price discriminate across consumers, they offer relatively high targeted advertising value to each consumer at more competitive prices. There is, of course, greater price dispersion across consumers when firms can price discriminate.
The profit of each firm is \(\pi ^{2} \left( t \right) = H\frac{t}{4} - F\). This is the same profit as is earned in the Thisse and Vives (1988) benchmark model; hence, producer surplus is the same in each as well.Footnote 20 The reason should be clear: In the absence of targeted advertising, the average price to consumers is \(\frac{t}{2}\). When firms offer targeted value-enhancing advertising, the average price rises to \(\frac{t}{2} + \frac{1}{4}\). The additional \(\frac{1}{4}\) is just enough to cover the cost of the average amount of such advertising.
Note as well that when firms engage in discriminatory pricing and targeted advertising [Proposition 2] the profit that is earned is less than the profit that is earned when firms set uniform prices and engage in targeted advertising [Proposition 1(a), (b)]: \(\pi ^{2} > \pi ^{{1\left( a \right)}}\), and \(\pi ^{2} > \pi ^{{1\left( b \right)}}\). Price discrimination intensifies competition.
Value-enhancing targeted advertising always benefits consumers whether firms can price discriminate or not. It does not always benefit firms: because advertising is costly; and the costs are sunk. That cost is partly why the firms rely more heavily on price discrimination when customization of both prices and advertising are feasible. Under uniform pricing, firms compete less heavily in price and more heavily in targeted advertising.
When firms can price discriminate and target value-enhancing advertising, they nonetheless offer the same advertising value to each consumer in equilibrium. This suggests that the same outcome would be achieved when firms are constrained to offer uniform advertising but are free to discriminate in price. Hence, we do not consider that case here.
Instead, we turn to the final case: Firms are constrained to offer uniform advertising and uniform pricing to all consumers served. This final case captures in a rough way how firms competed before modern digital technology enabled both price discrimination and targeted value-enhancing advertising.
It is straightforward to show that in this case each firm offers \(a^{*} = \frac{1}{2}\) to each consumer served at a price \(p^{*} = \frac{1}{4} + t\).Footnote 21 Firms earn the same profit \(\pi ^{0} = H\frac{t}{2} - F\) as in the standard Hotelling (1929) duopoly case. Consumer surplus is \(CS^{0} = H\left( {V - \frac{5}{4}t + \frac{1}{4}} \right)\). This is higher than in the standard Hotelling (1929) case, but is less than what is possible either when the firms can discriminate in targeted advertising under uniform pricing. It is also less than when the firms can discriminate both in pricing and in advertising. Table 1 summarizes the producer, consumer, and total surplus (excluding fixed cost F) for each case that we have considered.
4 Summary and Conclusions
Much research in economics has focused on how “big data” in the digital age can facilitate price discrimination. Targeted advertising in that context is viewed as firms’ sending differential price and product information to different consumers. The information in the targeted advertising does not directly affect the consumer’s utility from consuming the good. Rather the differential information in the advertising allows a consumer’s notional demand for a product to be realized as effective demand.
However, even before the era of “big data”, advertising was not necessarily informative. Firms can use advertising to enhance the consumption value of the advertised good. What the digital age does is permit firms to version such value-enhancing advertising to different market segments. We investigate the competitive impact of targeted advertising that can directly affect consumer utility.
We adopt a spatial duopoly model in which it may be possible for firms to tailor either their advertising or their pricing, or both, to different consumer types. Firms have a locational advantage in how their product is differentiated and this advantage allows us to rank-order consumers who have locational preferences for the physical attributes of each firm’s good. Targeted value-enhancing advertising affects consumers’ preferences. Such targeted advertising does raise prices, but it does not soften competition. This is because a rival can poach a firm’s consumers not only by reducing prices but also by offering them value-enhancing advertising.
When firms are constrained to set a uniform price, they compete more in targeted advertising. Value-enhancing advertising always benefits consumers, but it is costly. Profits are lower than in the standard uniform-pricing case with no targeted advertising. When firms can practice price discrimination as well as target their advertising, profitability is the same as when they can only price discriminate. Somewhat surprisingly, advertising in this case is not differentiated across consumers. Instead firms choose to compete more directly through prices. Prices are lower, so consumers are better off; and firms are no worse off than if they discriminated in price alone and offered no targeted advertising. From a policy perspective this is the first-best option.
Some may fear that a laissez-faire policy that permits firms to discriminate in both pricing and advertising will lead to excessive advertising – especially advertising that is directed at the consumers that are the most easily attracted by advertising. In our model, such excessive or inefficient advertising is only possible when consumers have very strong brand preferences \(\left( {t > \frac{9}{4}} \right)\) and firms are required to charge all consumers the same price. Even in this case, however, permitting versioned or targeted complementary advertising benefits consumers (but the overall use of resources is inefficiently greater than the additional benefits to consumers).
Our results suggest that price discrimination substitutes for targeted advertising. When allowed to do both, firms discriminate more intensely in their pricing and do not engage in targeted advertising. Our results also support Sutton’s (1991) conjecture that endogenous advertising can intensify competition and thereby provide a greater incentive for firms to exploit scale economies. This would increase market concentration as Sutton (1991) hypothesized.
We have not considered here whether firms are the most efficient providers of the additional advertising value to consumers; say for example when the value enhancement is a donation to philanthropic or environmental causes. However, firms are the entities that have the incentive to acquire information with respect to consumer preferences and to compete with this kind of advertising for customer patronage.
We have also not considered the case in which consumer locational preferences are so strong that the full market is not served. It is easy to speculate though that in this case firms have more market power and this will lead to higher prices and less value-enhancing advertising.
Notes
We focus on value-enhancing advertising as a complement. However, our model could be adapted to firms that offer customized complementary services or products, more generally: e.g., a kitchen contractor that offers a customer a customized paint choice, or an auto dealer that offers a customized complementary service.
Fudenberg and Villas-Boas (2007) provide a nice survey of many of these analyses. See also Taylor and Wagman (2014) who explore price discrimination under different forms of imperfect competition. Of course, Nelson’s (1970, 1974) well-known quality signaling model suggests an alternative mechanism for advertising to be informative. See also Fudenberg and Tirole (2000).
See also Valentino-DeVries, Singer-Vine, and Soltani (2012) on evidence of internet price discrimination.
Anderson and Renault (2006) explore a different explanation for limited information advertising that is rooted in a hold-up problem that shoppers face. This argument seems less applicable to well-known brands such as Coke or Dos Equis.
Barrage, Chyn, and Hastings (2020) find that BP’s “Beyond Petroleum” green advertising campaign significantly mitigated the negative demand response to BP gasoline in the wake of the Deepwater Horizon oil spill. While they interpret this effect as evidence of persuasive advertising, it is also consistent with advertising as a complement.
It is possible that consumers get a benefit from the targeted advertising even if they don’t buy the product that is advertised but do buy other products that the firms sells. Politically, such advertising could lead consumers as voters to prefer candidates whose policies favor the firm that is doing the targeted advertising.
The analysis of Bleier and Eisenbeiss (2015) is somewhat related to ours in that they find that banner ads that are shown to consumers who recently visited a website but did not make a purchase are more effective when the ad is personalized in terms of the time since the visit was made and the context of sites in which the banner is shown. See also Aaker (1991,) on the role of capturing customer attention in effective brand-building advertising.
\(V\ge \frac{3}{2}t\) is necessary to ensure the market is covered in the Hotelling (1929) model. Consumer purchase decisions are randomly distributed over the products if there is a tie. This occurs for a zero-measure set of consumers in equilibrium. See Doraszelski and Markovich (2007) for a similar modeling of advertising effects.
As will be shown below, our analysis also implicitly describes a fourth case in which firms must offer more the same price and advertising package to each consumer.
At these prices there is no profitable deviation for firm 2 to poach in (0,\(\widehat{x})\) or for firm 1 to poach in [\((1-\widehat{\mathrm{x}})\), 1].
The assumption that \(V > \frac{3}{2}t\) holds in all cases so as to ensure that the market is covered.
Ulph and Vulkan, (2001) find that stronger consumer tastes for variety intensify the use of discriminatory prices.
Recall that we have normalized the unit cost of production at c = 0, so this is the marginal cost price.
Unlike the uniform pricing case, the discriminatory pricing case does not vary as the taste parameter t lies below or above 1. Discriminatory pricing permits the firm’s price to increase and cover its advertising cost to any one consumer even if that cost is high. Uniform pricing blocks such adjustment as it implies that increasing the price to one means increasing it to all.
This outcome, like that of Thisse and Vives (1988), reflects the fact that price discrimination permits a firm to poach a rival’s customer with a selective price cut that does not have to be extended to all buyers. This encourages selective price-cutting by both firms. Price competition intensifies as each customer becomes an independent battlefield. See also Norman and Thisse (1996).
For a rival firm to deviate from this strategy it would have to offer each of its consumers and its rivals’ consumers a package \(\stackrel{\sim }{p},\stackrel{\sim }{a}\) that wins their patronage and yields a profit that is greater than \(t/2\). No such deviation is profitable.
References
Aaker, D. A. (1991). Managing Brand Equity. The Free Press.
Acquisti, A., & Varian, H. (2005). Conditioning prices on purchase history. Management Science, 24(3), 367–381.
Anderson, S., & Renault, R. (2006). Advertising content. American Economics Review, 96(1), 93–113.
Barrage, L., Chyn, E., & Hastings, J. (2020). Advertising and environmental stewardship: evidence from the BP oil spill. American Economic Journal: Economic Policy., 12(1), 33–61.
Becker, G., & Murphy, K. (1993). A simple theory of advertising as a good or bad. Quarterly Journal of Economics, 108(4), 941–964.
Bleier, A., & Eisenbeiss, M. (2015). Personalized online advertising effectiveness: The interplay of what, when, and where. Marketing Science, 34(5), 669–688.
Chen, Y. and G. Iyer. (2002). Consumer addressability and customized pricing. Marketing Science, 21(2).
Chen, Y., & Zhang, Z. J. (2009). Dynamic targeted pricing with strategic consumers. International Journal of Industrial Organization, 27(1), 43–50.
Doraszelski, U., & Markovich, S. (2007). Advertising dynamics and competitive advantage. Rand Journal of Economics., 38(3), 557–92.
Esteban, L., Gil, A., & Hernàndez, J. M. (2003). Informative advertising and optimal targeting in a monopoly. Journal of Industrial Economics, 49(2), 161–180.
Esteves, R. B. (2009). Customer poaching and advertising. Journal of Industrial Economics., 57(1), 112–146.
Esteves, R. B., & Resende, J. (2016). Competitive targeted advertising with price discrimination. Marketing Science, 35(4), 576–587.
Fudenberg, D. M., & Tirole, J. (2000). Customer poaching and brand switching. RAND Journal of Economics, 31(4), 634–657.
Fudenberg, D., & Villas-Boas, J. M. (2007). Behavior-based price discrimination and customer recognition. Handbook on economics and information systems, Vol. 1, (pp. 377–433). Emerald Publishing Limited.
Hotelling, H. (1929). Stability in competition. Economic Journal, 39(153), 41–57.
Iyer, G., Soberman, D., & Villas-Boas, J. M. (2005). The targeting of advertising. Marketing Science, 24(3), 461–476.
Jing, B. (2011). Pricing experience goods: the effects of customer recognition and commitment. Journal of Economics and Management Strategy, 20(2), 451–473.
Lambrecht, A., & Tucker, C. (2013). When does retargeting work? Information specificity in online advertising. Journal of Marketing Research, 50(5), 561–76.
Lee, D., Hosanager, K., & Nair, H. (2018). Advertising content and consumer engagement on social media: evidence from facebook. Management Science, 64(11), 5105–5131.
Mikians, J. L., Gyarmati, V. Erramilli, & N. Laoutaris. 2013. Crowd-assisted search for price discrimination in e-commerce: First results. In Proceedings of the 9th ACM conference on emerging networking experiments and technologies (pp. 1–6). Emerald Publishing Limited.
Nelson, P. (1970). Information and consumer behavior. Journal of Political Economy, 78(2), 311–329.
Nelson, P. (1974). Advertising as information. Journal of Political Economy, 82(4), 729–754.
Norman, G., & Thisse, J.-F. (1996). Product variety and welfare under tough and soft pricing regimes. Economic Journal, 106(434), 76–91.
Sahni, N., Narayanan, S., & Kalyanam, K. (2019). An experimental investigation of the effects of retargeted advertising: the role of frequency and timing. Journal of Marketing Research, 56(3), 401–418.
Sutton, J. (1991). Sunk costs and market structure: price competition, advertising, and the evolution of concentration. MIT Press.
Taylor, C. R. (2004). Consumer privacy and the market for customer information. Rand Journal of Economics, 35(4), 631–650.
Taylor, C. R., & Wagman, L. (2014). Consumer privacy in oligopolistic markets: winners, losers, and welfare”. International Journal of Industrial Organization, 34(May), 80–84.
Thisse, J.-F., & Vives, X. (1988). On the strategic choice of spatial price policy. American Economic Review, 78(1), 122–137.
Tuchman, A., Nair, H., & Gardete, P. M. (2018). Complementarities in consumption and the consumer demand for advertising. Quantitative Marketing and Economics., 16(2), 111–174.
Ulph, D., and N. Vulkan, N. (2001). E-Commerce, Mass Customization and Price Discrimination. Working paper. (http://www.worc.ox.ac.uk/fellows/vulkan/ulph-vulkan2.pdf).
Valentino-DeVries, J., J. Singer-Vine, and A. Soltani. (2012). “Websites Vary Prices, Deals Based on Users' Information." Wall Street Journal. 24 December, p.1.
Villas-Boas, J. M. (1999). Dynamic competition with customer recognition. RAND Journal of Economics, 30(Winter), 605–631.
Acknowledgements
We thank Christos Genakos, Michael Pollitt, Jochen Runde, Chris Schneider, Silke Forbes, and George Norman along with the editor of this journal and two anonymous referees for helpful comments. We also thank the Institute for New Economic Thinking (INET) at Cambridge University for its generous support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pepall, L., Richards, D. Targeted Value-Enhancing Advertising and Price Competition. Rev Ind Organ 59, 443–459 (2021). https://doi.org/10.1007/s11151-021-09818-x
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11151-021-09818-x