Abstract
Cartel cases may involve recurrent collusion, with cartel periods interspersed by periods of greater competition. An empirical model of recurrent collusion must account for different data generating processes during collusive and non-collusive episodes and allow for the dating of such episodes. It should also allow for the possibility of flexible transitions between collusive and non-collusive episodes. This paper proposes a Markov regime-switching model to detect recurrent periods of collusive damages and to estimate cartel effectiveness in any given time period. We use this information to estimate overcharges, which we show are much higher than those suggested by conventional approaches.




Similar content being viewed by others
Notes
Throughout this paper we focus on cement, the binding substance used in construction, and not concrete, which is a composite material consisting of cement and other building aggregates.
See also Kandori (1991), who finds similar results for alternative specifications of the correlation structure of demand shocks.
The overcharge literature typically relies on static OLS models. OLS models provide asymptotically consistent estimators only in the presence of cointegration among the dependent variables, which are often unit root processes. Additionally, the autoregressive distributed lag (ARDL) form is preferable, since it provides a better representation of the dynamic effects, see (Boshoff 2015, 228) for discussion.
We first verified that the optimal number of regimes, consistent with the data, is two. The results are reported in “Appendix 2”.
Cement prices is a unit root process. Therefore, there is strong first order persistence and the Markov assumption is appropriate.
Note that this is a single equation framework. A multiple equation framework was also estimated and the results indicated that there is no simultaneity. The results are available upon request.
The main inputs in South African cement production are limestone and lime, coal, shale, silica sand, and gypsum (Lafarge 2018; AfriSam 2016). Limestone constitutes two-thirds of the raw materials used in South African cement manufacturing (Leach 1994). Roughly one and a half tonnes of limestone is required to produce one tonne of cement (Ali 2013).
One interesting three-regime model—for the purposes of studying recurrent collusion in the cement market – would be one whose three regimes can be identified respectively as a legal collusion regime, an illegal collusion regime, and a non-collusive regime. Alternatively, another interesting model would be one whose three regimes can be identified respectively as a collusion regime, a competitive regime (before episodes before 2011) and another competitive regime (post-2011, to signal greater competition). The data clearly support only a two-regime model, which indicate that all collusive episodes are generated by the same regime. Similarly, all non-collusive episodes are generated by the same regime.
References
Abrantes-Metz, R. M., & Bajari, P. (2010). A symposium on cartel sanctions: screens for conspiracies and their multiple applications. Competition Policy International, 6, 129–253.
AfriSam (2016). Cement technical reference guide. https://www.afrisam.co.za/media/76326/Cement___Technical_Reference_Guide.pdf. Accessed 19 Jan 2018.
Ali, A. (2013). Lafarge cement value chain. http://www.slideshare.net/linashuja/lafarge-cement-value-chain. Accessed 19 Jan 2018.
Athey, S., Bagwell, K., & Sanchirico, C. (2004). Collusion and price rigidity. The Review of Economic Studies, 71(2), 317–349.
Bagwell, K., & Staiger, R. W. (1997). Collusion over the Business Cycle. The RAND Journal of Economics, 28(1), 82. https://doi.org/10.2307/2555941.
Bai, J., & Perron, P. (2003). Computation and analysis of multiple structural change models. Journal of Applied Econometrics, 18(1), 1–22. https://doi.org/10.1002/jae.659.
Boshoff, W. H. (2015). Illegal cartel overcharges in markets with a legal cartel history: Bitumen prices in South Africa. South African Journal of Economics, 83(2), 220–239. https://doi.org/10.1111/saje.12074.
Boswijk, H. P., Bun, M. J., & Schinkel, M. P. (2017). Cartel dating. Amsterdam centre for law and economics working paper No 2016-05. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2862340. Accessed 19 Jan 2018.
Breunig, R., Najarian, S., & Pagan, A. (2003). Specification testing of Markov switching models. Oxford Bulletin of Economics and Statistics, 65(s1), 703–725.
Club, M. (2007). Media club South Africa. http://www.mediaclubsouthafrica.com/component/content/article?id=93:world. Accessed 19 Jan 2018.
Commission, S. A. C. (2015). Commission refers a case of collusion against Natal Portland Cement Cimpor (Pty) Ltd. http://www.compcom.co.za/wp-content/uploads/2015/01/Commission-refers-a-case-of-collusion-against-Natal-Portland-Cement-Cimpor-Pty-Ltd.pdf. Accessed 19 Jan 2018.
Connor, J. M. (2003). Private international cartels: Effectiveness, welfare, and anti-cartel enforcement. Staff paper 03–12. Department of Agricultural Economics, Purdue University, 5 November 2003.
Connor, J. M. (2014). Price-fixing overcharges: revised (3rd ed.). American Antitrust Institute. http://papers.ssrn.com/sol3/Papers.cfm?abstract_id=2400780. Accessed 19 Jan 2018.
Crede, C. J. (2015). A structural break cartel screen for dating and detecting collusion. https://www.researchgate.net/profile/Carsten_Crede/publication/301637397_A_structural_break_cartel_screen_for_dating_and_detecting_collusion/links/571f525108aefa64889a601a.pdf. Accessed 19 Jan 2018.
Dalkir, S. (2006). Near discoveries and half punishments against cartels can be self-defeating. Ktisat, Letme ve Finans, 21, 5–22.
Davis, P., & Garces, E. (2010). Quantitative techniques for competition and antitrust analysis. Princeton: Princeton University Press.
Fabra, N. (2006). Collusion with capacity constraints over the business cycle. International Journal of Industrial Organization, 24(1), 69–81. https://doi.org/10.1016/j.ijindorg.2005.01.014.
Fourie, F., & Smith, A. (1994). The South African cement cartel: An economic evaluation. South African Journal of Economics, 62(2), 80–93.
Frank, N., & Lademann, R. P. (2010). Economic evidence in private damage claims: What lessons can be learned from the German cement cartel case? Journal of European Competition Law and Practice, 1, 360–366.
Friederiszick, H. W., & Röller, L.-H. (2010). Quantification of harm in damages actions for antitrust infringements: Insights from German cartel cases. Journal of Competition Law and Economics, 6, 595–618.
Goldfeld, S. M., & Quandt, R. E. (1973). A Markov model for switching regressions. Journal of econometrics, 1(1), 3–15.
Govinda, H., Khumalo, J., & Mkhwanazi, S. (2014). On measuring the economic impact: savings to the consumer post cement cartel burst. In: Competition law, economics and policy conference (Vol. 4). URL http://compcom.co.za.www15.cpt4.host-h.net/wp-content/uploads/2014/09/On-measuring-the-economic-impact-savings-to-the-consumer-post-cement-cartel-burst-CC-15-Year-Conference.pdf. Accessed 19 Jan 2018.
Green, E. J., & Porter, R. H. (1984). Noncooperative collusion under imperfect price information. Econometrica, 52(1), 87. https://doi.org/10.2307/1911462.
Haltiwanger, J., & Harrington, J. E. (1991). The impact of cyclical demand movements on collusive behavior. The RAND Journal of Economics, 22(1), 89. https://doi.org/10.2307/2601009.
Hamilton, J. D. (1989). A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica, 57(2), 357. https://doi.org/10.2307/1912559.
Harrington, J. E. (2004). Post-cartel pricing during litigation. The Journal of Industrial Economics, 52(4), 517–533.
Hüschelrath, K., & Veith, T. (2014). Cartel detection in procurement markets. Managerial and Decision Economics, 35(6), 404–422. https://doi.org/10.1002/mde.2631.
Hüschelrath, K., Müller, K., & Veith, T. (2013). Concrete shoes for competition: The effect of the german cement cartel on market price. Journal of Competition Law and Economics, 9(1), 97–123. https://doi.org/10.1093/joclec/nhs036.
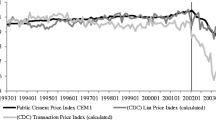
Hüschelrath, K., Müller, K., & Veith, T. (2016). Estimating damages from price-fixing: The value of transaction data. European Journal of Law and Economics, 41(3), 509–535. https://doi.org/10.1007/s10657-013-9407-y.
Kandori, M. (1991). Correlated demand shocks and price wars during booms. The Review of Economic Studies, 58(1), 171. https://doi.org/10.2307/2298053.
Khimich, A. (2014). Essays in competition policy. http://publications.ut-capitole.fr/16282/. Accessed 19 Jan 2018.
Kim, C.-J. (1994). Dynamic linear models with Markov-switching. Journal of Econometrics, 60(1–2), 1–22.
Lafarge. (2018). All about cement: Manufacturing process. http://www.lafarge.co.za/wps/portal/za/2_2_1-Manufacturing_process. Accessed 19 Jan 2018.
Leach, D. F. (1994). The South African cement cartel: A critique of fourie and smith. South African Journal of Economics, 62(3), 156–168. https://doi.org/10.1111/j.1813-6982.1994.tb01229.x.
Levenstein, M., Marvo, C., & Suslow, V. (2015). Serial collusion in context: Repeat offenses by firm or by industry?. http://www.oecd.org/officialdocuments/publicdisplaydocumentpdf/?cote=DAF/COMP/GF(2015)12&docLanguage=En. Accessed 19 Jan 2018.
Levenstein, M. C., & Suslow, V. Y. (2016). Price? Fixing hits home: An empirical study of US price-fixing conspiracies. Review of Industrial Organization, 48(4), 361–379. https://doi.org/10.1007/s11151-016-9520-5.
Lorenz, C. (2008). Screening markets for cartel detection: Collusive markers in the CFD cartel-audit. European Journal of Law and Economics, 26(2), 213–232.
Maheu, J. M., & McCurdy, T. H. (2000). Identifying bull and bear markets in stock returns. Journal of Business and Economic Statistics, 18(1), 100. https://doi.org/10.2307/1392140.
McCrary, J., & Rubinfeld, D. L. (2014). Measuring benchmark damages in antitrust litigation. Journal of Econometric Methods., 3(1), 63–74. https://doi.org/10.1515/jem-2013-0006.
Rotemberg, J., & Saloner, G. (1986). A supergame-theoretic model of price wars during booms. The American economic review, 76(3), 390–407.
Salvo, A. (2010). Inferring market power under the threat of entry: The case of the Brazilian cement industry. The RAND Journal of Economics, 41(2), 326–350.
Smith, D. R. (2008). Evaluating specification tests for markov-switching time-series models. Journal of Time Series Analysis, 29(4), 629–652. https://doi.org/10.1111/j.1467-9892.2008.00575.x.
UNCTAD. (2005). A synthesis of recent cartel investigations that are publicly available (TD/RBP/CONF.6/4).
Utton, M. A. (2011). Cartels and economic collusion: The persistence of corporate conspiracies. Cheltenham: Edward Elgar Publishing.
White, H., Marshall, R., & Kennedy, P. (2006). The measurement of economic damages in antitrust civil litigation. ABA Antitrust Section Economic Committee Newsletter, 6, 17–22.
World Bank. (2016). South Africa economic update: Promoting faster growth and poverty alleviation through competition. http://documents.worldbank.org/curated/en/917591468185330593/pdf/103057-WP-P148373-Box394849B-PUBLIC-SAEU8-for-web-0129e.pdf. Accessed 5 June 2018.
Acknowledgements
We are grateful for the useful comments by the participants and discussants at the BECCLE 2017 and CRESSE 2017 conferences. The paper also benefited from discussion at Stellenbosch University and the University of Cape Town. We thank Joe Harrington, John Connor, Johannes Paha, Maarten Pieter Schinkel, and Maurice Bun for comments on earlier versions.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Methodology–Filter and Smoothing
We start with the conditional log likelihood function of Eq. (5) given by:
where \({{\Omega }}_t=\{p_t,\ p_{t-1},\ldots , p_1,p_0,{\varvec{x}}_t,{\varvec{x}}_{t-1},\ldots ,{\varvec{x}}_0\}\) denote the collection of all the observed variables up to time t, and \(\varvec{\theta }\varvec{=}{(\sigma ,\ a_1,\ldots ,a_4,\ {\gamma }_1,\ldots ,{\gamma }_4,\ c_0,\ \omega ,\ p_{11},p_{22})}^{'}\) is a vector of population parameters. Maximum likelihood estimation (MLE) of Eq. 5 requires construction of the conditional density function \(f(p_t\,|\,{{\Omega }}_{t-1};\,\varvec{\theta })\).
Following Hamilton (1989), we construct the conditional densities recursively as follows: Suppose that \(P(S_{t-1}=j{{\Omega }}_{\mathrm {t-1}};\ \varvec{\theta }\varvec{)}\) is known. Given the state variable \(S_t=j\) and the previous observations the conditional probability density function is given as:
To construct \(f(p_t\,|\,{{\Omega }}_{t-1};\,\varvec{\theta })\) Hamilton use the following equations
Since \(p_{ij}\) is known and \(P(S_{t-1}=j\,|\,{{\Omega }}_{t-1};\varvec{\theta })\) is assumed as given we have \({\xi }_{i,t-1}\). Now to derive \(f(p_t\,|\,{{\Omega }}_{t-1};\ \varvec{\theta })\) we use
Substituting (7) into (8) and re-arranging we have
Now that we have \(f(p_t\,|\,{{\Omega }}_{t-1};\varvec{\theta })\), the next step is to update (7) so that we can calculate \(f(p_{t+1}\,|\,{{\Omega }}_t;\varvec{\theta })\) where
The conditional density function \(f(p_{t+1}\,|\,S_t=i,\ {{\Omega }}_t;\ \varvec{\theta })\) will have the same form as in Eq. (6). Therefore, the only requirement to calculate (10) is \({\xi }_{i,t}=P(S_t=i\,|\,{{\Omega }}_t;\varvec{\theta })\). This is calculated by simply updating \({\xi }_{i,t-1}\) to reflect the information contained in \(p_t\). The update is performed using a Bayes’ rule:
Therefore, \(f(y_t\,|\,{{\Omega }}_{t-1};\varvec{\theta })\) is obtained for \(t=1,\ 2,\ldots , T\) by assigning a starting value \(P(S_{t-1}=j{{\Omega }}_{\mathrm {t-1}};\ \varvec{\theta }\varvec{)}\) to initialize the filter and then to iterate Eq. (7)–(11).
The question that remains is how to set \(P(S_{t-1}=j\,|\,{{\Omega }}_{\mathrm {t-1}};\ \varvec{\theta })\) to initialize the iterations for the filter? When \(S_t\) is an ergodic Markov chain, the standard procedure is to simply set \(P(S_{t-1}=j\,|\,{{\Omega }}_{\mathrm {t-1}};\ \varvec{\theta })\) equal to the unconditional probability \(P(S_0=i)\). The unconditional probabilities is given by
An advantage of the Hamilton filter is that it directly evaluates \(P(S_t=i\,|\,{{\Omega }}_t;\varvec{\theta })\), which is referred to as the “filtered” probability. The estimates of \(P(S_t=i\,|\,{{\Omega }}_t;\varvec{\theta })\) can further be improved by “smoothing”. This is done by using the information set in the final period \({{\Omega }}_T\), in contrast to the filtered estimates that only use the contemporaneous information set \({{\Omega }}_{\mathrm {t}}\). The likelihood of the observed data’s appearing in different periods is linked together by the transition probabilities.
Therefore, the likelihood of being, for example, in regime i in period t is improved by using information about the future realisations of \(p_d\), where \(d>t\). A suitable smoothing technique is provided by Kim (1994). The smoothing method requires only a single backward recursion through the data. Kim (1994) shows that the joint probability under the Markov assumption is given by
To move from (14) to (15), it is important to note that under the correct assumptions, if \(S_{t+1}\) is known, the future data in (\({{\Omega }}_{t+1},\ldots , {{\Omega }}_T)\) will contain no additional information about \(S_t\). Therefore, by marginalizing the joint probability with respect to \(S_{t+1}\), the smoothed probability in period t is obtained by
Appendix 2: Motivation and Choice of Markov RS Model
Consider a standard ARDL model of price with the following form:
with \({\varepsilon }_t\ \sim \ N\left( 0,{\sigma }^2\right) \), where \(p_t\) denotes price at time t, and \({\varvec{x}}_t\) denotes a vector of demand and costs drivers as shown in Table 3 The residual diagnostics are reported in Table 7.
The residuals of the ARDL model (Eq. 17) exhibit heteroskedasticity and serial correlation. Such a result is to be expected in the presence of regime changes, since the residuals will no longer be Gaussian. From the diagnostic tests it is evident that the linear functional form of Eq. 17 is unsuitable. This result could be anticipated, given the prior knowledge of the cement cartel and cement price regime shifts. Therefore, standard least-squares estimation of (17), including a dummy variable to capture overcharges, will not give an accurate measure of the true overcharge.
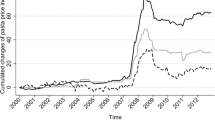
In some specifications the coefficient of the electricity variable had the incorrect sign. Specifically it was found that there is a negative relationship between electricity prices and the price of cement, which is not a sensible conclusion. A graphical investigation of Fig. 5 provides some insight as to why this was the case.
There appear to be time periods for which there is positive correlation and time periods for which there is negative correlation. It is therefore sensible to make the coefficient of electricity regime-dependent. The results confirm this idea, where the coefficient for electricity is positive in the collusive regime \((S_t=1)\) and effectively zero in the non-collusive regime \((S_t=1)\).
Appendix 3: Diagnostic Tests
This section reports the diagnostic tests for both the Markov RS model, (that generated the transition probabilities for the two regimes) and the final ARDL model that was used to calculate the overcharge. Diagnostic tests for the ARDL model are reported in Table 8. As shown, the ARDL model passes the standard diagnostic tests.
The ARDL model relies on the cartel effectiveness measure, which is calculated from the RS model. Performing diagnostic tests for an RS model is more complex than in standard linear models and, until recently, the applied literature has often relied on only a few (if any) of these tests (Breunig et al. 2003; Smith 2008).
A challenge that is faced when performing diagnostic tests for an RS model is that the true residuals are unobserved, as they are dependent on the unobserved state variable. To overcome this issue, we follow the methodology proposed in Maheu and McCurdy (2000), according to which expected residual are calculated, conditioned on past information. Smoothed values obtained from the Kim filter cannot be used to construct the residuals, as the filter includes future information and, as a result, the current residual will contain future information.
Table 9 reports selected diagnostic tests for the RS model, which we are capable of generating. These appear satisfactory. Normality tests on residuals in an RS model are more complicated and the RS model performs less well on our version of these tests. While deviation from normality may be problematic for inference, this is not the main focus of our paper. Therefore, in sum, we are confident of the stability of the model.
Appendix 4: Comparison to Structural Breaks
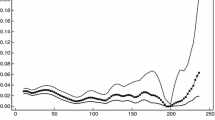
As discussed tests for structural breaks face limitations in this example. The recursive residuals (Fig. 6) cross the significance band at various time points and do not give a clear indication for how long these possible breaks affected the price series. While the CUSUM test (Fig. 7) provides a better picture, the result is not as convincing as the probabilities of Fig. 1. The test indicates a break in the model from 2001 to around 2007. These dates do not accurately depict our prior knowledge of the cement case, since it would suggest that damages were only observed three years after the cartel was formed and ceased two years before the information exchange was terminated.
The Bai–Perron test in Table 10 treats the break dates as unknown and estimates them along with the regression coefficients with the use of least-squares estimation. The break points are estimated as 1996Q2, 2005Q2 and 2009Q2. This is certainly a more accurate depiction of the changes in the d.g.p. compared to the recursive residuals and squared CUSUM. However, as expected the test takes 1996Q2 as the first break date. Therefore, construction of a dummy variable that is based on this test will include the price war during this time as part of the collusive regime and lead to a lower overcharge estimation.
Rights and permissions
About this article
Cite this article
Boshoff, W.H., van Jaarsveld, R. Recurrent Collusion: Cartel Episodes and Overcharges in the South African Cement Market. Rev Ind Organ 54, 353–380 (2019). https://doi.org/10.1007/s11151-018-9637-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11151-018-9637-9