Abstract
We compare the wholesale model and the agency model that characterise a vertical relation in a bilateral duopoly framework. Results suggest that the agency model may be regarded as an example of retailer power resale price maintenance and provide an economic view of why restraints of this kind should be evaluated under the rule of reason. While competition is more likely to be undercut under the agency model, relative to the wholesale model, the agency model benefits consumers by offering relatively lower retail prices and greater demand.
Similar content being viewed by others
1 Introduction
Today individuals shop at high street stores, supermarkets, as well as a variety of online retailers: Goods often pass through more elaborate supply and distribution chains. The manufacturer-retailer contracts that link the vertical relations, not surprisingly, are not always identical.
Among the various vertical contracts observed in practice, this paper deals with two, the wholesale model and the agency model. Under the wholesale model, a manufacturer sets the wholesale price and sells to a retailer, and the retailer sets the retail price and deals with final consumers. Under the agency model, a retailer specifies the revenue sharing rate, before selling to final consumers at the retail price set by a manufacturer. The agency model involves resale price maintenance (RPM) because the retail price that is set by the manufacturer, not the retailer.
While the wholesale model remains common in a bricks-and-mortar environment, the agency model becomes predominant in online markets. Some natural questions to ask then would be why a certain vertical contract is chosen against the others, and which contract is beneficial to consumers. These questions appear more relevant given the (in)famous Apple Footnote 1 case that involved the switch of vertical contracts from the wholesale to the agency model. Plausibly also due to the fact that the agency model has been adopted by several large online retailers—e.g., Amazon marketplace, Apple, eBay, Google and various booking websites—concerns might arise with regard to the nature of such contracts, the powerful position of those retailers, and whether consumers and market performance are benefited or harmed as a consequence.
In fact, Apple was not the first antitrust case in which distinctions between the wholesale and agency models were highlighted. In the 1967 Schwinn Footnote 2 case, which involved the adoption of territorial restraints, the U.S. Supreme Court decided that the per se illegality of vertical restraints applied to the transactions in which Schwinn sold bicycles to distributors for resale to dealers, a wholesale model under which the ownership of bicycles was transferred. But the transactions in which Schwinn sold and shipped directly to dealers and paid distributors a commission for taking the order—an agency distribution under which Schwinn retained the ownership of bicycles—were legal. That is, the same vertical restraints were treated differently under wholesale and agency models, and the judicial reasoning hinged on the legal ownership of property.
If we compare Apple and Schwinn, the antitrust view towards the agency model seems to be somewhat inconsistent. One may argue that it is due to the different contexts in which the vertical restraints are adopted. Apple involved multiple vertical restraints as well as horizontal conspiracy among the publishers, and the agency model was a complementary device to the price fixing clause used. Yet, the Court’s reasoning in Schwinn that “…it is unreasonable without more for a manufacturer to seek to restrict and confine areas or persons with whom an article may be traded after the manufacturer has parted with dominion over it”Footnote 3 was heavily criticized as “it may indicate that such confinement is unlawful absent an acceptable business justification” (1977). In this view, instead of the ownership of property, what should be evaluated is the actual impact of restraints on market performance and how such impacts differ under wholesale and agency models. In 1977, the U.S. Supreme Court reversed the ten-year-old decision of the per se illegality of restraints involved in wholesale distribution in Schwinn by applying the rule of reason in Sylvania Footnote 4 in deciding the legality of non-price restraints.
While the linear price wholesale model is well understood as the basic form of vertical relations in economic theory (Tirole 1988), recent papers that study the agency model tend to focus more on specific issues related to the e-book market, such as the device—e.g., Kindle (Gaudin and White 2014); the MFN clause (Boik and Corts 2016); and consumer lock-in (Johnson 2013)—rather than the systematic analysis of the agency model per se.
In this paper, we seek to examine the agency model and compare it to the wholesale model, which constitutes the basis of understanding some transformations in vertical relations. We do so in a bilateral duopoly framework that was developed by Dobson and Waterson (1996, 2007) which incorporates both interbrand competition (competition between manufacturers) and intrabrand competition (competition between retailers). When making comparisons, we focus on welfare conditions and the relative profitability of the alternative schemes for manufacturers and retailers. We then interpret how the results that are obtained from the comparison are relevant and useful for the understanding of the nature of the agency model, as well as the antitrust treatment of restraints of this kind.
With regard to welfare conditions, we find that in symmetric equilibrium retail prices are always lower under the agency model relative to the wholesale model. The driving force is double marginalisation: It exists under the wholesale model and disappears under the agency model. Consumer surplus is always higher under the agency model, whereas aggregate profits are higher under the wholesale model for a wider range of degrees of product differentiation in the market. Social surplus is higher under the agency model—provided that manufacturers’ goods are sufficiently differentiated. Given these results, if courts were to distinguish between restraints involved in sale and non-sale transactions, as they did in Schwinn, the verdict might be more reasonably based on how the welfare impacts of restraints differ in these two scenarios—the agency model is more beneficial to consumers—instead of the legal ownership of property.
With regard to the relative profitability of the alternative schemes for manufacturers and retailers, we find that manufacturer profits are always higher under the wholesale model, whereas retailer profits are higher under the agency model unless manufacturers’ goods are close substitutes. This result offers two insights: First, although manufacturers, ceteris paribus, have no profit-driven incentive to switch away from the wholesale model, the switch is considerably likely in favour of retailers. The popularity of the agency model in some markets in turn implies the powerful position of retailers in those markets. Second, retailers can benefit from the differentiation at the manufacturer level under the agency model, which contrasts with the inverse association in vertical relations suggested by Steiner (1993) that stronger brands tend to lead to lower retail margins and higher manufacturing margins. Hence manufacturers and retailers’ incentives are better aligned under the agency model.
The economic theory on vertical restraints has been traditionally concerned with manufacturer power restraints imposed by manufacturers to neutralize potential externalities and induce retail service; this assumes that retailers have no market power (e.g., Telser 1960), or some market power (e.g., Mathewson and Winter 1984). When we relate the above result to this strand of the literature, an interesting question arises as to why manufacturers would adopt the agency model. In his re-evaluation of Schwinn, Grimes (2007) tells the story behind the case as “an insecure brand seller imposes downstream power restraints.”Footnote 5 Downstream or retailer power restraints, he further defines, “may be imposed by the upstream seller, but the seller acts in response to conditions of downstream power.” In this view, the agency model may be an example of retailer power RPM, which is adopted by manufacturers who are in need of brand promotion. While such retail power restraints also serve to induce retail service provision, the underlying assumption of the power relation between manufacturers and retailers is different from the traditional view. This might plausibly also have been part of the story in Apple.Footnote 6
Relative to the wholesale model, the higher consumer surplus and better alignment of incentives under the agency model constitute a conflict, which is critical in determining the antitrust status of restraints of this kind: They benefit consumers but undercut competition. The evolution of the antitrust treatment of vertical restraints from per se rules to the rule of reason suggests the scope of applying the rule of reason in treating restraints of this kind. While some retailer power restraints do not meaningfully harm consumers or competition, such as those in Schwinn, some others do. With the alignment of incentives, the agency model is prone to additional and potentially more harmful restraints, such as the MFN clause that was involved in Apple.Footnote 7 Based on our results, we consider the economic analysis of the actual impact of restraints, instead of the ownership of property, to be a better support for applying the rule of reason in treating the agency model.
The paper proceeds as follows: Sect. 2 reviews the related literature. Section 3 presents the framework for our analysis, in which we characterise the vertical relation first by the wholesale model and then by the agency model. Section 4 compares the symmetric equilibrium outcomes under the two models. Section 5 discusses the results. Section 6 concludes.
2 Related Literature
This paper is related to the law and economics literature on vertical restraints. Vertical restraints are imposed by manufacturers to cope with vertical externalities such as double marginalisation, and horizontal externalities such as pre-sale service underprovision due to intrabrand competition (Tirole 1988). Restraints, especially those to neutralize horizontal externalities, often allow retailers to capture some of the industry rents. These rents have been used to provide a procompetitive theory of restraints: Manufacturers may use these rents to entice retailers to provide promotional efforts that are often costly. For example, Marvel and McCafferty (1996) compare the efficiency of using RPM and exclusive territories to combat free-riding. On the other hand, these rents may be used in anticompetitive ways by facilitating collusion and blocking new entrants. For example, Shaffer (1991) compares RPM and slotting allowances and finds that both restraints increase prices and retail profits, and may be seen as practices to facilitate coordination. Asker and Bar-Isaac (2014) suggest that the rents created by restraints for retailers can induce them not to accommodate an entrant to the manufacturer level since entry would reduce those rents.
The above literature suggests that the anticompetitive effects of restraints are mostly likely to arise when they are introduced to dampen intrabrand competition and are not meant to enhance the efficiency of the vertical relation. This may explain why retailer-sponsored “competition-reducing” restraints are almost always considered to increase prices and harm consumers, and thus are presumptively unlawful (Tirole 1988). For example, Dobson and Waterson (2007) examine the effects of RPM in the presence of countervailing power and find that the social effects of RPM are likely to be negative when retailer power is strong.
In this paper, we show that although the agency model is likely to relax competition and increase retailer profits, it is beneficial to consumers and can be socially desirable. We suggest that the agency model is better understood as an example of the retailer power restraints that we mentioned in Sect. 1. A major difference between retailer-sponsored “competition-reducing” restraints and retailer power restraints, as suggested by Grimes (2007), is that retailer power restraints are imposed with genuine business purposes, although intrabrand competition may be reduced as a result. Specifically, strong brands have little incentive to impose restraints that benefit retailers, because retailers that do not promote these brands to increase sales would be worse off. However, weak or insecure manufacturers would have to provide extra incentives to induce retailers to promote their brands, even if it is costly for them to do so. This corresponds to the empirically verified inverse association between the strength of brands and retail margins (Steiner 1993; Lynch 2004).
From both law and economics perspectives, contemporary vertical restraint theory recognises retailing as a distinct stage of vertical relations and that it is a mistake to neglect the role of intrabrand competition in affecting consumers’ choices, as well as the exercise of countervailing power (e.g., Steiner 1991; Dobson and Waterson 1999). The understanding of the agency model as retailer power RPM is meaningful as it helps to distinguish the agency model from being perceived as a form of vertical integration that ignores the changing power relation between manufacturers and retailers.Footnote 8
Among the recent studies that compare different vertical contracts, our characterisation of the agency model follows Foros et al. (2014), but the counterparts that are used for comparison differ in their paper and ours. Their paper compares the agency model to an alternative model in which the revenue sharing rate and the retail price are both set by retailers, whereas our benchmark is the wholesale model. In addition, they focus on the equilibrium contract selection problem of firms and allow different contracts to be used in the same market, whereas we assume common contracts and focus on the different effects of contract forms on competition and welfare.
The comparison between the wholesale and the agency models is also made in Johnson (2017), who studies the effects of MFN clauses based on the comparison. The results with regard to retailer profits and industry profits in his paper are different from ours; the differences arise because of different demand functions that are used and different assumptions on market coverage. While he assumes market coverage to be full, changes in demand are important in our paper.
A further related strand of literature is on markets with intermediaries. Comparisons have been made between the two forms of intermediation: The intermediary buys and resells a product (the wholesale model), or simply refers buyers for a fee (the agency model) (Belleflamme and Peitz 2010). Condorelli et al. (2013) suggest that, when information is asymmetric and the intermediary has privileged information about consumers, efficiency increases when the latter form is used.
3 Model
We consider a market with two manufacturers, j = 1, 2, and two retailers, i = 1, 2. Each manufacturer j produces a single good j, and each retailer i presents final consumers with goods from both manufacturers: \(q_{i}^{j} > 0\), such that vertical contracts are nonexclusive. Correspondingly, consumers are able to choose from four “final goods” and thus make two decisions: which retailer store to shop, and which manufacturer good to buy. This is intuitive as firms in vertically related markets compete not only horizontally with firms at the same level over consumer demand, but also vertically with firms at the other level over their respective shares of retail prices. We assume manufacturer goods and retailer services to be symmetrically differentiated and all production costs to be zero.
Following Dobson and Waterson (Dobson and Waterson 1996, 2007) and Gabrielsen and Johansen (2015), we assume that consumers make decisions to maximise
This utility function gives rise to the downward sloping inverse demand function
The parameter \(\beta \in \left[ {0, 1} \right)\) measures the degree of intrabrand competition between retailers’ services, and the parameter \(\gamma \in \left[ {0, 1} \right)\) measures the degree of interbrand competition between goods.Footnote 9 Retailers’ services are perceived to be wholly differentiated when β = 0 and become closer substitutes as \(\beta \to 1\). Likewise, when \(\gamma = 0\), the two goods are viewed as perfectly differentiated and demand-unrelated; as \(\gamma \to 1\), they become closer substitutes.
We assume that firms behave non-cooperatively. The direct demand function is given by
The quantity that is demanded for good j at retailer \(i\) is a function of: own price, \(p_{i}^{j}\); the prices of two relatively closer substitutes, \(p_{i}^{ - j}\) and \(p_{ - i}^{j}\); and the price of another substitute that is further away in the product space, \(p_{ - i}^{ - j}\). Given the ranges of parameters, it can be easily verified that the own-price effect dominates each cross-price effect.
The above direct demand system has two features that are worth highlighting: First, the cross-price effect between different goods that are sold by different retailers is negative; \(\partial q_{i}^{j} /\partial p_{ - i}^{ - j} = - \beta \gamma /\left( {1 - \beta^{2} } \right)\left( {1 - \gamma^{2} } \right) < 0\), which contrasts with our general brief that as the price of one good increases, the demand for its substitute increases. Gabrielsen and Johansen (2015) suggest that the negative cross-price effect can be explained as a “second-order effect”: As \(p_{ - i}^{ - j}\) increases, consumers would optimally switch away from good (− i, − j) and demand more (i, − j) and \(\left( - i,j \right)\), as these two are relatively closer substitutes for \(\left( { - i, - j} \right)\). However, as more (i, − j) and (− i, j) are consumed, since it is relatively closer substitutes to them, (i, j) would consequently be demanded less. This negative “second-order effect” dominates the direct substitution effect, leading to a negative cross-price effect.
Second, demand is determined by two countervailing effects: A price effect, and a market size effect. For a common price, demand becomes \(\left( {1 - p} \right)/ \left( {1 + \beta } \right)\left( {1 + \gamma } \right)\), which is increasing in degrees of differentiation in the market. This means that high demand may be driven by low prices or by highly differentiated products. Some studies consider vertical restraints that increase demand to be presumptively procompetitive (e.g., Bork 1978); others argue that consumers may “end up with the wrong product at the wrong price” (Grimes 2007). Overall, this demand system allows for differentiation at both levels of the vertically related market to be parameterised in a convenient form, which in turn offers clear and tractable solutions.
We assume that the manufacturers cannot directly reach final consumers. We characterise the vertical relation first under the wholesale model and then under the agency model. We focus on symmetric equilibrium throughout the analysis.
3.1 The Wholesale Model
The timing under the wholesale model is as follow:
-
1.
Manufacturers set wholesale prices simultaneously. The wholesale price set by manufacturer j to retailer i is w j i .
-
2.
Retailers set retail prices simultaneously. The price set by retailer i for good j is p j i .
Retailer \(i\), denoted as \(R_{i}\), faces the following optimisation problem
The corresponding first-order condition is given by
From (4), we get
Solve for the reduced form of the above
Substituting the equilibrium second-stage prices into the direct demand function (2), we get the second-stage quantities demanded
Manufacturer \(j\), denoted as \(S^{j}\), faces
The corresponding first-order condition is given by
From (6), we get
When we impose symmetry, the equilibrium wholesale prices, denoted as \(w^{*}\), are
The symmetric equilibrium retail prices and demand for each of the goods, denoted as \(p^{*}\) and \(q^{*}\) respectively, are given by
p * decreases in β and γ: Higher values of β and γ mean lower degrees of differentiation between goods and services, and thus lower prices. \(q^{* }\) initially decreases and then increases in β and γ. This is because, as we mentioned earlier, demand is decided by two countervailing effects: As β and \(\gamma\) increase, on the one hand, goods and services become less differentiated and demand for the individual goods falls; on the other hand, price decreases and demand increases. Whether demand for the individual goods increases or decreases in β and \(\gamma\) thus depends on which effect is stronger.
We present the complete set of symmetric equilibrium results under the wholesale model, including firms’ profits in the following lemma:
Lemma 1
Under the wholesale model, there exists a symmetric equilibrium in which
-
w * = (1 − γ)/(2 − γ);
-
p * = [(1 − β)(2 − γ) + 1 − γ]/(2 − β)(2 − γ);
-
q * = 1/(1 + β)(2 − β)(1 + γ)(2 − γ);
-
π j = 2(1 − γ)/(1 + β)(1 + γ)(2 − β)(2 − γ)2;
-
π i = 2(1 − β)/(1 + β)(1 + γ)(2 − β)2(2 − γ)2.
3.2 The Agency Model
The timing under the agency model is as follow:
-
1.
Retailers declare revenue sharing rates simultaneously. The revenue sharing rate set by retailer i is \(\alpha_{i} \in \left[ {0,1} \right)\), with manufacturers retaining \(\left( {1 - \alpha_{i } } \right)\) of the revenue.Footnote 10
-
2.
Manufacturers set retail prices simultaneously. The price set by manufacturer j to retailer i is \(p_{i}^{j}.\)
Under this model, \(S^{j}\) controls the retail price and faces the following optimisation problem
The corresponding first-order condition is given by
Given symmetry, we get
R i faces the following optimisation problem
which is solved in Foros et al. (2014).Footnote 11 Given their results, the symmetric equilibrium revenue sharing rates are, denoted as \(\alpha^{*}\)
The symmetric equilibrium retail prices and demand under the agency model, denoted as \(p_{A}^{*}\) and \(q_{A}^{*}\) respectively, are given by
\(p_{A}^{*}\) decreases in γ. \(q_{A}^{*}\) and γ exhibit a U-shape relationship for the same reason as under the wholesale model: Demand is decided by two countervailing effects. However, under the agency model, β does not affect \(p_{A}^{*}\); hence it affects demand only through the negative market size effect.
The following lemma summarises the complete set of symmetric equilibrium results under the agency model:
Lemma 2
Under the agency model, there exists a symmetric equilibrium in which
-
α * = (2 − γ)(1 − β 2)/[2 − γ(1 + β)];
-
\(p_{A}^{*}\) = (1 − γ)/(2 − γ);
-
\(q_{A}^{*}\) = 1/(1 + β)(1 + γ)(2 − γ);
-
\(\pi_{A}^{j}\) = 2β(1 − γ)[2β − γ(1 + β)]/(1 + β)(1 + γ)(2 − γ)2[2 − γ(1 + β)];
-
π iA = 2(1 − β)(1 − γ)/(1 + γ)(2 − γ)[2 − γ(1 + β)].
4 Comparison
In this section we compare the symmetric equilibrium outcomes under the two models. We start with the following proposition:
Proposition 1
In equilibrium, retail prices are lower, quantities demanded are higher, and consumer surplus is higher under the agency model than under the wholesale model.
Proof
Proposition 1 is driven by the elimination of double marginalisation under the agency model. To show this, we write p * as the sum of two mark-upsFootnote 12
As \(p_{A}^{*} = \left( {1 - \gamma } \right)/\left( {2 - \gamma } \right) = w^{*}\), the total mark-up under the agency model is equivalent to the first mark-up under the wholesale model.
Double marginalisation as the driving force indicates that when the second mark-up under the wholesale model becomes zero, there should not be any difference between the equilibrium outcomes under the two models. This is indeed the case as \(\beta \to 1\) and \(\left( {1 - \beta } \right)/ \left( {2 - \beta } \right)\left( {2 - \gamma } \right) \to 0\). The intuition is: When retailers’ services are close substitutes, retailers are neither able to price above costs (i.e.,\(w^{*}\)) under the wholesale model, nor to demand positive shares from the manufacturers under the agency model. Hence, some degrees of differentiation between retailers are essential for us to distinguish between the equilibrium outcomes under the two models. As long as β is smaller than one, we are able to rank the two sets of equilibrium outcomes.
Proposition 2
In equilibrium, there exists a γ′ ∊ [0, 1) such that social surplus is higher under the agency model (A) than under the wholesale model (W) if \(\gamma \in \left[ {0,\gamma^{\prime } } \right)\).
Proof
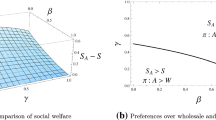
Proposition 2 implies that the agency model is socially desirable given that manufacturers’ goods are sufficiently differentiated. We illustrate the comparison of social surplus (S) between the two models in Fig. 1 to complement Proposition 2. As we observe, when the condition γ ∊ [0, γ ′) is not satisfied, it is still possible for social surplus to be higher under the agency model, but would place additional conditions on β: As γ is close to one, β needs to be closer to zero for social surplus to be higher under the agency model. It follows that the difference in social surplus between the two models is more responsive to changes in differentiation at the manufacturer level.
The results on consumer surplus and social surplus from Propositions 1 and 2 imply that the rank of equilibrium aggregate profits under the two models depends on values of β and γ. Figure 1 and Fig. 2 together offer two more observations that are worth highlighting: First, suppose that both β and γ are independently and equally likely to take up any value over the interval \(\left[ {0,1} \right)\). Then there are more pairs of β and γ such that aggregate profits are lower and social surplus is higher under the agency model than under the wholesale model. Second, as illustrated in Fig. 3, when goods and retail services are approximately homogenous—i.e., \(\beta \to 1\) and \(\gamma \to 1\)—aggregate profits and social surplus are both relatively higher under the wholesale model; when goods and retail services are perfect substitutes—i.e., β = γ = 0—aggregate profits and social surplus are both relatively higher under the agency model.
However, there is a middle region in which social and aggregate outcomes conflict: Social surplus is higher under the agency model, but aggregate profits are higher under the wholesale model. Policy concerns might arise if the wholesale model is adopted. The higher aggregate profits obtained are at the expense of using the “wrong” vertical contract, especially given Proposition 1 that consumer surplus is always higher under the agency model.
We now compare how aggregate profits are divided between manufacturers and retailers under the two models. This not only helps to explain the observed comparison of aggregate profits, but also offers insights on how the power relations between manufacturers and retailers differ under the two models. As vertical restraints theory distinguishes between restraints imposed under manufacturer and retailer power, understanding the division of profits is therefore useful in determining the nature of a particular restraint.
Proposition 3
In equilibrium, manufacturer profits are lower under the agency model than under the wholesale model, whereas there exists a \(\gamma^{\prime \prime } \in \left( {\gamma^{\prime } ,1} \right)\) such that retailer profits are higher under the agency model than under the wholesale model if \(\gamma \in \left[ {0,\gamma^{\prime \prime } } \right)\).
Proof
Under the wholesale model, manufacturers’ per-unit profits are precisely \(w^{*} = \left( {1 - \gamma } \right)/\left( {2 - \gamma } \right)\), whereas under the agency model, their per-unit profits are their shares of \(p_{A}^{*}\),\(\left( {1 -\upalpha} \right)\left( {1 - \gamma } \right)/\left( {2 - \gamma } \right)\), which are strictly lower than \(w^{*}\). Overall for manufacturers, the effect of relatively higher per-unit profits under the wholesale model always outweighs the effect of relatively higher demand under the agency model. In contrast, retailer profits, as illustrated in Fig. 4, are relatively higher under the agency model as along as manufacturers’ goods are sufficiently differentiated—i.e.,\(\gamma\) is not too high, regardless of degrees of differentiation at their own level.
Proposition 3 has two implications: First, moving from the wholesale to the agency model, manufacturers are clearly worse off; therefore, the agency model is never preferred by manufacturers. Instead, the agency model, per se a form of RPM, is likely to be in favour of the retailers. Second, retailers can benefit from high degrees of differentiation at the manufacturer level, implying that the two parties’ incentives are better aligned.
We explain the second implication further: As we assume that firms behave non-cooperatively, they would usually benefit from high degrees of differentiation at their own level and low degrees of differentiation at the other level of the vertically related market, such that they can exercise countervailing power and appropriate a higher portion of industry rents. It follows that a highly differentiated brand would leave thin margins to retailers and high margins to manufacturers (see Steiner 1993).
It is straightforward to verify that this is the case under the wholesale model. The second mark-up in (14), (1 − β)/(2 − β)(2 − γ), increases in \(\gamma\), meaning that retail margin increases as manufacturers’ goods become less differentiated under the wholesale model. Under the agency model, however, retail margin \(\upalpha\left( {1 - \gamma } \right)/\left( {2 - \gamma } \right)\) is positively correlated with degrees of differentiation between goods for any given revenue sharing rate. When the revenue sharing rate is endogenous, the relationship is determined by a trade-off: A higher degree of differentiation between manufacturers can reduce retail margins as it reduces the revenue sharing rate and can increase retail margins as it increases the retail price (which is set by manufacturers). The combined effect may not be the same as under the wholesale model. In fact, for \(\gamma \in \left[ {0,\gamma^{\prime \prime } } \right)\), as stated in Proposition 3, retailers under the agency model actually prefer it when the differentiation between manufacturers’ goods is high.
5 Discussion
In this section we explain how the results that are obtained from the comparison between the wholesale and the agency models are useful for understanding the agency model and the antitrust treatment of restraints of this kind.
First, our results suggest that the agency model may be understood as a retailer power restraint. Retailer power restraints, as introduced in Sect. 1, are usually imposed by insecure manufacturers (Grimes 2007). Ceteris paribus, the agency model is not an option for manufacturers as they earn more under the wholesale model. By choosing the agency model over the wholesale model, manufacturers deliberately create incentives for retailers, at the expense of their own. Although strong manufacturers have no incentive to do so, insecure manufactures may use restraints of this kind to induce retail service and brand promotion (which increases \(\gamma\)). As the vertical relation moves from the wholesale to the agency model, two things change: Retail prices are set by manufacturers instead of by retailers; and transfer payments are revenue shares instead of unit fees. As a result, retailers do not have to compete over prices and the vertical competition between manufacturers and retailers is relaxed, which leaves retailers with higher rents.
Second, with regard to welfare, consumers are better off under the agency model. It follows that if courts were to treat restraints involved in sale and non-sale transactions differently—e.g., in Schwinn the former was illegal whereas the latter was legal—then having legality based on the actual impact of restraints on consumer surplus (and on how such impact differs in sale and non-sale transactions) seems to be more consistent with the definition of the rule of reason,Footnote 13 instead of the legal ownership of property.
The better position of consumers under the agency model further explains, from the overall welfare point of view, why Grimes (2007) might consider that some loose forms of “inducement” offered by insecure manufacturers to retailers are “probably presumptively lawful.” Nevertheless, he retains two concerns over vertical restraints for brand promotion: One is whether such promotion involves deception about product quality that would eventually harm consumersFootnote 14; and the other is whether intrabrand competition is undercut too much to “maintain the competitive distribution of strong brands.” While the first concern is an additional dimension of the problem that the current paper does not deal with, the second concern arises naturally given two possible conflicts: One is between the motive and the impact of a restraint; and the other is between the restraint’s impact on welfare and on competition.
Our final interpretation of results therefore addresses the above conflicts and relates them to antitrust treatment of vertical restraints. Antitrust authorities and courts may frequently face the first conflict. For example, in Schwinn, the Court accepted that the distribution program was for a business purpose that enabled Schwinn to “compete more effectively in the marketplace”Footnote 15; but the question remained was whether “the effect upon competition in the marketplace is substantially adverse.”Footnote 16 This appears to signal that courts attach more weight to the impact on competition.
Within the analysis of the impact of vertical restraints, the second conflict has been controversial alongside the evolution of antitrust treatment. Such conflict is appealing under the agency model given the proceeding discussion: While consumers clearly benefit from it, the agency model is evidently more likely to undercut competition with the alignment of incentives. While this does not mean that the agency model would necessarily harm competition substantially, the lack of incentives for firms to compete may itself constitute a major concern of antitrust authorities and courts. The series of vertical restraint cases suggest that, as highlighted by Martin (2009), if a restraint generates conflicting impacts on competition and consumer surplus, precedence goes to consumer surplus. This implies that, in treating vertical restraints of this kind, the rule of reason may be more appropriate as impacts of such restraints may differ, depending on the context in which they are used and the additional restraints that are used in conjunction, among others.
The move from the per se rule to the rule of reason further highlights the recognition of the importance of intrabrand competition and the powerful position of retailers in some industries. This is because many vertical restraints, including RPM, may not be a means through which manufacturers exercise power, but manufacturers act in response to retailer power. The role of retailers therefore is crucial in determining the status of retailer power restraints, and in particular, identifying cases in which a genuine business purpose is lacking and the restraint is mostly likely to be dictated by retailers.
6 Conclusion
The agency model is popular in some markets in recent years. However, it is not new and involved debatable court decisions. Complementary to studies of the agency model in a particular market, we take an alternative approach to understand the nature of the agency model through comparing it to the wholesale model, as well as through placing it in the context of the antitrust treatment of vertical restraints.
In a bilateral duopoly model with product differentiation at both the manufacturer level and the retailer level of the market, we first find that, relative to the wholesale model, the agency model benefits consumers with lower retail prices as it eliminates double marginalisation. Hence an economic view would suggest that the legality of restraints involved in the agency distribution in Schwinn may be better supported by the impact of restraints on consumer surplus rather than on the legal ownership of property.
Second, as manufacturers are strictly better off under the wholesale model whereas retailers are more likely to be better off under the agency model, the agency model may be an example of retailer power RPM, which is imposed by insecure manufacturers to incentivise retailers to promote their brands. Furthermore, stronger brands do not tend to squeeze retail margin under the agency model; hence the incentives of manufacturers and retailers are better aligned under this model. Overall the agency model increases consumer surplus but tends to relax competition, which constitutes a conflict that is faced by antitrust authorities and courts in treating restraints of this kind. We suggest that they may be evaluated under the rule of reason.
Unlike the traditional views on vertical relations where retailers are often considered to be perfectly competitive and possess little market power, the rise of the agency model implies that, ceteris paribus, retailers are in a strong position. Understanding the agency model as retailer power RPM is meaningful for recognising the changing power relations in some supply and distribution chains.
The potentially better position of retailers under the agency model comes not only from reduced intrabrand competition, but also from relaxed vertical competition given the alignment of incentives. In contrast to the extensive literature on how restraints affect horizontal competition in vertically related markets—i.e., interbrand and intrabrand competition—similar analysis with regard to vertical competition is scarce. While the current paper does not separate the effects that come from the two dimensions, it may be a relevant topic for future research.
Notes
U.S. v. Apple Inc., et al., 12 Civ. 2826 (DLC); The State of Texas, et al. v. Penguin Group Inc., et al., 12 Civ. 3394 (DLC) (2013). In April 2010, five large book publishers in the US switched from the wholesale model of selling e-books, which they used to have with Amazon, to the agency model put forward by Apple. Following the price rise of e-books after the switch of vertical contracts, the Department of Justice lodged a complaint against Apple and the publishers for their contractual agreements including a price parity provision: The most favoured nation (MFN) clause. In July 2013, Apple and the publishers were found to have violated antitrust law. The publishers settled, but Apple appealed. In June 2015, an appeals court upheld the lower court’s decision. Apple sought further review from the Supreme Court, with a claim that its actions enhanced competition. In March 2016, the Supreme Court refused to review the case.
U.S. v. Arnold, Schwinn & Co., 388 U.S. 365 (1966). From the 1950 s, Schwinn adopted a selective distribution system and imposed territorial and customer restraints on its distributors and dealers. Its distributors were authorized to sell only to franchised dealers in their assigned territories, and dealers were allowed to sell only from authorized locations. Meanwhile, its own distribution method, the Schwinn Plan, allowed Schwinn to sell and ship bicycles using various ways and not necessarily through its distributors.
388 U.S. at 379.
Continental T.V. Inc. v. GTE Sylvania, 433 U.S. 36 (1977).
He writes, “In 1952, Schwinn had 22.5% of the market…Schwinn’s share fell to 12.8% by 1961. It was precisely during this period that Schwinn was actively implementing a selective distribution system designed to insulate retailers from competition and allow them to charge a higher margin. Schwinn was, at this point, an insecure brand seller.”
12 Civ. 2826 (DLC) (2013). The publishers were upset by Amazon’s $9.99 prevailing price policy, which they feared would erode the value and price of books, including hardcover books. They agreed to switch from the wholesale to the agency model in response to Apple’s proposal. Apple was found to have “played a central role in facilitating and executing that conspiracy. Without Apple’s orchestration of this conspiracy, it would not have succeeded as it did in the Spring of 2010.”
12 Civ. 2826 (DLC) at 47. “The MFN guaranteed that the e-books in Apple’s e-bookstore would be sold for the lowest retailer price available in the marketplace.” See Foros et al. (2016) for an analysis of how the MFN clause can induce the adoption of the agency model.
For example, Liu and Shuai (2015) view the agency model as vertical integration and neglect the division of industry profits between manufacturers and retailers.
Dobson and Waterson (1996) assume \(\gamma \in \left( { - 1, 1} \right)\) where a negative \(\gamma\) indicates that the goods are complements. We do not consider this case in this paper.
We allow retailers to specify one sharing rate that applies to both manufacturers, and this does not conflict with what we observe in real life. For example, Apple established the same rate to all book publishers, and Google sets the same rate to all apps developers.
Our analysis of retailers’ optimisation problems under the agency model is analogous to Foros et al. (2014).
The first mark-up is \(w^{*}\) as we assume that firms incur zero marginal costs.
“The rule of reason is (127 S. Ct. 2712) ‘the accepted standard for testing whether a practice restrains trade in violation of §1,’ and in application amounts to ‘an inquiry into market power and market structure designed to assess [a restraint’s] actual effect’” (Martin 2009).
Grimes (2007) writes “…the consumer is unaware that a vertical restraint has given the retailer an incentive to promote a particular seller’s product” and that products with “superior characteristics” may “no longer require the promotion incentives of a vertical restraint.”
388 U.S. at 374.
388 U.S. at 375.
References
American Bar Association Section of Antitrust Law. (1977). Monograph No. 2, Vertical restrictions limiting intrabrand competition.
Asker, J., & Bar-Isaac, H. (2014). Raising retailers’ profits: On vertical practices and the exclusion of rivals. American Economic Review, 104(2), 672–686.
Belleflamme, P., & Peitz, M. (2010). Industrial organization: markets and strategies. Cambridge: Cambridge University Press.
Boik, A., & Corts, K. S. (2016). The effects of platform most-favored-nation clauses on competition and entry. Journal of Law and Economics, 59(1), 105–134.
Bork, R. H. (1978). The antitrust paradox: A policy at war with itself. New York: Basic Books.
Condorelli, D., Galeotti, A., & Skreta, V. (2013). Selling through referrals. Working paper.
Dobson, P. W., & Waterson, M. (1996). Product range and interfirm competition. Journal of Economics & Management Strategy, 5(3), 317–341.
Dobson, P., & Waterson, M. (1999). Retailer power: Recent developments and policy implications. Economic Policy, 14(28), 133–164.
Dobson, P. W., & Waterson, M. (2007). The competition effects of industry-wide vertical price fixing in bilateral oligopoly. International Journal of Industrial Organization, 25(5), 935–962.
Foros, Ø., Kind, H. J., & Shaffer, G. (2014). Turning the page on business formats for digital platforms: Does Apple’s agency model soften competition? Working paper.
Foros, Ø., Kind, H. J., & Shaffer, G. (2016). Apple’s agency model and the role of resale price maintenance. Working paper.
Gabrielsen, T. S., & Johansen, B. O. (2015). Buyer power and exclusion in vertically related markets. International Journal of Industrial Organization, 38, 1–18.
Gaudin, G., & White, A. (2014). On the antitrust economics of the electronic books industry. Working paper.
Grimes, W. S. (2007). From Schwinn to Sylvania to where? Historical roots of modern vertical restraints policy. Chapter 5. In E. Fox & D. Crane (Eds.), Antitrust stories. New York: Foundation Press.
Johnson, J. P. (2013). The agency and wholesale models in electronic content markets. Working paper.
Johnson, J. P. (2017). The agency model and MFN clauses. Review of Economic Studies, 84(3), 1151–1185.
Liu, Q., & Shuai, J. (2015). Reverse pricing and revenue sharing in a vertical market. Managerial and Decision Economics, 36(5), 299–313.
Lynch, M. P. (2004). Why economists are wrong to neglect retailing and how Steiner’s theory provides an explanation of important regularities. Antitrust Bulletin, 49, 911–940.
Martin, S. (2009). Industrial organization in context. Oxford: Oxford University Press.
Marvel, H. P., & McCafferty, S. (1996). Comparing vertical restraints. Journal of Economics and Business, 48(5), 473–486.
Mathewson, G. F., & Winter, R. A. (1984). An economic theory of vertical restraints. RAND Journal of Economics, 15(1), 27–38.
Shaffer, G. (1991). Slotting allowances and resale price maintenance: a comparison of facilitating practices. RAND Journal of Economics, 22(1), 120–135.
Steiner, R. L. (1991). Sylvania economics—a critique. Antitrust Law Journal, 60(1), 41–59.
Steiner, R. L. (1993). The inverse association between the margins of manufacturers and retailers. Review of Industrial Organization, 8(6), 717–740.
Telser, L. G. (1960). Why should manufacturers want fair trade? Journal of Law and Economics, 3, 86–105.
Tirole, J. (1988). Theory of industrial organization. Cambridge: MIT Press.
Author information
Authors and Affiliations
Corresponding author
Additional information
I was grateful to Subhasish M. Chowdhury, Bruce Lyons, and Stephen Martin for valuable comments. I appreciate the comments and suggestions of Aditya Bhattacharjea, Daniele Condorelli, Stephen Davies, Amelia Fletcher, Øystein Foros, Germain Gaudin, Jeroen Hinloopen, Morten Hviid, Martin Peitz, and Russell Pittman. I thank seminar participants at the Centre for Competition Policy, Nanjing University and the University of East Anglia. I thank participants at the 5th NIE Doctoral Colloquium, the 10th CRESSE Conference, the 42nd EARIE Conference, and the Workshop for the Special Issue of The Review of Industrial Organization devoted to GTE Sylvania and its aftermath on its 40th anniversary. A previous version of this paper was circulated under the title “A Comparison of the Wholesale Structure and the Agency Structure in Differentiated Markets”. Any remaining mistakes are my own.
Appendix
Appendix
1.1 Proof of Proposition 1
Given Lemmata 1 and 2, it is straightforward that \(p^{*} > p_{A}^{*}\) and \(q^{*} < q_{A}^{*}\) for \(\beta ,\gamma \in \left[ {0, 1} \right)\). Denoting the equilibrium consumer surplus under the wholesale model as CS and that under the agency model as \(CS_{A}\), we find that
Consumer surplus is relatively higher under the agency model if
Since (1 − β)/2(1 + β)2(1 + γ)2(2 − β)2(2 − γ)2 is positive, it follows that CS A − CS > 0 if
The above is equivalent to
which can be easily verified to hold for \(\beta ,\gamma \in \left[ {0, 1} \right).\) \(\square\)
1.2 Proof of Proposition 2
Denoting the equilibrium social surplus under the wholesale model as S and that under the agency model as \(S_{A}\), we can write \(S = 2\pi^{{S^{j} }} + 2 \pi_{{R_{i} }} + CS\) and \(S_{A} = 2\pi_{A}^{{S^{j} }} + 2 \pi_{{R_{i} A}} + CS_{A}\), more specifically,
Given any \(\beta\), the relationship between \(S_{A} - S\) and γ is illustrated in Fig. 5. S A − S is always positive for \(\gamma \in \left[ {0, \gamma^{\prime } } \right)\), whereas it may or may not be positive for \(\gamma \in \left( {\gamma^{\prime } , 1} \right)\). S A = S at \(\gamma = \gamma^{\prime }\). \(\square\)
1.3 Proof of Proposition 3
We first compare manufacturer profits under the two models. Given Lemmata 1 and 2, \(\pi^{{S^{j} }} > \pi_{A}^{{S^{j} }}\) if the following holds
Since 2(1 − γ)/(1 + β)(1 + γ)(2 − β)(2 − γ)2(2 − γ − βγ) is positive, it follows that \(\pi^{{S^{j} }} - \pi_{A}^{{S^{j} }} > 0\) if \(2 - \gamma \left( {1 + \beta } \right) - \beta \left( {2 - \beta } \right)\left( {2\beta - \gamma - \beta \gamma } \right) > 0\). That is, if \(\gamma < 2\left( {1 - \beta^{2} + \beta } \right)/\left( {1 - \beta^{2} } \right)\), which always holds given \(\beta , \gamma \in \left[ {0,1} \right)\).
Next, we compare retailer profits: As illustrated in Fig. 6, given any \(\beta\), \(\pi_{{R_{i} A}} - \pi_{{R_{i} }}\) is positive for \(\gamma \in \left[ {0, \gamma^{\prime \prime } } \right)\), whereas it is more likely to be negative for \(\gamma \in \left( { \gamma^{\prime \prime } , 1} \right)\). To find \(\gamma^{\prime \prime }\), we evaluate \(\pi_{{R_{i} A}} = \pi_{{R_{i} }}\) at β = 0, and obtain \(\gamma^{\prime \prime } = 3/4\). \(\square\)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lu, L. A Comparison of the Wholesale Model and the Agency Model in Differentiated Markets. Rev Ind Organ 51, 151–172 (2017). https://doi.org/10.1007/s11151-017-9583-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11151-017-9583-y