Abstract
We analyze cooperation of individuals in a family context, using a Public Good game. In a lab experiment, 165 individuals from 55 three-generation families (youth, parent, and grandparent) play a repeated Public Good game in three different treatments: one in which three members of the same family play each other (family), a second with the youth and two non-family members, while preserving the previous generational structure (inter-generational), and a third in which three randomly-selected players play each other (random). We find that all the age groups cooperate more when playing with relatives, indicating that family ties may have a positive relationship to contributions to the Public Good. We also find that this trend is more evident for the youths and the parents than for the grandparents. Furthermore, young individuals tend to cooperate less than older generations, especially in non-family treatments. Our results serve as evidence of the relationship between family ties and inter-generational cooperative behaviors.



Similar content being viewed by others
Notes
Munro (2015) offers a review of the literature on this issue, along with certain methodological observations.
In the IG treatment, we impose the restriction that none of the players are from the same family, which assures that individuals playing in the IG treatment are different from individuals playing in the F treatment. However, in the R treatment, we do not impose any restriction on the players, and it could be that players from the same families could be matched in the same group. The probability that in the R treatment all the players were from different families was very low (e^(−3) = 5%), and thus in 10 groups two members of the same household were matched to play the game. No groups have all three members from the same household. Despite that there were several groups with players from the same households, we cannot hypothesize that family ties were influencing the behavior of players, as the game was completely anonymous and players did not know with whom they were playing.
In each round, each player had up to 20 seconds to choose how much to contribute to the pool. After 20 seconds, the system randomly chose for them, but then the players could continue to choose without problems in the following rounds. Up to 4,950 total contributions made during the experiment, 141 (2.85%) contributions were done by the system, which represents a low percentage and does not bias our main results.
The amount given to the volunteers may seem low in comparison to Peters et al. (2004), although it is not low in comparison with other experiments (Gutierrez-Roig et al. 2014; Poncela-Casasnovas et al. 2016). In fact, the payment/hour is quite high, as the sessions lasted around 20 min (10€ for 20 min = 30€ per hour). In any case, the amount of the attendance fee was not described during the process of recruitment, and volunteers knew the total amount assigned to them only at the end of the experiment. Furthermore, during the recruitment process it was announced that a tablet would be raffled among all the volunteers at the end of the experiment. Also, snacks were offered after (first session) and before (second session) each session.
Panel A of Table B1 in the Supplementary Appendix shows the average contributions of players, by generation. The average contributions of youths, parents, and grandparents are 5.05, 6.21 and 5.95, with the differences in the average contributions across the 3 generations being statistically significant at the 99% confidence level.
Panel B of Table B1 in the Supplementary Appendix shows average contributions of players, by treatment. The average contributions in the F, IG and R treatments are 6.77, 5.27 and 5.17, with the differences in the average contributions across the 3 treatments being statistically significant at the 99% confidence level.
The results do not differ significantly between the IG and R treatments, but this is not at all surprising. The second group includes the youth and two non-family members, and there is a 1 in 55 chance that a youth will have a parent and a 1 in 55 chance of having a grandparent within the same game (1/55*55 chance of having both of them in the same play). These probabilities are very low, which may explain why the average contributions in the two treatments are similar.
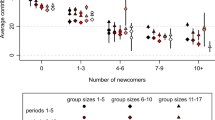
In order to measure within-group differences in the previous round, there is no obvious choice for a measure to compare individual contributions relative to the other players’ contributions. Despite that we select the average contributions of the other players, this measure does not differentiate the situations when the other two members have behaved very differently. Alternative measures could be the maximum or minimum of the other players’ contributions.
We include proportional weights such that the size of the dot in the figure reflects the proportion of contributions included in it. We have added a linear fit to determine the extent to which scatters are distributed following a linear relationship.
The time variation needed to estimate a panel data model is given by the fact that respondents play more than one round during each phase. The use of Random Effects estimators leads to the assumption that individual heterogeneity plays the same role across all treatments, as if some individuals have a kind of “natural propensity to cooperate”, depending on observed (gender, cooperation) and unobserved characteristics. The data set does not allow us to test for this assumption (and it may not be the case), and we leave this issue for future research. However, our results are consistent to the estimation of models where the unobserved heterogeneity of individuals is not considered, such as OLS models, and thus we expect that our conclusions do not change when issues of unobserved heterogeneity are taken into account. Furthermore, our results are consistent to the use of Fixed Effects models (available upon request).
Prior research on cooperation, using experiments, has found mixed results from a gender perspective, although recent evidence appears to point toward women being more cooperative than men, from a social dilemma perspective (Molina et al. 2013). In the framework of the work-division within couples, research has found that there are gender differences in the contribution to the household Public Good (Thomas 1990; Hoddinott and Haddad 1995; Lundberg et al. 1997; Cochard et al. 2017), with a possible explanation being a greater sensitivity to social context by women (Ledyard 1995; Eckel and Grossman 2008; Croson and Gneezy 2009; Balliet et al. 2011).
Given that the order of treatments is reversed in the second group, compared to the first group, this may affect the results. To disentangle this possible effect, we have analyzed the average contribution to the Public Good game, by group, treatment, and session. The average contributions in the F, IG, and R treatments in the first group are 6.01, 4.89, and 4.91, respectively, while the average contributions in the F, IG, and R treatments in the second group are 7.99, 5.88, and 5.60 (results are available upon request). Thus, the differences in the average contribution between the two groups are 1.98, 0.99, and 0.69 for the F, IG and R treatments, respectively, with such differences being statistically significant at standard levels.
In order to analyze whether there are gender differences in cooperation in, for example, the round number or the treatment, we have interacted all our controls of Equation (1) with the gender dummy. We find no differences according to the gender of individuals, and results are consistent with the positive relationship between family ties and cooperative behavior (results available upon request).
We test whether the linear combinations obtained for parents (e.g., 2.53–0.85) and grandparents (e.g., 2.53–1.58) are statistically significant or not. To that end, we use a Wald-type test to test whether the linear combination can be considered to be zero (Ho, null hypothesis) or different from zero (Ha, Alternative hypothesis). We obtain that the linear combinations are statistically significant, which indicates that the contributions of parents and grandparents are higher in the F treatment than in the R treatment.
We also test if the effect of the F treatment is different by generation. To that end, we apply Wald-type tests on the difference between the coefficients for youths (2.533), parents (2.53–0.85) and grandparents (2.53–1.58). We observe that the differences are statistically significant at standard levels, which indicates that playing with family members increases the contribution of players differently for each generation.
References
Andreoni, J. (1988). Why free ride? Strategies and learning in Public Good games. Journal of Public Economics, 37, 291–304.
Andreoni, J. (1990). Impure altruism and donations to Public Good: a theory of warm-glow giving. Economic Journal, 100, 464–477.
Andreoni, J., & Croson, R. (2008). Partners versus strangers: random rematching in public good games, In C. Plott & V. Smith (Eds.), Handbook of Experimental Economic Results (pp. 776–782). Amsterdam: North-Holland Publications, North-Holland.
Balliet, D., Li, N. P., Macfarlan, S. J., & Van Vugt, M. (2011). Sex differences in cooperation: a meta-analytic review of social dilemmas. Psychological Bulletin, 137, 881–909.
Beblo, M., & Beninger, D. (2017). Do husbands and wives pool their incomes? A couple experiment. Review of Economics of the Household, 15, 779–805.
Becker, G. S. (1962). Investment in human capital: a theoretical analysis. Journal of Political Economy, 70, 9–49.
Becker, G.S. (1974). A Treatise on the Family. Cambridge, Massachusetts: Harvard University Press.
Blake, P. R., Rand, D. G., Tingley, D., & Warmeken, F. (2015). The shadow of the future promotes cooperation in a repeated prisoner’s dilemma for children. Scientific Reports, 5, 14559.
Charness, G., & Villeval, M. C. (2009). Cooperation and competition in intergenerational experiments in the field and the laboratory. American Economic Review, 99, 956–978.
Chaudhuri, A. (2011). Sustaining cooperation in laboratory Public Good games: a selective survey of the literature. Experimental Economics, 14, 47–83.
Chowdhury, S. M., & Jeon, J. Y. (2014). Impure altruism or inequality aversion?: an experimental investigation based on income effects. Journal of Public Economics, 118, 143–150.
Cox, D. (1987). Motives for private transfers. Journal of Political Economy, 95, 508–546.
Cochard, F., Couprie, H., & Hopfensitz, A. (2017). What if women earned more than their spouses? An experimental investigation of work-division in couples. Experimental Economics, 11, 1–22.
Croson, R. (2007). Theories of commitment, altruism and reciprocity: evidence from linear Public Good games. Economic Inquiry, 45, 199–216.
Croson, R., & Gneezy, U. (2009). Gender differences in preferences. Journal of Economic Literature, 47, 448–474.
Crumpler, H., & Grossman, P. J. (2008). An experimental test of warm glow giving. Journal of Public Economis, 92, 1011–1021.
Dauphin, A., Fortin, B. & Lacroix, G. (2017). Is consumption efficiency within households falsifiable? Review of Economics of the Household. https://doi.org/10.1007/s11150-016-9359-4.
Duffy, J., & Ochs, J. (2009). Cooperative behavior and the frequency of social interaction. Games and Economic Behavior, 66, 785–812.
Eckel, C.C., & Grossman, P. J. (2008). Differences in the economic decisions of men and women: experimental evidence. In C. Plott, & V. Smith (Eds), Handbook of Experimental Economic Results (pp. 509–519). Amsterdam: North-Holland Publications.
Fehr, E., Bernhard, H., & Rockenbach, B. (2008). Egalitarianism in young children. Nature, 454, 1079–1083.
Fehr, E., Rützler, D. & Sutter, M. (2011). The development of egalitarianism, altruism, spite and parochialism in childhood and adolescence, IZA Discussion Paper No. 5530.
Fischbacher, U., & Gächter, S. (2010). Social preferences, beliefs, and the dynamics of free riding in Public Good games. American Economic Review, 100, 541–556.
Fischbacher, U., Gächter, S., & Fehr, E. (2001). Are people conditionally cooperative? Evidence from a Public Good games. Economics Letters, 71, 397–404.
Görges, L. (2015). The power of love: a subtle driving force for unegalitarian labor division? Review of Economics of the Household, 13, 13–192.
Gracia-Lázaro, C., Ferrer, A., Ruiz, G., Tarancon, A., Cuesta, J. A., Sánchez, A., & Moreno, Y. (2012). Heterogeneous networks do not promote cooperation when humans play a Prisoner’s Dilemma. Proceedings of the National Academy of Sciences of the United States of America, 109, 12922–12926.
Grujić, J., Gracia-Lázaro, C., Milinski, M., Semmann, D., Traulsen, A., Cuesta, J. A., Moreno, Y., & Sánchez, A. (2012). A comparative analysis of spatial Prisoner’s Dilemma experiments: conditional cooperation and payoff irrelevance. Scientific Reports, 4, 4615.
Gutiérrez-Roig, M., García-Lázaro, C., Perelló, J., Moreno, Y., & Sánchez, A. (2014). Transition from reciprocal cooperation to persistent behaviour in social dilemas at the end of adolescence. Nature Communications, 5, 4362.
Hamilton, W. D. (1964). The genetical evolution of social behaviour. Journal of Theoretical Biology, 7, 1–52.
Hoddinott, J., & Haddad, L. (1995). Does female income share influence household expenditures? Evidence from Côte d’Ivoire. Oxford Bulletin of Economics and Statistics, 57, 77–96.
Isaac, R. M., & Walker, J. (1988). Group size effects in Public Good provision: the voluntary contributions mechanism. Quarterly Journal of Economics, 103, 179–200.
Ledyard, J. O. (1995). Public Good: a survey of experimental research. In A. E. Roth, & Kagel, J. H. (Eds.), Handbook of experimental economics. (pp. 111–194). Princeton: Princeton University Press.
Lundberg, S. J., Pollak, R. A., & Wales, T. L. (1997). Do husbands and wives pool their resources? Evidence from the United Kingdom child benefit. Journal of Human Resources, 32, 463–480.
Molina, J. A., Giménez-Nadal, J. I., Cuesta, J. A., García Lázaro, C., Moreno, Y., & Sanchez, A. (2013). Gender differences in cooperation: experimental evidence on high school students. Plos One, 8, e83700.
Muller, L., Sefton, M., Steinberg, R., & Vesterlund, L. (2008). Strategic behavior and learning in repeated voluntary contribution experiments. Journal of Economic Behavior and Organization, 67, 782–793.
Munro, A. (2015). Intro-household Experiments: a survey and some methodological observations. GRIPS Discussion Paper N°15-03.
Nowak, M. A., & May, R. M. (1992). Evolutionary games and spatial chaos. Nature, 359, 826–829.
Oli, M. K. (2003). Hamilton goes empirical: estimation of inclusive fitness from life-history data. Proceedings of the Royal Society Biological B, 270, 307–311.
Palfrey, T. R., & Prisbrey, J. E. (1996). Altruism, reputation, and noise in linear Public Good games. Journal of Public Economics, 61, 409–427.
Peters, H. E., Ünür, A. S., Clark, J., & Schulze, W. D. (2004). Free-riding and the provision of Public Good in the family: a laboratory experiment. International Economic Review, 45, 283–299.
Poncela-Casasnovas, J., Gutiérrez-Roig, M., Gracia-Lázaro, C., Vicens, J., Gómez-Gardeñes, J., Perelló, J., Moreno, Y., Duch, J., & Sánchez, A. (2016). Humans display a reduced set of consistent behavioral phenotypes in dyadic games. Science Advances, 2, e1600451.
Porter, M., & Adams, A. (2016). For love or reward? Characterising preferences for giving to parents in an experimental setting. The Economic Journal, 126, 2424–2445.
Reynolds, S. A. (2015). Behavioral games and intrahousehold allocation: teenage mothers and their mothers in Brazil. Review of Economics of the Household, 13, 901–927.
Thomas, D. (1990). Intra-household resource allocation: an inferential approach. Journal of Human Resources, 25, 635–664.
Waibel, M., Floreano, D., & Keller, L. (2011). A Quantitative test of Hamilton’s rule for the Evolution of Altruism. PloS Biology, 9, 1–7.
West, S. A., Murray, M. G., Machado, C. A., Griffin, A. S., & Herre, E. A. (2011). Testing Hamilton’s rule with competition between relatives. Nature, 409, 510–513.
Acknowledgements
We are grateful to the IBERCIVIS Foundation for organizing volunteer recruitment. This paper has benefited from funding by the Spanish Ministry of Economics (Project ECO2012-34828), the EU FET Proactive Project Dolfins (Grant 640772) and FET Open Project IBSEN (Grant 662725). This paper was partially designed while Jose Alberto Molina was Visiting Fellow at the Department of Economics of Boston College (US), to which he would like to express his thanks for the hospitality and facilities provided.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Electronic supplementary material
Rights and permissions
About this article
Cite this article
Molina, J.A., Ferrer, A., Giménez-Nadal, J.I. et al. Intergenerational cooperation within the household: a Public Good game with three generations. Rev Econ Household 17, 535–552 (2019). https://doi.org/10.1007/s11150-018-9414-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11150-018-9414-4