Abstract
In liberalized network industries, competitors can either compete for service using the existing infrastructure (access) or deploy their own capacity (bypass). We revisit this make-or-buy problem making two contributions to the literature. First we analyze both the profit maximizing behavior of an incumbent and the welfare maximizing behavior when the entrant chooses between access and bypass. Second, we extend the baseline model studied in the literature by allowing for fixed costs of network installation. By analogy to the literature on strategic entry deterrence, we distinguish three régimes of blockaded bypass, deterred bypass and accommodated bypass depending on the entrant’s unit cost. We show that the make-or-buy decision of the entrant is not necessarily technologically efficient: when bypass is chosen, it is always the cheapest option but access may be chosen when it is not cost effective.



Similar content being viewed by others
Notes
While we cast our analysis in the framework of network industries, it covers more generally any situation where a vertically integrated incumbent faces an entrant who can choose to make an input or buy it from the incumbent.
See Laffont and Tirole (1994).
For example, in the UK, the regulator OFCOM has decided that some local broadband markets are sufficiently competitive for access regulations to be lifted.
The Belgian regulators impose mandatory third-party access to the cable-TV network, the Canadian regulators have recently imposed regulated access for optical fibre networks.
The analogy between bypass and entry deterrence, while useful, is not complete. The model of competition with access is more complex than a simple model of competition because of the interactions between the access and retail markets. Existing results on entry deterrence cannot be directly applied to bypass deterrence.
Mandy (2009) shows that in the absence of fixed cost the make or buy decision of the entrant is technologically efficient for a broad range of access charges.
For Cave and Vogelsang (2003), service-based competition allows newcomers in the industry to invest progressively in their own infrastructure, first in replicable assets (e.g., long-distance conveyance facility) then in less replicable ones (e.g., local loop). When there are ladders of investment, leasing part of the existing infrastructure is then essential for the development of facility-based competition. Accordingly, a low access charge accelerates the deployment of alternative infrastructures. For Bourreau and Dog̃an (2005), allowing for access delays investment in competing infrastructures because the cost of a new infrastructure includes an opportunity cost equal to the profit realized under service-based competition (an effect that is similar to the replacement effect in innovation races). Following that, a lower access price increases the opportunity cost of bypass and should delay further infrastructure building. In an international study using a sample of OECD countries, Bouckaert et al. (2010) found that mandatory access to the incumbent DSL networks negatively affects the incentives to invest in alternative broadband networks.
Notice that \(\delta \) cannot be strictly interpreted as a parameter of product differentiation in the utility function, as utility explodes to \(+ \infty \) or \(-\infty \) when \(\delta \) goes to 1.
Allowing for different retail costs would introduce an additional dimension of heterogeneity of the model, greatly complicating the computations with little additional insight.
The exact computations for the linear model involve tedious expressions and are deferred to the Appendix which contains all explicit formulae.
Sappington (2005) labels this effect the opportunity cost of access.
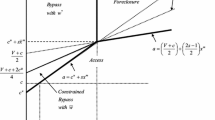
In our model, there is a commitment to the access charge which is set prior to the decision of the entrant on whether to bypass the incumbent’s network. Absent this commitment, the incumbent would have incentives to raise the access price (to \(w^*\)) after access has been chosen by the entrant. Commitment to the access price is thus essential for the existence of the bypass deterrence régime.
Vickers (1995) was the first to identify that an access price below the induced cost might be optimal, in his case to curb the entrant’s market power.
These values guarantee a positive profit for firm 1 if we assume that \(f_1=f_2\).
However, with a negative margin on access, the incumbent may resist the imposition of the access charge \(\hat{w}\) and resort to sabotage in order to protect its profit on the downstream market.
Bloch and Gautier (2008) found the same result in a different model where the regulator has the ability to set both the access and retail prices.
For simplicity, we consider the same range of access charges as Mandy (2009). However our analysis also extends to the optimal access charges set by the incumbent and the regulator even if they fall outside this interval.
References
Avenali, A., Matteucci, G., & Reverberi, P. (2009). Dynamic access pricing and investment in alternative infrastructures. International Journal of Industrial Organization, 28, 167–175.
Bloch, F., & Gautier, A. (2008). Access pricing and entry in the postal sector. Review of Network Economics, 7, 207–230.
Bouckaert, J., van Dijk, T., & Verboven, F. (2010). Access regulation, competition, and broadband penetration: An international study. Telecommunications Policy, 34, 661–671.
Bourreau, M., & Dog̃an, P. (2005). Unbundling the local loop. European Economic Review, 49, 173–199.
Bourreau, M., Dog̃an, P., & Manant, M. (2010). A critical review of the “Ladder of Investment” approach. Telecommunications Policy, 34, 683–696.
Cave, M., & Vogelsang, I. (2003). How access pricing and entry interact. Telecommunications Policy, 27, 717–727.
Chen, Y. (2001). On vertical mergers and their competitive effects. RAND Journal of Economics, 32, 667–685.
Gayle, P., & Weisman, D. (2007). Are input prices irrelevant for make-or-buy decisions? Journal of Regulatory Economics, 32, 195–207.
Laffont, J.-J., & Tirole, J. (1994). Access pricing and competition. European Economic Review, 38, 1673–1710.
Mandy, D. (2009). Pricing inputs to induce efficient make-or-buy decisions. Journal of Regulatory Economics, 36, 29–43.
Marcus, J. (2005). Is the U.S. dancing to a different drummer? Communications & Strategies, 60, 39–58.
Nardotto, M., Valletti, T., & Verboven, F. (2015). Unbundling the incumbent: Evidence from the UK broadband. Journal of the European Economic Association, 13, 330–362.
Sappington, D. (2005). On the irrelevance of input prices for make-or-buy decisions. American Economic Review, 95, 1631–1638.
Schwarz, A. (2007). Wholesale market definition in telecommunications: The issue of wholesale broadband access. Telecommunications Policy, 31, 251264.
Tirole, J. (1988). The theory of industrial organization. Cambridge, London: MIT Press.
Vickers, J. (1995). Competition and regulation in vertically related markets. Review of Economic Studies, 62, 1–17.
Vogelsang, I. (2013). The endgame of telecommunications policy? A Survey, Review of Economics, 64, 193–270.
Author information
Authors and Affiliations
Corresponding author
Additional information
We are grateful to the editor, two anonymous referees, M. Armstrong, P. Belleflamme, C. Cambini, F. Etro, B. Lyons, K. Mizuno and conference participants at the IIOC (Washington) and EARIE (Roma) for helpful comments. This research was funded through the ARC Grant for Concerted Research Actions, financed by the French-speaking Community of Belgium.
A The linear model
A The linear model
In this Appendix, we use the linear demand functions defined in Eq. (1) to derive the explicit functional forms for the equilibrium prices, quantities and profits and to check our comparative static results. Lemmas are proven using these explicit formulae. The linear model allows us to derive the thresholds for the access charge \(\omega ^e\) and \(\omega ^l\) and for the cost \(c^D\), \(c^B\), \(c^W\) and \(c^I\) as they are the solution to second degree equations. These expressions are used for our numerical simulations reproduced in Tables 1 and 2.
Equilibrium prices and quantities under access Profits under access are defined as:
From the profit functions, we can derive the unique equilibrium prices and the corresponding quantities for any given w:
It is straightforward to check that equilibrium prices are increasing in w and the corresponding equilibrium quantities are decreasing. The equilibrium profits are given by:
The profit functions are quadratic in w, \( {\tilde{\pi }}_1^a\) is concave in w and \(\frac{\partial {\tilde{\pi }}_2^a}{ \partial w}<0\). The profit maximizing access charge \(w^*\) is defined as:
Equilibrium prices and quantities under bypass Profits under bypass are defined as:
Solving for the linear demand model, equilibrium prices, quantities and profits are given by:
And the standard comparative static results apply: \(\frac{\partial {\tilde{p}}_i^b}{\partial c_i}>\frac{\partial {\tilde{p}}_i^b}{\partial c_j}>0\), \(\frac{\partial {\tilde{\pi }}_i^b}{\partial c_i}<0 \) and \(\frac{\partial {\tilde{\pi }}_i^b}{\partial c_j}>0\).
Proof of Lemma 1
The proof of Lemma 1 can be easily done by replacing w and \(c_2\) by x in \({\tilde{p}}_i^a\) and \({\tilde{p}}_i^b\). Then, we have that:
And the lemma is proven. \(\square \)
Limit and equivalent access charges Solving Eq. (10), we find the limit access charge \(\omega ^l\):
And \(\omega ^l\) is increasing in both \(c_2\) and \(f_2\). When the entrant has no fixed cost (\(f_2=0\)), then \(\omega ^l= \frac{c_2(2-\delta ^2) - c_1 \delta ^2}{2(1-\delta ^2)}\) and it is easy to check that \(\omega ^l> c_2\) if \(c_2> c_1\) and \(\omega ^l< c_2\) if \(c_2< c_1\). The equivalent access charge is the solution to Eq. (11) but it is not reproduced here as the expression is complicated and has no value-added.
Proof of Lemma 2
To check that Lemma 2 is satisfied, note that:
\(\square \)
Proof of Lemma 3
We check that Lemma 3 is satisfied by noting that \(\frac{\partial {\tilde{\pi }}_1^{a}(w) }{\partial w} \frac{\partial w^l(x)}{\partial x}- \frac{\partial {\tilde{\pi }}_1^{b}(x)}{\partial x} \) is a decreasing function of x. Hence, \(\frac{\partial {\tilde{\pi }}_1^{a}(w) }{\partial w} \frac{\partial w^l(x)}{\partial x}- \frac{\partial {\tilde{\pi }}_1^{b}(x)}{\partial x} > 0\) if and only if the function is positive when \(x = c_1\) and \({\tilde{w}}_2(x)= c_1\). Computations show that, at this point,
\(\square \)
which is a linear function of \(c_1\) and is positive for all \(0< \delta < 1\) both at \(c_1=0\) and at \(c_1=1\), showing that the lemma is satisfied.
Welfare and regulation
It is easy to check that the welfare under access is concave in the access charge:
We can thus identify an access charge \({\hat{w}}\) that maximizes the welfare function \(W^a\):
However, the incumbent’s profit \(\pi _1^a({\hat{w}})\) is negative and the access charge \({\hat{w}}\) does not satisfy the constraint \({\hat{w}}\ge \omega _0\) even for \(f_1=0\):
The welfare under bypass is decreasing in the entrant’s cost \(c_2\):
Rights and permissions
About this article
Cite this article
Bloch, F., Gautier, A. Strategic bypass deterrence. J Regul Econ 52, 189–210 (2017). https://doi.org/10.1007/s11149-017-9337-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11149-017-9337-7