Gibbs Paradox as a Derivative of Composition Entropy

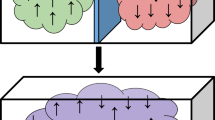
In science, so-called “problem tasks” sometimes arise, the solution of which has been sought for a long time by several generations of scientists. Possessing deep knowledge and developed intuition, they sometimes predict the result of a problem, but they cannot find a solution. Among such problems of science can be attributed the problem that entered physics under the name “Gibbs paradox”. Gibbs predicted all the properties of the entropy of a mixture. He showed that when two different gases are mixed, the entropy of the mixture exceeds the sum of the initial entropies of the components by a value called the jump of entropy. However, he was unable to explain the physical nature of this jump. The fact is that its value does not depend on the nature of gases and has the same value for a mixture of gases of any arbitrary chemical composition. For more than a century, there has been the Gibbs paradox associated with the fundamental parameter of physical systems — entropy, and so far no one has been able to clarify this paradox or at least find out what causes it to form.