Introduction

It is well known now that almost all processes in chemistry, physical chemistry and biochemistry depend in a nonlinear manner on the values of key variables, like concentrations of chemical species in a reaction, and therefore, their evolution in time and their dynamic states most often must be analyzed by means of the main principles of nonlinear dynamics. These complex nonlinear reaction systems can be in various dynamic states such as regular oscillations, period-doubling, quasi-periodicity and deterministic chaos. In addition to the experimental examination of the remarkable behavior of these systems, which provides numerous qualitative and quantitative data, the theoretical investigations including mechanistic consideration [1, 2] and numerical simulations of oscillatory processes allow the development and refinement of their reaction mechanisms. Modelling of these complex processes is not an easy task since oscillatory reactions consist of a lot of reaction steps including numerous independent intermediate species [3]. In mathematical terms, the corresponding models consist of many variables and kinetic equations. However, a wide variety of their dynamical states is very useful in examinations of the proposed reaction mechanism [4,5,6]. Thus, for establishing and refining a reaction model, here we used experimentally obtained dynamical states as a function of temperature, that is, we used the bifurcation diagram where temperature was the control parameter. Namely, we intend to show the importance of the bifurcation analysis, i.e. the bifurcation diagram role in fine tuning of a model for complex nonlinear reaction system, more precisely of one variant of a model for the Bray–Liebhafsky oscillatory reaction [7, 8].

The Bray–Liebhafsky (BL) oscillatory reaction [9, 10] involves iodate-catalyzed decomposition of hydrogen peroxide in an aqueous solution of sulfuric acid:

$${\text{2}}\,{\text{H}}_{{\text{2}}} {\text{O}}_{{\text{2}}} \mathop{\longrightarrow}\limits^{{\text{H}}^{+},\,\text{IO}_{3}^{- }}{\text{2}}\,{\text{H}}_{{\text{2}}} {\text{O + O}}_{{\text{2}}}$$

Under defined experimental conditions, a cascading hydrogen peroxide consumption and oxygen evolving as well as an oscillatory evolution of the iodine intermediates (I2, I−, HIO, HIO2, etc.) occurs.

The Bray–Liebhafsky oscillatory reaction is an excellent example of a complex nonlinear dynamic system, in which various nonlinear phenomena have been found by experimental investigation as well as by theoretical analysis of model mechanisms. All these examinations were done either under closed system (batch) conditions [7, 11,12,13,14,15,16,17,18,19,20,21,22,23,24,25] or under an open system, i.e. continuous well-stirred tank reactor (CSTR) conditions [26,27,28,29,30,31,32,33,34,35,36,37]. In the CSTR, an oscillatory system can be maintained far from thermodynamic equilibrium indefinitely, with constant values of the control parameters such as temperature, inflow concentration of constituents and specific flow rate. By variation of a control parameter, the evolution of dynamic states can be examined, and obtained bifurcation diagram showing regions of the parameter space in which qualitatively different dynamic states occur (stable steady state, oscillatory and chaotic ones) can be generated. Dynamical behavior examinations in the CSTR are not only significant for mechanistic studies, but also for better understanding of complex reaction systems in general.

Different experimentally observed nonlinear phenomena can be numerically simulated using a several postulated models and their variations that defines the mechanism of BL oscillating reaction. The first model of the BL reaction where a direct autocatalytic step was successfully substituted by a realistic autocatalytic loop was proposed by Schmitz [38]. Building on this core of a model consisting of six reactions (R1–R6, Table 1), where three of them are reversible, new variants of a model for the BL reaction were proposed. Thus, these variants of the BL oscillatory reaction model consists of mentioned six reaction expanded by one additional reaction (R7, Table 1) [14] or by two additional ones (R7 and R8, Table 1) [7]. Later, the influence of oxygen and iodine evaporation was analyzed by the addition of these reactions into the model [21]. A systematic analysis of the most probable reactions in modelling procedure is presented in papers published by Schmitz [23, 25, 39,40,41,42,43,44]. However, the variant of the model consisting of eight reactions R1–R8, denoted as M(R1–R8) (Table 1), supplies a basic form for simulating different experimentally obtained nonlinear phenomena and, therefore, it has been widely applied [7, 21, 29, 36, 45]. Also, it was found later that the model of BL reaction M(R1–R8) can be reduced to a simpler form, more appropriate for theoretical investigations, but without losing the ability to simulate complex dynamic states, such as mixed-mode oscillations, period doubling and deterministic chaos, denoted here as M(R1–R6, R8) [8]. This variant of the BL oscillatory reaction, i.e. the model M(R1–R6, R8), consists of seven reactions (first six reactions (R1–R6) and the eighth one (R8), Table 1). To simulate the dynamic behavior in the CSTR, regardless of which variant of the model is used, the original set of chemical reactions with corresponding rate expressions and rate constants is expanded only by first order reactions to take care of the flows [28]. So, in the model M(R1–R8), or M(R1–R6, R8), first eight, or seven reactions describe the mechanism of the process in batch reactor, whereas these reactions expanded by seven reactions caused by flows must be taken into account when BL oscillatory reaction studied in a CSTR.

Table 1 A model M(R1–R8) of the Bray–Liebhafsky reaction in the CSTR
Full size table

Although all the above mentioned models of BL reaction can successfully simulate oscillatory dynamic states, neither this given in Table 1, nor any other can describe all the experimentally obtained phenomena perfectly. Particularly, the model shown in Table 1, although suitable for simulating mixed-mode sequences, does not reproduce well position of bifurcation points. With the aim to see if this is due to the ill postulated model or to inadequate kinetic parameters, we applied bifurcation analysis on the BL reaction model given in Table 1. Since kinetic parameters are very difficult to obtain by independent experimental investigations of oscillatory processes in the steady states far from thermodynamic equilibrium, we hope to obtain more reliable parameter values by adjusting simulated bifurcation diagram to the experimental one. In addition, we intend to show that for rate constants determination, bifurcation diagram of the considered reaction system can be used in the form of minima and maxima of the oscillations characteristic for given dynamic state, as a function of the control parameter value.

The model system

The model given in Table 1, consisting of seven reaction steps (R1–R6 and R8), where three of them are reversible (R1, R3 and R4), together with seven flow steps (f1–f7), was used for the numerical simulations of the dynamic states of the BL oscillatory reaction under CSTR conditions.

In this model, there are six linearly independent intermediate species (H2O2, I2, I–, HIO, HIO2 and I2O). A more elaborated discussion of such approximation is given elsewhere [8]. In numerical simulations it was postulated that hydrogen peroxide is the only inflow species. In Table 2, rate laws are listed along with rate constants (at T = 60.0 °C) and activation energies E a,1−E a,8 determined on the basis of available experimental data as well as theoretical consideration of the system stability [7, 8, 46,47,48]. The reaction notations are preserved for an easier comparison with the previous results.

Table 2 Rate laws, rate constants [7, 8, 48] and activation energies [18, 46, 47] used in numerical simulations of the Bray–Liebhafsky reaction at T = 60.0 °C
Full size table

Here, [H2O2]in and j 0 denotes the inflow of hydrogen peroxide concentration and a specific flow rate, respectively; r i , r +i and r −i denote the rates of the whole reactions i (i = 1–8), their forward parts and their reverse parts, whereas r fj denotes rates of reactions j (j = 1–7) caused by flows (Table 2). In numerical simulations, the approximately constant concentrations of water ([H2O] = 55 mol L−1) is included in corresponding rate constants. The concentrations of iodate and hydrogen ions are taken as constant in simulations and also included in corresponding rate constants.

Thus, in a CSTR, where the inflow of hydrogen peroxide and outflow of all species are present, the dynamics of the model, i.e. time evolution of the concentration of H2O2, I2, I−, HIO, HIO2 and I2O, can be described by the following set of differential equations based on the considered variant of a model [8] and mass action kinetics [49, 50]:

$${\text{d}}\, [ {\text{H}}_{ 2} {\text{O}}_{ 2} ] / {\text{d}}t\;{ = }\; - r_{ 5} - r_{ 6} - r_{ 8} + j_{ 0} \, ( [ {\text{H}}_{ 2} {\text{O}}_{ 2} ]_{\text{in}} - [ {\text{H}}_{ 2} {\text{O}}_{ 2} ] )$$
(1)
$${\text{d}}\, [ {\text{I}}_{ 2} ] / {\text{d}}t\;{ = }\;r_{ + 4} - r_{ - 4} - j_{ 0} \, [ {\text{I}}_{ 2} ]$$
(2)
$${\text{d}}\, [ {\text{I}}^{ - } ] / {\text{d}}t = - \,r_{ + 1} + r_{ - 1} - r_{2} - r_{ + 4} + r_{ - 4} + r_{5} - j_{0} \, [ {\text{I}}^{\text{ - }} ]$$
(3)
$${\text{d}}\, [ {\text{HIO]/d}}t = r_{ + 1} - r_{ - 1} + 2\,r_{ + 3} - 2\,r_{ - 3} - r_{ + 4} + r_{ + 4} - r_{5} + r_{6} - j_{0} \, [ {\text{HIO]}}$$
(4)
$${\text{d}}\, [ {\text{HIO}}_{ 2} ] / {\text{d}}t = r_{ + 1} - r_{ - 1} - \,r_{2} + r_{6} + r_{8} - j_{0} \, [ {\text{HIO}}_{ 2} ]$$
(5)
$${\text{d}}\, [ {\text{I}}_{ 2} {\text{O]/d}}t = r_{2} - \,r_{ + 3} + \,r_{ - 3} - r_{6} - j_{0} \, [ {\text{I}}_{ 2} {\text{O]}}$$
(6)

Thus, we are dealing with the six-dimensional system, where under defined conditions, all six variables can be in the oscillatory dynamic states [8, 36].

Using the numerical integration of Eqs. 1–6, the time evolution as well as the dynamic states of the reaction system can be examined as a function of different control parameters such as concentrations of reactants and temperature.

Methods

For the numerical simulation of the time series obtained by one variant of the model of the BL oscillatory reaction under CSTR conditions, the MATLAB program package were used. The system of the ordinary differential equations was integrated using the ode15 s algorithm with variable step. In all simulations relative and absolute error tolerance values were 3 × 10−14 and 1 × 10−20, respectively.

For the method of numerical continuation, as discussed in our recently published paper [51] we developed a program in MATLAB programming package which perform 1-parameter and 2-parameter bifurcation analysis by using numerical continuation based on the pseudo-arc length scheme.

In simulations, initial concentration of iodate ions was 4.5 × 10−2 mol L−1, while the initial concentration of hydrogen ions was 6.4 × 10−2 mol L−1. The initial hydrogen peroxide concentration, set to be equal to inflow hydrogen peroxide concentration (h), was 4.0 × 10−2 mol dm−3. The initial concentration of intermediate species were: [I−]0 = 1.70 × 10−8 mol L−1, [HIO]0 = 9.20 × 10−8 mol L−1, [HIO2]0 = 3.20 × 10−7 mol L−1, [I2O]0 = 5.30 × 10−10 mol L−1 and [I2]0 = 1.00 × 10−5 mol L−1. The specific flow rate was j 0 = 0.007 min−1.

Experimental

The dynamic behavior of the BL reaction in a CSTR, was followed potentiometrically, using a Pt electrode (Model 6.0301.100, Metrohm, Herisau, Switzerland) and a double junction Ag/AgCl electrode (Model 6.0726.100, Metrohm, Herisau, Switzerland) as a reference. The temperature of the reaction mixture was maintained by a circulating water bath (Series U, MLW Freital, Germany) and controlled within ± 0.2 °C. Reagents of analytical grade (potassium iodate, sulfuric acid and hydrogen peroxide) were used as received and the solutions were prepared using deionized water (ρ = 18 MΩ cm, Milli−Q, Millipore, Bedford, MA, USA). Experimental details (reagents, apparatus and experimental procedures) are given in our previous publication [32]. In summary, we have examined BL dynamics in independent series of experiments in which the mixed inflow hydrogen peroxide concentrations and temperature were varied one at a time. In the experimental series described in this paper, the mixed inflow concentration of hydrogen peroxide, potassium iodate and sulfuric acid were: [H2O2]in = 0.040 mol L−1, [KIO3]in = 0.059 mol L−1 and [H2SO4]in = 0.055 mol L−1, whereas the specific flow rate was j 0 = 0.007 min−1. At this operation point, the temperature was varied in the range 41.5–55.0 °C and its influence on the BL dynamics was investigated. The effect of temperature was examined in both directions, for increasing and decreasing temperature values.

Results and discussion

For the simulation of controlled generation of various dynamic states (both periodic and aperiodic or chaotic) of the BL reaction system, the model of the reaction ought to be postulated, but it happens very often in the modelling procedure that the agreement between the experimental findings and the model predictions is not completely satisfactory. The unsuccessful simulation of experimentally obtained results opens the question: is the reaction model incorrect or the parameters are not well selected. In order to solve this difficult problem in the modelling procedure, we decided to correlate bifurcations, i.e. bifurcation points and bifurcation types obtained experimentally and numerically by the proposed model, using the temperature as the control parameter.

Under the considered experimental conditions, the bifurcation diagram (Fig. 1a) is obtained when the temperature is varied in the range of 41.5–55.0 °C. The transition from stable steady state to oscillatory dynamics is realized through supercritical Andronov–Hopf (SAH) bifurcation at the critical temperature value T SAH = 44.77 °C (Fig. 1b).

Fig. 1
figure 1

a A bifurcation diagram showing transition from the stable steady state (solid circle) to regular oscillations (open circles denoting minimal and maximal potential in an oscillation) when the temperature as a control parameter, was varied in the range of 41.5–55.0 °C. Experimental conditions: [H2O2]in = 0.040 mol L−1, [KIO3]in = 0.059 mol L−1, [H2SO4]in = 0.055 mol L−1, stirring rate o = 900 rpm and j 0 = 0.007 min−1. b Plot of the square of the oscillatory amplitude (A2) as a function of the temperature; the bifurcation point T SAH shows the characteristics of a supercritical Andronov–Hopf (SAH) bifurcation and occurs at T SAH = 44.77 °C

Full size image

For the numerical simulations of the BL reaction, we have chosen to work with a very simple variant of the model of the BL reaction realized under CSTR conditions given in “The model system” section (Table 1), which is able to simulate various dynamic states, such as simple or mixed-mode sustained oscillations and chaotic states. To this aim, the system of differential equations in Eqs. 1–6 together with related rate of all reaction and flow steps (R i ) and (f i ), respectively, denoted by r i , their rate constants k i at 60.0 °C 60 k i and values of activation energies E a,i [46, 47] were used (Table 2).

In the numerical simulations, we have applied conditions as similar as possible to the experimental ones. However, in experimental examinations, we had three species (hydrogen peroxide, potassium iodate and sulfuric acid) that flow through reactor with following inflow concentrations: [H2O2]in = 0.040 mol L−1, [KIO3]in = 0.059 mol L−1 and [H2SO4]in = 0.055 mol L−1, whereas in numerical simulations, it was only one species, that is hydrogen peroxide with inflow concentration of [H2O2]in = 0.040 mol L−1. In numerical simulations, the concentrations of potassium iodate and sulfuric acid were taken as constant, but, since we are dealing with weak acids, the effective concentrations of both hydrogen and iodate ions in the reaction mixture were recalculated by the procedure given in Ref. [52]. These concentrations are: [H+] = 5.9 × 10−2 mol L−1 and [IO3 −] = 6.4 × 10−2 mol L−1. In both cases, the specific flow rate was j 0 = 0.007 min−1.

The dynamic states obtained by the Eqs. 1–6 depend very much on the temperature as the control parameter. The temperature T is included in the rate constant of the ith reaction by the Arrhenius relation:

$$k_{i} = A_{i} \,e^{{ - \frac{{E_{i} }}{RT}}}$$
(7)

Here A i and E i are the Arrhenius constant and energy of activation of the ith reaction (given in Table 2.) respectively, whereas R is the gas constant. In numerical simulations, it is assumed that the Arrhenius constants A i are not functions of temperature. Hence, the rate constant at any temperature is calculated with respect to the one chosen for 60.0 °C. The rate constants at T = 60.0 °C, 60 k i , are given in Table 2.

The activation energies given in Table 2 have been selected in previous studies for better estimation of the activation energy of reaction (R3) as one of the most undefined parameter in the modelling of BL reaction [46, 47]. Here we use the same set of activation energies with the involvement of new variant of the kinetic model (R1–R6, R8) to simulate the experimentally observed unusual dependence of the reaction rate of iodine oxidation by hydrogen peroxide on the initial hydrogen peroxide concentration, at different temperatures aiming to test the capability of the model [18, 46]. Namely, in the batch reactor, if the system initially contained iodine, hydrogen peroxide and iodate in acidic media, iodine oxidation was observed to be first order with respect to iodine at the beginning of the reaction [46, 53]. With a change of the initial hydrogen peroxide concentration from higher to lower values, the corresponding iodine oxidation rates increased, reaching a maximum value and decrease afterwards with further lowering of the initial hydrogen peroxide concentration values. If applied in a batch reactor in the range of initial concentrations: [H+]0 = 0.0400 mol L−1, [IO3 −]0 = 0.0125 mol L−1, [I2]0 = 0.0002 mol L−1 and [H2O2]0 = 0.01−0.10 mol L−1 as in our experiments [46], the kinetic model variant involved here with parameters given in Table 2 has resulted with successful numerical simulation of the described changes in iodine oxidation initial rate at temperatures 60.00, 44.77 and 39.00 °C.

Nevertheless, the model with taken parameters (Table 2) could not simulate exactly the experimentally obtained bifurcation diagram under CSTR conditions given in Fig. 1. Namely, although the numerical simulation yields the same type of bifurcation (supercritical Andronov–Hopf, SAH), its position, related to experimental observation, is shifted towards higher temperature. This numerically observed bifurcation occurs at T SAH = 53.38 °C. Therefore, if we want to get the same position of bifurcation point as in the experiment, i.e. SAH at T SAH = 44.77 °C, we must change some of the model parameters. For this purpose, we decided to first change the value of activation energy of the third reaction (R3, Table 1) E a,3. Namely, just as we mentioned before, this parameter is one of the most undefined parameters of the model. Note that value of E a,3 was estimated 100 kJ mol−1 in publication [46]. Therefore, we examined whether and how to change the position of the SAH bifurcation if values of E a,3 are reduced from 100 kJ mol−1 to lower values. With that aim, we performed 2-parameter numerical continuation when the values of E a,3 and temperature were the continuation parameters. As a result, it appeared that SAH bifurcation at critical temperature, T SAH = 44.77 °C, could be obtained for two values of activation energy, which are 47.64 and 67.42 kJ mol−1 (Fig. 2). For these obtained values of activation energy, the corresponding bifurcation diagrams where temperature was varied from 41.0 to 55.0 °C are shown in Figs. 3a and 3b.

Fig. 2
figure 2

The position of the SAH bifurcation related to the value of activation energy of reaction (R3) E a,3 and temperature T, obtained by 2-parameter numerical continuation when the values of E a,3 and temperature were the continuation parameters. SAH bifurcation was obtained at critical temperature T SAH = 44.77 °C for two values of activation energies of reaction (R3) E a,3(A) = 47.64 kJ mol−1 and E a,3(B) = 67.42 kJ mol−1

Full size image
Fig. 3
figure 3

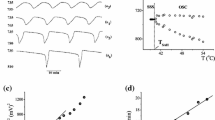
The bifurcation diagrams a and b obtained in points A and B (Fig. 2), respectively, that is for two values of activation energies of reaction (R3) E a,3(A) = 47.64 kJ mol−1 and E a,3(B) = 67.42 kJ mol−1. The bifurcation given in (b), is enlarged in (c) to show dynamic state with mixed-mode oscillations presented in (d) that appears closed to bifurcation point

Full size image

The SAH bifurcation is obtained only in the case presented at Fig. 3b, in other words for E a,3(B) = 67.42 kJ mol−1. However, close to the bifurcation point, the dynamic state with mixed-mode oscillations has been obtained (Figs. 3c and 3d), which is not case in experimental investigations (Fig. 1a). Hence, numerically and experimentally obtained bifurcation diagrams (Figs. 1a and 3b) are not equal; in the vicinity of numerically obtained critical temperature point, i.e. at 44.86 °C, the mixed-mode oscillations appear within which SAH bifurcation at 44.77 °C disappears at lower activation energies. Therefore, in the next step of the modelling procedure, for fine tuning of the considered model of the BL reaction, we decided to change another parameter, i.e. rate constant of the first reaction in the model, 60 k +1,0, in addition to the values of activation energy and temperature. However, at this point, we found different bifurcations related to both values of activation energies and rate constants of particular steps.

At this stage of analysis, for different values of activation energy of reaction (R3) E a,3, rate constant 60 k +1,0 is changed, aiming to obtain SAH bifurcation point, T SAH = 44.77 °C. In that way, we performed a 2-parameter analysis when the values of rate constant 60 k +1,0 and temperature were the continuation parameters. As a result, T SAH = 44.77 °C can be obtained for all examined activation energies until E a,3 = 85.00 kJ mol−1. Moreover, numerical analysis showed that the basic requirement that T SAH = 44.77 °C, for values of activation energy of 100.00 kJ mol−1, cannot be satisfied for any value of 60 k +1,0.

Thus, for example, model analysis with E a,3 = 85.00 kJ mol−1 shows that desired bifurcation point can be obtained for value of rate constant 60 k +1,0 equal to 1.13 × 105 M−3 min−1 (Fig. 4). For this obtained value of 60 k +1,0, the corresponding bifurcation diagram where temperature was varied from 41.00 to 55.00 °C is shown in Fig. 5.

Fig. 4
figure 4

The position of SAH bifurcation related to the rate constant of reaction (R1) 60 k +1,0 and temperature T. The large dot indicate value of 60 k +1,0 = 1.13 × 105 M−3 min−1 for which SAH bifurcation was obtained at critical temperature T SAH = 44.77 °C; E a,3 = 85.00 kJ mol−1

Full size image
Fig. 5
figure 5

Numerically obtained bifurcation diagram with temperature as a bifurcation parameter. E a,3 = 85.00 kJ mol−1, 60 k +1,0 = 1.13 × 105 M−3 min−1. The supercritical Andronov–Hopf bifurcation was obtained at critical temperature T SAH = 44.77 °C

Full size image

With the aim to see the relation between experimentally and numerically obtained results based on the model given in Table 1 as well as parameters given in Table 2, where only values of E a,3 = 100.00 kJ mol−1 is changed to E a,3 = 85.00 kJ mol−1 and 60 k +1,0 = 3.18 × 105 M−3 min−1 is changed to 60 k +1,0 = 1.13 × 105 M−3 min−1 (the case shown in Fig. 5), the periods between oscillations are presented in Fig. 6. Qualitative similarity was obtained, although the periods are more than two times longer in numerical simulations.

Fig. 6
figure 6

The periods between oscillations as a function of temperature in (a) Experimental investigations and (b) Numerical simulations based on the model given presented in Table 1 and parameters given in Table 2, where E a,3 = 85.00 kJ mol−1 and 60 k +1,0 = 1.13 × 105 M−3 min−1 (the case shown in Fig. 5)

Full size image

Finally, we should like to underline that the model with all examined combinations of values for 60 k +1,0 and E a,3 can simulate the above mentioned behavior of the system with respect to initial concentration of hydrogen peroxide and described in Refs. [46] and [47].

At the end, although in this paper, we did restrict our investigation to an examination of a model/bifurcation diagram sensitivity on the variation of both activation energy of reaction (R3), E a,3, and rate constant of reaction (R1), 60 k +1,0, there are great possibilities of selecting the unknown model parameters since the particular model studied in a CSTR has a large number of them. For useful modelling of the BL oscillatory reaction, the determination of the other activation energies and rate constants of model reaction steps is very important, that will be our target in the future.

In addition, the approach we used here led us to the procedure which could be generalized to any oscillatory reaction. It starts from an initial set of model parameters, which gives some oscillations but non-ideal agreement between simulation and experiment. The starting values of rate constants and activation energies would ideally be obtained from independent kinetic measurement, but, since it is rarely possible to realize, several of them will usually be obtained including certain level of more or less qualified scientific guess. The least reliable parameters should be identified and adjusted in further steps. As the first step, from numerical simulations, we construct the bifurcation diagram to compare numerically obtained results with experimental ones. The bifurcation point and bifurcation type must be identified. Then we use a two-parameter numerical continuation of the bifurcation point, where one of the parameters is the same control parameter as the one from the experiment, and the other is the least reliable model-parameter. If there are several unknown parameters to choose among, prior stability analysis would be useful to identify those who significantly influence the instability of the steady state. As a result of the continuation, the set of parameter values could be identified that produce satisfying agreement between the experimental and numerical bifurcation points. Furthermore, numerical simulations are necessary to determine the bifurcation type fully in each identified bifurcation point. Among appropriate bifurcation points, ones that have the same type as identified in the experiment will be chosen. Also, other qualitative (oscillations type and dynamical structure type) or quantitative (oscillatory amplitude, period, etc.) properties of the obtained dynamic states could be used to refine the kinetic parameters of the model further. For this purpose, two-parameter numerical continuation is performed like before, but for several values of newly selected kinetic parameters. The procedure can be repeated in the same way for several parameters. Namely, the proposed procedure for the examination of the postulated model validity based on synchronization of bifurcation diagrams obtained experimentally and numerically, taking care about qualitative and quantitative characteristics of this bifurcation as well as its position in the space of parameters, can be applied to any oscillatory reaction.

Conclusion

In this paper, we have tried to answer the question: why we cannot simulate all the experimentally obtained phenomena perfectly by the considered variant of the BL reaction model—whether it is due to incorrect model or the possibility that undefined model parameters were not well selected. The considered reaction model is already published minimal variant of the BL reaction, which is able to qualitatively describe almost all dynamical features of BL oscillator (either regular and mixed-mode oscillations or chaos). Thus, starting from already published set of model parameters, we numerically simulated an experimentally obtained bifurcation diagram. For fine-tuning between experimental and numerical results, the selected unknown model parameters, such as values of activation energy and rate constant of particular step that exist in the considered reaction model, were varied. In that way, 2-parameter numerical continuations when the model parameter (both values of activation energy of third model reaction E a,3 and rate constant of first model reaction 60 k +1,0) and temperature were the continuation parameters.

From our results, it is obvious that the considered variant of the model of the BL oscillating reaction is able to show the appropriate type of bifurcation, as well as to “move” bifurcation to the desired point in the phase space. Despite the fact that we can adapt the appearance of bifurcation diagrams, we have not succeeded to combine all the effects with new set of model parameters where only values of two parameters that are activation energy of third model reaction E a,3 and rate constant of first model reaction 60 k +1,0 were changed. For example, at present, the periods found between oscillations in vicinity of considered bifurcation were more than two times longer than it should be. Therefore, a further analysis of the sensitivity of the model on other parameters is necessary. In this sense, although the obtained results where only two parameters were changed (E a,3 and 60 k +1,0) were very promising, in the present stage of examinations, we cannot give a definitive answer to the question whether a full agreement can be obtained by changing the model unknown parameters or the reaction model itself has to be modified. Moreover, an unambiguous explanation and a definitive answer are difficult to give because there are great possibilities of changing these parameters and their combinations. However, the proposed approach can be a guideline for further model harmonization.