Skip to main content
SpringerLink
Log in

Self-Action of Ultrashort Pulses in the Self-Similar Regime

  • Published:
Radiophysics and Quantum Electronics Aims and scope

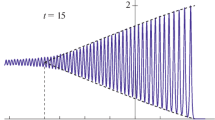
We study the specific features of the evolution of spatially confined pulses with a finite amplitude and a duration of several periods of wave field oscillations both analytically and numerically. The initial equation, which describes propagation of a reflectionless ultrashort pulse, is transformed to a nonautonomous modified Korteveg-de-Vries equation after passing over to self-similar variables. In this simpler equation for the self-similar function, the dynamics of the internal structure of the wave field is determined by the competition of “dispersion” and cubic nonlinearity only. The evolution of pulses in the directions of the increasing and decreasing nonlinearity is separately considered. Numerical simulation of the problem has demonstrated that: i) the energy center of the wave packet moves nonuniformly along the propagation path, ii) a dispersion shock wave consisting of a set of solitons is excited in the rear part of a pulse propagating in the direction of increasing nonlinearity in the process of the dispersion spreading, and iii) the evolution of the pulses propagating in the direction of decreasing nonlinearity is also accompanied by excitation of a breather soliton.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. G. Z. Gareev and V.V. Luchinin, Terahertz System and Technologies (State-of-the-Art Review) [in Russian], Saint Petersburg Electrotechnical University "LETI," St. Petersburg (2015).

  2. V. L. Bratman, A. G. Litvak, and E. V. Suvorov, Phys. Usp., 54, 837–844 (2011). https://doi.org/https://doi.org/10.3367/UFNe.0181.201108f.0867

  3. Th.Brabec and F. Krausz, Phys. Rev. Lett., 78, No. 17, 3282–3285 (1997). https://doi.org/https://doi.org/10.1103/PhysRevLett.78.3282

  4. E. A. Khazanov, S.Yu. Mironov, and G.Mourou, Phys. Usp., 62, 1096–1124 (2019). https://doi.org/https://doi.org/10.3367/UFNe.2019.05.038564

  5. S.A.Akhmanov, V.A.Vysloukh, and A. S.Chirkin, Optics of Femtosecond LaserPulses, AIP, New York (1992).

    Google Scholar 

  6. E. M. Gromov and V. I.Talanov, J. Exp. Theor. Phys., 83, No. 1, 73–79 (1996).

    ADS  Google Scholar 

  7. E. M. Belenov and A. V. Nazarkin, JETP Lett., 53, No. 4, 200–203 (1991).

    ADS  Google Scholar 

  8. V. A. Mironov, J. Exp. Theor. Phys., 89, 18–23 (1999). https://doi.org/https://doi.org/10.1134/1.558949

  9. S. A.Kozlov and S.V. Sazonov, J. Exp. Theor. Phys., 84, No. 2, 221–228 (1997). https://doi.org/https://doi.org/10.1134/1.558269

  10. A. N. Berkovsky, S. A.Kozlov, and Y. A. Shpolyansky, Phys. Rev. A, 72, No. 4, 043821. https://doi.org/https://doi.org/10.1103/PhysRevA.72.043821

  11. M. I.Rabinovich an D.N.Trubetskov, Oscillations and Waves: In Linear and Nonlinear Systems (Mathematics and Its Applications), Springer, Berlin (1989).

  12. V. S. L’vov, Nonlinear Spin Waves [in Russian], Nauka, Moscow (1987).

    Google Scholar 

  13. A. A. Balakin, A. G. Litvak, V.A.Mironov, and S. A. Skobelev, J. Exp. Theor. Phys., 104, 363–378 (2007). https://doi.org/https://doi.org/10.1134/S106377610703003X

  14. G. I. Barenblatt, Similarity, Self-Similarity, Intermediate Asymptotics [in Russian], Gidrometeoizdat, Leningrad (1982).

    MATH  Google Scholar 

  15. O.V.Rudenko and O.A. Sapozhnikov, Phys. Usp., 47, 907–922 (2004). https://doi.org/https://doi.org/10.1070/PU2004v047n09ABEH001865

  16. A. V.Ovsyannikov, Group Analysis of Differential Equations, Academic Press (2014).

  17. N. Kh. Ibragimov, Practical Course of Differential Equations and Mathematical Modeling [in Russian], N. I. Lobachevsky State University of Nizhny Novgorod (2007).

  18. E. M. Lifshitz and L.P.Pitaevskii, Physical Kinetics: Vol. 10, Elsevier Science (1995).

  19. A. M. Kamchatnov, Phys. Usp., 64, 48–82 (2021). https://doi.org/https://doi.org/10.3367/UFNe.2020.08.038815

  20. M.A. Shamsutdinov, I.Yu. Lomakina, V.N.Nazarov et al., Ferro- and Antiferrodynamics. Nonlinear Oscillations, Waves, and Solitons [in Russian], Nauka, Moscow (2009).

Download references

Author information

Authors and Affiliations

  1. Institute of Applied Physics of the Russian Academy of Sciences, Nizhny Novgorod, Russia

    V. A. Mironov & D. A. Fadeev

Authors
  1. V. A. Mironov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. D. A. Fadeev
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to D. A. Fadeev.

Additional information

Translated from Izvestiya Vysshikh Uchebnykh Zavedenii, Radiofizika, Vol. 65, No. 1, pp. 35–45, January 2022. Russian DOI: https://doi.org/10.52452/00213462_2022_65_01_35

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mironov, V.A., Fadeev, D.A. Self-Action of Ultrashort Pulses in the Self-Similar Regime. Radiophys Quantum El 65, 32–41 (2022). https://doi.org/10.1007/s11141-022-10191-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11141-022-10191-2

Search

Navigation