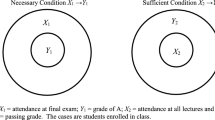
Abstract
Ragin’s Qualitative Comparative Analysis (QCA) and related set theoretic methods are increasingly popular. This is a welcome development, since it encourages systematic configurational analyses of social phenomena. One downside of this growth in popularity is a tendency for more researchers to use the approach in a formulaic manner—something made possible, and more likely, by the availability of free software. We wish to see QCA employed, as Ragin intended, in a self-critical manner. For this to happen, researchers need to understand more of what is going on behind the results generated by the available software packages. One important aspect of set theoretic analyses of sufficiency and necessity is the effect that the distribution of cases in a dataset can have on results. We explore this issue in a number of ways. We begin by exploring how both deterministic and nondeterministic data-generating processes are reflected in the analyses of populations differing in only the weights of types of cases. We show how and why weights matter in causal analyses that focus on necessity and also, where models are not fully specified, sufficiency. We then draw on this discussion to show that a recent textbook discussion of hidden necessary conditions is weakened as a result of its neglect of weighting issues. Finally, having shown that case weights raise a number of difficulties for set theoretic analyses, we offer suggestions, drawing on two imagined population datasets concerning health outcomes, for mitigating their effect.





Similar content being viewed by others
Notes
We are assuming, to keep things simpler, that the causal relations between S, T and O are not a function of the distributions of the possible configurations of the two conditions S and T and their negations in the populations. In fact, they often will be: in cases, for example, where the configurations are real actors in conflict over positional goods. We are also bracketing out here any causal analysis of the origin of the pattern of weights in a truth table. Clearly there are causes behind the weight of cases in a population. Wars would affect, via migration, the weights of ethnic groups, for example. Birth rates—and their causes—would affect the weights of children in social classes. Random processes will affect weights in samples from populations. These matters are clearly also important, but not our concern here.
This non-minimised relation also reminds us that, as Baumgartner (2008) notes, as long as there are at least two terms on the left-hand side, there is an asymmetry between sufficiency and necessity. It makes sense to think of causal influences running from left to right, but not from right to left, since knowing O does not tell us which of the two left-hand side terms are present.
As long as they each are above zero and we have adequate evidence for the implication claims 1–4.
The crucial issue here is the ratio of A to C, not the absolute sizes of A or C.
This fictitious structure, for our current purposes, is best seen as incorporating a random element (as in, e.g., ST causes the probability of gaining the outcome to be 0.99). It would also be possible to see it as having omitted some relevant causal factor but, given the ways in which imperfect model specification can also affect the assessment of sufficiency (see Sect. 2 and what follows in this section), this possible account of it is best avoided in this paper.
Again, we are assuming, to keep things simpler, that the causal relations between S, T and O are not a function of the distributions of the configurations in the populations (see footnote 1).
It is perhaps important to note that our arguments do not depend on the particular threshold (0.8) employed. Given appropriate case weights and/or postulated causal structures, the problems we discuss could also appear with stricter thresholds such as 0.9.
We will not discuss samples from populations in this paper, but clearly much of what we write has implications for the use of QCA with samples, especially where some cases are more or less represented than others via sampling (see Glaesser and Cooper 2012). We should also note, concerning populations, that sometimes there will be only one population. Some implications of this for the analysis of necessity are considered in Sect. 5.
Personal communication (email), 10/11/14.
Personal communication (email), 10/11/14.
Cooper et al. (2014) also provide a critical discussion of Schneider and Wagemann’s arguments and proposals re the treatment of necessary conditions given limited diversity.
45 of the 49 cases with the outcome Y have the condition \(\sim \)B.
Note that the coverage index for the necessity of \(\sim \)B (i.e., the extent to which \(\sim \)B is sufficient for the outcome) remains at 0.978 (=45/46) for every point on both graphs. This is because the cases in row 7 are irrelevant to its calculation.
In the case of sufficiency, our earlier discussion has shown the importance of having correct knowledge of causes.
The treatment of trivialness/relevance as a single scale (where relevance indicates non-trivialness) differentiates their approach from that of Goertz. For him, relevance parallels Ragin’s coverage, i.e., the degree to which a necessary condition is also sufficient. See footnote 12 on p. 237 of their book.
This is \(\mathrm{SUM}(1-\mathrm{X}_\mathrm{i})/\mathrm{SUM}(1-\mathrm{MIN}(\mathrm{X}_\mathrm{i},\,\mathrm{Y}_\mathrm{i})).\) The key point here is that cases in the X, Y cell of a \(2\times 2\) table contribute nothing to the summation. Schneider and Wagemann (2012) argue that their formula picks up a source of trivialness missed by Ragin’s coverage measure.
Since, comparing Tables 8 and 9, the 12 in the \(\sim \)X, \(\sim \)Y cell in Table 9 forms a smaller proportion of the total cases, we might perhaps argue that the problem of a potentially trivial necessary condition X is greater for this second population—in the sense that this cell is nearer the zero that would indicate trivialness for Goertz (2006).
This may not be the case in practice.
This result is not sensitive to rescaling the tables so that they have the same total population.
More precisely, 11.89.
The coverage of \(\sim \)X for \(\sim \)Y is also much higher for society D than for society E: 0.980 versus 0.324. In Ragin’s terms, \(\sim \)X has more empirical importance for ill health in society D than E, even though the (probabilistic) causal consequences of \(\sim \)X for any individual remain the same.
Ragin’s (2008) truth table algorithm behaves similarly, in the analysis of sufficiency, in the way it minimises a truth table.
Beyond there being enough to warrant the causal claims.
Baumgartner, in his very important work on CNA—a configurational method that uses an alternative minimisation algorithm to that employed in QCA—tends in his more fundamental papers effectively to assume one case per row (e.g., Baumgartner 2013, 2014). However, in his application, with Epple, of CNA to the case of the Swiss minarets referendum (Baumgartner and Epple 2014) this approach is combined with one that takes account of case numbers when calculating coverage, etc.
References
Baumgartner, M.: Regularity theories reassessed. Philosophia 36, 327–354 (2008)
Baumgartner, M.: Detecting causal chains in small-n data. Field Methods 25, 3–24 (2013)
Baumgartner, M.: Parsimony and causality. Qual. Quant. (2014). doi:10.1007/s11135-014-0026-7
Baumgartner, M., Epple, R.: A coincidence analysis of a causal chain: the Swiss minaret vote. Sociol. Methods Res. 43, 280–312 (2014)
Bhaskar, R.: A Realist Theory of Science. Harvester, Brighton (1975)
Bhaskar, R.: The Possibility of Naturalism. Harvester, Brighton (1979)
Cooper, B.: Applying Ragin’s crisp and fuzzy set QCA to large datasets: social class and educational achievement in the National Child Development Study. Sociol. Res. Online 10(2) (2005). http://www.socresonline.org.uk/10/2/cooper1.html
Cooper, B., Glaesser, J.: Paradoxes and pitfalls in using fuzzy set QCA: illustrations from a critical review of a study of educational inequality. Sociol. Res. Online 16(3) (2011). http://www.socresonline.org.uk/16/3/8.html
Cooper, B., Glaesser, J.: Qualitative work and the testing and development of theory: lessons from a study combining cross-case and within-case analysis via Ragin’s QCA. Forum: Qualitative Social Research/Qualitative Sozialforschung. 13(2), Art. 4 (2012). http://www.qualitative-research.net/index.php/fqs/article/view/1776
Cooper, B., Glaesser, J., Thomson, S.: Schneider and Wagemann’s proposed enhanced standard analysis for Ragin’s Qualitative Comparative Analysis: some unresolved problems and some suggestions for addressing them. COMPASSS WP Series 2014–77 (2014). http://www.compasss.org/wpseries/CooperGlaesserThomson2014.pdf
Gerring, J.: Social Science Methodology: A Unified Framework, 2nd edn. Cambridge University Press, Cambridge (2012)
Glaesser, J., Cooper, B.: Gender, parental education, and ability: their interacting roles in predicting GCSE success. Camb. J. Educ. 42(4):463–480 (2012)
Goertz, G.: Assessing the trivialness, relevance, and relative importance of necessary or sufficient conditions in social science. Stud. Comp. Int. Dev. 41, 88–109 (2006)
Pawson, R.: A Measure for Measures: A Manifesto for Empirical Sociology. Routledge and Kegan Paul, London (1989)
Ragin, C.C.: The Comparative Method. Moving Beyond Qualitative and Quantitative Strategies. University of California Press, Berkeley (1987)
Ragin, C.C.: Fuzzy-Set Social Science. University of Chicago Press, Chicago (2000)
Ragin, C.C.: Set relations in social research: evaluating their consistency and coverage. Polit. Anal. 14(3), 291–310 (2006)
Ragin, C.C.: Redesigning Social Inquiry: Fuzzy Sets and Beyond. University of Chicago Press, Chicago (2008)
Schneider, C.Q., Wagemann, C.: Set-Theoretic Methods for the Social Sciences. A Guide to Qualitative Comparative Analysis. Cambridge University Press, Cambridge (2012)
Acknowledgments
This work has been supported by the UK’s Economic and Social Research Council. Thanks to the four Q&Q reviewers for their very helpful comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cooper, B., Glaesser, J. Analysing necessity and sufficiency with Qualitative Comparative Analysis: how do results vary as case weights change?. Qual Quant 50, 327–346 (2016). https://doi.org/10.1007/s11135-014-0151-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11135-014-0151-3