Diffusion of innovations in dense and sparse networks

Abstract

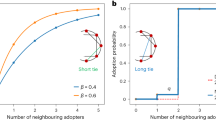
This paper puts forward a comparison of the performance of sparsely and densely connected social networks in promoting the diffusion of innovations of uncertain profitability. To this end, we use a threshold model of innovation diffusion, based on a classic model of adoption of innovations via imitation by Jensen (Int. J. Ind. Organ. 6:335–350, 1988), to evaluate the probability of diffusion of an innovation in three classes of networks: the circular, the star-shaped and the complete networks. We find that, if agents hold a low prior confidence in the profitability of an innovation, then complete networks and star networks with informed agents (i.e., with agents who are aware of the structure of the network and use this information rationally) perform better than circles and than stars with myopic agents. The converse is true for innovations accompanied by initial high expectations about their profitability.

Appendix

Proof (of lemma 2)

Point i): Recall that, by definition, $\overline{p}_{0}$ is such that for all $p_{0}\ge$ $\overline{p}_{0},$ $h(1,n-1,p_{0})\ge p^{*}(n-1)$ and that $h(.)$ monotonically grows in $p_{0}.$ Since $h(1,1,p_{0})>h(1,n-1,p_{0}),$ then there exists a $\widehat{p}_{0}<\overline{ p}_{0}$ s. t. $h(1,1,p_{0})>p^{*}(1)$ for all $p_{0}>\widehat{p}_{0},$ and vice versa. Point ii): Recall that $\underline{p}_{0}$ is s. t. $h(n-1,n-1,p_{0})\le p^{*}(n-1)$ for all $p_{0}<\underline{p}_{0}$ and that $h(.)$ monotonically grows in $p_{0}.$ Then, since $h(n-1,n-1,p_{0})>h(1,1,p_{0}),$ such a $\widehat{p}_{0}$ must be strictly larger than $\underline{p}_{0}$. $\square$

Proof (of proposition 3)

It follows from lemma 2. $\square$

Proof (of corollary 4)

It follows from proposition 3. $\square$

Proof (of lemma 5)

Recall that $\underline{p}_{0}$ is such that $h(k,n-1,p_{0})=p^{*}(n-1)$ for $k=n-1$ and $p_{0}=\underline{p}_{0},$ and note that $h(k,n-1,p_{0})$ monotonically grows in $p_{0}$ and in $k.$ It follows that for any $p_{0}\ge$ $\underline{p}_{0}$ there exists an integer $k\in [2,n-1]$ such that $h(k,n-1,p_{0})\ge p^{*}(n-1)$. $\square$

Proof (of proposition 6)

It follows from the definition of the threshold integer $k$ and from the fact that, in a complete network, all agents observe $n-1$ other agents. $\square$

Proof (of corollary 7)

It follows from proposition 6. $\square$

Proof (of proposition 8)

Myopic agents do not take into account the size of the sample observed by the central node. Thus, they observe the choice of just one agent and their adoption threshold is $p^{*}(1).$ Therefore: point (i) follows from the definition of $\widehat{p}_{0};\$and point (ii) stems form the fact that the center adopts the innovation upon the occurrence of the union of two events: $(x_{c}\in E)\cup (a\ge k(p_{0})).$ The probability that either of these two non independent events occurs, $\Pr \left[ (x_{c}\in E)\cup (a\ge k(p_{0}))\right] ,$ is equal to

$$\begin{aligned}&\sum _{a=k}^{n}\left( {\begin{array}{c}n\\ a\end{array}}\right) \pi ^{a}(1-\pi )^{n-a}+\pi -\pi \sum _{a=k}^{n} \left( {\begin{array}{c}n\\ a\end{array}}\right) \pi ^{a}(1-\pi )^{n-a} \\&= \sum _{a=k}^{n}\left( {\begin{array}{c}n\\ a\end{array}}\right) \pi ^{a}(1-\pi )^{n-a}+\pi \left[ 1-\sum _{a=k}^{n}\left( {\begin{array}{c}n\\ a\end{array}}\right) \pi ^{a}(1-\pi )^{n-a}\right] \\&= \sum _{a=k}^{n}\left( {\begin{array}{c}n\\ a\end{array}}\right) \pi ^{a}(1-\pi )^{n-a}+\pi \sum _{a=1}^{k-1} \left( {\begin{array}{c}n\\ a\end{array}}\right) \pi ^{a}(1-\pi )^{n-a} \end{aligned}$$

$\square$

Proof (of corollary 9)

Rational peripheral agents take into consideration the size of the sample observed by the central node and know that they all share the same prior belief $p_{0}$. Thus, the observation of the behaviour of the central node at date 2 reveals to all peripheral agents whether $a\ge$ $k(p_{0})$ or not. Therefore, the signal that they receive at date 2 informs them about the behaviour of $n-1$ agents (the center plus the other $n-2$ peripheral agents), i.e. $v=n-1$ and, consequently, $p^{*}(v)=p^{*}(n-1)$ for all informed peripheral agents in a star network. It follows that such agents adopt via imitation if they observe the joint occurrence of two events: $(x_{c}\notin E)\cap (a\ge$ $k(p_{0})).$ The probability that such a state of the world takes place is

$$\begin{aligned} \Pr \left[ (x_{c}\notin E)\cap (a\ge k(p_{0}))\right] =(1-\pi )\sum _{a=k}^{n}\left( {\begin{array}{c}n\\ a\end{array}}\right) \pi ^{a}(1-\pi )^{n-a} \end{aligned}$$

$\square$