Appointment-driven queueing systems with non-punctual customers

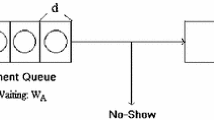
Abstract

We consider a single-server queueing system where a finite number of customers arrive over time to receive service. Arrivals are driven by appointments, with a scheduled appointment time associated with each customer. However, customers are not necessarily punctual and may arrive either earlier or later than their scheduled appointment times or may not show up at all. Arrival times relative to scheduled appointments are random. Customers are not homogeneous in their punctuality and show-up behavior. The time between consecutive appointments is allowed to vary from customer to customer. Moreover, service times are assumed to be random with a $\gamma$-Cox distribution, a class of phase-type distributions known to be dense in the field of positive distributions. We develop both exact and approximate approaches for characterizing the distribution of the number of customers seen by each arrival. We show how this can be used to obtain the distribution of waiting time for each customer. We prove that the approximation provides an upper bound for the expected customer waiting time when non-punctuality is uniformly distributed. We also examine the impact of non-punctuality on system performance. In particular, we prove that non-punctuality deteriorates waiting time performance regardless of the distribution of non-punctuality. In addition, we illustrate how our approach can be used to support individualized appointment scheduling.

Appendices

Appendix A: Triangular distribution for punctuality

Consider the case where customer non-punctuality is homogeneous and follows a symmetric triangular distribution. For $1 \le n \le M$, we have

$$\begin{aligned} f_n(x)= {\left\{ \begin{array}{ll} \frac{(x-d_n+\tau )}{\tau ^2}, &{} \quad \text {if } d_n-\tau \le x < d_n, \\ \frac{(d_n+\tau -x)}{\tau ^2}, &{} \quad \text {if } d_n \le x \le d_n+\tau , \\ 0, &{} \quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

(39)

Similarly to the uniform distribution case, we calculate $p_{2,1}$ to complete the initialization step, since we have $f_1(t)$ from the definition of $f_n(t)$ and $p_{2,0} = 1 - p_{2,1}$. Here, we have $\displaystyle \text{ Pr }\{D_1<d_1\}= \text{ Pr }\{D_1\ge d_1\}= \frac{1}{2}$. When customer 1 arrives before $d_1$, we have

$$\begin{aligned} p_{2,1|D_1<d_1}&=\int _{d_2-d_1-\tau }^{d_2-d_1+\tau } e^{-\mu x} f_2(x+d_1)\,\mathrm{d}x \nonumber \\&=\int _{d_2-d_1-\tau }^{d_2-d_1} e^{-\mu x} \frac{(x+d_1-d_2+\tau )}{\tau ^2}\,\mathrm{d}x\nonumber \\&\quad + \int _{d_2-d_1}^{d_2-d_1+\tau } e^{-\mu x} \frac{(d_2+\tau -x-d_1)}{\tau ^2}\,\mathrm{d}x \nonumber \\&= \frac{\left( e^{\mu \tau }-1\right) ^2 e^{-\mu \left( -d_1+d_2+\tau \right) }}{\mu ^2 \tau ^2}. \end{aligned}$$

(40)

To derive $p_{2,1|D_1>d_1}$, we first compute $h_{2,1|D_1 \ge d_1}(x)$, the pdf of the random variable $D_2-D_1 | D_1 \ge d_1$. Using (7), we can compute $h_{1|D_1 \ge d_1}(x)$ on $[d_2-d_1-\tau _2^l-\tau _1^u, d_2-d_1+\tau _2^u]$ as

(41)

where $C_\mathrm{min} = \min \{\tau , d_2-d_1-x\}$ and $D_\mathrm{min} = \min \{\tau , d_1+\tau +x - d_2\}$. By substituting $h_{1|D_1 \ge d_1}(x)$ in Eq. (4) by (41), we obtain

$$\begin{aligned} p_{2,1|D_1\ge d_1}&= \int _{d_2-d_1-\tau _2^l-\tau _1^u}^{d_2-d_1+\tau _2^u} e^{-\mu x}h_{1|D_1 \ge d_1}(x)\,\mathrm{d}x\nonumber \\&= \int _{d_2-d_1-\tau _2^l-\tau _1^u}^{d_2-d_1} e^{-\mu x} C_\mathrm{min}\left( \tau _1^u + \frac{(C_\mathrm{min})^2}{6\tau _2^l} -\frac{\tau _1^u C_\mathrm{min}}{2\tau _2^l} - \frac{1}{2}(d_2-d_1-x) \right) \,\mathrm{d}x \nonumber \\&\quad + \int _{d_2-d_1-\tau _1^u}^{d_2-d_1+\tau _2^u} e^{-\mu x} D_\mathrm{min} \left( \frac{1}{2} (x+d_1-d_2+\tau _1^u) - \frac{1}{6\tau _2^u}{D_\mathrm{min}}^2\right) \,\mathrm{d}x\nonumber \\&= -\frac{\left( \mu ^2 \tau ^2 e^{3 \mu \tau } (2 \mu \tau -3)+\mu ^2 \tau ^2 (5 \mu \tau +3)+12 e^{2 \mu \tau }-6 e^{\mu \tau } (\mu \tau (\mu \tau +2)+2)\right) e^{-\mu \left( -d_1+d_2+\tau \right) }}{3 \mu ^4 \tau ^4}. \end{aligned}$$

(42)

With (40) and (42), we complete the initialization step by computing $p_{2,1}$ as

$$\begin{aligned} p_{2,1}&=\alpha _1 \text{ Pr }\{D_1<d_1\} p_{2,1|D_1<d_1} + \alpha _1 \text{ Pr }\{D_1\ge d_1\} p_{2,1|D_1\ge d_1}\\&=\frac{\alpha _1\left( -5 \mu ^3 \tau ^3-\mu ^2 \tau ^2 e^{3 \mu \tau } (2 \mu \tau -3)+3 e^{2 \mu \tau } \left( \mu ^2 \tau ^2-4\right) +12 e^{\mu \tau } (\mu \tau +1)\right) e^{-\mu \left( -d_1+d_2+\tau \right) }}{6 \mu ^4 \tau ^4}. \end{aligned}$$

Appendix B: Details for the analysis of $\gamma$-Cox-distributed service times

The moments of the waiting time can be obtained similarly to the exponential service time case. We have

$$\begin{aligned} {\mathbb {E}}[W_n^k]=\sum _{r=1}^{(n-1)m} p_{n,r} {\mathbb {E}}[W_{n,r}^k], \end{aligned}$$

(43)

for $2\le n \le M$, where $W_{n,r}$ is the random variable denoting the waiting time in the queue of customer n, given that customer n shows up and finds r actual phases of service in system remain to be serviced (i.e., the system state $R_n$ is r). Since service times follows independent $\gamma$-Cox distribution with m phases, the completion time of each phase is independently and exponentially distributed with rate $\gamma$. Therefore, $W_{n,r}$ has an r-Erlang distribution with r phases and rate $\gamma$ per phase. Using Eq. (43) and knowing that $\displaystyle {{\mathbb {E}}[W_{n,r}]= \frac{r}{\gamma }}$ and $\displaystyle {{\mathbb {E}}[W_{n,r}^2]=\frac{r(r+1)}{\gamma ^2}}$, we obtain

$$\begin{aligned} {\mathbb {E}}[W_n]=\sum _{r=1}^{(n-1)m} p_{n,r} \frac{r}{\gamma }\text { and } {\mathbb {E}}[W_n^2]=\sum _{r=1}^{(n-1)m} p_{n,r} \frac{r(r+1)}{\gamma ^2}, \end{aligned}$$

(44)

for $2\le n \le M$. Moreover, we have

$$\begin{aligned} \text{ Pr }\{W_{n,r}<t\}=1-\sum _{j=0}^{r-1} \frac{(\gamma t)^j}{j!}\,e^{-\gamma t}, \end{aligned}$$

(45)

for $t\ge 0$. Consequently,

$$\begin{aligned} \text{ Pr }\{W_n<t\}&=p_{n,0} + \sum _{r=1}^{(n-1)m} p_{n,r} \text{ Pr }\{W_{n,r}<t\}\nonumber \\&=1-\sum _{r=1}^{(n-1)m} \sum _{j=0}^{r-1} p_{n,r} \frac{(\gamma t)^j}{j!}\,e^{-\gamma t}. \end{aligned}$$

(46)

The case $n=1$ is treated separately. The moments and distribution of the first customer’s waiting time can be obtained exactly the same as for the exponential case, using Eqs. (19)–(21).

Appendix C: Proof of Propositions

1.1 Proof of Proposition 1

We first state several definitions and lemmas that will be used in the proof. We denote by $S_n$ the random variable of the service time of customer n, and by $A_n$ the random variable for the arrival time of customer n. For a given schedule $\delta = (d_1, d_2, \ldots , d_M)$, we have $A_n = D_n$ if customer n is not punctual, and $A_n = {\mathbb {E}}[D_n]$ if customer n is punctual.

We use $\gamma _n \in \{0, 1\}$ to denote the type of punctuality of customer n, where $\gamma _n = 0$ if customer n arrives with non-punctuality at time $D_n \in [d_n - \tau _n^l, d_n + \tau _n^u]$, and $\gamma _n = 1$ if customer n arrives with punctuality at time ${\mathbb {E}}[D_n]$. Let us denote by $\Gamma = (\gamma _1, \ldots , \gamma _M)$ the customer’s punctuality profile and use $A_n(\Gamma )$, $W_n(\Gamma )$, and $C_n(\Gamma )$ to represent the arrival, waiting, and completion time of customer n under the profile $\Gamma$, where $A_n(\Gamma ) = D_n$ if $\gamma _n = 0$, and $A_n(\Gamma ) = {\mathbb {E}}[D_n]$ if $\gamma _n = 1$. For $0 \le k \le M$, let $\Gamma _k$ denote the profile where the first k customers are punctual and the last $M-k$ customers are non-punctual.

For $a_k, s_k \in {\mathbb {R}}$, let $\mathbf {a}_k = (a_1, \ldots , a_k)$, and $\mathbf {s}_k= (s_1, \ldots , s_k)$. For $k = 0, \ldots , M$, we define the function $h_k(\mathbf {a}_k,\mathbf {s}_k)$ $:{\mathbb {R}}^{2k} \rightarrow {\mathbb {R}}$ as follows:

$$\begin{aligned} h_0(\mathbf {a}_0,\mathbf {s}_0)&= h_0 = d_1, \\ h_k(\mathbf {a}_k,\mathbf {s}_k)&= \max (h_{k-1}(\mathbf {a}_{k-1},\mathbf {s}_{k-1}), a_k) + s_k \quad \text {for } k = 1,\ldots , M. \end{aligned}$$

Proposition 4

For $k \in \{1, \ldots , M\}$, $h_n(\mathbf {a}_n,\mathbf {s}_n)$ is convex with respect to $a_k$ for $k \le n \le M$.

Proof

First, note that the function $h_{k-1}(\mathbf {a}_{k-1},\mathbf {s}_{k-1})$ only relies on the first $k-1$ elements of $\mathbf {a}_n$ and $\mathbf {s}_n$, and is constant with respect to $a_l$ and $s_l$, for $l \ge k$. From standard results, we know that $\max (C,f(x))$ is convex in x if f(x) is convex in x and C is constant with respect to x. It is then easy to see that $h_k(\mathbf {a}_k,\mathbf {s}_k) = \max (h_{k-1}(\mathbf {a}_{k-1},\mathbf {s}_{k-1}), a_k) + s_k$ is convex in $a_k$. Let us consider $n > k$ and assume that $h_{n-1}(\mathbf {a}_{n-1},\mathbf {s}_{n-1})$ is convex in $a_k$. Again, we can see that $h_{n}(\mathbf {a}_{n},\mathbf {s}_{n}) = \max (h_{n-1}(\mathbf {a}_{n-1},\mathbf {s}_{n-1}), a_{n}) + s_{m+1}$ is convex in $a_k$. Therefore, by induction, we have shown that $h_n(\mathbf {a}_{n},\mathbf {s}_{n})$ is convex in $a_k$ for all $n \ge k$, which finishes the proof of the proposition. $\square$

For $1 \le k \le n \le M$, we define the functions $g_{n,k}$ and ${\hat{g}}_{n,k}: {\mathbb {R}}^{2n-2} \rightarrow {\mathbb {R}}$ as follows: If $n=k$,

$$\begin{aligned}&g_{k,k}((a_1, \ldots , a_{k-1}), \mathbf {s}_{k-1})= {\mathbb {E}} [(h_{k-1} ((a_1, \ldots ,a_{k-1}), \mathbf {s}_{k-1}) - D_k)^+ ], \\&\qquad {\hat{g}}_{k,k}((a_1, \ldots , a_{k-1}), \mathbf {s}_{k-1}) = (h_{k-1} ((a_1, \ldots ,a_{k-1}), \mathbf {s}_{k-1}) - {\mathbb {E}} [D_k] )^+ . \end{aligned}$$

Otherwise, for $n>k$,

$$\begin{aligned}&g_{n,k}((a_1, \ldots , a_{k-1}, a_{k+1}, \ldots , a_n), \mathbf {s}_{n-1})\\&\quad = {\mathbb {E}} [(h_{n-1} ((a_1, \ldots ,a_{k-1}, D_k, a_{k+1}, \ldots , a_{n-1}), \mathbf {s}_{n-1}) - a_{n})^+ ], \\&\qquad {\hat{g}}_{n,k}((a_1, \ldots , a_{k-1}, a_{k+1}, \ldots , a_n), \mathbf {s}_{n-1})\\&\quad = (h_{n-1} ((a_1, \ldots ,a_{k-1}, {\mathbb {E}} [D_k], a_{k+1}, \ldots , a_{n-1}), \mathbf {s}_{n-1}) - a_{n})^+. \end{aligned}$$

By applying Jensen’s inequality and Proposition 4, we may write

$$\begin{aligned} g_{n,k} \ge {\hat{g}}_{n,k}, \end{aligned}$$

(47)

uniformly on ${\mathbb {R}}^{2n-2}$, for $1 \le k \le n \le M$.

Next, we show that for a fixed schedule $\delta = (d_1, d_2, \ldots , d_M)$, the expected waiting time of all customers decreases as we have more punctual customers at the beginning of the schedule. In particular, we want to show

$$\begin{aligned} {\mathbb {E}}[W_n(\Gamma _{k-1})] \ge {\mathbb {E}}[W_n(\Gamma _k)] \quad \text {for } n = 1,2, \ldots , M, \end{aligned}$$

(48)

for every $k = 1,2, \ldots , M$. This means the customer’s expected waiting time under the case where all customers are non-punctual (i.e., ${\mathbb {E}}[W_n(\Gamma _0)]$) is higher than that under the case where all customers are punctual (i.e., ${\mathbb {E}}[W_n(\Gamma _M)]$).

Let $C_0 = d_1$. Therefore, the waiting time and completion time of each customer can be characterized by the following equations:

$$\begin{aligned} W_n&= (C_{n-1} - A_n)^+, \\ C_n&= \max (C_{n-1}, A_n) + S_n \,. \end{aligned}$$

Let $\mathbf {A}_n (\Gamma ) = (A_1 (\Gamma ), A_2 (\Gamma ), \ldots , A_n (\Gamma ))$ and $\mathbf {S}_n = (S_1, S_2, \ldots , S_n)$ denote, respectively, the random vectors of the arrival times and service times of the first n customers with the punctuality profile $\Gamma$. It follows that

$$\begin{aligned} W_n (\Gamma )&= (C_{n-1}(\Gamma ) - A_n (\Gamma ))^+ \quad \text {for } n = 1,\ldots ,M\text {, and} \\ C_n (\Gamma )&= {\left\{ \begin{array}{ll} h_0 = d_1, &{}\quad \quad \text {for } n = 0\\ h_n(\mathbf {A}_n (\Gamma ), \mathbf {S}_n), &{}\quad \quad \text {for } n = 1,\ldots ,M. \end{array}\right. } \end{aligned}$$

Consider a fixed $k = 1, \ldots , M$. The first $k-1$ customers are punctual under both profiles $\Gamma _{k-1}$ and $\Gamma _{k}$. Hence, the expected waiting for customer $n < k$ are the same (i.e., ${\mathbb {E}}[W_n(\Gamma _{k-1})] = {\mathbb {E}}[W_n(\Gamma _k)]$ for $n < k$).

For customer $n = k$, there are two possible cases. If $n=k=1$, we have ${\mathbb {E}}[W_1(\Gamma _{0})] = {\mathbb {E}}[(C_{0}(\Gamma _{0}) - A_1(\Gamma _{0}))^+] = {\mathbb {E}}[(d_1 - D_1)^+]\ge (d_1 - {\mathbb {E}}[D_1])^+= {\mathbb {E}}[(d_1 - {\mathbb {E}}[D_1])^+] = {\mathbb {E}}[(C_{0}(\Gamma _{1}) - A_1(\Gamma _{1}))^+] = {\mathbb {E}}[W_1(\Gamma _{1})]$, where the inequality is obtained by applying Jensen’s inequality. Otherwise, for $n=k>1$, we have

$$\begin{aligned}&{\mathbb {E}}[W_k(\Gamma _{k-1})] \\&\quad = {\mathbb {E}}[(C_{k-1}(\Gamma _{k-1}) - A_k(\Gamma _{k-1}))^+] \\&\quad = {\mathbb {E}}[(h_{k-1} (\mathbf {A}_{k-1} (\Gamma _{k-1}), \mathbf {S}_{k-1}) - D_k)^+] \\&\quad = {\mathbb {E}}[{\mathbb {E}}[(h_{k-1} (\mathbf {A}_{k-1} (\Gamma _{k-1}), \mathbf {S}_{k-1}) - D_k)^+ \mid A_1(\Gamma _{k-1}), \ldots ,\\&\qquad \quad A_{k-1}(\Gamma _{k-1}), \mathbf {S}_{k-1} ]] \\&\quad = {\mathbb {E}}[ g_{k,k} (\mathbf {A}_{k-1}(\Gamma _{k-1}), \mathbf {S}_{k-1}) ] \\&\quad = {\mathbb {E}}[ g_{k,k} (\mathbf {A}_{k-1}(\Gamma _{k}), \mathbf {S}_{k-1}) ] \\&\quad \ge {\mathbb {E}}[ {\hat{g}}_{k,k} (\mathbf {A}_{k-1}(\Gamma _{k}), \mathbf {S}_{k-1}) ] \\&\quad ={\mathbb {E}}[(h_{k-1} ( \mathbf {A}_{k-1} (\Gamma _{k}),\mathbf {S}_{k-1}) - {\mathbb {E}}[D_k])^+] \\&\quad = {\mathbb {E}}[(C_{k-1}(\Gamma _{k}) - A_k(\Gamma _{k}))^+] \\&\quad = {\mathbb {E}}[W_k(\Gamma _{k})]. \end{aligned}$$

The inequality is due to (47) and also the fact that the functions $g_{n,k}$ and ${\hat{g}}_{n,k}$ are integrable given the finite range of customer’s non-punctuality. Similarly, for customer $n>k$, we obtain

$$\begin{aligned}&{\mathbb {E}}[W_n(\Gamma _{k-1})] \\&\quad = {\mathbb {E}}[(C_{n-1}(\Gamma _{k-1}) - A_n(\Gamma _{k-1}))^+] \\&\quad = {\mathbb {E}}[(h_{n-1} (\mathbf {A}_{n-1} (\Gamma _{k-1}), \mathbf {S}_{n-1}) - A_n(\Gamma _{k-1}))^+] \\&\quad = {\mathbb {E}}[{\mathbb {E}}[(h_{n-1} (\mathbf {A}_{n-1} (\Gamma _{k-1}), \mathbf {S}_{n-1}) - A_n(\Gamma _{k-1}))^+ \mid A_1(\Gamma _{k-1}), \ldots ,\\&\qquad \quad A_{k-1}(\Gamma _{k-1}), A_{k+1}(\Gamma _{k-1}), \ldots , A_n(\Gamma _{k-1}), \mathbf {S}_{n-1} ]] \\&\quad = {\mathbb {E}}[ g_{n,k} (A_1(\Gamma _{k-1}), \ldots , A_{k-1}(\Gamma _{k-1}), A_{k+1}(\Gamma _{k-1}), \ldots , A_n(\Gamma _{k-1}), \mathbf {S}_{n-1}) ] \\&\quad = {\mathbb {E}}[ g_{n,k} (A_1(\Gamma _{k}), \ldots , A_{k-1}(\Gamma _{k}), A_{k+1}(\Gamma _{k}), \ldots , A_n(\Gamma _{k}), \mathbf {S}_{n-1}) ] \\&\quad \ge {\mathbb {E}}[ {\hat{g}}_{n,k} (A_1(\Gamma _{k}), \ldots , A_{k-1}(\Gamma _{k}), A_{k+1}(\Gamma _{k}), \ldots , A_n(\Gamma _{k}), \mathbf {S}_{n-1}) ] \\&\quad ={\mathbb {E}}[(h_{n-1} ( A_{1} (\Gamma _{k}), \ldots , A_{k-1} (\Gamma _{k}), {\mathbb {E}}[D_k], A_{k+1} (\Gamma _{k}), \ldots ,\\&\qquad \quad A_{n-1} (\Gamma _{k}), \mathbf {S}_{n-1}) - A_n(\Gamma _{k}))^+ ] \\&\quad ={\mathbb {E}}[(h_{n-1} ( \mathbf {A}_{n-1} (\Gamma _{k}),\mathbf {S}_{n-1}) - A_n(\Gamma _{k}))^+] \\&\quad = {\mathbb {E}}[(C_{n-1}(\Gamma _{k}) - A_n(\Gamma _{k}))^+] \\&\quad = {\mathbb {E}}[W_n(\Gamma _{k})]. \end{aligned}$$

In conclusion, we have proved that (47) holds and that ${\mathbb {E}}[W_n(\Gamma _0)] \ge {\mathbb {E}}[W_n(\Gamma _M)]$, which finishes the proof of the proposition. $\square$

1.2 Proof of Proposition 2

Proof

Consider customer n with the two possible appointment times $\hat{d}_n$ and $d_n$, such that $\hat{d}_n > d_n$. For these two appointment times, the random variables ${\widehat{D}}_n$ and $D_n$ correspond to the arrival times, ${\widehat{V}}_n=C_{n-1}-{\widehat{D}}_n$ and $V_n=C_{n-1}-D_n$ correspond to the difference between the completion time of customer $n-1$ and the arrival time of customer n, and ${\widehat{W}}_n=\max (0,{\widehat{V}}_n)$ and $W_n=\max (0,V_n)$ correspond to the waiting times, respectively. In what follows, we prove that $W_n$ FOS dominates ${\widehat{W}}_n$.

For $t \in [\hat{d}_n-\tau _n^l,\hat{d}_n+\tau _n^u]$, we have $f_{{\widehat{V}}_n}(t)=f_{V_n}(t-(\hat{d}_n-d_n))$. Since $\hat{d}_n - d_n > 0$, ${\widehat{D}}_n$ is stochastically larger than $D_n$. In other words, ${\widehat{D}}_n$ FOS dominates $D_n$. Thus, $-{\widehat{D}}_n$ FOS dominates $-D_n$, which implies, given the independence of $C_{n-1}$, ${\widehat{D}}_n$ and $D_n$, that $C_{n-1}-{\widehat{D}}_n$ FOS dominates $C_{n-1}-D_n$. Since $\max (\cdot ,0)$ is a non-decreasing function, we have that ${\widehat{W}}_n$ FOS dominates $W_n$, which completes the proof of the proposition. $\square$

1.3 Proof of Proposition 3

When arrival times are uniformly distributed, we would like to prove that the expected waiting time of customer n computed using the exact method, ${\mathbb {E}}[W_n]$, is bounded above by the one computed using the approximate method, ${\mathbb {E}}[{{\widetilde{W}}}_n]$. In other words, we want to show that

$$\begin{aligned} {\mathbb {E}}[W_n] ~ \le ~ {\mathbb {E}}[{\widetilde{W}}_n], \quad \text { for} \quad 1\le n \le M, \end{aligned}$$

(49)

with $\displaystyle f_n (x) = \frac{1}{ \tau _n^l +\tau _n^u}$ on $[d_n-\tau _n^l, d_n+\tau _n^u]$ and $f_n (x) =0$ otherwise.

Moreover, we want to prove

$$\begin{aligned} ({\tilde{p}}_{n,i\ge 0}, {\tilde{p}}_{n,i\ge 1}, \ldots , {\tilde{p}}_{n,i\ge n-1}) \prec ^w (p_{n,i\ge 0}, p_{n,i\ge 1}, \ldots , p_{n,i\ge n-1}), \end{aligned}$$

for $1 \le n \le M$, where ${\tilde{p}}_{n,i\ge l} = \sum \nolimits _{i=l}^{n-1} {\tilde{p}}_{n,i}$ and $p_{n,i\ge l} = \sum \nolimits _{i=l}^{n-1} p_{n,i}$.

First, we state several definitions and results that will be used throughout the proof. For any $x=(x_1,\ldots ,x_n) \in {\mathbb {R}}^n$, let $x_{[1]} \ge \cdots \ge x_{[n]}$ denote the components of x in decreasing order, and let $x_{\downarrow } = (x_{[1]}, \ldots , x_{[n]})$ denote the decreasing rearrangement of x. Similarly, let $x_{(1)} \le \cdots \le x_{(n)}$ denote the components of x in increasing order, and let $x_{\uparrow } = (x_{(1)}, \ldots , x_{(n)})$ denote the increasing arrangement of x. Let ${\mathbb {D}}$ denote the subspace of descending vectors in ${\mathbb {R}}^n$, in particular ${\mathbb {D}} = \{(x_1,\ldots ,x_n): x_1\ge \cdots \ge x_n\}$. Similarly, we have $\mathbb {D^+} = \{(x_1,\ldots ,x_n): x_1\ge \cdots \ge x_n \ge 0\}$.

Definition 3

For $x,y \in {\mathbb {R}}^n$,

$$\begin{aligned} x \prec _w y \quad \quad \text {if} \quad \sum _1^k x_{[i]} \le \sum _1^k y_{[i]}, \quad k = 1,\ldots , n, \end{aligned}$$

and

$$\begin{aligned} x \prec ^w y \quad \quad \text {if} \quad \sum _1^k x_{(i)} \ge \sum _1^k y_{(i)}, \quad k = 1,\ldots , n. \end{aligned}$$

x is said to be weakly submajorized by y, if $x \prec _w y$, and x is said to be weakly supermajorized by y, if $x \prec ^w y$. In either case, x is said to be weakly majorized by y (y weakly majorizes x). Moreover, x is said to be majorized by y (y majorizes x), denoted by $x \prec y$ if both cases hold.

It is easy to see that

$$\begin{aligned} x \prec y \Leftrightarrow -x \prec -y,\ \end{aligned}$$

(50)

$$\begin{aligned} x \prec _w y \Leftrightarrow -x \prec ^w -y. \end{aligned}$$

(51)

Theorem 1

(Theorem A.7, p.86 in [26])

Let $\phi$ be a real-valued function, defined and continuous on ${\mathbb {D}}$, and continuously differentiable on the interior of ${\mathbb {D}}$. Denote the partial derivative of $\phi$ with respect to its kth argument by $\phi _{(k)}$: $\phi _{(k)}(z) = \partial \phi (z)/\partial z_k$. Then,

$$\begin{aligned} \phi (x) \le \phi (y) \quad \text {whenever} \quad x \prec _w y \text { on } {\mathbb {D}}, \end{aligned}$$

if and only if,

$$\begin{aligned} \phi _{(1)}(z) \ge \phi _{(2)}(z) \ge \cdots \ge \phi _{(n)}(z) \ge 0, \end{aligned}$$

i.e., the gradient $\nabla \phi (z) \in {\mathbb {D}}$, for all z in the interior of ${\mathbb {D}}$.

Lemma 1

(Theorem H.3.b, p.136 in [26])

If $x,y \in {\mathbb {D}}$ and $x \prec _w y$, then

$$\begin{aligned} \sum {x_i u_i} \le \sum {y_i u_i} \quad \quad \text {for all} \quad u \in {\mathbb {D}}^+. \end{aligned}$$

Proposition 5

If $x,y \in {\mathbb {D}}$ and $y \prec ^w x$, then for each $k \in \{ 1,\ldots , n\}$, we have

$$\begin{aligned} \sum _{i = k}^n{x_i u_{i-k+1}} \le \sum _{i = k}^n{y_i u_{i-k+1}}, \quad \quad \text { for all} \quad u \in {\mathbb {I}}^+, \end{aligned}$$

where $\mathbb {I^+} = \{(x_1,\ldots ,x_n): 0\le x_1\le \cdots \le x_n\}$.

Proof

Take $x,y\in {\mathbb {D}}$ with $y \prec ^w x$. Let ${\hat{x}}$ be the reverse arrangement of x, in particular

$$\begin{aligned} {\hat{x}}_i = x_{n+1-i}, \quad \text { for } i \in \{1,\ldots , n\}, \end{aligned}$$

and by definition we have ${\hat{y}} \prec ^w {\hat{x}}$. Using Eq. (51), we have $-{\hat{y}} \prec _w -{\hat{x}}$ with $-{\hat{x}} \in {\mathbb {D}}$ and $-{\hat{y}} \in {\mathbb {D}}$. Take $u \in \mathbb {I^+}$ and let ${\hat{u}}$ be the reverse arrangement of u. We have ${\hat{u}} \in \mathbb {D^+}$. Moreover, for any $k \in \{1,\ldots ,n\}$, we have

$$\begin{aligned}&(-{\hat{y}}_1, \ldots , -{\hat{y}}_{n-k+1}) \prec _w (-{\hat{x}}_1, \ldots , -{\hat{x}}_{n-k+1}), \\&(-{\hat{y}}_1, \ldots , -{\hat{y}}_{n-k+1})\in {\mathbb {D}}, \quad (-{\hat{x}}_1, \ldots , -{\hat{x}}_{n-k+1}) \in {\mathbb {D}}, \\&({\hat{u}}_k, \ldots , {\hat{u}}_n) \in \mathbb {D^+}. \end{aligned}$$

It follows from Lemma 1 that

$$\begin{aligned} \sum _{i=1}^{n-k+1}{-{\hat{y}}_i {\hat{u}}_{i+k-1}} \le \sum _{i=1}^{n-k+1}{-{\hat{x}}_i {\hat{u}}_{i+k-1}}, \end{aligned}$$

and therefore we obtain

$$\begin{aligned} \sum _{i=k}^{n}{x_{i} u_{i-k+1}} =&\, \sum _{i=k}^{n}{{\hat{x}}_{n+1-i} {\hat{u}}_{n+k-i}} \\ =&\, \sum _{i=1}^{n-k+1}{{\hat{x}}_i {\hat{u}}_{i+k-1}} \\ \le&\sum _{i=1}^{n-k+1}{{\hat{y}}_i {\hat{u}}_{i+k-1}} \\ =&\, \sum _{i=k}^{n}{{\hat{y}}_{n+1-i} {\hat{u}}_{n+k-i}} = \sum _{i=k}^{n}{y_{i} u_{i-k+1}}. \end{aligned}$$

Note that this proposition could be also proven by applying Theorem 1 with $\phi (z) = \sum \nolimits _{i=1}^k -z_{n+1-i} u_{k+1-i}$, for $k \in \{1,\ldots ,n\}$. $\square$

Theorem 2

(Chebyshev Integral Inequality) (Theorem 9, p.39 in [31])

Let f and g be real and integrable functions on [a, b] and let them both be either increasing or decreasing. Then,

$$\begin{aligned} \frac{1}{b-a} \int _a^b f(x) g(x) \mathrm{d}x \ge \frac{1}{b-a} \int _a^b f(x) dx \, \frac{1}{b-a} \int _a^b g(x) \mathrm{d}x. \end{aligned}$$

If one function is increasing and the other is decreasing, the reverse inequality holds.

We use the tilde sign to denote variables computed using the approximation method, such as ${\widetilde{W}}_n$ for the customer’s waiting time. Let us define the following notation:

$$\begin{aligned} p_{n,i\ge l} = \sum _{i=l}^{n-1} p_{n,i}, \end{aligned}$$

and

$$\begin{aligned} p_{n,i\le l} = \sum _{i=0}^{l} p_{n,i}, \end{aligned}$$

for $0\le l \le n-1$, and similarly for $\tilde{p}_{n,i\ge l}$ and $\tilde{p}_{n,i\le l}$. We use $g (n, \lambda )$ and $G (n, \lambda )$ to denote the pdf and cdf of a Poisson distribution with rate $\lambda$. We have $g(n, \lambda ) = \frac{ \lambda ^{n}}{n!} e^{-\lambda }$ and $G(n, \lambda ) = \sum _{i=0}^n\frac{ \lambda ^{i}}{i!} e^{-\lambda }$ if $n\ge 0$, and $g(n, \lambda )=G(n, \lambda )=0$ otherwise.

Let us recall the differences between the exact and approximate methods we developed in the main paper. Instead of the conditional distribution of inter-arrival time $h_{n,j}(\cdot )$ used in the exact method (as shown in Eq. (9)), we use the unconditional inter-arrival time distribution $h_{n}(\cdot )$ as the approximation for $3 \le n \le M$ (as shown in Eq. (35)). Since no approximation is involved in the computation of ${\tilde{p}}_{n,i}$ for $n = 1,2$, the expected waiting time for customers 1 and 2 are the same from both methods. Therefore, to prove Eq. (49), we only need to show

$$\begin{aligned} {\mathbb {E}}[W_n] ~ \le ~ {\mathbb {E}}[{\widetilde{W}}_n] \quad \text {, for} \quad 3 \le n \le M, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \sum _{l=1}^{n-1} p_{n,i\ge l} ~ \le ~ \sum _{l=1}^{n-1} {\tilde{p}}_{n,i\ge l}, \end{aligned}$$

(52)

for $3 \le n \le M$.

In the following, we use induction to prove that

$$\begin{aligned} ({\tilde{p}}_{n,i\ge 0}, {\tilde{p}}_{n,i\ge 1}, \ldots , {\tilde{p}}_{n,i\ge n-1}) \prec ^w (p_{n,i\ge 0}, p_{n,i\ge 1}, \ldots , p_{n,i\ge n-1}), \end{aligned}$$

(53)

for $3 \le n \le M$. By definition, Eq. (53) leads to

$$\begin{aligned} \sum _{l=0}^{n-1} p_{n,i\ge l} ~ \le ~ \sum _{l=0}^{n-1} {\tilde{p}}_{n,i\ge l}, \end{aligned}$$

(54)

which is equivalent to Eq. (52), since $p_{n,i\ge 0} = {\tilde{p}}_{n,i\ge 0} = 1$.

Initialization: For $n=2$, we have $p_{2,i\ge l} = {\tilde{p}}_{2,i\ge l}$ for $l=0,1$, as no approximation is involved when computing ${\tilde{p}}_{n,i}$. By definition, we have

$$\begin{aligned} ({\tilde{p}}_{2,i\ge 0}, {\tilde{p}}_{2,i\ge 1}) \prec ^w (p_{2,i\ge 0}, p_{2,i\ge 1}). \end{aligned}$$

Induction: Assume Eq. (53) holds for $n-1$, which gives

$$\begin{aligned} ({\tilde{p}}_{n-1,i\ge 0}, {\tilde{p}}_{n-1,i\ge 1}, \ldots , {\tilde{p}}_{n-1,i\ge n-2}) \prec ^w (p_{n-1,i\ge 0}, p_{n-1,i\ge 1}, \ldots , p_{n-1,i\ge n-2}). \end{aligned}$$

(55)

Let us prove that

$$\begin{aligned} \sum _{l=k}^{n-1} p_{n,i\ge l} ~ \le ~ \sum _{l=k}^{n-1} {\tilde{p}}_{n,i\ge l} \quad \text {for} \quad 0 \le k \le n-1. \end{aligned}$$

(56)

This reduces to proving that

$$\begin{aligned} \sum _{l=k}^{n-1} p_{n,i\ge l} ~ \le ~ \sum _{l=k}^{n-1} {\tilde{p}}_{n,i\ge l} \quad \text {for} \quad 1 \le k \le n-1, \end{aligned}$$

(57)

since $p_{n,i\ge 0} = {\tilde{p}}_{n,i\ge 0} = 0$.

We start by providing an equivalent formation of $\text{ Pr }\{R_n =i \mid R_{n-1}=j\}$ as compared to that used in Eqs. (8) and (9). Instead of conditioning on the inter-arrival time between customers $n-1$ and n, we can compute $\text{ Pr }\{R_n =i \mid R_{n-1}=j\}$ by conditioning on the arrival time of customer $n-1$, where we have

$$\begin{aligned}&\text{ Pr }\{R_n =i \mid R_{n-1}=j\} \nonumber \\&\quad = \int _{d_{n}-\tau _{n}^l}^{d_{n}+\tau _{n}^u} \int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u} \text{ Pr }\{R_n =i \mid R_{n-1}=j, D_{n-1}=v, D_{n}=u\} \nonumber \\&\qquad f_{n-1,j}(v) f_n(u) \,\mathrm{d}v \,\mathrm{d}u \nonumber \\&\quad = \int _{d_{n}-\tau _{n}^l}^{d_{n}\!+\!\tau _{n}^u} \int _{d_{n-1}\!-\!\tau _{n-1}^l}^{d_{n-1}\!+\!\tau _{n-1}^u} [\alpha _{n-1} g(j+1-i, (u-v)\mu )\!+\! (1\!-\!\alpha _{n-1}) g(j-i, (u\!-\!v)\mu ) ]\nonumber \\&\qquad f_{n-1,j}(v) f_n(u) \,\mathrm{d}v \,\mathrm{d}u, \end{aligned}$$

(58)

for $0 \le j \le n-2$ and $0 \le i \le j+1$.

Thus,

$$\begin{aligned} \sum _{l=k}^{n-1} p_{n,i\ge l} =&\,\sum _{l=k}^{n-1} \sum _{i=l}^{n-1} p_{n,i} \nonumber \\ =&\,\sum _{l=k}^{n-1} \sum _{i=l}^{n-1} \sum _{j=i-1}^{n-2} p_{n-1,j} \text{ Pr }\{R_n =i \mid R_{n-1}=j\} \nonumber \\ =&\,\sum _{l=k}^{n-1} \sum _{i=l}^{n-1} \sum _{j=i-1}^{n-2} p_{n-1,j} \int _{d_{n}-\tau _{n}^l}^{d_{n}+\tau _{n}^u} \int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u} \big [\alpha _{n-1} g(j+1-i, (u-v)\mu ) \nonumber \\&+ (1-\alpha _{n-1}) g(j-i, (u-v)\mu ) \big ] f_{n-1,j}(v) f_n(u) \,\mathrm{d}v \,\mathrm{d}u \nonumber \\ =&\, \int _{d_{n}-\tau _{n}^l}^{d_{n}+\tau _{n}^u} f_n(u) \int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u} \sum _{l=k}^{n-1} \sum _{i=l}^{n-1} \sum _{j=i-1}^{n-2} \big [\alpha _{n-1} g(j+1-i, (u-v)\mu ) \nonumber \\&+ (1-\alpha _{n-1}) g(j-i, (u-v)\mu ) \big ] p_{n-1,j} f_{n-1,j}(v) \,\mathrm{d}v \,\mathrm{d}u \nonumber \\ =&\, \int _{d_{n}-\tau _{n}^l}^{d_{n}+\tau _{n}^u} f_n(u) \int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u} f_{n-1}(v) \sum _{l=k}^{n-1} \sum _{i=l}^{n-1} \sum _{j=i-1}^{n-2} \nonumber \\&\big [\alpha _{n-1} g(j+1-i, (u-v)\mu ) \nonumber \\&+ (1-\alpha _{n-1}) g(j-i, (u-v)\mu ) \big ] p_{n-1,j \mid D_{n-1}=v} \,\mathrm{d}v \,\mathrm{d}u \nonumber \\ =&\, \int _{d_{n}-\tau _{n}^l}^{d_{n}+\tau _{n}^u} f_n(u) \int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u} f_{n-1}(v) \Big [\alpha _{n-1} \sum _{l=k-1}^{n-2} \nonumber \\&G(l-k+1, (u-v)\mu ) p_{n-1,i \ge l \mid D_{n-1}=v} \nonumber \\&+ (1-\alpha _{n-1}) \sum _{l=k}^{n-2} G(l-k, (u-v)\mu ) p_{n-1,i \ge l \mid D_{n-1}=v} \Big ]\,\mathrm{d}v \,\mathrm{d}u \nonumber \\&\begin{aligned} =&\, \int _{d_{n}-\tau _{n}^l}^{d_{n}+\tau _{n}^u} f_n(u) \Big [\alpha _{n-1} \sum _{l=k-1}^{n-2} \int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u} f_{n-1}(v) \\&G(l-k+1, (u-v)\mu ) p_{n-1,i \ge l \mid D_{n-1}=v} \,\mathrm{d}v \\&+ (1-\alpha _{n-1}) \sum _{l=k}^{n-2} \int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u} f_{n-1}(v)\\&G(l-k, (u-v)\mu ) p_{n-1,i \ge l \mid D_{n-1}=v} \,\mathrm{d}v \Big ] \,\mathrm{d}u. \end{aligned} \end{aligned}$$

(59)

Since $f_{n-1}(v)$ is constant on $[d_{n-1}-\tau _{n-1}^l, d_{n-1}+\tau _{n-1}^u]$, together with Theorem 2, we obtain

$$\begin{aligned} \begin{aligned}&\int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u} f_{n-1}(v) G(l-k+1, (u-v)\mu ) p_{n-1,i \ge l \mid D_{n-1}=v} \,\mathrm{d}v \\&\quad \le \int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u} f_{n-1}(v) G(l-k+1, (u-v)\mu ) \,\mathrm{d}v \int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u}\\&\qquad f_{n-1}(v) p_{n-1,i \ge l \mid D_{n-1}=v} \,\mathrm{d}v \\&\quad = {\mathbb {E}}_{{D_{n-1}}}\big [ G(l-k+1, (u- D_{n-1})\mu ) \big ] \int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u} f_{n-1,i \ge l}(v) p_{n-1,i \ge l } \,\mathrm{d}v \\&\quad = {\mathbb {E}}_{{D_{n-1}}}\big [ G(l-k+1, (u- D_{n-1})\mu ) \big ] p_{n-1,i \ge l } \int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u} f_{n-1,i \ge l}(v) \,\mathrm{d}v \\&\quad = {\mathbb {E}}_{{D_{n-1}}}\big [ G(l-k+1, (u- D_{n-1})\mu ) \big ] p_{n-1,i \ge l }, \end{aligned} \end{aligned}$$

(60)

where $f_{n-1,i \ge l}(v)$ is the pdf of the conditional arrival time of customer $n-1$, given she finds equal or more than l customers in system upon her arrival. The first equality in Eq. (60) is derived by applying Bayes’ theorem. In particular,

$$\begin{aligned} f_{n-1,i\ge l}(t)=\frac{p_{n-1,i\ge l|D_{n-1}=t}\times f_{n-1}(t)}{p_{n-1,i\ge l}} \,. \end{aligned}$$

Similarly, we can write

$$\begin{aligned} \begin{aligned}&\int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u} f_{n-1}(v) G(l-k, (u-v)\mu ) p_{n-1,i \ge l \mid D_{n-1}=v} \,\mathrm{d}v \\ \le&{\mathbb {E}}_{{D_{n-1}}}\big [ G(l-k, (u- D_{n-1})\mu ) \big ] p_{n-1,i \ge l }. \end{aligned} \end{aligned}$$

(61)

Substituting Eq. (59) with Eqs. (60) and (61) gives

$$\begin{aligned}&\sum _{l=k}^{n-1} p_{n,i\ge l} \nonumber \\&\begin{aligned} \le&\int _{d_{n}-\tau _{n}^l}^{d_{n}+\tau _{n}^u} f_n(u) \Big [\alpha _{n-1} \sum _{l=k-1}^{n-2} {\mathbb {E}}_{{D_{n-1}}}\big [ G(l-k+1, (u- D_{n-1})\mu )\big ] p_{n-1,i \ge l } \\& + (1-\alpha _{n-1}) \sum _{l=k}^{n-2} {\mathbb {E}}_{{D_{n-1}}}\big [ G(l-k, (u- D_{n-1})\mu ) \big ] p_{n-1,i \ge l } \Big ] \,\mathrm{d}u. \end{aligned} \end{aligned}$$

(62)

Next, we compute $\sum _{l=k}^{n-1} {\tilde{p}}_{n,i\ge l}$ with a characterization of ${\tilde{p}}_{n,i}$ that is equivalent to what we used in our approximation. In the approximation method, we approximate $h_{n-1,j}$ in Eq. (9) by $h_{n-1}$, which leads to

$$\begin{aligned} {\tilde{p}}_{n,i} =&\, \alpha _{n-1} \sum _{j=i-1}^{n-2} {\tilde{p}}_{n-1,j} \int _{d_n-d_{n-1}-\tau _n^l-\tau _{n-1}^u}^{d_n-d_{n-1}+\tau _n^u+\tau _{n-1}^l} g(j+1-i, x\mu ) h_{n-1}(x) \,\mathrm{d}x \nonumber \\&+(1-\alpha _{n-1}) \sum _{j=i}^{n-2} {\tilde{p}}_{n-1,j} \int _{d_n-d_{n-1}-\tau _n^l-\tau _{n-1}^u}^{d_n-d_{n-1}+\tau _n^u+\tau _{n-1}^l} g(j-i, x\mu ) h_{n-1}(x) \,\mathrm{d}x, \end{aligned}$$

(63)

with

$$\begin{aligned} h_{n-1}(x) =&\, \int _{\max {(d_n-\tau _n^l, d_{n-1}-\tau _{n-1}^l+x)}}^{\min {(d_n+\tau _n^u, d_{n-1}+\tau _{n-1}^u+x)}} f_{n}(u) f_{n-1}(u-x) \,\mathrm{d}u \nonumber \\&\text {for } x \in [d_n-d_{n-1}+\tau _n^u+\tau _{n-1}^l,d_n-d_{n-1}-\tau _n^l-\tau _{n-1}^u] . \end{aligned}$$

(64)

We can substitute $h_{n-1}(x)$ and reformulate ${\tilde{p}}_{n,i}$ by changing the integration variables and ranges, which gives

$$\begin{aligned} \begin{aligned} {\tilde{p}}_{n,i} =&\, \sum _{j=i-1}^{n-2} {\tilde{p}}_{n-1,j} \int _{d_{n}-\tau _{n}^l}^{d_{n}+\tau _{n}^u} f_n(u) \int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u} f_{n-1}(v) \big [\alpha _{n-1} g(j+1-i, (u-v)\mu ) \\&+ (1-\alpha _{n-1}) g(j-i, (u-v)\mu ) \big ] \,\mathrm{d}v \,\mathrm{d}u. \end{aligned} \end{aligned}$$

(65)

Then, we can compute $\sum \nolimits _{l=k}^{n-1} {\tilde{p}}_{n,i\ge l}$ by using Eq. (65). This implies

$$\begin{aligned}&\sum _{l=k}^{n-1} {\tilde{p}}_{n,i\ge l} \nonumber \\&\quad =\sum _{l=k}^{n-1} \sum _{i=l}^{n-1} \sum _{j=i-1}^{n-2} {\tilde{p}}_{n-1,j} \int _{d_{n}-\tau _{n}^l}^{d_{n}+\tau _{n}^u} \int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u} \big [\alpha _{n-1} g(j+1-i, (u-v)\mu ) \nonumber \\&\qquad + (1-\alpha _{n-1}) g(j-i, (u-v)\mu ) \big ] f_{n-1}(v) f_n(u) \,\mathrm{d}v \,\mathrm{d}u \nonumber \\&\quad = \int _{d_{n}-\tau _{n}^l}^{d_{n}+\tau _{n}^u} f_n(u) \int _{d_{n-1}-\tau _{n-1}^l}^{d_{n-1}+\tau _{n-1}^u} f_{n-1}(v) \Big [\alpha _{n-1} \sum _{l=k-1}^{n-2} G(l-k+1, (u-v)\mu ) {\tilde{p}}_{n-1,i\ge l} \,\mathrm{d}v \nonumber \\&\qquad + (1-\alpha _{n-1}) \sum _{l=k}^{n-2} G(l-k, (u-v)\mu ) {\tilde{p}}_{n-1,i\ge l} \Big ]\,\mathrm{d}v \,\mathrm{d}u \nonumber \\&\begin{aligned} =&\, \int _{d_{n}-\tau _{n}^l}^{d_{n}+\tau _{n}^u} f_n(u) \Big [\alpha _{n-1} \sum _{l=k-1}^{n-2} {\mathbb {E}}_{{D_{n-1}}}\big [ G(l-k+1, (u- D_{n-1})\mu ) \big ] {\tilde{p}}_{n-1,i \ge l } \\&+ (1-\alpha _{n-1}) \sum _{l=k}^{n-2} {\mathbb {E}}_{{D_{n-1}}}\big [ G(l-k, (u- D_{n-1})\mu ) \big ] {\tilde{p}}_{n-1,i \ge l } \Big ] \,\mathrm{d}u. \end{aligned} \end{aligned}$$

(66)

Finally, we are ready to show that Eq. (57) holds. By assumption, it follows from Eq. (55) that

$$\begin{aligned} ({\tilde{p}}_{n-1,i\ge k}, {\tilde{p}}_{n-1,i\ge k+1}, \ldots , {\tilde{p}}_{n-1,i\ge n-2}) \prec ^w (p_{n-1,i\ge k}, p_{n-1,i\ge k+1}, \ldots , p_{n-1,i\ge n-2}), \end{aligned}$$

for all $k = 1, \ldots , n-2$. For fixed $u \in [ d_{n}-\tau _{n}^l, d_{n}+\tau _{n}^u]$, it is obvious that $\Big ( {\mathbb {E}}_{{D_{n-1}}}\big [ G(l, (u- D_{n-1})\mu \big ] \Big )_{l=1}^{n-2}$ and $\Big ( {\mathbb {E}}_{{D_{n-1}}}\big [ G(l-1, (u- D_{n-1})\mu \big ] \Big )_{l=1}^{n-2}$ are positive and increasing in l. Therefore, according to Proposition 5, we have

$$\begin{aligned}&\sum _{l=k}^{n-2} {\mathbb {E}}_{{D_{n-1}}}\big [ G(l-k+1, (u- D_{n-1})\mu ) \big ] p_{n-1,i \ge l }\\&\qquad \le \sum _{l=k}^{n-2} {\mathbb {E}}_{{D_{n-1}}} \big [ G(l-k+1, (u- D_{n-1})\mu ) \big ] {\tilde{p}}_{n-1,i \ge l }, \end{aligned}$$

which leads to

$$\begin{aligned}&\sum _{l=k-1}^{n-2} {\mathbb {E}}_{{D_{n-1}}}\big [ G(l-k+1, (u- D_{n-1})\mu ) \big ] p_{n-1,i \ge l } \nonumber \\&\quad \le \sum _{l=k-1}^{n-2} {\mathbb {E}}_{{D_{n-1}}}\big [ G(l-k+1, (u- D_{n-1})\mu ) \big ] {\tilde{p}}_{n-1,i \ge l }, \end{aligned}$$

(67)

since $p_{n-1,i \ge 0 } = {\tilde{p}}_{n-1,i \ge 0 } = 1$. Also, according to Proposition 5, we have

$$\begin{aligned}&\sum _{l=k}^{n-2} {\mathbb {E}}_{{D_{n-1}}}\big [ G(l-k, (u- D_{n-1})\mu ) \big ] p_{n-1,i \ge l }\nonumber \\&\quad \le \sum _{l=k}^{n-2} {\mathbb {E}}_{{D_{n-1}}}\big [ G(l-k, (u- D_{n-1})\mu ) \big ] {\tilde{p}}_{n-1,i \ge l } . \end{aligned}$$

(68)

Since Eqs. (67) and (68) hold for all $u \in [ d_{n}-\tau _{n}^l, d_{n}+\tau _{n}^u]$, together with Eqs. (62) and (66), we deduce that

$$\begin{aligned} \sum _{l=k}^{n-1} p_{n,i\ge l} ~ \le ~ \sum _{l=k}^{n-1} {\tilde{p}}_{n,i\ge l} \quad \text {for} \quad 1 \le k \le n-1, \end{aligned}$$

which completes the proof of the proposition. $\square$

Appendix D: Experiments related to Sect. 6

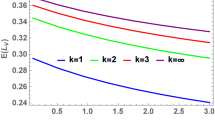
See Fig. 5 and Tables 5, 6, 7, and 8.

Fig. 5

Exact versus approximation ($\tau _n^l=\tau _n^u=\tau =10$, $\alpha _n=\alpha =1$, $x_n=x=20$, $\mu =0.1$)

⁶

Table 5 Comparison between exact and approximate methods: Experiments 1, $\mu = 0.05$

Table 6 Comparison between exact and approximate methods: Experiments 2, $\mu = 0.05$

Table 7 Comparison between exact and approximate methods: Experiments 3, $\mu = 0.05$

Table 8 Comparison between exact and approximate methods: Experiments 4, $\mu = 0.05$