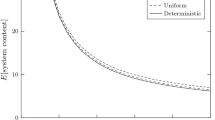
Abstract
We consider an extension of the standard G/G/1 queue, described by the equation \(W\stackrel{ \mathcal {D}}{=}\max\mathrm{max}\,\{0,B-A+YW\}\) , where ℙ[Y=1]=p and ℙ[Y=−1]=1−p. For p=1 this model reduces to the classical Lindley equation for the waiting time in the G/G/1 queue, whereas for p=0 it describes the waiting time of the server in an alternating service model. For all other values of p, this model describes a FCFS queue in which the service times and interarrival times depend linearly and randomly on the waiting times. We derive the distribution of W when A is generally distributed and B follows a phase-type distribution, and when A is exponentially distributed and B deterministic.
References
Asmussen S, Schock Petersen S. Ruin probabilities expressed in terms of storage processes. Adv Appl Probab 1989;20(4):913–6.
Asmussen S, Sigman K. Monotone stochastic recursions and their duals. Probab Eng Inf Sci 1996;10(1):1–20.
Borovkov AA, Foss S. Stochastically recursive sequences. Sib Adv Math 1992;2:16–81.
Brandt A. The stochastic equation Y n+1=A n Y n +B n with stationary coefficients. Adv Appl Probab 1986;18(1):211–20.
Brandt A, Franken P, Lisek B. Stationary stochastic models. vol. 78, Mathematische Lehrbücher und Monographien, II. Abteilung: Mathematische Monographien. Berlin: Akademie Verlag; 1990.
Cohen JW. The single server queue. Amsterdam: North-Holland; 1982.
Erlang AK. The theory of probabilities and telephone conversations. In: Brockmeyer E, Halstrøm HL, Jensen A, editors. The life and works of A.K. Erlang. Applied mathematics and computing machinery series. vol 6. Acta polytechnica Scandinavica. 2nd ed. 1960, p. 131–137. English translation. First published in “Nyt tidsskrift for matematik” B. vol 20. 1909, p. 33.
Franx GJ. A simple solution for the M/D/c waiting time distribution. Oper Res Lett 2001;29(5):221–9.
Jacquet P. Subexponential tail distribution in LaPalice queues. Perform Eval Rev 1992;20(1):60–9.
Kalashnikov V, Norberg R. Power tailed ruin probabilities in the presence of risky investments. Stoch Process Appl 2002;98:211–28.
Lindley DV. The theory of queues with a single server. Proc Camb Philos Soc 1952;48:277–89.
Norberg R. Ruin problems with assets and liabilities of diffusion type. Stoch Process Appl 1999;81:255–69.
Park BC, Park JY, Foley RD. Carousel system performance. J Appl Probab 2003;40(3):602–12.
Ross SM. Stochastic processes. 2nd ed. New York: Wiley; 1996.
Schassberger R. Warteschlangen. Wien: Springer; 1973.
Seal HL. Risk theory and the single server queue. Mitt Ver Schweiz Versicher 1972;72:171–8.
Tang Q, Tsitsiashvili G. Precise estimates for the ruin probability in finite horizon in a discrete-time model with heavy-tailed insurance and financial risks. Stoch Process Appl 2003;108:299–325.
Titchmarsh EC. Theory of functions. 2nd ed. London: Oxford University Press; 1968.
Vervaat W. On a stochastic difference equation and a representation of non-negative infinitely divisible random variables. Adv Appl Probab 1979;11(4):750–83.
Vlasiou M. A non-increasing Lindley-type equation. Technical Report 2005-015, Eurandom, Eindhoven, The Netherlands, 2005. Available at http://www.eurandom.nl.
Vlasiou M, Adan IJBF. An alternating service problem. Probab Eng Inf Sci 2005;19(4):409–26.
Vlasiou M, Adan IJBF. Exact solution to a Lindley-type equation on a bounded support. Oper Res Lett 2007;35(1):105–13.
Vlasiou M, Adan IJBF, Wessels J. A Lindley-type equation arising from a carousel problem. J Appl Probab 2004;41(4):1171–81.
Whitt W. Queues with service times and interarrival times depending linearly and randomly upon waiting times. Queueing Systs 1990;6(4):335–51.
Author information
Authors and Affiliations
Corresponding author
Additional information
This research has been carried out when M. Vlasiou was affiliated with EURANDOM, The Netherlands.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License ( https://creativecommons.org/licenses/by-nc/2.0 ), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Boxma, O.J., Vlasiou, M. On queues with service and interarrival times depending on waiting times. Queueing Syst 56, 121–132 (2007). https://doi.org/10.1007/s11134-007-9011-3
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11134-007-9011-3
Keywords
- Lindley recursion
- G/G/1 queue
- Alternating service model
Mathematics Subject Classification (2000)
- 60K25
- 90B22