Evaluating wireless carrier consolidation using semiparametric demand estimation

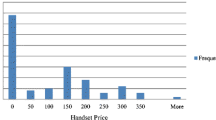
Abstract

The US mobile phone service industry has dramatically consolidated over the last two decades. One justification for consolidation is that merged firms can provide consumers with larger coverage areas at lower costs. We estimate the willingness to pay for national coverage to evaluate this justification for past consolidation. As market level quantity data are not publicly available, we devise an econometric procedure that allows us to estimate the willingness to pay using market share ranks collected from the popular online retailer Amazon. Our semiparametric maximum score estimator controls for consumers’ heterogeneous preferences for carriers, handsets and minutes of calling time. We find that national coverage is strongly valued by consumers, providing an efficiency justification for across-market mergers. The methods we propose can estimate demand for other products using data from online retailers where product ranks, but not quantities, are observed.

A Proofs

1.1 A.1 Lemma 1

In what follows, drop the indices i and m, and use the shorthand notation a _j for $x_{jm}^{'}\beta-p_{jm}+\nu_{im}^{h}$. Also replace the conditioning arguments J _m ,H _m ,X _m , $\vec{p}_{m},I_{m},\left\{ \vec{\nu}_{im}\right\} _{i\in I_{m,}}$ of the densities of ε _j and ξ _j with $\vec{a}$, the vector of the J a _j ’s.

Both ε _j and ξ _j are not in the data. The joint density of all J ε _J ’s and ξ _j ’s is

$$ c\left(\vec{\varepsilon},\vec{\xi}\mid\vec{a}\right)=\prod\limits_{h\in H}\prod\limits_{k\in H}f_{h}\left(\varepsilon_{j}\mid\vec{a},\vec{\xi}\right)\cdot\prod\limits_{h\in H}\prod\limits_{k\in H}g_{h}\left(\xi_{k}\mid\vec{a}\right).$$

First we will integrate out ε. Let $\mbox{Pr}\left(j\mid\vec{a},\vec{\xi}\right)$ be the probability of picking j conditional on the realization of the ξ _j ’s. The decision rule in Eq. (3) becomes

$$ \varepsilon_{l}<a_{j}-a_{l}+\varepsilon_{j}+\xi_{j}-\xi_{l}$$

for all choices l.

First prove the “only if” direction: If a _j  + ξ _j  > a _k  + ξ _k , then $\mbox{Pr}\left(j\mid\vec{a},\vec{\xi}\right)>\mbox{Pr}\left(k\mid\vec{a},\vec{\xi}\right)$. By the definition of a choice probability,

$$ \begin{array}{lll} \mbox{Pr}\left(j\mid\vec{a},\vec{\xi}\right)&=&\int_{-\infty}^{\infty}\left(\vphantom{\cdot\left.\prod\limits_{l=1,l\neq j,k}^{J}\left\{ \int_{-\infty}^{a_{j}-a_{l}+\varepsilon_{j}+\xi_{j}-\xi_{l}}f_{h\left(l\right)}\left(\varepsilon_{l}\mid\vec{a},\vec{\xi}\right)d\varepsilon_{l}\!\right\} \!\right)\!\cdot\! f_{h\left(j\right)}\left(\varepsilon_{j}\mid\vec{a},\vec{\xi}\right)d\varepsilon_{j},} \left\{ \int_{-\infty}^{a_{j}-a_{k}+\varepsilon_{j}+\xi_{j}-\xi_{k}}f_{h\left(k\right)}\left(\varepsilon_{k}\mid\vec{a},\vec{\xi}\right)d\varepsilon_{k}\right\} \right.\\\\ &&{\kern32pt} \cdot\left.\prod_{l=1,l\neq j,k}^{J}\left\{ \int_{-\infty}^{a_{j}-a_{l}+\varepsilon_{j}+\xi_{j}-\xi_{l}}f_{h\left(l\right)}\left(\varepsilon_{l}\mid\vec{a},\vec{\xi}\right)d\varepsilon_{l}\!\right\} \!\right)\\\\ &&{\kern32pt} \cdot f_{h\left(j\right)}\left(\varepsilon_{j}\mid\vec{a},\vec{\xi}\right)d\varepsilon_{j}, \end{array} $$

where $h\left(l\right)$ is a convenience function returning the nest of choice l. If $h\left(j\,\right)=$ $h\left(k\right)$, as in the statement of the lemma, $\mbox{Pr}\left(j\mid\vec{a},\vec{\xi}\right)$ is the same function as $\mbox{Pr}\left(k\mid\vec{a},\vec{\xi}\right)$, except that a _k  + ξ _k replaces a _j  + ξ _j in the upper limits, and a _j  + ξ _j replaces the one term where a _k  + ξ _k enters in $\mbox{Pr}\left(j\mid\vec{a},\vec{\xi}\right)$. Let $W\left(a_{j}+\xi_{j},a_{k}+\xi_{k}\right)$ be $\mbox{Pr}\left(j\mid\vec{a},\vec{\xi}\right)$ as a function of a _j  + ξ _j and a _k  + ξ _k .

As a _j  + ξ _j enters only upper limits of integrals in $W\left(a_{j}+\xi_{j},a_{k}+\xi_{k}\right)$ , $W\left(a_{j}+\xi_{j},a_{k}+\xi_{k}\right)$ is increasing in a _j  + ξ _j . Also, a _k  + ξ _k enters negatively in only one upper limit in $W\left(a_{j}+\xi_{j},a_{k}+\xi_{k}\right)$. Because $f_{h\left(j\right)}\left(\varepsilon_{j}\mid\vec{a},\vec{\xi}\right)$ has full support by Assumption 1, $W\left(a_{j}+\xi_{j},a_{k}+\xi_{k}\right)$ is strictly increasing in a _j  + ξ _k and strictly decreasing in a _k  + ξ _k . Then if a _j  + ξ _k  > a _k  + ξ _k , as in the statement of the lemma, $W\left(a_{j}+\xi_{j},a_{k}+\xi_{k}\right)>W\left(a_{k}+\xi_{k},a_{j}+\xi_{j}\right)$. Likewise, the “if” direction is proved as the only way $W\left(a_{j}+\xi_{j},a_{k}+\xi_{k}\right)>W\left(a_{k}+\xi_{k},a_{j}+\xi_{j}\right)$ is if a _j  + ξ _j  > a _k  + ξ _k .

The above argument conditioned on $\vec{\xi}$. We need to prove statements about $\mbox{Pr}\left(j\mid\vec{a}\right)$ and $\mbox{Pr}\left(k\mid\vec{a}\right)$. Again by the definition of a choice probability,

$$ \mbox{Pr}\left(j\mid\vec{a},\vec{\xi}\right)=\int_{-\infty}^{\infty}\mbox{Pr}\left(j\mid\vec{a},\vec{\xi}\right)\prod\limits_{h\in H}\prod\limits_{k\in H}g_{h}\left(\xi_{k}\mid\vec{a}\right)d\vec{\xi}.$$

Because Assumption 1 states each $f_{h\left(j\right)}\left(\varepsilon_{j}\mid\vec{a},\vec{\xi}\right)$ is exchangeable in the arguments ξ _j and ξ _k when $h\left(j\right)=h\left(k\right)$ and the ξ _jm ’s are i.i.d. within a nest, then $\mbox{Pr}\left(j\mid\vec{a}\right)$ is the same function as $\mbox{Pr}\left(k\mid\vec{a}\right)$, except where a _j and a _k enter the upper limits in $\mbox{Pr}\left(j\mid\vec{a},\vec{\xi}\right)$. By a similar argument as with the W function above, the lemma is proved.

1.2 A.2 Lemma 2

Because expectation and integration are linear operators, conditioning on the number of consumers I _m results in:

$$ \begin{array}{lll} &&{\kern-8.5pt} E\left[s_{jm}\mid I_{m},J_{m},H_{m},X_{m},\vec{p}_{m}\right]\\ &&{\kern2pt} =E\left[\frac{1}{I_{m}}\sum\limits_{i=1}^{I_{m}}1\left[i\,\mathrm{buys}\, j\right]\mid I_{m},J_{m},H_{m},X_{m},\vec{p}_{m}\right]\\ &&{\kern2pt}=\frac{1}{I_{m}}\sum\limits_{i=1}^{I_{m}}E\left[1\left[i\,\mathrm{buys}\, j\right]\mid I_{m},J_{m},H_{m},X_{m},\vec{p}_{m}\right]\\ &&{\kern2pt}=\frac{1}{I_{m}}\sum\limits_{i=1}^{I_{m}}E\left[E_{\varepsilon,\xi}\left[1\left[i\,\mathrm{buys}\, j\right]\mid\left\{ \vec{\nu}_{im}\right\} _{i\in I_{m,}},I_{m},J_{m},H_{m},X_{m},\vec{p}_{m}\right]\right.\\ &&{\kern57pt} \left. \mid I_{m},J_{m},H_{m},X_{m},\vec{p}_{m}\right]\\ &&{\kern2pt}=\frac{1}{I_{m}}\sum\limits_{i=1}^{I_{m}}E\left[\mbox{Pr}_{im}\left(j\mid J_{m},H_{m},X_{m},\vec{p}_{m},I_{m},\left\{ \vec{\nu}_{im}\right\} _{i\in I_{m,}}\right)\mid I_{m},J_{m},H_{m},X_{m},\vec{p}_{m}\right]\!, \end{array} $$

where the second-to-last equality is from the law of iterated expectations and the last equality uses the definition of a choice probability that integrates out consumer product specific error terms of the form ε _ijm and product specific error terms of the form ξ _jm .

First consider the “if” direction. Consider two products j and k in the same nest h, and let $x_{jm}^{\prime}\beta-p_{jm}>x_{km}^{\prime}\beta-p_{km}$. Under Assumption 1, Lemma 1 states that

$$ \begin{array}{lll} &&\mbox{Pr}_{im}\left(j\mid J_{m},H_{m},X_{m},\vec{p}_{m},I_{m},\left\{ \vec{\nu}_{im}\right\} _{i\in I_{m,}}\right)\\&&{\kern1pc} >\mbox{Pr}_{im}\left(k\mid J_{m},H_{m},X_{m},\vec{p}_{m},I_{m},\left\{ \vec{\nu}_{im}\right\} _{i\in I_{m,}}\right) \end{array} $$

for all consumers. By the above market share algebra,

$$ \begin{array}{lll} &&{\kern2pt} E\left[s_{jm}\mid I_{m},J_{m},H_{m},X_{m},\vec{p}_{m}\right]\\ &&{\kern1pc}=\!\frac{1}{I_{m}}\!\sum\limits_{i=1}^{I_{m}}\!E\left[\mbox{Pr}_{im}\left(j\mid J_{m},H_{m},X_{m},\vec{p}_{m},I_{m},\left\{ \vec{\nu}_{im}\right\} _{i\in I_{m,}}\right)\mid I_{m},J_{m},H_{m},X_{m},\vec{p}_{m}\right]\\ &&{\kern1pc}>\!\frac{1}{I_{m}}\!\sum\limits_{i=1}^{I_{m}}\!E\left[\mbox{Pr}_{im}\left(k\mid J_{m},H_{m},X_{m},\vec{p}_{m},I_{m},\left\{ \vec{\nu}_{im}\right\} _{i\in I_{m,}}\right)\mid I_{m},J_{m},H_{m},X_{m},\vec{p}_{m}\right]\\&&{\kern1pc}=E\left[s_{km}\mid I_{m},J_{m},H_{m},X_{m},\vec{p}_{m}\right], \end{array} $$

as by Lemma 1 each consumer chooses j more often than k. As $E\left[s_{jm}\mid I_{m},\right.$ $\left.J_{m},H_{m},X_{m},\vec{p}_{m}\right]>E\left[s_{km}\mid I_{m},J_{m},H_{m},X_{m},\vec{p}_{m}\right]$ for any number of consumers I _m , $E\left[s_{jm}\mid J_{m},H_{m},X_{m},\vec{p}_{m}\right]>E\left[s_{km}\mid J_{m},H_{m},X_{m},\vec{p}_{m}\right]$ unconditional on the unobserved (in our data) number of consumers I _m .

The “only if” direction just reverses these documents, as the only way the sum of choice j’s probabilities can be greater than choice i’s under Lemma 1 is when $x_{jm}^{\prime}\beta-p_{jm}>x_{km}^{\prime}\beta-p_{km}$.

1.3 A.3 Lemma 3

Drop the m index for simplicity. We are comparing products j and k, which are in the same nest. The rank of product j with a finite sample of I customers is $\hat{r}_{j}$. The rank orders the (unobserved) market shares s _j . The condition that $\hat{r}_{j}>\hat{r}_{k}$ can be rewritten as $\hat{s}_{j}>\hat{s}_{k}$. Dividing by a positive number $\hat{s}_{j}+\hat{s}_{k}$, the inequality becomes

$$ \frac{\hat{s}_{j}}{\hat{s}_{j}+\hat{s}_{k}}>\frac{\hat{s}_{k}}{\hat{s}_{j}+\hat{s}_{k}}.$$

Define $\tilde{s}$ to be $\frac{\hat{s}_{j}}{\hat{s}_{j}+\hat{s}_{k}}$ , leaving $1-\tilde{s}$ to be $\frac{\hat{s}_{k}}{\hat{s}_{j}+\hat{s}_{k}}$. We want to show that $P\left(\tilde{s}>\frac{1}{2}\right)>P\left(\tilde{s}<\frac{1}{2}\right)$.

First consider the case without product market error terms ξ _j . We also condition on I _jk , the number of people who buy either j or k. An individual i prefers j over k with probability q _i . By Lemma 1, $q_{i}>\frac{1}{2}$. However, because the density of errors and the realization of fixed effects vary across consumers, q _i will be different for each consumer. We work with the number (rather then the fraction) of consumers who buy j out of the group who buy either j or k. Call this number r _j . The random variable r _k  = I _jk  − r _j is the number of consumers who pick k over j. Let $r^{\star}=\frac{I_{jk}}{2}$. We want to show $\mbox{Pr}\left(r_{j}>r^{\star}\right)>\mbox{Pr}\left(r_{k}>r^{\star}\right)$.

Now, if $q_{i}=\frac{1}{2}$ for all i, $\mbox{Pr}\left(r_{j}>r^{\star}\right)=\mbox{Pr}\left(r_{k}>r^{\star}\right)$ by the properties of the binomial distribution. By a monotonicity arguments, increasing even one q _i will raise $\mbox{Pr}\left(r_{j}>r^{\star}\right)$ and consequently weakly lower $\mbox{Pr}\left(r_{k}>r^{\star}\right)$, as for odd I _jk $\mbox{Pr}\left(r_{j}>r^{\star}\right)+\mbox{Pr}\left(r_{k}>r^{\star}\right)=1$ and for even I _jk $\mbox{Pr}\left(r_{j}>r^{\star}\right)+\mbox{Pr}\left(r_{k}>r^{\star}\right)=1-\mbox{Pr}\left(r_{k}=r_{j}\right)$. So $\mbox{Pr}\left(r_{j}>r^{\star}\right)>\mbox{Pr}\left(r_{k}>r^{\star}\right)$, and the “only if” direction of the lemma is proved. The “if” direction just reverses the above steps, as the only way one product is ranked higher than another more frequently is when the first product has a higher payoff.

The above argument conditioned on a value of I _jk . As the lemma holds for any value of I _jk , it holds unconditionally as well.

Now consider the case with both ξ _j and ε _ij errors. For each realization of ξ _j , each consumer has a q _i that involves the remaining uncertainty over the ε _ij terms. Even if j has a higher mean payoff than k, it could be that $q_{i}<\frac{1}{2}$ because of the realization of ξ _j and ξ _k . The probability q _i is the probability of picking j over k given that the payoff of j is $x_{j}^{\prime}\beta-p_{j}+\xi_{j}+\nu_{ih}$ and the payoff of k is $x_{k}^{\prime}\beta-p_{k}+\xi_{k}+\nu_{ih}$. By Lemma 1, $q_{i}>\frac{1}{2}$ when $x_{j}^{\prime}\beta-p_{j}+\xi_{j}+\nu_{ih}>x_{k}^{\prime}\beta-p_{k}+\xi_{k}+\nu_{ih}$. In other words, either the realization of product and market specific shocks is such that $q_{i}>\frac{1}{2}$ for everyone or $q_{i}\leq\frac{1}{2}$ for everyone. So the lemma being proved holds if $x_{j}^{\prime}\beta-p_{j}+\xi_{j}>x_{k}^{\prime}\beta-p_{k}+\xi_{k}$ more than half of the time when $x_{j}^{\prime}\beta-p_{j}>x_{k}^{\prime}\beta-p_{k}$, which it does because Assumption 1 states that the ξ’s are i.i.d.

1.4 A.4 Lemma 4

Our identification under sampling error argument will show that the probability limit of $Q_{M}\left(\beta\right)$ is uniquely maximized by the parameter vectors in the identified set B ⁰, which is defined in the statement of the lemma. Use the notation r _j for the underlying random variable for market share ranks. If M→ ∞, the maximum score objective function converges to the population objective function

$$ Q_{\infty}\left(\beta\right)=\sum\limits_{h=1}^{H}\sum\limits_{j,k\in J_{h},k\neq j}1\left[x_{j}^{'}\beta-p_{j}>x_{k}^{'}\beta-p_{k}\right]\cdot E\left\{ 1\left[r_{j}>r_{k}\right]\right\} ,\label{eq: probability limit}$$

(15)

where we have factored the fixed-across-markets product characteristics out of the expectation over the preferences of customers and the number of such customers in each market m. The probability limit can be rewritten to focus on unique pairs of products as

$$ \begin{array}{lll} Q_{\infty}\left(\beta\right)&=&\sum\limits_{h=1}^{H}\sum\limits_{j,k\in J_{h},k>j}\left\{ 1\left[x_{j}^{'}\beta-p_{j}>x_{k}^{'}\beta-p_{k}\right]\cdot E\left\{ 1\left[r_{j}>r_{k}\right]\right\}\right.\\ &&{\kern55.5pt} \left. +1\left[x_{k}^{'}\beta-p_{k}>x_{j}^{'}\beta-p_{j}\right]\cdot E\left\{ 1\left[r_{k}>r_{j}\right]\right\} \right\} . \end{array} $$

For each pair of products, the objective function is the sum of two probabilities times mutually exclusive inequalities. $Q_{\infty}\left(\beta\right)$ is maximized if the inequality multiplying the (weakly) greater of $E\left\{ 1\left[r_{j}>r_{k}\right]\right\}$ and $E\left\{ 1\left[r_{k}>r_{j}\right]\right\}$ is set to 1. Lemma 3 shows that $E\left\{ 1\left[r_{j}>r_{k}\right]\right\}$ is larger than $E\left\{ 1\left[r_{k}>r_{j}\right]\right\}$ precisely when $x_{j}^{'}\beta^{0}-p_{j}$ is greater than $x_{k}^{'}\beta^{0}-p_{k}$. Therefore, $Q_{\infty}\left(\beta\right)$ is maximized for any β ∈ B ⁰, the identified set. Clearly β ⁰ ∈ B ⁰, the identified set.

For identification under sampling error, we also need to show that parameter vectors that are not part of the identified set do not maximize the objective function. Equivalently, we need to prove that if some β maximizes $Q_{\infty}\left(\beta\right)$ then β ∈ B ⁰. If β maximizes $Q_{\infty}\left(\beta\right)$, the larger of $E\left\{ 1\left[r_{j}>r_{k}\right]\right\}$ and $E\left\{ 1\left[r_{k}>r_{j}\right]\right\}$ enters the objective function for each pair of choices. That term multiplies one of the mutually exclusive indicator functions in β, so this β must maximize the non-sampling error objective function, (6). So by the definition of B ⁰ and Lemma 3, β ∈ B ⁰ and the identified set comprises the maximizers of the probability limit of the objective function under sampling error.