1 Introduction

Quantum information is a fast developing and promising research area that combines ideas from information theory, computer science, and quantum physics [1]. The output of the quantum information field has the potential to foster advances in various fields, from quantum computing and novel devices to simulations of quantum dynamics [2]. The building of a quantum logic device necessitates good physical implementation of qubits and in-depth knowledge of how to manipulate them. The ability to control and measure qubit states should be accompanied by a high degree of qubit insulation from the environment to prevent decoherence. From the perspective of storing and manipulating quantum information, nuclear spins are attractive due to their long coherence times and well-developed nuclear magnetic resonance (NMR) techniques of the control of spin state and realization of logic gates [3]. Experimentally, quantum logic gates were first implemented using liquid-state NMR of small molecules with several spin 1/2 nuclei where a spin 1/2 was considered as a qubit [3, 4]. Different chemical shifts or gyromagnetic ratios of the nuclei allow these qubits to be addressed individually, and scalar couplings of the spins provide nonlinearity for the realization of logic operations using several qubits. Then, significant progress has been made in the quality of coherent control and in system complexity [5]. The experiments with a 12-qubit system [6,7,8] constitute the sole example of a large coherently manipulated quantum system with individually addressed qubits. Nuclear spins are being considered for long-term quantum information storage in combination with electronic spins and optical devices. Despite considerable progress, nuclear spin systems are still not sufficiently large, and their coherence times are not sufficiently long to be applied for realization of practical computation.

The possibility of realization of the logical gates using the quantum states of a single nucleus with a spin I > 1/2 was theoretically predicted in [9, 10] and the logical operations were experimentally realized in [11]. Recently, using the Kronecker products of the Pauli matrices, we have shown that the operators and Hamiltonians for nuclear quadrupole spins 3/2 and 7/2 can be represented in terms of a system of coupling fictitious spins 1/2, each of which can be considered as a qubit [12,13,14].

The representation of a spin 3/2 or 7/2 as a system of fictitious spins allows us to study quantum and classical correlations between qubits formed by these spins [12,13,14]. Quantum correlations, such as entanglement, were prominent in recent debates on the foundations of quantum mechanics. Entanglement is considered as a physical resource that plays a crucial role in quantum computing, quantum teleportation, and quantum key distribution [15, 16]. We predicted the unusual magnetic field dependencies of the classical and quantum correlations between the fictitious spins [12,13,14]. It was particularly shown, that, unlike the predictions of the Ising, Heisenberg, and dipole–dipole coupling spin models, the quantum mutual information, classical correlations, entanglement, and quantum discords between the fictitious spins do not vanish with an increase in magnetic field (the correlations tend to their limit values in high fields) [13, 14].

It should be noted that the aforementioned approach, the representations of a spin 3/2 as a system of two fictitious spins 1/2 and a spin 7/2 as a system of three fictitious spins 1/2, were used to implement the quantum gates. The feasibility of quantum computing is demonstrated with examples of constructing a controlled-NOT logic gate using the resonance excitation technique and SWAP and NOT2 logic gates using the level crossing method [15, 16].

The nonlocality measures provide a novel classification scheme for bipartite states and nonlocality is a quantum resource quite different from entanglement [17 and references therein].

Here we investigate generating three-qubit Bell nonlocality as the information resource in a three-qubit system created by the fictitious spins for a spin 7/2. We also compare the dependence of the Bell nonlocality measure on temperature and magnetic field with these dependencies of concurrence and geometrical discord.

The paper structure is the following. In the next section, the spin operators and the Hamiltonian for a spin 7/2 are represented in the operator terms for a system of three coupling fictitious spins 1/2, interacting qubits. In Sect. 3 the used calculation methods for quantum correlation measures are briefly presented. The dependencies of correlation measures (concurrence, geometrical discord, and nonlocality indicator, so-called MIN [17]) on temperature and magnetic field are analyzed and compared in Sect. 4. In the last section, we conclude our results.

2 Representation of a spin 7/2 as a fictitious spin 1/2 system

For the convenience of readers, we briefly describe a representation of a spin 7/2 by a three fictitious spin 1/2 system. In consideration of spins larger than 1/2, it proves often convenient to use the formalisms of fictitious spins 1/2 [18,19,20,21] and of projection operators [22]. In these works, the fictitious spin operators of nuclear spins 1 and 3/2 were represented by the 3 × 3 and 4 × 4 operators, respectively. The fictitious spin operators are presented as a superposition of block matrices in which the blocks are Pauli matrices.

Here we will use another approach, in which the spin 3/2 was represented as a system of two effective 1/2 spins [21]. In the present paper, nuclear spin 7/2 is presented as a system of three spins 1/2 [14]. The Hamiltonian and all operators for spin 7/2 are represented as a superposition of the orthonormal 64 direct products (\(\sigma_{k} \otimes \sigma_{m} \otimes \sigma_{n} {\text{ with }}k,\,n,\,m = 0,\,x,\,y,\,z\)) of three Pauli and unit matrices: \(\sigma_{x} ,\;\sigma_{y} ,\;\sigma_{z} \, \) and \(\sigma_{0} \, \), respectively. So, the consideration of a spin 7/2 can be replaced by the consideration of a system of three fictitious spins 1/2. From a quantum information perspective, the states of spin 7/2 can be viewed as the states of interacting qubits created by these three fictitious spins [14].

The Hamiltonian of the nuclear spin I = 7/2 placed in an axial electric field gradient (EFG) and an external magnetic field \(\vec{H}_{0} = \{ H_{0x} ,\,H_{0z} ,\,H_{0z} \}\) in the principal axis frame of EFG ( \(\left| {V_{zz} } \right| \ge \left| {V_{yy} } \right| \ge \left| {V_{xx} } \right|\,\)) has the following form (we used units where \(\hbar = 1\)):

$$ H = H_{Z} + H_{Q} ,\, $$
(1)

where the Zeeman Hamiltonian \(H_{{{\text{Zeem}}}}\) describes the interaction of the nuclear spin with the external magnetic field

$$ H_{{{\text{Zeem}}}} = - \gamma \left( {H_{x} I_{x} + H_{y} I_{y} + H_{z} I_{z} } \right)\,, $$
(2)

where \(\gamma\) is the nuclear gyromagnetic ratio and \(I_{i}\) \(\left( {i = x,\,y,\,z} \right)\) is the projections of the spin angular momentum operator \(\vec{I}\) on the x -, y -, and z-axes. The Hamiltonian \(H_{Q}\) represents the interaction of the spin with EFG and is given by

$$ H_{Q} = \omega_{Q} \left[ {3I_{z}^{2} - \vec{I}^{2} + \eta \left( {I_{x}^{2} - I_{y}^{2} } \right)} \right],\, $$
(3)

where \(\omega_{Q} = \tfrac{{e^{2} Qq}}{{4I\left( {2I - 1} \right)}}\) is the quadrupole frequency and the asymmetry parameter \(\eta\) is defined as

$$ \eta = \frac{{V_{yy} - V_{xx} }}{{V_{zz} }},\, $$
(4)

and may vary between 0 and 1.

Introducing the fictitious spin 1/2 operators similarly to the spin 1/2 operators in a system of three real spins 1/2

$$ I_{\zeta 1} = \left( {\sigma_{\zeta } \otimes \hat{e}} \right) \otimes \hat{e},\, \, I_{\zeta 2} = \left( {\hat{e} \otimes \sigma_{\zeta } } \right) \otimes \hat{e},\,{\text{ and }}I_{\zeta 3} = \left( {\hat{e} \otimes \hat{e}} \right) \otimes \sigma_{\zeta } ,\, \, \zeta = x,\,y,\,z{ ,} $$

we can rewrite the spin 7/2 operators Ix, Iy, Iz, and Hamiltonian (3) as [14]

$$ \begin{aligned} I_{x} & = \frac{1}{4}\left( {\sqrt 7 + \sqrt {15} } \right)\,I_{{x3}} + \frac{{\sqrt 3 }}{2}\left( {I_{{x2}} I_{{x3}} + I_{{y2}} I_{{y3}} } \right)\, \\ & \quad + \frac{1}{2}\left( {I_{{x1}} I_{{x2}} I_{{x3}} + I_{{y1}} I_{{y2}} I_{{x3}} + I_{{y1}} I_{{x2}} I_{{y3}} - I_{{x1}} I_{{y2}} I_{{y3}} } \right) - \frac{1}{4}\left( {\sqrt {15} - \sqrt 7 } \right)\,I_{{z1}} I_{{z2}} I_{{x3}} , \\ I_{y} & = \frac{1}{4}\left( {\sqrt 7 + \sqrt {15} } \right)\,I_{{y3}} + \frac{{\sqrt 3 }}{2}\left( {I_{{y2}} I_{{x3}} - I_{{x2}} I_{{y3}} } \right) \\ & \quad - \frac{1}{2}\left( {I_{{x1}} I_{{x2}} I_{{y3}} + I_{{x1}} I_{{y2}} I_{{x3}} - I_{{y1}} I_{{x2}} I_{{x3}} + I_{{y1}} I_{{y2}} I_{{y3}} } \right)\, - \frac{1}{4}\left( {\sqrt {15} - \sqrt 7 } \right)\,I_{{z1}} I_{{z2}} I_{{y3}} , \\ I_{z} & = 2I_{{z1}} + I_{{z2}} + \frac{1}{2}I_{{z3}} , \\ \end{aligned} $$
(5)
$$ \begin{aligned} H_{Q} & = \frac{{Qqe^{2} }}{7}\left\{ {I_{z1} I_{z2} + \frac{1}{2}I_{z1} I_{z3} + \frac{1}{4}I_{z2} I_{z3} + } \right. \\ & \left. {\frac{\eta }{24}\left[ {\left( {3\sqrt 5 + \sqrt {21} } \right)\,I_{x2} + 2\sqrt {15} \left( {I_{x1} I_{x2} + I_{y1} I_{y2} } \right) + \left( { - 3\sqrt 5 + \sqrt {21} } \right)\,I_{z1} I_{x2} I_{z3} } \right]} \right\} \\ \end{aligned} $$
(6)

The Zeeman Hamiltonian \(H_{{{\text{Zeem}}}}\) (2) where a DC magnetic field is applied along the x-, y-, and z-axes is, respectively:

$$ H_{ZX} = - \gamma H_{x} I_{x} $$
(7)
$$ H_{ZY} = - \gamma H_{y} I_{y} $$
(8)
$$ H_{ZZ} = - \gamma H_{z} I_{z} $$
(9)

Equations (5–8) demonstrate the pair- and three-body interactions between the fictitious spins, and the strengths of these interactions depend on the applied field as opposed to real spin systems where these interactions are independent of an applied magnetic field and determined by the internal characteristics of the spin system [23].

The density matrix can be presented in the following form [23]:

$$ \rho = Z^{ - 1} \exp \left( { - \frac{H}{{k_{{\text{B}}} T}}} \right), $$
(10)

where \(Z = Tr\left[ {\exp \left( { - \tfrac{H}{kT}} \right)} \right]\) is the partition function, T is the spin temperature, and \(k_{{\text{B}}}\) is the Boltzmann constant.

The calculation results in the paper will be presented using the following dimensionless parameters:

$$ \beta = \frac{{e^{2} Qq}}{{k_{B} T}}\;{\text{and}}\;\alpha_{i} = \frac{{\gamma H_{0i} }}{{e^{2} Qq}}\;{\text{with}}\;i = x,\;y,\;z $$
(11)

which characterize the ratios of the nuclear quadrupole to thermal energy and the Zeeman to the quadrupole energy, respectively. These parameters can be both positive and negative (for various nuclei the nuclear quadrupole moment \(Q\) can possess different signs [23] and \(\alpha {\kern 1pt}_{i} < 0\) in the ferromagnetic phase and \(\alpha {\kern 1pt}_{i} > 0\) in the antiferromagnetic phase).

3 Correlation measures

The quantum correlations in a multi-spin 1/2 system can be characterized by measures of the correlations between various two spins. The state of two spins selected from the whole spin system can be given by the corresponding reduced density 4 × 4 matrix [24, 25]. This allows us to use well-known methods to calculate the measures of correlations in a real two-spin 1/2 system [24,25,26,27]. Using this approach, we will consider concurrence, geometrical discord, and nonlocality in the fictitious spin 1/2 system representing a spin 7/2. For the m-th and n-th spins, the reduced density matrix \(\rho_{mn}\) is defined as \(\rho_{mn} = Tr_{mn} \left( \rho \right)\) where \(Tr_{mn} \left( {...} \right)\) denotes the trace over the degrees of freedom for all spins except the m-th and n-th spins.

3.1 Concurrence

We will characterize the pairwise entanglement by the concurrence between two, m-th and n-th, spins using the reduced matrix \(\rho_{mn}\) for these spins. Note that, in the general case, the reduced matrices describe the mixed states. Hence, the bipartite concurrences are defined as [27]

$$ C_{mn} = \mathop {\max }\limits \left\{ {q_{mn} ,\,0} \right\},\, $$
(12)

with \(q_{mn} = \lambda_{mn}^{\left( 1 \right)} - \lambda_{mn}^{\left( 2 \right)} - \lambda_{mn}^{\left( 3 \right)} - \lambda_{mn}^{\left( 4 \right)}\). Here \(\lambda_{mn}^{\left( k \right)} \quad \left( {k = 1,...,4} \right)\) are the square roots of eigenvalues, in descending order, of the following non-Hermitian matrix:

$$ R_{mn} = \rho_{mn} \left( {\sigma_{y} \otimes \sigma_{y} } \right)\,\tilde{\rho }_{mn} \left( {\sigma_{y} \otimes \sigma_{y} } \right),\, $$
(13)

In Eq. (13) \(\tilde{\rho }_{mn}\) is the complex conjugation of the reduced density matrix \(\rho_{mn}\).

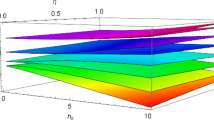
Figure 1 presents dependences of concurrence on β and αx at η = 0.5 between the 1th and 2nd spins, between the 1th and 3rd spins, and between the 2th and 3rd spins.

Fig. 1
figure 1

Dependences of concurrence on β and αx: a between the 1th and 2nd spins; b between the 1th and 3rd spins; c between the 2nd and 3rd spins. Magnetic field is parallel to the x-axis and η = 0.5

Full size image

3.2 Geometric discord

The authors of [28] introduced the geometric measure of the quantum discord (geometric discord) as the minimal square norm in the Hilbert–Schmidt space between the two-qubit and the zero-discord states. Any reduced density 4 × 4 matrix can be rewritten in the Bloch representation:

$$ \rho_{mn} = \frac{1}{4}\left( {\sigma_{0} \otimes \sigma_{0} + \sum\limits_{\zeta } {x_{\zeta } \sigma_{\zeta } \otimes \sigma_{0} } + \sum\limits_{\zeta } {y_{\zeta } \sigma_{0} \otimes \sigma_{\zeta } } + \sum\limits_{\zeta ,\xi } {t_{\zeta ,\xi } \sigma_{\zeta } } \otimes \sigma_{\xi } } \right) $$
(14)

where \(x_{\zeta } = tr\left[ {\rho_{mn} \left( {\sigma_{\zeta } \otimes \sigma_{0} } \right)} \right]\) and \(y_{\zeta } = tr\left[ {\rho_{mn} \left( {\sigma_{0} \otimes \sigma_{\zeta } } \right)} \right]\) are the components of the local Bloch vectors, \(t_{\zeta ,\xi } = tr\left[ {\rho_{mn} \left( {\sigma_{\zeta } \otimes \sigma_{\xi } } \right)} \right]\) are the components of the correlation tensor, the indexes \(\zeta {\text{ and }}\xi = x,\;y,\;z.\)

The two-qubit system is considered as a system containing two subsystems A and B. In the general case, a measure of the geometric discord depends on the subsystem relative to which the measurement is done [13]. Now using the Bloch representation (14) for the reduced density matrix the discord \(d_{{{\text{GA}}}}\) relative to the measurements on subsystem A (one of the considered qubits) is [27]:

$$ d_{{{\text{GA}}}} = \frac{1}{4}\left( {\left\| x \right\|^{2} + \left\| t \right\|^{2} - \lambda_{\max }^{\left( A \right)} } \right) $$
(15)

and the discord \(d_{{{\text{GB}}}}\) relative to the measurements on subsystem B (second qubit) is [28]:

$$ d_{{{\text{GB}}}} = \frac{1}{4}\left( {\left\| y \right\|^{2} + \left\| t \right\|^{2} - \lambda_{\max }^{\left( B \right)} } \right) $$
(16)

where \(\left\| X \right\|^{2} = trX^{2} = tr\left( {XX^{T} } \right)\) is the square norm; the matrices \(t = \left\{ {t_{\zeta ,\xi } } \right\}\), \(x = \left\{ {x_{\zeta } } \right\}\), \(y = \left\{ {y_{\zeta } } \right\}\); \(\lambda_{\max }^{\left( A \right)}\) and \(\lambda_{\max }^{\left( B \right)}\) are the largest eigenvalues of matrices \(xx^{T} + tt^{T}\) and \(yy^{T} + tt^{T}\), respectively.

For the considered two-qubit systems, a little difference (several percents) between \(d_{GA}\) and \(d_{GB}\) was obtained, and here we present results of calculation \(d_{GA}\) (Fig. 2).

Fig. 2
figure 2

Dependences of geometric discord on β and αx: a between the 1th and 2nd spins; b between the 1th and 3rd spins; c between the 2nd and 3rd spins. Magnetic field is parallel to the x-axis and η = 0.5

Full size image

The geometric discords given by Eqs. (14) and (15) are not normalized to 1 [28]: Their maximum values are ½ for a two-qubit system. Following [29], below the normalized geometric discord \(D_{GA} = 2d_{GA}\) with the maximum of 1 will be considered for comparison with other quantum correlations.

3.3 Bell nonlocality

Here to indicate two-qubit nonlocality we will use a measurement of, so-called MIN, quantity \(N\) which defined as the maximum of square norm in the Hilbert–Schmidt space between the pre- and the post-measurement states [17]. The analytical expression for \(N_{A}\) relative to the measurements on subsystem A has been obtained for a two-qubit system [17, 30]:

$$ N_{A} = \frac{1}{4}\left\{ {\begin{array}{*{20}c} {tr\left( {tt^{T} } \right) - \frac{1}{{tr\left( {xx^{T} } \right)}}x^{T} tt^{T} x} & {x \ne 0} \\ {tr\left( {tt^{T} } \right) - \lambda_{\min } } & {x = 0} \\ \end{array} } \right. $$
(17)

where \(\lambda_{\min }\) is the minimum eigenvalue \(tt^{T}\), the matrix \(tt\) and vectors \(x\) and \(y\) are given by the Bloch representation (14).

Note that the Bloch representation (14) for the density matrix somewhat differs from the representation in the Hermitian bases used in [30, Eq. (3)]. The difference manifests itself in different values of matrices \(tt\) and vectors \(x\) and \(y\). To compensate for this difference, a coefficient of ¼ is introduced in (16). The authors of [17] used representation (14) and expression (17) without the coefficient. This leads to different MIN values being determined in [30], and here using (17): The maximum MIN in [17] and here is 0.5, but in [30] is 2. To overcome this difference, we propose to use the normalized MIN with a maximum of 1. In our case \(N = 2N_{A}\) will be analyzed (Fig. 3).

Fig. 3
figure 3

Dependences of MIN on β and αx: a between the 1th and 2nd spins; b between the 1th and 3rd spins; c between the 2nd and 3rd spins. Magnetic field is parallel to the x-axis and η = 0.5

Full size image

4 Results and discussion

Representation of the Hamiltonian and spin operators for a spin 7/2 in the basic of the orthonormal direct products of three Pauli and unit matrices established that the spin 7/2 quantum states can be considered as states of three fictious spins 1/2, interacting qubits (Sect. 2 and, e.g. [14]). This allows us to study nonlocality in the qubit system and compare it with other quantum correlations using the method developed for real spin systems. This approach was applied to analysis correlation in the two fictious spin system representing a spin 3/2 [12, 16, 33]

We first obtained that in the system of three interacting fictitious spins 1/2, which represents a spin 7/2, there is nonlocal correlation, measure of nonlocality, MIN, is nonzero. The correlations between various spin (qubit) pairs were analyzed. A real distance between these fictitious spins cannot be determined. However, the two-qubit Bell nonlocality in the fictitious spin system can be considered as a new two-qubit information resource.

Hamiltonians (6)–(9) contain the terms describing interaction between the fictitious spins. A finite strength of the interaction can be formally (mathematically) considered as an interaction between spins located at a finite distance between each other. The interaction between the fictitious spins depends on the magnetic field. If magnetic field is absent the Hamiltonian contains terms describing the pair-spin and three-spin interactions which depend on the asymmetry parameter.

The calculation results when the external magnetic field is directed along the x- axis or y-axis are about the same. If the field is directed along the z-axis zero concurrency is obtained. For different values of the asymmetry parameter \(\eta\) the results of the correlation calculation are somewhat different, but the dependences do not differ qualitatively: The increase in the parameter from 0 to 1 leads to grow of the correlation measures less than percents. Below we consider the results at \(\eta = 0.5\) in the magnetic field directed along the x-axis.

The values of the correlation measures strongly depend on the considered pair of fictious spins: e.g. nonlocality between the 1th and 2nd spins achieves 0.6, between the 1th and 3rd spins—0.1, at the same time, nonlocality between the 2nd and 3rd spins is negligible small (less than 0.03). The last can be explained by the structures of reduced matrices (Fig. 4). The elements placed on the diagonals of the matrix for a two-spin 1/2 system, represented in the basic of the system state, mainly determine concurrence. Indeed, the strongest correlation arise between the 1th and 2nd spins, less strong between the 1th and 3rd spins, and, finally, very weak between the 2nd and 3rd spins.

Fig. 4
figure 4

Block diagrams for the reduced density matrix \(\rho_{mn}\): a the 1th and 2nd spins, \(\rho_{12}\); (b) the 1th and 3rd spins, \(\rho_{13}\); c the 2nd and 3rd spins,\(\rho_{23}\)

Full size image

The magnetic field and temperature dependences of the quantum correlations between the 2nd and 3rd spins differ qualitatively and quantitatively from these correlations’ dependences for other spin pairs. The measures of the correlations between the 2nd and 3rd spins are significantly less and possess the maxima; while, the behavers of the measures for other pairs are qualitatively the same; they monotonically increase with a magnetic field and the parameter \(\beta\).

Here we more detailed consider correlations between the 1st and 2nd spins. Magnetic field dependencies of all correlations are symmetrical (Figs. 1, 2 and 3). The correlation dependences on the parameter \(\beta\) are also close to symmetrical; however, the correlation measures are some less at \(\beta < 0.\)

One can see that in the \(\beta - \alpha_{x}\) plan (Fig. 5) the area where a concurrence value is significant is smallest and the largest area is for nonlocality measure.

Fig. 5
figure 5

Contour plots of concurrence (a), quantum discord (b) and nonlocality (c) for the 1th and 2nd spins. Here \(\eta = 0.5\) and contour level 0.05. Dark blue denotes the areas where the correlations are negligible

Full size image

In low magnetic field and at small parameter \(\beta\) the correlations are absent. With an increase in \(\left| \beta \right|\) and magnetic field the correlations appear and monotonically increase. The monotonical increase nonlocality measure with magnetic field is disturbed at \(\beta < - 2\) where the local maximum appears (Fig. 5c). In this case, a finite nonlocality measure is observed in zero magnetic field. A finite nonlocality is observed also in zero magnetic field at a high \(\beta > 0\) in opposite to concurrence and discord which appear in noticeable magnetic fields. This can be explained by existence of the term in the quadrupole Hamiltonian \(H_{Q}\) (6) describing the Zeeman type of interaction (term \(\frac{{Qqe^{2} \eta }}{{{168}}}\left( {3\sqrt 5 + \sqrt {21} } \right)I_{x2}\)).

The second reason is that spin interaction leads to the appearance of nonlocal correlation between the fictitious spins when the spin 7/2 is in a zero magnetic field, even though concurrence and discord are zero.

The differences between the temperature–magnetic field ranges for existence of concurrence, geometrical discord and nonlocality, as well as other quantum and classical correlations were discussed early for a real and fictitious spins representing a spin 3/2 (see, e.g. [13, 17, 30,31,32,33] and references therein).

The appearance of the nonlocal correlation, where other quantum correlations are absent, in real two-spin 1/2 systems were predicted in [17, 31]. The authors of [30] studied nonlocal correlation using Heisenberg models for real spin 1/2 systems and showed that nonlocal correlation (finite MIN value) and discord can be observed in such systems even when concurrence is zero. In [32] the Bell nonlocality was considered using the two-spin Heisenberg XYZ model and the two-qubit Bell function as an indicator of nonlocality [33, 34]. In contrast to our results in [17, 30, 35] it was showed that concurrence can be nonzero when magnetic field is absent.

As an example to possibly access the quantum correlations can be considered a quadrupole nucleus 59Co (I = 7/2 and 100% abundance) in the compound [Co(NH3)5Cl]Cl2 [36] at αx = 1, η = 0.215 and Qqzze2 = 31.74 MHz gives that the concurrence appears at β = 0.64 (Fig. 6). This β value corresponds to temperature T≈ 2.4 mK.

Fig. 6
figure 6

Dependence of concurrence between the 1th and 2nd on β at η = 0.215 and αx = 1

Full size image

Another example is single crystals of Ca3Co2O6 [37]. 59Co NMR measurements were performed on a single crystal in a temperature range, 2–300 K, under a fixed magnetic field, H0 = 9.4026 T [37]. We estimate that at αx = 1 and η = 0 the entangled state appears at β = 0.64 also. It has been shown [38,39,40,41,42] that for the XY and dipolar coupling spin 1/2 systems entanglement appears at very low temperatures T≈ 0.3–0.5 μK. This value is four orders smaller than the value estimated by us for a quadrupole system. Solid-state systems containing, for instance, 51V, 165Ho, or 123Sb, whose nuclear spins are 7/2 [43,44,45], can be considered as samples for studying quantum correlations in the three-fictitious-spin system.

5 Conclusion

In literature classical and various quantum correlations such as entanglement, quantum and geometrical discords, nonlocality, have been studied in real spin 1/2 systems. We first investigated the temperature and field dependences of nonlocality measure, MIN, in the fictitious spin 1/2 system, which represents a nuclear spin 7/2 placed in magnetic and inhomogeneous electric fields, and relationship between nonlocality and other quantum correlations (entanglement and geometric discord). From the quantum information point of view the states of these spins 1/2 can be considered as three interacting qubits. The representation using fictious spins makes it possible to apply to their system under consideration well-developed methods [13, 14, 25,26,27,28] for calculating correlation measures.

It was shown that nonlocality can appear under conditions where entanglement and geometric discord are absent, that allows assuming that the quantum correlation is more general than the other. The two-qubit Bell nonlocality in a fictitious spin system can be considered as a new information resource quite different from entanglement.