Abstract
The disrupting effect of quantum memory on the dynamics of a spatial quantum formulation of the iterated prisoner’s dilemma game with variable entangling is studied. The game is played within a cellular automata framework, i.e., with local and synchronous interactions. The main findings of this work refer to the shrinking effect of memory on the disruption induced by noise.








Similar content being viewed by others
Notes
\(\gamma ^\star _{0.0,0.0}\!=\!\arcsin \left( \sqrt{\frac{P-S}{\mathfrak {T}-S}=\frac{1}{4}}\right) =\frac{\pi }{6} \simeq 0.524, \gamma ^\bullet _{0.0,0.0}\!=\!\arcsin \left( \sqrt{\frac{\mathfrak {T}-R}{\mathfrak {T}-S}=\frac{2}{4}}\right) =\frac{\pi }{4}\!\simeq 0.785\).
\(\gamma ^\star _{0.5,0.0}\!=\!2\arcsin \left( \sqrt{\frac{P-S}{2(\mathfrak {T}-S)}\!=\!\frac{1}{8}}\right) \!\simeq \!0.723, \gamma ^\bullet _{0.5,0.0}\!=\!2\arcsin \left( \sqrt{\frac{\mathfrak {T}-R}{2(\mathfrak {T}-S)}\!=\!\frac{2}{8}}\right) \!=\! \frac{\pi }{3} \simeq 1.047\).
From Eq. (6), it is \(p_B^{ \mathcal Q,\mathcal D(u)}(0)=\mathfrak {T}\cos ^2\gamma + S\sin ^2\gamma \) and \(p_{A,B}^{\mathcal Q,\mathcal C(u)}(0)=R\cos ^2\gamma + P\sin ^2\gamma \), whose equalization leads to \(\gamma ^\bullet _{0.0,0.0}=\arcsin \left( \sqrt{\frac{\mathfrak {T}-R}{\mathfrak {T}+P-R-S}}\right) = \arcsin \left( \sqrt{\frac{2}{3}}\right) \simeq 0.955\). In this scenario, it is \(\gamma ^\bullet _{0.5,0.0}=2\arcsin \left( \sqrt{\frac{P-S}{\mathfrak {T}+P-R-S}=\frac{1}{3}}\right) \simeq 1.231\).
It is \(\Pi ^{\hat{\mathcal M},\hat{U}(\theta _B, 0)}_{u}(0)\!=\!\displaystyle \frac{1}{2} \left( \begin{matrix} 0 &{} 0\\ 1-\sin \theta _B &{} 1+\sin \theta _B \end{matrix}\right) \), which renders \(p^{\hat{\mathcal M},\hat{U}(\theta _B, 0) }_{\left\{ \!\begin{array}{c}\!A\!\\ \!B \!\end{array}\!\right\} } (0, 0) =\displaystyle \frac{1}{2}\left[ \left\{ \!\begin{array}{c}\!\mathfrak {T}\\ \!S\end{array}\!\right\} (1-\sin \theta _B) +P(1+\sin \theta _B)\right] \). Consequently, \(p^{\hat{\mathcal M},\hat{U}(\theta _B, 0)}_{\left\{ \!\begin{array}{c}\!A\!\\ \!B \!\end{array}\!\right\} }(0,0)=P\) for \(\theta _B=\pi /2.\)
\(p^{\hat{\mathcal W},\hat{U}(\pi /2, 0)}_A(0,0)=\frac{1}{4}\left[ 11+\frac{3}{4}(2+\sqrt{2})\sin ^2\gamma -3\sqrt{2+\sqrt{2}}\sin \gamma \right] \), and \(p^{\hat{\mathcal W},\hat{U}(\pi /2, 0)}_B(0,0)=\frac{1}{4}\left[ 11-\frac{5}{4}(2+\sqrt{2})\sin ^2\gamma + \sqrt{2+\sqrt{2}}\sin \gamma \right] \). These payoffs are structurally similar to those generated by the \(\{\hat{\mathcal M},\hat{U}(\pi /2, 0)\}\) pair from \(\Pi ^{\hat{\mathcal M},\hat{U}(\pi /2, 0)} _u (0,0) =\frac{1}{4} \left( \begin{array}{cc}\cos ^2\gamma &{}\cos ^2\gamma \\ (\cos \frac{\gamma }{2}-\sin \frac{\gamma }{2})^4 &{} (\cos \frac{\gamma }{2}+\sin \frac{\gamma }{2})^4 \end{array}\right) \), which are equal to \(p^{\hat{\mathcal M},\hat{U}(\pi /2, 0)}_A(0,0)\!=\!\frac{1}{4}(11+ 3\sin ^2\gamma - 6\sin \gamma )\), and \(p^{\hat{\mathcal M},\hat{U}(\pi /2, 0)}_B(0,0)\!=\!\frac{1}{4}(11 - 5\sin ^2\gamma + 2\sin \gamma )\). In both games it is \(p_A^{\hat{\mathcal M},\hat{U}(\pi /2, 0)}(0,0)=p_B^{\hat{\mathcal M},\hat{U}(\pi /2, 0)}(0,0)=11/4\) at \(\gamma =0\), and \(p_B^{\hat{\mathcal M},\hat{U}(\pi /2, 0)}(0,0)>p_A^{\hat{\mathcal M},\hat{U}(\pi /2, 0)}(0,0)\), even for \(\gamma =\pi /2\) in the \(\{\hat{\mathcal W},\hat{U}(\pi /2, 0)\}\) game, whereas \(p_A^{\hat{\mathcal M},\hat{U}(\pi /2, 0)}(0,0)=p_B^{\hat{\mathcal M},\hat{U}(\pi /2, 0)}(0,0)=2\) in the \(\{\hat{\mathcal M},\hat{U}(\pi /2, 0)\}\) game.
It is \( \Pi ^{\mathcal M,\mathcal D}_u (0,0) = \frac{1}{2} \left( \begin{array}{cc} 0&{} \sin ^2\gamma \\ \cos ^2\gamma &{} 1\end{array}\right) \), which renders the payoffs \(p_{_{\texttt {A}}}^{\mathcal M,\mathcal D}(0, 0)= \frac{1}{2}\left[ (\mathfrak {T}-S)\sin ^2\gamma + P+S\right] ,\) and \(p_{_{\texttt {B}}}^{\mathcal M,\mathcal D}(0,0)= \frac{1}{2}\left[ (S-\mathfrak {T})\sin ^2\gamma + P+\mathfrak {T}\right] .\)
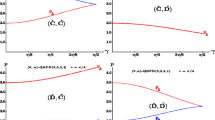
The values of \((p_A,p_B)\) at \(\gamma =\pi /2\) in the \((\hat{\mathcal M},\hat{\mathcal D})\) two-player game, and those of \((\overline{p}_A,\overline{p}_B)\) in the CA simulations of Fig. 3 are (from top to bottom): (3.125, 2.125), (3.042, 2.181); (3.203, 1.996), (3.110, 2.071); (3.280, 1.866), (3.166, 1.944).
References
Eisert, J., Wilkens, M., Lewenstein, M.: Quantum games and quantum strategies. Phys. Rev. Lett. 83(15), 3077–3080 (1999)
Alonso-Sanz, R.: On a three-parameter quantum battle of the sexes cellular automaton. Quantum Inf. Process. 12(5), 1835–1850 (2013)
Alonso-Sanz, R.: A quantum battle of the sexes cellular automaton. Proc. R. Soc. A 468, 3370–3383 (2012)
Huang, Z., Alonso-Sanz, R., Situ, H.: Quantum Samaritan’s dilemma under decoherence. Int. J. Theor. Phys. 56(3), 863–873 (2017)
Alonso-Sanz, R., Situ, H.: A quantum Samaritan’s dilemma cellular automaton. R. Soc. Open Sci. 4(6), 863–160669 (2017)
Ozdemir, S.K., Shimamura, J., Morikoshi, F., Imoto, N.: Dynamics of a discoordination game with classical and quantum correlations. Phys. Lett. A 333, 218–231 (2004)
Du, J.F., Li, H., Xu, X., Shi, M., Wi, J., Zhou, X., Han, R.: Experimental realization of quantum games on a quantum computer. Phys. Rev. Lett. 88(13), 137902 (2002)
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)
Ramzan, M., Nawaz, A., Toor, A.H., Khan, M.K.: The effect of quantum memory on quantum games. J. Phys. A Math. Theor. 41, 055307 (2008)
Owen, G.: Game Theory. Academic Press, Cambridge (1995)
Benjamin, S.C., Hayden, P.M.: Comment on “Quantum games and quantum strategies”. Phys. Rev. Lett. 87, 069801 (2001)
Benjamin, S.C., Hayden, P.M.: Multiplayer quantum games. Phys. Rev. A 64, 030301 (2001)
Eisert, J., Wilkens, M., Lewenstein, M.: Comment on “Quantum games and quantum strategies”—reply. Phys. Rev. Lett. 87, 069802 (2001)
Eisert, J., Wilkens, M.: Quantum games. J. Mod. Opt. 47(14–15), 2543–2556 (2000)
Alonso-Sanz, R.: Spatial correlated games. R. Soc. Open Sci. 4(6), 171361 (2017). https://doi.org/10.1098/rsos.171361
Zhang, S. (2012). Quantum strategic game theory. In: Proceedings of the 3rd Innovations in Theoretical Computer Science Conference (ITCS ’12). ACM, New York. ISBN: 978-1-4503-1115-1
Brunner, N., Linden, N.: Connection between nonlocality and Bayesian game theory. Nat. Commun. 4, 2057 (2013)
Pappa, A., Kumar, N., Lawson, T., Santha, M., Zhang, S., Diamanti, E., Kerenidis, I.: Nonlocality and conflicting interest games. Phys. Rev. Lett. 114, 020401 (2015)
Yin, J., et al.: Satellite-based entanglement distribution over 1200 kilometers. Science 356, 1140 (2017)
Schiff, J.L.: Cellular Automata: A Discrete View of the World. Wiley, London (2008)
Du, J.F., Xu, X.D., Li, H., Zhou, X., Han, R.: Entanglement playing a dominating role in quantum games. Phys. Lett. A 89(1–2), 9–15 (2001)
Du, J.F., Li, H., Xu, X.D., Zhou, X., Han, R.: Phase-transition-like behaviour of quantum games. J. Phys. A Math. Gen. 36(23), 6551–6562 (2003)
Alonso-Sanz, R.: On the effect of quantum noise in a quantum prisoner’s dilemma cellular automaton. Quantum Inf. Process. 16(6), 161 (2017)
Alonso-Sanz, R.: Variable entangling in a quantum prisoner’s dilemma cellular automaton. Quantum Inf. Process. 14(1), 147–164 (2015)
Alonso-Sanz, R.: A quantum prisoner’s dilemma cellular automaton. Proc. R. Soc. A 470, 20130793 (2014)
Flitney, A.P., Abbott, D.: Advantage of a quantum player over a classical one in \(2\times 2\) quantum games. Proc. R. Soc. Lond. A 459(2038), 2463–2474 (2003)
Flitney, A.P., Abbott, D.: Quantum games with decoherence. J. Phys. A Math. Gen. 38(2), 449 (2004)
Alonso-Sanz, R., Situ, H.: On the effect of quantum noise in a quantum relativistic prisoner’s dilemma cellular automaton. Int. J. Theor. Phys. 55(12), 5265–5279 (2016)
Alonso-Sanz, R., Situ, H.: On the effect of quantum noise in a quantum relativistic battle of the sexes cellular automaton. Phys. A 468, 267–277 (2016)
Alonso-Sanz, R.: Dynamical Systems with Memory. World Scientific, Singapore (2011)
Acknowledgements
This work has been funded by the Spanish Grant MTM2015-63914-P. Part of the computations of this work were performed in EOLO, an HPC machine of the International Campus of Excellence of Moncloa, funded by the UCM and Feder Funds.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
The thresholds for a fair quantum game played with the (5, 3, 2, 1)-PD parameters and a noise strength equal to \( \mu = 0.5\) are given as a function of the memory factor \(\eta \) by
For the unfair quantum versus classical case, the lowest threshold is given by Eq. (A.1a), while the largest one equals
Rights and permissions
About this article
Cite this article
Alonso-Sanz, R., Revuelta, F. On the effect of memory in a quantum prisoner’s dilemma cellular automaton. Quantum Inf Process 17, 60 (2018). https://doi.org/10.1007/s11128-018-1823-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-018-1823-z