1 Introduction

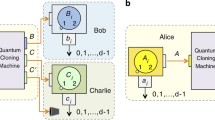
Soon after recognizing that quantum information can be neither perfectly copied [1] nor broadcasted [2], physicists have gone to any length to bypass this limitation. As it has been a struggle against nature, their efforts could be only partially successful [3, 4]. Possibility of quantum cloning, even though imperfect, has a great impact on security of quantum data transmission [5, 6]. References [7] and [8] can serve as two examples of reviews summarizing theoretical and practical achievements of quantum cloning. There are various types of cloning machines dedicated to cloning often very specific and special classes of states, but we focus our attention on the most elementary and fundamental universal quantum cloning machine (UQCM) [3] which in an ideal setting can clone equally effectively arbitrary states. Such a machine operates on three qubits: The first is the input which is to be copied; the second and the third are auxiliary which are quantum counterparts of ‘blank paper’ and a ‘toner cartridge’ which are demanded by a classical copying machine.

Under real operating conditions, quantum cloning machines are affected by its decohering environment. The more complicated the system is the more likely the properties of some of components change. It is known how the UQCM works if one attempts to clone a state which is influenced by the thermal environment [9]. Here, we consider the complementary problem: How effective is the UQCM which is contaminated by thermal noise. We assume a natural setup when the auxiliary qubits are ‘dirty.’ We assume that before using them the qubits are in contact with thermal noise. It is pretty obvious that even a classical copying machine works worse if its toner cartridge is worn out or if one uses paper which is not ideally blank.

An effect of thermal contamination of qubits can be described using various methods [10] devoted to different problems. However, there are models applicable to a very broad class of situations. In this paper, we adopt Davies approach [11] which is both mathematically rigorous and physically consistent with microscopic description. It is also strictly Markovian what is probably its most bothersome feature since it cannot be used for systems driven by time-dependent external forces. Nevertheless, we claim that it is the best candidate for an ‘unbiased choice’ of decoherence.

The structure of the paper is the following: In Sect. 2, in order to keep this study self-contained, we briefly review UQCM considered here simply as a unitary transformation consisting of a net of gates [12]. In Sect. 3, the model of reduced dynamics of an open quantum system coupled to thermal Davies environment is formulated in terms of a quantum map [13]. In Sect. 4, there is a case study of how cloning machine contaminated by thermal noise copy states used in the six-state cryptography protocol [14]. Next, in Sect. 5 we discuss some main features of copying arbitrary input states with an emphasis given on an invariance an output fidelity with respect to certain parameters of the input. Finally, in Sect. 6 we summarize our work.

2 Universal quantum cloning machine: a brief review

An elementary and the most fundamental \(1\rightarrow 2\) universal cloning machine [3] is the unitary transformation

$$\begin{aligned} U_{\mathrm{clon}}:\mathbb {C}^2\otimes \mathbb {C}^2\otimes \mathbb {C}^2\rightarrow \mathbb {C}^2\otimes \mathbb {C}^2\otimes \mathbb {C}^2 \end{aligned}$$
(1)

which requires three input qubits: The first qubit \(Q_1\) is the one which an initial state is to be copied; the remaining two qubits \(Q_2\) and \(Q_3\) are auxiliary and represent ‘blank paper’ and a ‘toner cartridge’ inserted to the cloner. There is an implementation of universal cloner [3] via a quantum circuit [12]. The procedure of cloning consists of two (unitary) stages: preparation of the qubits \(Q_2\) and \(Q_3\) and copying the initial stage of the qubit \(Q_1\), namely

$$\begin{aligned} U_{\mathrm{clon}}=U_{\mathrm{cop}}U_{\mathrm{prep}} \end{aligned}$$
(2)

where

$$\begin{aligned} U_{\mathrm{prep}}= & {} R_2(\upsilon _3)CNOT_{32}R_3(\upsilon _2)CNOT_{23}R_2(\upsilon _1), \end{aligned}$$
(3)
$$\begin{aligned} U_{\mathrm{cop}}= & {} CNOT_{31} CNOT_{21} CNOT_{13} CNOT_{12}. \end{aligned}$$
(4)

For simplicity, we adopt the notation where \(R_i(\upsilon )\) denotes a tensor product of the i-th qubit rotation

$$\begin{aligned} R(\upsilon )=\left( \begin{array} {cc} \cos (\upsilon ) &{}\quad \sin (\upsilon ) \\ -\sin (\upsilon )&{}\quad \cos (\upsilon ) \end{array} \right) \end{aligned}$$
(5)

and the identity operator acting on remaining two qubits. Similarly, \(CNOT_{ij}\) acts as a gate of controlled negation with i the controlling and j the controlled qubits leaving the third k-th qubit untouched. For the rotation angles \(\upsilon _1=\upsilon _3=\pi /8\) and \(\upsilon _2=-\arcsin (1/2-\sqrt{3}/3)^{1/2}\), the cloning machine \(U_{\mathrm{clon}}\) is universal (UQCM) [3, 8]. In the paper, we assumes only these values for \(\upsilon _1, \upsilon _2\) and \(\upsilon _3\).

The action of cloning of a pure qubit state \(|\psi _{\mathrm{in}}\rangle \) is unitary and reads

$$\begin{aligned} \rho _{\mathrm{out}}=U_{\mathrm{clon}}\rho _{\mathrm{in}}U^\dagger _{\mathrm{clon}} \end{aligned}$$
(6)

where \(\rho _{\mathrm{in}}=|\psi _{\mathrm{in}}\rangle \langle \psi _{\mathrm{in}}|\otimes |0\rangle \langle 0| \otimes |0\rangle \langle 0|\). The initial state of the qubit \(Q_1\) is parameterized by two real numbers x and y, namely

$$\begin{aligned} |\psi _{\mathrm{in}}\rangle =|x,y\rangle := \cos (x)|0\rangle +\mathrm{e}^{iy}\sin (x)|1\rangle \end{aligned}$$
(7)

To quantify how successful is cloning, we consider, following Ref. [8], fidelity of the outputs,

$$\begin{aligned} F_2= & {} \text{ Tr }(\rho _{\mathrm{in}}\rho _2),\end{aligned}$$
(8)
$$\begin{aligned} F_3= & {} \text{ Tr }(\rho _{\mathrm{in}}\rho _3), \end{aligned}$$
(9)

where the reduced density operators of the qubit \(Q_2\) is \(\rho _2=\text{ Tr }_{1,3}[\rho _{\mathrm{out}}]\) and of the qubit \(Q_3\) is \(\rho _3=\text{ Tr }_{1,2}[\rho _{\mathrm{out}}]\), respectively. The cloning machine is universal if its output does not depend on the input state, i.e., neither on x nor on y which parameterize the state (7). It is symmetric if \(F_2=F_3\), and the best what can be achieved using UQCM is \(F_2=F_3=5/6\). We show that if the UQCM defined by Eqs. (2)–(3) is contaminated by thermal noise then it looses its universality and symmetry.

3 Model of thermal environment

A salient obstruction during the real cloning process is quantum decoherence which is caused by the influence of environment. In the following, we assume that the qubit \(Q_2\) or/and the qubit \(Q_3\) are affected by the environment while the copied qubit \(Q_1\) is ideally isolated from the environment. The influence of the environment on the qubit \(Q_i\) (\(i=2,\,3\)) is modeled by the Hamiltonian in the form:

$$\begin{aligned} H=H_i+H_{\mathrm{env}}+H_{\mathrm{int}} \end{aligned}$$
(10)

where \(H_i\) is the Hamiltonian of the qubit, \(H_{\mathrm{env}}\) models the environment and \(H_{\mathrm{int}}\) describes the qubit–environment interaction. For the qubit,

$$\begin{aligned} H_i=\frac{\omega _i}{2}(|1\rangle \langle 1|-|0\rangle \langle 0|), \end{aligned}$$
(11)

where \(\omega _i\) is the energy splitting of the i-th qubit (below we consider the case \(\omega _2=\omega _3=\omega \)). We assume that the interaction between the qubit and its environment satisfies the Davies weak coupling conditions [11] dedicated for rigorous construction of the qubit reduced (with respect to the environment) dynamics in terms of a completely positive (strictly Markovian) semigroup using parameters of the microscopic Hamiltonian of the full system [11]. As the Davies semigroups can be rigorously and consistently derived from microscopic models of open systems, they recover most of the desired thermodynamic and statistical–mechanical properties such as the detailed balance condition and the Gibbs canonical distribution in the stationary regime [11]. The Davies method has been successfully used in recent studies of various problems in quantum information and physics of open quantum systems including teleportation [15], entanglement dynamics [16], quantum discord [17, 18] or properties of geometric phases of qubits [19] and thermodynamic properties of nano-systems [20]. Here, instead of exploring the full power of the Davies semigroups, we consider only their certain elements: Davies maps [13]. The Davies map \(D=D(p,A,G,\omega ,t)\) acts as follows [13]:

$$\begin{aligned} D\bigg [|1\rangle \langle 1|\bigg ]= & {} [1-(1-p)(1-\mathrm{e}^{-At})]|1\rangle \langle 1|+(1-p)(1-\mathrm{e}^{-At})|0\rangle \langle 0| \end{aligned}$$
(12)
$$\begin{aligned} D\bigg [|1\rangle \langle 0|\bigg ]= & {} \mathrm{e}^{i\omega t -Gt}|1\rangle \langle 0| \end{aligned}$$
(13)
$$\begin{aligned} D\bigg [|0\rangle \langle 1|\bigg ]= & {} \mathrm{e}^{-i\omega t -Gt}|0\rangle \langle 1| \end{aligned}$$
(14)
$$\begin{aligned} D\bigg [|0\rangle \langle 0|\bigg ]= & {} p(1-\mathrm{e}^{-At})|1\rangle \langle 1|+[1-(1-\mathrm{e}^{-At})p]|0\rangle \langle 0|, \end{aligned}$$
(15)

where \(p\in [0,1/2]\) is related to the temperature T (here we set \(k_B=1\)) via:

$$\begin{aligned} p=\exp (-\omega /2T)/[\exp (-\omega /2T)+\exp (\omega /2T)]. \end{aligned}$$
(16)

The case \(T=0\) corresponds to the value \(p=0\) and for \(T\rightarrow \infty \) the parameter \(p\rightarrow 1/2\). The parameters \(A = 1/\tau _R\) and \(G = 1/\tau _D\), if interpreted in terms of spin relaxation dynamics [21], are related to the energy relaxation time \(\tau _R\) and the dephasing time \(\tau _D\), respectively [13]. The inequalities [21]

$$\begin{aligned} G \ge A/2 \ge 0 \end{aligned}$$
(17)

guarantee that the Davies map is a trace-preserving completely positive map. The limiting case \(A=0\) and \(G\ne 0\) corresponds to pure dephasing without dissipation of energy.

Finally, let us notice that in long-time limit the Davies map transforms any qubit state \(\rho \) into the equilibrium Gibbs state in the form:

$$\begin{aligned} \lim _{t\rightarrow \infty }D(p,A,G,\omega ,t)\rho =p|1\rangle \langle 1|+(1-p)|0\rangle \langle 0|. \end{aligned}$$
(18)

Now, we consider three distinct cases: the first when the cloning machine operator uses ‘dirty blank paper,’ the second when the ‘toner’ is noisy and the third when both resources are equally affected by thermal environment. Formally, this three cases correspond to three distinct input states:

$$\begin{aligned} \rho _{\mathrm{in}}^{\mathrm{I}}= & {} |\psi _{\mathrm{in}}\rangle \langle \psi _{\mathrm{in}}|\otimes D\bigg [|0\rangle \langle 0|\bigg ]\otimes |0\rangle \langle 0|\end{aligned}$$
(19)
$$\begin{aligned} \rho _{\mathrm{in}}^{\mathrm{II}}= & {} |\psi _{\mathrm{in}}\rangle \langle \psi _{\mathrm{in}}|\otimes |0\rangle \langle 0|\otimes D\bigg [|0\rangle \langle 0|\bigg ]\end{aligned}$$
(20)
$$\begin{aligned} \rho _{\mathrm{in}}^{\mathrm{III}}= & {} |\psi _{\mathrm{in}}\rangle \langle \psi _{\mathrm{in}}|\otimes D\bigg [|0\rangle \langle 0|\bigg ]\otimes D\bigg [|0\rangle \langle 0|\bigg ] \end{aligned}$$
(21)

Notice, that thermal contamination influences only the machine whereas the copied state \(|\psi _{\mathrm{in}}\rangle \) remains untouched. From Eqs. (12) to (15), it follows that in such a setting an output of the cloning machine is independent of G, i.e., on a dephasing.

4 Case study: six-state and BB84 protocols

Quantum cloning machines can be effectively utilized by Eve, an eavesdropper, who wants to know what Alice is saying to Bob. There are various methods which can be adopted by Eve, but all of them are limited by the laws of nature. Imperfect cloning is one of the tools which can be used to gain some knowledge about a subject of communication [6, 7]. Probably, the best-known application of quantum information processing is the quantum key distribution [6] when two parties (Alice and Bob) exchange secret key using quantum states as a resource. The first and still the most celebrated protocol is the famous BB84 [22] further modified into the six-state protocol [14]. In these protocols, Alice and Bob to communicate utilize the selected input states \(|\psi _{\mathrm{in}}\rangle =|x,y\rangle \) Eq. (7) forming the set of four BB84 states [22]

$$\begin{aligned} \text{ BB84 }=\big \{|\pi /4,0\rangle ,\,|\pi /4,\pi /2\rangle ,\,| \pi /4,\pi \rangle ,\,|\pi /4,3\pi /2\rangle \big \}. \end{aligned}$$
(22)

completed, in the case of six-state protocol, by two basis vectors [14]:

$$\begin{aligned} |0,0\rangle =|0\rangle ,\,\,\,|\pi /2,0\rangle =|1\rangle \end{aligned}$$
(23)

One of the possible attacks performed by Eve is based on a possibility of (imperfect) cloning of quantum states traveling from Alice to Bob [7, 23, 24]. There are two groups of strategies. The first is analyzed in the next section in more detail, when Eve performs her measurement on her copied raw qubit [23] before the sifting phase of the Alice–Bob communication. The second is discussed below, when Eve has an access to a quantum memory and can store her copied qubit and wait until she learn the basis used by Alice and Bob.

We consider the following attack strategy: Eve, using universal cloning machine, copies a qubit \(|\psi _{\mathrm{in}}\rangle =|x,y\rangle \) Eq. (7) sent by Alice to Bob; i.e., she performs the \(U_{\mathrm{clon}}\) Eq. (6). The output is a three-qubit state \(\rho _{\mathrm{out}}\). Eve sends a single qubit \(\rho _2=\text{ Tr }_{1,3}[\rho _{\mathrm{out}}]\) to Bob and keeps \(\rho _3=\text{ Tr }_{1,2}[\rho _{\mathrm{out}}]\) for a further analysis. In this paper, we assume that in addition to the fundamental limitation for copying originating from the no-cloning theorem the cloning procedure is contaminated by thermal noise; i.e., instead of the input state \(|\psi _{\mathrm{in}}\rangle \otimes |0\rangle \otimes |0\rangle \) the Eve’s copying machine works with one among the states Eq. (19) depending of the character of the contamination. The thermal noise, given here by the Davies map \(D[\cdot ]\), essentially affects both the states which arrives to Bob and information gained by Eve. We qualify [8] the effect of cloning by its fidelities given in Eq. (8): \(F_{\mathrm{Bob}}=F_2\) in the case of Bob and \(F_{\mathrm{Eve}}=F_3\) in the case of Eve. The relation between them quantifies security of the key distribution protocol [7, 8]. In particular, for the BB84 protocol [7, 24, 25] the secret key can no longer be extracted as soon as \(F_2=F_3\) [7]. For the BB84 and the six-state protocols, the cloning contaminated by thermal noise is given by the unitary transformation \(U_{\mathrm{clon}}\rho _{\mathrm{in}}^{i}U^\dagger _{\mathrm{clon}}\) (with \(i=\)I, II, III) performed by Eve for the input states in Eq. (19) with \(|\psi _{\mathrm{in}}\rangle \) given in Eqs. (22) and (23). Partial trace with respect to the first qubit followed by the partial trace with respect to either the third or the second qubit allows to calculate the state of the Bob’s and Eve’s qubit, respectively.

For three different input states \(\rho _{\mathrm{in}}^{\mathrm{I,II,III}}\) depending on the type of thermal contamination, there are only three possible values of the output fidelities \(F_2\) (Bob) and \(F_3\) (Eve), namely

$$\begin{aligned} F_{2,3}=\{5/6, F_{A}, F_B\}, \end{aligned}$$
(24)

where

$$\begin{aligned} F_A= \frac{1}{6}+\frac{2}{3}p+\frac{2}{3}{\mathrm{e}^{-At}} \left( 1-\frac{2}{3}p\right) \end{aligned}$$
(25)

and

$$\begin{aligned} F_B= & {} \frac{5}{6}-\frac{4}{3}p+\frac{4}{3}p^{2}+{\mathrm{e}^{-At}}\left( 4p-\frac{4}{3}-\frac{8}{3}p^2 \right) \nonumber \\&+\,\frac{4}{3}{\mathrm{e}^{-2At}}\left( 1-2p+p^2 \right) \end{aligned}$$
(26)

Here and in further discussion, we set \(\omega =1\) and work in rescaled time units \(t\rightarrow t/\omega \). The possible outcomes for different inputs are summarized in Table 1. It follows that a particular value of the output fidelity depends on the input \(\rho _{\mathrm{in}}^{\mathrm{I,II,III}}\) defined in Eqs. (19)–(21). Let us notice that some of the BB84 states can be cloned with the output fidelity \(F_{2,3}=5/6\), i.e., as good as in the case of noiseless cloning machine. The exception is the input \(\rho _{\mathrm{in}}^{\mathrm{III}}\) for which \(F_{2,3}\,<\,5/6\) at nonzero temperature \(T\,>\,0\). If one considers the noisy cloning machine as a probabilistic device, it can operate as good as a noiseless one (but with probability 1/3) on a set of six states in Eqs. (23) and (22). Moreover, let us notice for \(\rho _{\mathrm{in}}^{\mathrm{I,II}}\) cloning fidelity is never worse than \(F_A\).

Table 1 Output fidelity \(F_2\) and \(F_3\) defined in Eqs. (8) and (9) for the noisy input state \(\rho _{\mathrm{in}}^{\mathrm{I}}\) in (a); for \(\rho _{\mathrm{in}}^{\mathrm{II}}\) in (b) and for \(\rho _{\mathrm{in}}^{\mathrm{III}}\) in (c)
Full size table

There is a qualitative difference between the output fidelity \(F_{A}=F_A(t)\) in Eq. (25) and \(F_B=F_B(t)\) in Eq. (26) considered as a function of time. For any fixed value of temperature p, the function \(F_A(t)\) exhibits a strictly exponential decay whereas \(F_B(t)\) is nonmonotonic with respect to change of t, cf. panels (a) and (b) in Fig. 1. In particular, for \(p=0\) the output fidelity \(F_B(t)\) first decreases reaching its minimal value, and next it increases to the value 5/6. In panels (c) and (d) of Fig. 1, the influence of the energy relaxation rate A is depicted at zero temperature, \(p=0\). We detect that the fidelity \(F_B(t)\) decays to a minimum at the characteristic time \(t_c\) and next it increases to the asymptotic value 5/6. The value of \(t_c\) depends on the relaxation rate A: If A is larger, then \(t_c\) is smaller.

Fig. 1
figure 1

Output fidelity \(F=F_A\) (a) and \(F=F_B\) (b) calculated for \(A=1\) and different values of p. Output fidelity \(F=F_A\) (c) and \(F=F_B\) (d) calculated for \(p=0\) and different values of A. e Long-time limit \(F=\lim _{t\rightarrow \infty }F_A\) and \(F=\lim _{t\rightarrow \infty }F_B\) versus the effective temperature p (Color figure online)

Full size image

The qualitative difference between \(F_A\) and \(F_B\) is even more apparent in the long-time limit. It follows form Eqs. (25) and (26) that the long-time limit is obviously A-independent:

$$\begin{aligned} \lim _{t\rightarrow \infty } F_A= & {} \frac{1}{6}+\frac{2}{3}p\end{aligned}$$
(27)
$$\begin{aligned} \lim _{t\rightarrow \infty } F_B= & {} \frac{5}{6}-\frac{4}{3}p\left( p-1\right) \end{aligned}$$
(28)

In panel (e) of Fig. 1, we plot these limits as a function of temperature p. For infinite temperature, \(p=1/2\) both \(F_{A,B}\rightarrow 1/2\). For finite temperatures, \(p\,<\,1/2\), the functions \(F_A\) and \(F_B\) are significantly different from the worst value 1/2. The conclusion is apparent: Even in the long-time limit, the cloning machine contaminated by thermal noise can be still better than pure guess.

Properties of fidelities summarized in Table 1 need to be taken into account in security analysis of the BB84 quantum key distribution protocol with respect to the attack of an eavesdropper equipped with cloning machine and quantum memory, i.e., the one who gains information of the copied qubit after the sifting phase of Alice–Bob communication. Let us focus on the most contaminated case (Table 1(c)). Security condition \(F_{\mathrm{Eve}}<F_{\mathrm{Bob}}\) (i.e., \(F_3\,<\,F_2\)) holds provided that \(F_B\,<\,F_A\). In particular, the deep minimum of \(F_B\) presented in panel (c) of Fig. (1) can be utilized: If Bob and Alice are able to finalize their total communication before \(F_B\) increases, they can essentially get the better of Eve.

Let us notice that the reasoning presented above is based on the assumption that Eve knows if she has either \(\rho _2\) or \(\rho _3\) at her disposal. Her potential ignorance of that aspect of copying procedure introduces additional randomness and decreases her information.

5 General input states

In this paper, we consider the cloning machine which in its noiseless limit is universal. Hence, it is natural not to restrict our attention to a useful but narrow class of cloned states Eqs. (23) and (22) but rather attempt to analyze an effect of thermal contamination for the cloning general state \(|x,y\rangle \) given in Eq. (7). In this section, we briefly discuss this question.

In calculations, we have used analytic results for the output fidelity \(F_{2,3}\), but they are rather complicated and their presentation in a clear and compact form, as we did in the previous section, is a formidable task. In order to reduce the complexity of the problem, we limit our consideration to a long-time regime and study \(\lim _{t\rightarrow \infty } F_{2,3}\). Yet, the results exhibit some peculiar features and symmetries. First, as one could expect neither \(F_2\) nor \(F_3\) depends on A in the long-time limit. Second, there are two types of y-dependence of the output fidelity. They can be either y-periodic or y-independent. If the input is \(\rho _{\mathrm{in}}^I\) or \(\rho _{\mathrm{in}}^{\mathrm{III}}\), i.e., the auxiliary qubit labeled by 2 is contaminated by thermal noise, then \(\lim _{t\rightarrow \infty } F_{3}\) and \(\lim _{t\rightarrow \infty } F_{2}\) are y-independent. In other words, the cloning machine not universal any more works as a phase-invariant cloner. In all the remaining cases, the output fidelities are periodic functions of y. Moreover, if the output is y-dependent, we assume y to be fixed. We chose y which is by no means specific and analyze the qualitative features of x-dependence for different values of p. In panel (a) of Fig. 2, we present \(\lim _{t\rightarrow \infty } F_{2}\) for \(\rho _{\mathrm{in}}^{\mathrm{II}}\). There is a symmetry \(\lim _{t\rightarrow \infty } F_{2}=\lim _{t\rightarrow \infty } F_{3}\) of output fidelities for the inputs \(\rho _{\mathrm{in}}^{\mathrm{I}}\) and \(\rho _{\mathrm{in}}^{\mathrm{II}}\) as it is presented in panel (b) and (c) of Fig. 2. Let us observe that even for \(p=1/2\) the output fidelity \(\lim _{t\rightarrow \infty } F_{2,3}\ne 1/2\) except only for very special values of x as it is indicated in panel (a)–(c). It means that regardless of the temperature the cloning machine works. Let us notice that it is no more the case if both auxiliary qubits are contaminated by thermal noise. In panel (d) and (e) of Fig. 2, we present \(\lim _{t\rightarrow \infty } F_{2,3}\) for \(\rho _{\mathrm{in}}^{\mathrm{III}}\) when both the auxiliary qubits are noisy. Two noisy auxiliary qubits result is lowering an amplitude of an output fidelity. Let us also notice that for \(p=1/2\,\lim _{t\rightarrow \infty } F_{2,3}=1/2\) for all values of x, and hence the cloning machine becomes useless since it is no more effective than a random guess.

Fig. 2
figure 2

a Output fidelity \(F=\lim _{t\rightarrow \infty }F_2\) for different initial states \(|x,\pi /3\rangle \) in Eq. (7) for initial preparation \(\rho _{\mathrm{in}}^{\mathrm{II}}\) Eq. (20). b Output fidelity \(F=\lim _{t\rightarrow \infty }F_3\) [\(F=\lim _{t\rightarrow \infty }F_2\)] for different initial states \(|x,\pi /3\rangle \) in Eq. (7) for initial preparation \(\rho _{\mathrm{in}}^{\mathrm{II}}\) Eq. (20) [resp. \(\rho _{\mathrm{in}}^{\mathrm{I}}\) Eq. (19)]. c Output fidelity \(F=\lim _{t\rightarrow \infty }F_3\) for different initial states \(|x,y\rangle \) in Eq. (7) for initial preparation \(\rho _{\mathrm{in}}^{\mathrm{I}}\) Eq. (19). d Output fidelity \(F= \lim _{t\rightarrow \infty }F_2\) for different initial states \(|x,y\rangle \) in Eq. (7) for initial preparation \(\rho _{\mathrm{in}}^{\mathrm{III}}\) Eq. (21). e Output fidelity \(\lim _{t\rightarrow \infty }F_3\) for different initial states \(|x,\pi /3\rangle \) in Eq. (7) for initial preparation \(\rho _{\mathrm{in}}^{\mathrm{III}}\). The results in panels (c) and (d) are y-independent (Color figure online)

Full size image

Let us consider, following Refs. [23, 24, 26], a particular case of an attack of an eavesdropper Eve performed on a raw qubit traveling from Alice to Bob before the sifting stage of the communication. We assume that Eve is able to clone the qubit using the universal cloning machine \(\rho _{\mathrm{out}}=U_{\mathrm{clon}}\rho _{\mathrm{in}}^{\mathrm{III}}U^\dagger _{\mathrm{clon}}\) but then, contrary to the case discussed in previous section, she cannot wait until the sifting phase but she measures her copy \(\rho _3=\text{ Tr }_{1,3}[\rho _{\mathrm{out}}]\) in a randomly guessed basis which includes a state \(|\zeta \rangle = \cos (\zeta /2)|0\rangle +\sin (\zeta /2)|1\rangle \) paramterized by a variable angle \(\zeta \). Fidelity of her guess is given by:

$$\begin{aligned} F(\zeta )= \langle \zeta |\rho _{3}|\zeta \rangle \end{aligned}$$
(29)

Let us focus on the BB84 protocol when Alice sends one among four states \(|\pi /4,y\rangle \) with \(y=0,\pi /4,\pi /2,\pi ,3\pi /2\) Eq. (22). For \(y=\pi /2\) and \(y=3\pi /2\), the corresponding fidelity depends neither on \(\zeta \) nor on any of the parameters of the environment and reads \(F(\zeta )=1/2\). For the remaining states with \(y=0\) and \(y=\pi \), the fidelity is given by:

$$\begin{aligned} F(\zeta ,y)= & {} \frac{1}{2}+\frac{\sqrt{2}}{6}(1+\mathrm{e}^{-At}) \left[ \sin \left( \frac{1}{4}\pi +\zeta \right) -\cos \left( \frac{1}{4}\pi +\zeta \right) \right] \nonumber \\&+\,\frac{\sqrt{2}}{6}p(1-\mathrm{e}^{-At}) \left[ \sin \left( \frac{1}{4}\pi +\zeta \right) +\cos \left( \frac{1}{4}\pi +\zeta \right) \right] \end{aligned}$$
(30)

Let us notice that as the above formula does not depend on \(G=1/\tau _D\), the quality of Eve’s choice of the measurement basis is not affected by dephasing time of the qubit.

6 Summary

Power of quantum cloning machines as an answer for the celebrated no-cloning theorem [1] suffers from various drawbacks and limitations. In our work, we have studied a simplest and probably most obvious problem—thermal noise affecting auxiliary qubits necessary for implementing [12] the UQCM. We adopt the Davies maps [13] originating from the most general Markovian treatment of open quantum systems. In our studies, which are complementary to the earlier analysis of cloning thermally modified quantum states [9], we have shown certain undesirable, while expected, deterioration of an effectiveness of cloning. Nevertheless, in most cases the cloning machine works also in the presence of thermal noise contaminating its auxiliary qubits. First and the most general conclusion is that for the Davies Markovian approximation the output of the cloning machine never depends on the dephasing time \(\tau _D=1/G\) of auxiliary qubits no matter what the state is to be cloned.

We have presented a detailed analysis for cloning of quantum states applicable in the well-known six-state crypto-protocol [14]. We show that there are only three different values of the output fidelity quantifying effectiveness of cloning. One of them is the same as for a ‘perfect’ cloning of noiseless machine, i.e., 5/6. The other two exhibit qualitatively different properties controllable by temperature p of the environment.

As we start with the universal cloner, we also discuss more general classes of initial states. In the presence of thermal contamination, the cloning machine loses its universality but still it can work identically on certain subclasses of states. Interesting observation is that under certain circumstances one of its output is phase invariant. Unfortunately, a choice of the proper output qubit is to be done randomly. Nevertheless, in many cases even for high temperature of the environment influencing auxiliary qubits, the cloning process is more effective than pure guessing (\(F\ne 1/2\)).

Typical problems raising time and again in every nine-to-five job are often linked to a faulty copying machines. Technical staff responsible for an office equipment knows very well how to recognize and fix such problems. We hope that our work may be useful for technicians maintaining quantum copying machines. If not today, hopefully in a not very far future.