1 Introduction

A unique phenomenon, entanglement, plays an important role in the field of quantum computation and quantum information processing [1–7]. Due to its important properties, the quantum entanglement has broad practical applications. For example, the powerful speedup of quantum computation resorts to multi-qubit entanglement [1]. What is more, in quantum communication, the multi-qubit entangled states can be used as quantum channel in some typical long-distance quantum communication proposals, such as quantum key distribution (QKD) [2], quantum teleportation [3], quantum dense coding [4, 5], quantum secret sharing [6, 7]. We all know that most of the above protocols can be realized ideally with one perfect probability and unit fidelity require that two or more distant parties share maximally entangled states. Generally speaking, the entangled states are first produced locally and distributed to different distant locations. Theoretically, one can assume, nevertheless, that the quantum channel used to share the quantum entangled states is noiseless. However, in a practical transmission or the process for storing an entangled quantum system, the entanglement is inevitably influenced by channel noises and imperfect sources. That is, when qubits are coupled to the environment, the fragile superpositions of quantum states are easily destroyed and the advantage of quantum information methods is reduced. And, decoherence will degrade the maximally entanglement into a pure less-entangled state or even make the entanglement into a mixed state and cause the error probability scales exponentially with the length of channel. Polluted entanglement is always responsible for failing in quantum dense coding, reducing the fidelity of quantum teleportation and insecurity of the key of quantum cryptography.

In order to reduce the impact of environmental noises and improve the fidelity and security of the quantum communication scheme, several strategies have been devised to deal with decoherence and each of them is appropriate for a specific type of coupling with the environment. (1) If the interaction of the qubits and the environment is weak enough, such that qubits are affected only with a very low probability, a good strategy [8] would be to add redundancy when encoding the quantum information in order to detect and correct the errors by active quantum error correcting code. (2) The second approach [9] employs dynamical decoupling, where rapid switching is used to average out the effects of a relatively slowly decohering environment. (3) One can exploit entanglement concentration or entanglement purification to improve the entanglement of the quantum system if the destructive effect of the noises are not severe. Generally speaking, entanglement purification is used to distill the nonlocal maximally entangled states from the system of mixed states [10–22], while the process of entanglement concentration is distilling the less-entangled pure states to obtain the nonlocal maximally entangled states. Compared with entanglement purification, entanglement concentration is more efficient for the remote parties in quantum communication, because entanglement concentration can obtain a maximally entangled state directly. In 1996, the first entanglement concentration protocol (ECP) proposed by Bennett et al. [23] for two-photon systems by using the Schmidt projection method and collective measurement. Since this pathbreaking work, an increasing number of interesting ECPs [24–32] have been proposed. For example, Bose et al. [24] proposed an ECP based on entanglement swapping in 1999. Yamamoto et al. [28] presented an experimental scheme for concentrating entanglement from partially entangled photon pairs by local operations and classical communication in 2001. In the years that followed, Sheng et al. put a series of ECPs [29–31] forward resort to some interesting means. It is worth to note that in 2008, Sheng et al. [29] proposed an ECP for reconstructing some maximally entangled multipartite states from partially entangled ones by exploiting cross-Kerr nonlinearities to distinguish the parity of two polarization photons. Two years later, Sheng et al. [30] presented the first ECP assisted with single photons based on cross-Kerr nonlinearity. In 2012, they also proposed two two-step practical ECPs [32] for concentrating an arbitrary three- particle less-entangled \(W\) state into a maximally entangled \(W\) state assisted with single photons. Since then, different ECPs [27, 31] assisted with single photons and cross-Kerr nonlinearity have been put forward successively.

So far, most of ECPs just deal with the concentration of Bell states, Greenberger–Horne–Zeilinger (GHZ) states, and W states [23–32]. Only few ECPs for concentrating cluster states [33]. As far as we know, the cluster states have both the properties of Bell states and W states and are harder to be destroyed by local operations than Bell states [34]. So the research on the concentration of cluster states is useful and necessary [35]. In 2013, Binayak et al. [33] developed an ECP for a special less-entangled pure cluster state with an even number of qubits, and they used only local operations for this protocol. However, the success probability of this ECP is not high.

In this paper, we propose an ECP for pure partially entangled cluster states with the weak cross-Kerr nonlinearity. With two single photons and one less-entangled cluster state, we can perform this task. Additionally, the quantum-nondemolition detector (QND) constructed with weak cross-Kerr nonlinearity is adopted in the protocol; therefore, the sophisticated single-photon detectors are not required. We should note that a higher success probability can be obtained than that in Ref. [33], since the discarded items in the protocol can be reused for further concentration. And furthermore, in principle, our entanglement concentration of less-entangled cluster states can be extended to concentrate the \(4N\)-qubit cluster states. These advantages make the protocol more feasible in practical applications.

This paper is organized as follows. In Sect. 2, we explain the basic principle of the present ECP with weak cross-Kerr nonlinearity. We show that a less-entangled cluster state can be concentrated with a certain success probability by iterating the entanglement concentration process several times. In Sect. 3, we extend this protocol to concentrate the system of the less-entangled \(4N\)-qubit cluster states. In Sect. 4, we make a discussion and summary.

2 Entanglement concentration of less-entangled cluster states

At the beginning of the detailed discussion, let us first introduce the cross-Kerr nonlinearity, which is a powerful tool for constructing QND and has the potential availability of being able to condition the evolution of our system without necessarily destroying the single photons. The Hamiltonian of the cross-Kerr nonlinearity is \(H_{\mathrm{QND}}=\hbar \chi {\hat{a}_s}^+\hat{a}_s{\hat{a}_p}^+\hat{a}_p\), where \({\hat{a}_p}^+\) (\(\hat{a}_p\)) is the creation operator (annihilation operator) of the probe mode and \({\hat{a}_s}^+\) (\(\hat{a}_s\)) is the creation operator (annihilation operator) of the signal mode. \(\chi \) is the coupling strength of the Kerr medium, which is decided by the property of nonlinear material. If we consider a single-photon state \(|\phi \rangle =\alpha |0\rangle +\beta |1\rangle \), where \(|0\rangle \) (\(|1\rangle \)) denotes the no photons (one single photon), then probe mode is a coherent state \(|\alpha \rangle \). After the interaction with the weak cross-Kerr nonlinear medium, the whole system evolves as

$$\begin{aligned} U_\mathrm{CK}|\phi \rangle |\alpha \rangle = e^{iH_{\mathrm{QND}}t/\hbar }(\alpha |0\rangle +\beta |1\rangle )|\alpha \rangle = \alpha |0\rangle |\alpha \rangle +\beta |1\rangle |\alpha e^{i\theta }\rangle , \end{aligned}$$
(1)

here \(\theta =\chi t\) and \(t\) is the interaction time. We can observe that the photon state \(|\phi \rangle \) is unaffected by the interaction. Surprisingly, the coherent state picks up a phase shift of \(\theta \) directly proportional to the number of the photons in the Fock state \(|\phi \rangle \), which can be read out with a general homodyne–heterodyne measurement. This is the main principle of the cross-Kerr nonlinearity, and the good feature can be used to construct a QND device. One can exactly check the number of photons in the Fock state but not destroy them. In fact, the cross-Kerr nonlinearity has been widely studied in construction of controlled-NOT gates [36], performing entanglement purification protocols [15–17, 37, 38], performing ECPs [29, 30], completing Bell-state analysis [39], and performing other quantum communication and computation [40–53].

Now, we will introduce the basic principle of our ECP for partially entangled cluster states with weak cross-Kerr nonlinearity. We first suppose a less-entangled four-photon cluster state is initially in

$$\begin{aligned} |\phi _{ABCD}\rangle= & {} a|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D+\frac{ac}{b}|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D\nonumber \\&+\,b|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D-c|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D, \end{aligned}$$
(2)

with \(|a|^2+|ac/b|^2+|b|^2+|c|^2=1\). The subscripts \(A\), \(B\), \(C\), and \(D\) represent the photons belongs to Alice, Bob, Charlie, and Dick, respectively. The present ECP could be completed in two steps. The first step is operated by Dick, and the second one is operated by Bob. The other parties only need to retain or discard their photon according to the measurement results from Bob and Dick by classical communications.

Fig. 1
figure 1

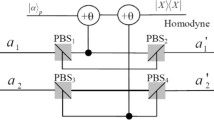
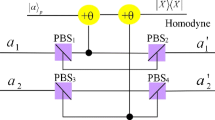
Schematic drawing of our ECP with the weak cross-Kerr nonlinearity. QNDs \((s=1,2)\) is described in Fig. 2. PBSs \((s=1,2)\) transmits the horizontal polarization and reflect the vertical polarization. \(\hbox {HWP}_{45}\) can rotate the polarization of the state by \(45^\circ \). \(D_1\), \(D_2\), \(D_3\), and \(D_4\) are four single-photon conventional photon detectors

Full size image
Fig. 2
figure 2

Schematic diagram of the nondestructive quantum-nondemolition detector (QND). This QND is used to distinguish horizontal \(|HH\rangle \) and \(|VV\rangle \) form \(|HV\rangle \) and \(|VH\rangle \). Here, \(H\) and \(V\) represent horizontal polarization and vertical polarization, respectively. Each polarization beam splitter (PBS) is used to pass through \(H\) polarization photons and reflect \(V\) polarization photons. The action of the weak cross-Kerr nonlinearity puts a phase shift \(\theta \) or a phase shift \(-\theta \) on the coherent probe beam if there is a photon in mode couple. After the nonlinear interactions, the probe beam picks up the phase shift \(\theta \) or \(-\theta \) if the state is \(|HV\rangle \) or \(|VH\rangle \), respectively. Otherwise, if the state is \(|HH\rangle \) or \(|VV\rangle \), the probe beam picks up no phase shifts

Full size image

The principle of the present entanglement concentration is shown in Fig. 1. For the first step of our protocol, Dick prepares an ancillary single photon \(E\) emitting from \(S_1\) which in the state as

$$\begin{aligned} |\varphi \rangle _E=\frac{1}{\sqrt{a^2+b^2}}(b|H\rangle _E+a|V\rangle _E). \end{aligned}$$
(3)

After the photon \(D\) and photon \(E\) passes through the \(\hbox {QND}_1\) as shown in Fig. 2, the whole system of the single photon \(E\) and the \(|\phi _{ABCD}\rangle \) combined with the coherent state \(|\alpha \rangle \) can be written as

$$\begin{aligned} |\Psi _{ABCDE}\rangle= & {} \frac{1}{\sqrt{a^2+b^2}}(ab|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D|H\rangle _E|\alpha \rangle \nonumber \\&+\,a^2|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D|V\rangle _E|\alpha e^{i\theta }\rangle \nonumber \\&+\,ac|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D|H\rangle _E|\alpha \rangle \nonumber \\&+\,\frac{a^2c}{b}|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D|V\rangle _E|\alpha e^{i\theta } \rangle \nonumber \\&+\,b^2|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D|H\rangle _E|\alpha e^{-i\theta } \rangle \nonumber \\&+\,ab|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D|V\rangle _E|\alpha \rangle \nonumber \\&-\,bc|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D|H\rangle _E|\alpha e^{-i\theta }\rangle \nonumber \\&-\,ac|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D|V\rangle _E|\alpha \rangle ). \end{aligned}$$
(4)

If we choose an X-quadrature measurement on the coherent state \(|\alpha \rangle \), we can distinguish the outcomes in two classes with different phase shifts \(\pm \theta \) and 0. That is, (1) if the coherent state \(|\alpha \rangle \) picks up no phase shift, we can confirm that the system of the single photon \(E\) and the \(|\phi _{ABCD}\rangle \) in the state

$$\begin{aligned} |\Psi '_{ABCDE}\rangle _1= & {} \frac{1}{\sqrt{ a^2+b^2}}(ab|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D|H\rangle _E\nonumber \\&+\,ac|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D|H\rangle _E\nonumber \\&+\,ab|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D|V\rangle _E-ac|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D|V\rangle _E).\nonumber \\ \end{aligned}$$
(5)

(2) If the coherent state \(|\alpha \rangle \) picks up the phase shift \(\pm \theta \) (The homodyne measurement cannot distinguish the \(\pm \theta \) [36]), we can confirm that the system of the single photon \(E\) and the \(|\phi _{ABCD}\rangle \) in the state

$$\begin{aligned} |\Psi '_{ABCDE}\rangle _2=&\frac{1}{\sqrt{a^2+b^2}}(a^2|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D|V\rangle _E\nonumber \\&+\,\frac{a^2c}{b}|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D|V\rangle _E\nonumber \\&+\,b^2|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D|H\rangle _E-bc|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D|H\rangle _E).\nonumber \\ \end{aligned}$$
(6)

Here, we first consider the system of the single photon \(E\) and the \(|\phi _{ABCD}\rangle \) in the state in Eq. (5). Dick performs a \(45^\circ \) polarization measurement on the photon \(E\) with \(1/4\)-wave plate (\(\hbox {HWP}_{45}\)) which is described as

$$\begin{aligned}&|H\rangle _E\rightarrow \frac{1}{\sqrt{2}}(|H\rangle _E+|V\rangle _E),\nonumber \\&|V\rangle _E\rightarrow \frac{1}{\sqrt{2}}(|H\rangle _E-|V\rangle _E). \end{aligned}$$
(7)

After the above rotation operation, \(|\Psi '_{ABCDE}\rangle _1\) becomes

$$\begin{aligned} |\Psi ''_{ABCDE}\rangle= & {} \frac{1}{\sqrt{2(a^2+b^2)}} [(ab|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D+ac|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D\nonumber \\&+\,ab|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D-ac|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D)|H\rangle _E\nonumber \\&+\,(ab|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D+ac|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D\nonumber \\&-\,ab|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D+ac|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D)|V\rangle _E]. \end{aligned}$$
(8)

Then, the single photon \(E\) will meet polarization beam splitter 1 (\(\hbox {PBS}_1\)), which always transmits \(H\) polarizing photons and reflects \(V\) polarizing photons (all PBSs in this paper work in this way). At last, the outcomes are detected by two conventional photon detectors \(D_1\) and \(D_2\). The conventional photon detectors \(D_1\) and \(D_2\) can only distinguish between the presence and absence of photons, and need not distinguish a single photon from two or more photons resulting in that no information on the exact number of the photons can be obtained. If the detector \(D_1\) fires, the four photons \(ABCD\) in the state are

$$\begin{aligned} |\Psi ''_{ABCD}\rangle _1= & {} \frac{1}{\sqrt{2({a_1}^2+{b_1}^2)}}(a_1|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D+b_1|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D\nonumber \\&+\,a_1|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D-b_1|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D), \end{aligned}$$
(9)

with \(a_1=ab\), \(b_1=ac\). Otherwise, if the detector \(D_2\) fires, the four photons \(ABCD\) in the state are

$$\begin{aligned} |\Psi ''_{ABCD}\rangle _2= & {} \frac{1}{\sqrt{2({a_1}^2+{b_1}^2)}}(a_1|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D+b_1|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D\nonumber \\&-\,a_1|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D+b_1|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D), \end{aligned}$$
(10)

with \(a_1=ab\), \(b_1=ac\). Dick can transform the state \(|\Psi ''_{ABCD}\rangle _2\) into the state \(|\Psi ''_{ABCD}\rangle _1\) with a phase-flip operation \(\sigma _z=|H\rangle \langle H|-|V\rangle \langle V|\) on his photon \(D\). The success probability of getting the state \(|\Psi ''_{ABCD}\rangle _1\) in Eq. (9) is \({P_0}^1=\frac{2a^2(b^2+c^2)}{a^2+b^2}\), where, the superscript 1 means the first concentration step, and the subscript 0 is the iteration number. The state in Eq. (9) can be used to realize the ECP in second concentration step.

The discarded state in Eq. (6) can also be reused to generate the less-entangled four-photon state in Eq. (9) with different parameters. After normalizing, Eq. (6) changes into

$$\begin{aligned} |\varphi _{ABCD}\rangle _1= & {} \frac{b}{\sqrt{(a^4+b^4)(b^2+c^2)}}\Big (a^2|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D\nonumber \\&+\,\frac{a^2c}{b}|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D\nonumber \\&+\,b^2|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D-bc|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D\Big ). \end{aligned}$$
(11)

Compared with Eq. (2), it is not difficult to find that Eq. (11) has the same form as Eq. (2) but with different parameters. We need only to replace the parameters \(a\), \(ac/b\), \(b\) and \(c\) in Eq. (2) with the parameters \(a'=a^2\), \(a'c'/b'=a^2c/b\), \(b'=b^2\) and \(c'=bc\), respectively. As a result, the state in Eq. (11) can be reconcentrated in the next round. For example, Dick prepares an another ancillary single photon \(E_1\) in the state \(|\varphi \rangle _{E_1}=\frac{1}{\sqrt{{a'}^2+{b'}^2}}(b'|H\rangle +a'|V\rangle )_{E_1}\) and sends photons \(E_1\) and \(D\) pass through \(\hbox {QND}_1\) again,

$$\begin{aligned} |\varphi _{ABCDE_1}\rangle _1&\xrightarrow []{\mathrm{QND}_1}\frac{b'}{\sqrt{(a'^2+b'^2)^2(b'^2+c'^2)}}(a'b'|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D|H\rangle _{E_1}|\alpha \rangle \nonumber \\&+\,a'^2|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D|V\rangle _{E_1}|\alpha e^{i\theta }\rangle \nonumber \\&+\,a'c'|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D|H\rangle _{E_1}|\alpha \rangle \nonumber \\&+\,\frac{a'^2c'}{b'}|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D|V\rangle _{E_1}|\alpha e^{i\theta }\rangle \nonumber \\&+\,b'^2|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D|H\rangle _{E_1}|\alpha e^{-i\theta }\rangle \nonumber \\&+\,a'b'|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D|V\rangle _{E_1}|\alpha \rangle \nonumber \\&-\,b'c'|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D|H\rangle _{E_1}|\alpha e^{-i\theta }\rangle \nonumber \\&-\,a'c'|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D|V\rangle _{E_1}|\alpha \rangle ). \end{aligned}$$
(12)

We choose an X-quadrature measurement on the coherent state \(|\alpha \rangle \), if \(|\alpha \rangle \) picks up no phase shift,

$$\begin{aligned} |\varphi '_{ABCDE_1}\rangle _1= & {} \frac{b'}{\sqrt{(a'^2+b'^2)^2(b'^2+c'^2)}}(a'b'|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D|H\rangle _{E_1}\nonumber \\&+\,a'c'|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D|H\rangle _{E_1}+a'b'|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D|V\rangle _{E_1}\nonumber \\&-\,a'c'|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D|V\rangle _{E_1}). \end{aligned}$$
(13)

If \(|\alpha \rangle \) picks up the phase shift \(\pm \theta \),

$$\begin{aligned} |\varphi '_{ABCDE_1}\rangle _2= & {} \frac{b'}{\sqrt{(a'^2+b'^2)^2(b'^2+c'^2)}}\Big (a'^2|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D|V\rangle _{E_1}\nonumber \\&+\,\frac{a'^2c'}{b'}|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D|V\rangle _{E_1}+b'^2|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D|H\rangle _{E_1}\nonumber \\&-\,b'c'|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D|H\rangle _{E_1}\Big ). \end{aligned}$$
(14)

For Eq. (13), Dick sends the photons \(E_1\) passing through \(\hbox {HWP}_{45}\) as shown in Fig. 2 again. The state in Eq. (13) evolves as

$$\begin{aligned} |\varphi '_{ABCDE_1}\rangle _1&\xrightarrow []{\mathrm{HWP}_{45}}\frac{b'}{\sqrt{2(a'^2+b'^2)^2(b'^2+c'^2)}} [(a'b'|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D\nonumber \\&+\,a'c'|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D+a'b'|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D\nonumber \\&-\,a'c'|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D)|H\rangle _{E_1}+(a'b'|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D\nonumber \\&+\,a'c'|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D-a'b'|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D\nonumber \\&+\,a'c'|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D)|V\rangle _{E_1}]. \end{aligned}$$
(15)

Finally, photon \(E_1\) will be detected by photon detectors \(D_1\) and \(D_2\). If the detector \(D_1\) fires, the four photons \(ABCD\) in the state

$$\begin{aligned} |\varphi '_{ABCD}\rangle '_1 \!= & {} \!\frac{1}{\sqrt{2\left[ {(a^1_1)}^2+{(b^1_1)}^2\right] }}\Big (a^1_1|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D\!+\!b^1_1|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D \nonumber \\&+\,a^1_1|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D-b^1_1|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D\Big ), \end{aligned}$$
(16)

with \(a^1_1=a'b'\), \(b^1_1=a'c'\). Otherwise, if the detector \(D_2\) fires, the four photons \(ABCD\) in the state

$$\begin{aligned} |\varphi '_{ABCD}\rangle '_2 \!= & {} \!\frac{1}{\sqrt{2\left[ {(a^1_1)}^2+{(b^1_1)}^2\right] }}\Big (a^1_1|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D\!+\!b^1_1|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D\nonumber \\&-\,a^1_1|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D+b^1_1|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D\Big ), \end{aligned}$$
(17)

with \(a^1_1=a'b'\), \(b^1_1=a'c'\). Dick transforms the state \(|\varphi '_{ABCD}\rangle '_2\) into the state \(|\varphi '_{ABCD}\rangle '_1\) with a phase-flip operation \(\sigma _z=|H\rangle \langle H|-|V\rangle \langle V|\) on his photon \(D\). The success probability of getting the less-entangled cluster state in Eq. (16) is equal to \({P_1}^1=\frac{2a^4b^2(b^2+c^2)}{(a^4+b^4)(a^2+b^2)}\). The state in Eq. (16) also can be used in the second concentration step. The state in Eq. (14) can also be reused to get the less-entangled cluster state with the same form as that in Eq. (16) but with different parameters by iteration of the process discussed above [from Eqs. (11) to (17)].

Fig. 3
figure 3

a The relation between the success probability \(P^1_\mathrm{\mathrm total}\) of the present ECP for the partially entangled cluster state in the first step and the coefficients \(a\) under the iteration numbers of entanglement concentration \(n = 0, 2, 4\), and 6, respectively. Here we choose the coefficient \(b=1/2\), and \(a\in (0,\sqrt{3}/2)\). b The total success probability \(P_\mathrm{total}^1\) of the first step versus the coefficients \(a\) and \(c\). We choose the iteration number \(n=6\), and the coefficient \(a,c\in (0,1/2)\)

Full size image

In the first step, we calculate the success probability in each iterated round as

$$\begin{aligned}&{P_0}^1=\frac{2a^2(b^2+c^2)}{a^2+b^2},\nonumber \\&{P_1}^1=\frac{2a^4b^2(b^2+c^2)}{(a^4+b^4)(a^2+b^2)},\nonumber \\&{P_2}^1=\frac{2a^8b^6(b^2+c^2)}{(a^8+b^8)(a^4+b^4)(a^2+b^2)},\nonumber \\&\ldots \nonumber \\&{P_n}^1=\frac{2a^{2^{(n+1)}}b^{(2^{(n+1)}-2)}(b^2+c^2)}{\prod _{i=1}^n(a^{2^{(i+1)}}+b^{2^{(i+1)}})}, \end{aligned}$$
(18)

where the subscript 0, 1, 2, ..., \(n\) are the number of iteration, and the superscript 1 means the first concentration step. Therefore, by repeating the entanglement concentration process \(n\) times, the total success probability of the first step is

$$\begin{aligned} P_\mathrm{total}^1={P_0}^1+{P_1}^1+{P_2}^1+ \cdots + {P_n}^1=\sum _{n=0}^{\infty } {P_n}^1. \end{aligned}$$
(19)

The total success probability \(P_\mathrm{total}^1\) of the first step versus the iteration numbers \(n\) of entanglement concentration and the initial coefficient \(a\) is shown in Fig. 3a; here we choose \(b=1/2\) and change \(a \in (0,\sqrt{3}/2)\). We can see form Fig. 3a, \(P_\mathrm{total}^1\) increases as \(a\) increases, when \(0< a \le 1/2\), and interestingly, the success probability \(P_\mathrm{total}^1\) reaches up to the maximum value when \(a=1/2\). But \(P_\mathrm{total}^1\) decreases as \(a\) increases, when \(1/2 \le a < \sqrt{3}/2\). Looking back the Fig. 3a, we also can find that the overall probability of success \(P_\mathrm{total}^1\) increases when increasing the iteration number \(n\). At the beginning, \(P_\mathrm{total}^1\) observably increases as the raising number \(n\) of iterations, but the increasing is indistinctive after the iteration number \(n \ge 6\). If we set \(a=b=c=1/2\) and \(n=0\), \(P_\mathrm{total}^1=1/2\). If we set \(a=b=c=1/2\) and \(n=6\), the success probability \(P_\mathrm{total}^1\) reaches up to 1. On the other hand, the relation between the success probability \(P_\mathrm{total}^1\) and the coefficients \(a\) and \(c\) is shown in Fig. 3b, where we set the iteration number of the entanglement concentration \(n=6\). From Fig. 3b, we find that \(P_\mathrm{total}^1\) increases with the increase in the coefficients \(a\) and \(c\) when \(0< a \le 1/2\) and \(0< c \le 1/2\). \(P_\mathrm{total}^1\longrightarrow 1\) when \(a=b=c=1/2\).

The second step is similar to the first one. After we get the state \(|\Psi ''_{ABCD}\rangle _1\) in Eq. (9), one of the left three, for example Bob, prepares an ancillary single photon \(F\) that is emitted from \(S_2\) and whose initial state is give by

$$\begin{aligned} |\varphi \rangle _F=\frac{1}{\sqrt{{a_1}^2+{b_1}^2}}(b_1|H\rangle _F+a_1|V\rangle _F). \end{aligned}$$
(20)

When the photon \(B\) and photon \(F\) pass the \(\hbox {QND}_2\) as shown in Fig. 1, the combined system evolves as

$$\begin{aligned} |\Phi _{ABCDF}\rangle= & {} \frac{1}{\sqrt{(2{a_1}^2+2{b_1}^2)({a_1}^2+{b_1}^2)}}(a_1b_1|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D|H\rangle _F|\alpha \rangle \nonumber \\&+\,{a_1}^2|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D|V\rangle _F|\alpha e^{i\theta }\rangle \nonumber \\&+\,{b_1}^2|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D|H\rangle _F|\alpha e^{-i\theta }\rangle \nonumber \\&+\,a_1b_1|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D|V\rangle _F|\alpha \rangle \nonumber \\&+\,a_1b_1|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D|H\rangle _F|\alpha \rangle \nonumber \\&+\,{a_1}^2|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D|V\rangle _F|\alpha e^{i\theta } \rangle \nonumber \\&-\,{b_1}^2|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D|H\rangle _F|\alpha e^{-i\theta }\rangle \nonumber \\&-\,a_1b_1|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D|V\rangle _F|\alpha \rangle ). \end{aligned}$$
(21)

If Bob chooses an X-quadrature measurement on the coherent state \(|\alpha \rangle \), he can distinguish the outcomes in two classes with different phase shifts by homodyne–heterodyne measurements. That is, (1) if the coherent state \(|\alpha \rangle \) picks up no phase shift, we can confirm that the system of the single photon \(F\) and the \(|\phi _{ABCD}\rangle \) in the state

$$\begin{aligned} |\Phi '_{ABCDF}\rangle _1= & {} \frac{1}{\sqrt{ 4{a_1}^2{b_1}^2}}(a_1b_1|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D|H\rangle _F\nonumber \\&+\,a_1b_1|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D|V\rangle _F\nonumber \\&+\,a_1b_1|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D|H\rangle _F-a_1b_1|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D|V\rangle _F).\nonumber \\ \end{aligned}$$
(22)

(2) If the coherent state \(|\alpha \rangle \) picks up the phase shift \(\pm \theta \), we can confirm that the system of the single photon \(F\) and the \(|\phi _{ABCD}\rangle \) in the state

$$\begin{aligned} |\Phi '_{ABCDF}\rangle _2= & {} \frac{1}{\sqrt{ 2{a_1}^4+2{b_1}^4}}\Big ({a_1}^2|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D|V\rangle _F\nonumber \\&+\,{b_1}^2|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D|H\rangle _F\nonumber \\&+\,{a_1}^2|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D|V\rangle _F-{b_1}^2|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D|H\rangle _F\Big ).\nonumber \\ \end{aligned}$$
(23)

To realize the partially entangled cluster state concentration, Bob sends photon \(F\) passing though \(\hbox {HWP}_{45}\), and the transformation of photon \(F\) is similar to Eq. (7). Then, the state in Eq. (22) becomes

$$\begin{aligned} |\Phi ''_{ABCDF}\rangle= & {} \frac{1}{\sqrt{8a_1^2b_1^2}}[(a_1b_1|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D+a_1b_1|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D\nonumber \\&+\,a_1b_1|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D-a_1b_1|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D)|H\rangle _F\nonumber \\&+\,(a_1b_1|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D+a_1b_1|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D\nonumber \\&-\,a_1b_1|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D+a_1b_1|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D)|V\rangle _F].\nonumber \\ \end{aligned}$$
(24)

At last, the outcomes are detected by two conventional photon detectors \(D_3\) and \(D_4\). If \(D_3\) fires, we will get

$$\begin{aligned} |\Phi ''_{ABCD}\rangle _1= & {} \frac{1}{2}(|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D+|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D\nonumber \\&+\,|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D-|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D); \end{aligned}$$
(25)

otherwise, if \(D_4\) fires, we will get

$$\begin{aligned} |\Phi ''_{ABCD}\rangle _2= & {} \frac{1}{2}(|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D+|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D\nonumber \\&-|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D+|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D). \end{aligned}$$
(26)

Bob can transform the state \(|\Phi ''_{ABCD}\rangle _2\) into the cluster state \(|\Phi ''_{ABCD}\rangle _1\) with a phase-flip operation on his photon \(B\). The success probability of getting the maximally entangled cluster state \(|\Phi ''_{ABCD}\rangle _1\) is \({P_0}^2=\frac{2b^2c^2}{(b^2+c^2)^2}\). The superscript 2 means the second concentration step, and the subscript 0 is the iteration number. Until now, we have realized the entanglement concentration for partially entangled cluster state with weak cross-Kerr nonlinearity.

In second step, the state in Eq. (23) can also be used to get a maximally entangled cluster state by iteration of the above process from Eqs. (11) to (17). We can calculate the success probability of the each iterated round in the second step.

$$\begin{aligned}&{P_0}^2=\frac{2b^2c^2}{(b^2+c^2)^2},\nonumber \\&{P_1}^2=\frac{2b^4c^4}{(b^4+c^4)(b^2+c^2)^2},\nonumber \\&{P_2}^2=\frac{2b^8c^8}{(b^8+c^8)(b^4+c^4)(b^2+c^2)^2},\nonumber \\&\ldots \nonumber \\&{P_m}^2=\frac{2b^{2^{(m+1)}}c^{2^{(m+1)}}}{(b^2+c^2)\prod _{j=1}^m(b^{2^{(j+1)}}+c^{2^{(j+1)}})}, \end{aligned}$$
(27)

where the subscript 0, 1, 2, ..., \(m\) are the number of iteration, and the superscript 2 means the second concentration step. The total success probability of the second step is

$$\begin{aligned} P_\mathrm{total}^2={P_0}^2+{P_1}^2+{P_2}^2+ \cdots + {P_m}^2=\sum _{m=0}^{\infty } {P_m}^2. \end{aligned}$$
(28)

The total success probability \(P_\mathrm{total}^2\) of the this step versus the iteration numbers \(m\) of entanglement concentration and the initial coefficient \(c\) is shown in Fig. 4a, here we choose \(b=1/2\), and change \(c \in (0, \sqrt{3}/2)\). The relation of \(P_\mathrm{total}^2\) and the coefficients \(a\) and \(c\) is shown in Fig. 4b, where the iteration number of the entanglement concentration \(m=6\). Compared with Fig. 3a, b, similar patterns have been observed in Fig. 4a, b, respectively. That is, if \(a=b=c=1/2\) and \(m=0\), \(P_\mathrm{total}^2=1/2\); If \(a=b=c=1/2\) and \(m=6\), \(P_\mathrm{total}^2=1\). And \(P_\mathrm{total}^2\) increases with the increase inf the coefficients \(a\) and \(c\) when \(0< a \le 1/2\) and \(0< c \le 1/2\), \(P_\mathrm{total}^2\longrightarrow 1\) when \(a=b=c=1/2\).

Fig. 4
figure 4

a The success probability \(P_\mathrm{total}^2\) of the second step for the partially entangled cluster state versus the coefficient \(c\) under the iteration numbers of entanglement concentration \(n = 0, 2, 4\), and 6, respectively. Here we choose the coefficient \(b=1/2\), and \(c\in (0,\sqrt{3}/2)\). b The total success probability \(P_\mathrm{total}^2\) of the second step versus the coefficients \(a\) and \(c\). We choose the iteration number \(n=6\), and the coefficient \(a,c\in (0,1/2)\)

Full size image

3 Entanglement concentration of less-entangled \(4N\)-qubit cluster states

In principle, our ECP proposed in Sect. 2 can be further extended to concentrate the \(4N\)-qubit cluster state with two steps. The less-entangled \(4N\)-qubit cluster state can be written as

$$\begin{aligned} |\phi _{12345\cdots 4N}\rangle= & {} a(|H\rangle _1|H\rangle _2|H\rangle _3|H\rangle _4\cdots |H\rangle _{4N-1}|H\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{4N-1}|H\rangle _{4N}+\cdots \nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{2N}|H\rangle _{2N+1}\cdots |H\rangle _{4N-1}|H\rangle _{4N})\nonumber \\&+\,\frac{ac}{b}(|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{2N}|V\rangle _{2N+1}\cdots |H\rangle _{4N-1}|H\rangle _{4N}\!+\!\cdots \nonumber \\&+\,|V\rangle _1|V\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|H\rangle _{4N-1}|H\rangle _{4N})\nonumber \\&+\,b(|H\rangle _1|H\rangle _2|H\rangle _3|H\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{4N-3}|H\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N}+\cdots \nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{2N}|H\rangle _{2N+1}\cdots |V\rangle _{4N-1}|V\rangle _{4N})\nonumber \\&+\,c(|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{2N}|V\rangle _{2N+1}\cdots |V\rangle _{4N-1}|V\rangle _{4N}+\cdots \nonumber \\&-\,|V\rangle _1|V\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N}), \end{aligned}$$
(29)

where the subscript 1, 2, 3, ..., \(4N\) represents the photons in the cluster state shared by different parties. With the parameters \(2^{(N-1)}(|a|^2+|ac/b|^2+|b|^2+|c|^2)=1\). To obtain a standard maximally entangled \(4N\)-photon cluster state from the state in Eq. (29), for the first step, Dick, who shares the \(4N\)th photon, prepares an ancillary photon \(E\) in the state \(|\varphi \rangle _E=\frac{1}{\sqrt{a^2+b^2}}(b|H\rangle _E+a|V\rangle _E)\), similar to the case in the ECP of a less-entangled four-qubits cluster state. After the single photon \(E\) and the \(4N\)th photon pass through the \(\hbox {QND}_1\), the total state evolves as

$$\begin{aligned} |\Psi _{12345\cdots 4NE}\rangle= & {} \frac{1}{\sqrt{(a^2+b^2)}} [ab(|H\rangle _1|H\rangle _2|H\rangle _3|H\rangle _4\cdots |H\rangle _{4N-1}|H\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{4N-1}|H\rangle _{4N}+\cdots \nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{2N}|H\rangle _{2N+1}\cdots |H\rangle _{4N-1}|H\rangle _{4N})|H\rangle _E|\alpha \rangle \nonumber \\&+\,a^2(|H\rangle _1|H\rangle _2|H\rangle _3|H\rangle _4\cdots |H\rangle _{4N-1}|H\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{4N-1}|H\rangle _{4N}+\cdots \nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{2N}|H\rangle _{2N+1}\cdots |H\rangle _{4N-1}|H\rangle _{4N})|V\rangle _E|\alpha e^{i\theta }\rangle \nonumber \\&+\,ac(|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{2N}|V\rangle _{2N+1}\cdots |H\rangle _{4N-1}|H\rangle _{4N}+\cdots \nonumber \\&+\,|V\rangle _1|V\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|H\rangle _{4N-1}|H\rangle _{4N})|H\rangle _E|\alpha \rangle \nonumber \\&+\,\frac{a^2c}{b}(|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{2N}|V\rangle _{2N+1}\cdots |H\rangle _{4N-1}|H\rangle _{4N}+\cdots \nonumber \\&+\,|V\rangle _1|V\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|H\rangle _{4N-1}|H\rangle _{4N})|V\rangle _E|\alpha e^{i\theta }\rangle \nonumber \\&+\,b^2(|H\rangle _1|H\rangle _2|H\rangle _3|H\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{4N-3}|H\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N}+\cdots \nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{2N}|H\rangle _{2N+1}\cdots |V\rangle _{4N-1}|V\rangle _{4N})|H\rangle _E|\alpha e^{-i\theta }\rangle \nonumber \\&+\,ab(|H\rangle _1|H\rangle _2|H\rangle _3|H\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{4N-3}|H\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N}+\cdots \nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{2N}|H\rangle _{2N+1}\cdots |V\rangle _{4N-1}|V\rangle _{4N})|V\rangle _E|\alpha \rangle \nonumber \\&+\,bc(|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{2N}|V\rangle _{2N+1}\cdots |V\rangle _{4N-1}|V\rangle _{4N}+\cdots \nonumber \\&-\,|V\rangle _1|V\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N})|H\rangle _E|\alpha e^{-i\theta }\rangle \nonumber \\&+\,ac(|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{2N}|V\rangle _{2N+1}\cdots |V\rangle _{4N-1}|V\rangle _{4N}+\cdots \nonumber \\&-\,|V\rangle _1|V\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N})|V\rangle _E|\alpha \rangle ]. \end{aligned}$$
(30)

We choose an X-quadrature measurement on the coherent state \(|\alpha \rangle \). If the coherent state \(|\alpha \rangle \) picks up the phase shift \(\pm \theta \), the whole system collapses to

$$\begin{aligned} |\Psi '_{12345\cdots 4NE}\rangle _1= & {} \frac{1}{\sqrt{(a^2+b^2)}} [ab(|H\rangle _1|H\rangle _2|H\rangle _3|H\rangle _4\cdots |H\rangle _{4N-1}|H\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{4N-1}|H\rangle _{4N}+\cdots \nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{2N}|H\rangle _{2N+1}\cdots |H\rangle _{4N-1}|H\rangle _{4N})|H\rangle _E\nonumber \\&+\,ac(|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{2N}|V\rangle _{2N+1}\cdots |H\rangle _{4N-1}|H\rangle _{4N}\!+\!\cdots \nonumber \\&+\,|V\rangle _1|V\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|H\rangle _{4N-1}|H\rangle _{4N})|H\rangle _E\nonumber \\&+\,ab(|H\rangle _1|H\rangle _2|H\rangle _3|H\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{4N-3}|H\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N}+\cdots \nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{2N}|H\rangle _{2N+1}\cdots |V\rangle _{4N-1}|V\rangle _{4N})|V\rangle _E\nonumber \\&+\,ac(|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{2N}|V\rangle _{2N+1}\cdots |V\rangle _{4N-1}|V\rangle _{4N}+\cdots \nonumber \\&-\,|V\rangle _1|V\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N})|V\rangle _E]. \end{aligned}$$
(31)

Next, the photon \(E\) passes through the \(\hbox {HWP}_{45}\) and \(\hbox {PBS}_1\), and finally, it will be detected by photon detectors \(D_1\) and \(D_2\). If the detection result is \(|H\rangle _E\), we will get

$$\begin{aligned} |\Psi ''_{12345\cdots 4N}\rangle= & {} \frac{1}{\sqrt{2^{(N-1)}(a^2b^2+a^2c^2)}} [ab(|H\rangle _1|H\rangle _2|H\rangle _3|H\rangle _4\cdots |H\rangle _{4N-1}|H\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{4N-1}|H\rangle _{4N}+\cdots \nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{2N}|H\rangle _{2N+1}\cdots |H\rangle _{4N-1}|H\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{2N}|V\rangle _{2N+1}\cdots |H\rangle _{4N-1}|H\rangle _{4N}+\cdots \nonumber \\&+\,|V\rangle _1|V\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|H\rangle _{4N-1}|H\rangle _{4N})\nonumber \\&+\,ac(|H\rangle _1|H\rangle _2|H\rangle _3|H\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{4N-3}|H\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N}+\cdots \nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{2N}|H\rangle _{2N+1}\cdots |V\rangle _{4N-1}|V\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{2N}|V\rangle _{2N+1}\cdots |V\rangle _{4N-1}|V\rangle _{4N}+\cdots \nonumber \\&-\,|V\rangle _1|V\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N})]. \end{aligned}$$
(32)

Similar to the process in the first step of the less-entangled \(4N\)-qubit cluster state concentration, in the second step, the \(2N\)th photon’s holder Bob prepares an ancillary photon \(F\) in the state \(|\varphi \rangle _F=\frac{1}{\sqrt{a^2(b^2+c^2)}}(ac|H\rangle _F+ab|V\rangle _F)\) and sends the \(2N\)th photon and \(F\) passing through the \(\hbox {QND}_2\). We choose the items corresponding to the coherent state \(|\alpha \rangle \) picking up no phase shift; then, the photon \(F\) will be sent to passes through \(\hbox {HWP}_{45}\) and \(\hbox {PBS}_2\) and finally detected by \(D_3\) and \(D_4\). If the measurement result is \(|H\rangle _F\), we obtain the maximally entangled \(4N\)-qubit cluster state as follows

$$\begin{aligned} |\phi _{12345\cdots 4N}\rangle= & {} \frac{1}{2^N} (|H\rangle _1|H\rangle _2|H\rangle _3|H\rangle _4\cdots |H\rangle _{4N-1}|H\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{4N-1}|H\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|H\rangle _{4N-1}|H\rangle _{4N}+\cdots \nonumber \\&+\,|V\rangle _1|V\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|H\rangle _{4N-1}|H\rangle _{4N}+\cdots \nonumber \\&+\,|H\rangle _1|H\rangle _2|H\rangle _3|H\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |H\rangle _{4N-3}|H\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N}\nonumber \\&+\,|H\rangle _1|H\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N}+\cdots \nonumber \\&-\,|V\rangle _1|V\rangle _2|V\rangle _3|V\rangle _4\cdots |V\rangle _{4N-3}|V\rangle _{4N-2}|V\rangle _{4N-1}|V\rangle _{4N}). \end{aligned}$$
(33)

When the iteration numbers \(n=0\) and \(m=0\), the total success probability is \(\frac{2^{-2N}a^2b^2c^2}{(a^2+b^2)(b^2+c^2)}\). We can also get a high success probability by iterating the concentration process in each steps as shown in Sect. 2.

4 Discussion and summary

By far, we have presented an ECP for distilling the maximally entangled cluster state from a less-entangled cluster state. In our protocol, only a less-entangled cluster state and two auxiliary single photons are required to complete the task. Furthermore, this protocol does not require sophisticated single-photon detector as the QND has the function of a photon number detector. Actually, it should be noted that the linear optical elements in the current ECPs are common in current experiment conditions, such as PBSs, \(\hbox {HWP}_{45}\hbox {s}\), and conventional photon detectors, which have been widely used in ECPs [54, 55], but not ideal. For the success probability to our calculation, we assume the efficiency of the linear optical elements is perfect.

Fig. 5
figure 5

a The total success probability \(P_\mathrm{total}\) of the present ECP for the partially entangled cluster state versus the coefficient \(a\) under the iteration numbers of entanglement concentration \(n\) and \(m\). Here we choose the coefficient \(b=1/2\), and \(a\in (0,\sqrt{3}/2)\). b The total success probability \(P_\mathrm{total}\) of the present ECP for the partially entangled cluster state versus the iteration number \(n\) and \(m\) of each steps. Here, we choose the coefficients \(a=1/2\), \(b=1/2\), and \(c=1/2\), change the iteration number \(n,m\in (0,10)\)

Full size image

We calculate the total success probability of the protocol while the iteration number is \(n\) and \(m\) in each steps, respectively.

$$\begin{aligned} P_\mathrm{total}= & {} P_0^1\left( P_0^2+P_1^2+\cdots +P_m^2\right) +P_1^1\left( P_0^2+P_1^2+\cdots +P_m^2\right) \nonumber \\&+\cdots +P_n^1\left( P_0^2+P_1^2+\cdots +P_m^2\right) \nonumber \\= & {} \sum _{n=1}^\infty P_n^1\sum _{m=1}^\infty P_m^2. \end{aligned}$$
(34)

When \(a=b=1/2\), the initial state is

$$\begin{aligned} |\phi _{ABCD}\rangle= & {} \frac{1}{2}(|H\rangle _A|H\rangle _B|H\rangle _C|H\rangle _D+|V\rangle _A|V\rangle _B|H\rangle _C|H\rangle _D\nonumber \\&+|H\rangle _A|H\rangle _B|V\rangle _C|V\rangle _D-|V\rangle _A|V\rangle _B|V\rangle _C|V\rangle _D) \end{aligned}$$
(35)

and the success probability of the ECP reaches up to

$$\begin{aligned} P_\mathrm{total}= & {} \sum _{n=1}^n P_n^1\sum _{m=1}^m P_m^2\nonumber \\= & {} \left( \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots \right) \left( \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots \right) \nonumber \\= & {} 1. \end{aligned}$$
(36)

The total success probability \(P_\mathrm{total}\) of the ECP versus the iteration numbers \(n\), \(m\), and the initial coefficient \(a\) is shown in Fig. 5a; here we set \(b=1/2\) and change \(a \in (0, \sqrt{3}/2)\). From Fig. 5a, we can see that \(P_\mathrm{total}\) increases as the coefficient \(a\) increases, when \(0< a \le 1/2\), and \(P_\mathrm{total}^1\) decreases as \(a\) increases, when \(1/2 \le a < \sqrt{3}/2\). If we set \(a=1/2\), the overall success probability \(P_\mathrm{total}\) reaches up to the maximum value. On the other hand, we plot the overall success probability \(P_\mathrm{total}\) of the present ECP for the partially entangled cluster state versus the iteration numbers \(n\) and \(m\) in Fig. 5b, and here we choose the coefficients \(a=b=c=1/2\). We can see from Fig. 5b that \(P_\mathrm{total}\) increases when increasing the iteration numbers \(n\) and \(m\). For example, we set \(a=b=c=1/2\), (1) \(P_\mathrm{total}=1/4\), when the iteration number \(n=m=0\); (2) \(P_\mathrm{total}=1/2\), when \(n=0\) and \(m=6\); (3) \(P_\mathrm{total}=1/2\), when \(n=6\) and \(m=0\); (4) \(P_\mathrm{total}=1\), when \(n=6\) and \(m=6\).

In our protocol, with the help of the weak cross-Kerr nonlinearity, we can check the photon number without destroying the photons. If and only if the QNDs are used to detect the number of photon in polarization modes, the conventional photon detectors that only distinguish the vacuum and nonvacuum Fock number states are enough for present ECP, the parties are not required to possess the sophisticated single-photon detectors. However, we must note that a clean cross-Kerr nonlinearity in the optical single-photon system is still quite a controversial assumption with current technology. Fortunately, the QND in our ECP does not require a large nonlinearity, and it works for small values of the cross-Kerr coupling, which decreases the difficulty of its implementation. As far as we know, the largest natural cross-Kerr nonlinearities are extremely weak (\(\chi ^{(3)} \approx 10^{-22} m^2 V^{-2}\)) [56, 57]. In 2002, Kok et al. [57] argued that the Kerr phase shift while operating in the optical single-photon system is about \(\tau \approx 10^{-18}\). Cross-Kerr nonlinearity of \(\tau \approx 10^{-5}\) can be obtained with electromagnetically induced transparent materials. But, in 2006, Shapiro [58] showed that the single-photon Kerr nonlinearities without help in quantum computation. In 2010, Gea-Banacloche [59] presented an approximate analytical solution combined with numerical calculations, for a system of two single-photon wave packets interacting via localized Kerr medium which is an ideal is impossible at present. In 2011, series broader studies of the cross-Kerr nonlinearity are being discussed. He et al. [40] discussed the cross-Kerr nonlinearity between continuous-mode coherent state and single photons. They believed that their work constituted significant progress in making the treatment of coherent state and single-photon interactions more realistic. Feizpour et al. [60] expanded a cross-Kerr phase shift to an observable value with the help of weak measurement. Zhu et al. [61] studied linear and nonlinear propagations of probe and signal pulses in a multiple quantum-well structure with a four-level, double-\(\Lambda \)-type configuration and showed that slow, mutually matched group velocities and giant Kerr nonlinearity of the probe and the signal pulses may be achieved with nearly vanishing optical absorption. So in the condition of current technology, the present ECP can be satisfied with the weak cross-Kerr nonlinearity. In addition, the detectors \(D_{1,2,3,4}\) in the present scheme are only used to absorb the photon passed through the transmission channels, so the sensitivity and dark counts of the detectors does not influence the efficiency of the scheme. Hence, these detectors \(D_{1,2,3,4}\) can even be replaced with other absorption objects. While the detection efficiency of \(D_{1,2,3,4}\) will affect the performance of the ECP, that is because the successful achievement of the scheme is dependent on the detection results of \(D_{1,2,3,4}\). Nevertheless, \(D_{1,2,3,4}\) are only required to distinguish the vacuum and nonvacuum state rather than distinguish the number of the photons, which thus decreases the requirements of the photon detection in practical realization.

Compared with the previous scheme in Ref. [33], the present one has the following advantages. First of all, the initial cluster state in this paper has different form with that in Ref. [33]. That is, there are three parameters in Eq. (2) in our protocol, so, the initial state of this manuscript has one more parameter than the protocol in Ref. [33]. The obvious advantage is that the more parameters in the state, the more information can be taken by the state. Therefore, our protocol can straight be generalized to arbitrary partially entangled \(4N\)-photon cluster states concentration easily. Secondly, the present ECP could be completed in two steps shown in Sect. 2. We provide a detailed analysis for different contributions of the success probability in the two steps which is shown in Figs. 3 and 4, respectively. Thirdly, the protocol is not just employ the linear optical elements, the cross-Kerr nonlinearity is also be used. In fact, the key to this manuscript is the QND which constructed with weak cross-Kerr nonlinearity. This is the main difference between this manuscript and the previous scheme in Ref. [33]. Fourthly, the cross-Kerr nonlinearity, which is a powerful tool for constructing QND, and has the potential available of being able to condition the evolution of our system without necessarily destroying the single photons. This property makes our protocol can be reused for further concentration. The ECP has the higher success probability since the discarded items in the protocol can be reused for further concentration. Numerical simulation demonstrates that by iterating the entanglement concentration process \(n=m=6\) times, the ECP has the approximate maximal success probability 100 %. Till now, to improve the imperfect of the success probability, the method of iterating the entanglement concentration process has been used in many schemes [29, 31, 32].

In summary, we have put forward an efficient ECP for distilling the maximally entangled \(4N\)-qubit cluster state from a less-entangled cluster state. In the present ECP, we only require a less-entangled cluster state and two auxiliary single photons to complete the task. The ECP has several advantages: First, the devices of the scheme are composed of some simple linear optical elements, single polarization photons, and conventional photon detectors, which have been widely used to entangle photons. In particular, the similar optical setups have been used to successfully prepare GHZ states of photons in experiment [62]. Second, with the help of the weak cross-Kerr nonlinearities, we can reach a higher success probability to realize the ECP for partially entangled cluster states by iterating the entanglement concentration process \(n=m=6\) times. Therefore, our ECP may be useful and convenient in the current quantum information processing.