Skip to main content
SpringerLink
Log in

Uncertainty principle guarantees genuine source of intrinsic randomness

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

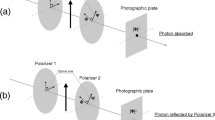
The Born’s rule introduces intrinsic randomness to the outcomes of a measurement performed on a quantum mechanical system. But, if the system is prepared in the eigenstate of an observable, then the measurement outcome of that observable is completely predictable, and hence, there is no intrinsic randomness. On the other hand, if two incompatible observables are measured (either sequentially on a particle or simultaneously on two identical copies of the particle), then uncertainty principle guarantees intrinsic randomness in the subsequent outcomes independent of the preparation state of the system. In this article, we show that this is true not only in quantum mechanics but for any no-signaling probabilistic theory. Also the minimum amount of intrinsic randomness that can be guaranteed for arbitrarily prepared state of the system is quantified by the amount of (un)certainty.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Heisenberg, W.: Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik/The Actual Content of Quantum Theoretical Kinematics and Mechanics. Z. Phys. 43, 172 (1927). (translated and repented into English) The Physical Content of Quantum Kinematics and Mechanics. In: Wheeler, J.A., Zurek W.H. (eds.) Quantum Theory of Measurement, pp. 62. Princeton University Press, N.J. (1983)

  2. Busch, P., Shilladay, C.: Complementarity and uncertainty in Mach-Zehnder interferometry and beyond. Phys. Rep. 435, 1–31 (2006)

    Article  ADS  Google Scholar 

  3. Busch, P., Heinonen, T., Lahti, P.: Heisenberg’s uncertainty principle. Phys. Rep. 452, 155–176 (2007)

    Article  ADS  Google Scholar 

  4. Born, M.: Quantenmechanik der StoßBvorgänge. Z. Phys. 38, 803–827 (1926)

    Article  ADS  Google Scholar 

  5. Born, M.: Das Adiabatenprinzip in der Quantenmechanik/The Adiabatic Principle in Quantum Mechanics. Z. Phys. 40, 167 (1926)

    Article  ADS  MATH  Google Scholar 

  6. Oppenheim, J., Wehner, S.: The uncertainty principle determines the nonlocality of quantum mechanics. Science 330, 1072–1074 (2010)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  7. Robertson, H.P.: The uncertainty principle. Phys. Rev. 34, 163–164 (1929)

    Article  ADS  Google Scholar 

  8. Carruthers, P., Nieto, M.M.: Phase and angle variables in quantum mechanics. Rev. Mod. Phys. 40, 411–440 (1968)

    Article  ADS  Google Scholar 

  9. Louisell, W.H.: Amplitude and phase uncertainty relations. Phys. Lett. 7(1), 60–61 (1963)

    Article  MathSciNet  ADS  Google Scholar 

  10. Bialynicki-Birula, I., Mycielski, J.: Uncertainty relations for information entropy in wave mechanics. Commun. Math. Phys. 44(2), 129–132 (1975)

    Article  MathSciNet  ADS  Google Scholar 

  11. Deutsch, D.: Uncertainty in quantum measurements. Phys. Rev. Lett. 50, 631–633 (1983)

    Article  MathSciNet  ADS  Google Scholar 

  12. Kraus, K.: Complementary observables and uncertainty relations. Phys. Rev. D 35, 3070–3075 (1987)

    Article  MathSciNet  ADS  Google Scholar 

  13. Maassen, H., Uffink, J.B.M.: Generalized entropic uncertainty relations. Phys. Rev. Lett. 60, 1103–1106 (1988)

    Article  MathSciNet  ADS  Google Scholar 

  14. Wehner, S., Winter, A.: Entropic uncertainty relations—a survey. N. J. Phys. 12, 025009 (2010)

    Article  MathSciNet  Google Scholar 

  15. Hardy, L.: Quantum theory from five reasonable axioms. arXiv:0101012[quant-ph] (2001)

  16. Barrett, J.: Information processing in generalized probabilistic theories. Phys. Rev. A 75, 032304 (2007)

    Article  ADS  Google Scholar 

  17. Barnum, H., Barrett, J., Leifer, M., Wilce, A.: Generalized no-broadcasting theorem. Phys. Rev. Lett. 99, 240501 (2007)

    Article  ADS  Google Scholar 

  18. Barnum, H., Barrett, J., Leifer, M., Wilce, A.: Teleportation in general probabilistic theories. arXiv:0805.3553 (2008)

  19. Barnum, H., Gaebler, C. P., Wilce, A.: Ensemble steering, weak self-duality, and the structure of probabilistic theories. arXiv:0912.5532 (2009)

  20. Barnum, H., Wilce, A.: Information processing in convex operational theories. arXiv:0908.2352 (2009)

  21. Barnum, H., et al.: Entropy and information causality in general probabilistic theories. New J. Phys. 12, 033024 (2010)

    Article  MathSciNet  ADS  Google Scholar 

  22. Chiribella, G., DArian, G.M., Perinotti, P.: Informational derivation of quantum theory. Phys. Rev. A 84, 012311 (2011)

    Article  ADS  Google Scholar 

  23. Masanes, L., Mueller, M.P.: A derivation of quantum theory from physical requirements. New J. Phys. 13, 063001 (2011)

    Article  ADS  Google Scholar 

  24. Pfister, C.: One simple postulate implies that every polytopic state space is classical. arXiv:1203.5622 (2012)

  25. Pironio, S., et al.: Random numbers certified by Bell?s theorem. Nature 464, 1021 (2010)

    Article  ADS  Google Scholar 

  26. Acin, A., Massar, S., Pironio, S.: Randomness versus nonlocality and entanglement. Phys. Rev. Lett. 108, 100402 (2012)

    Article  ADS  Google Scholar 

  27. Koenig, R., Renner, R., Schaffner, C.: The operational meaning of min- and max-entropy. IEEE Trans. Inf. Theory 55, 4337 (2009)

    Article  MathSciNet  Google Scholar 

  28. Berta, M., Christandl, M., Colbeck, R., Renes, J.M., Renner, R.: The uncertainty principle in the presence of quantum memory. Nat. Phys. 6, 659–662 (2010)

    Article  Google Scholar 

  29. Prevedel, R., Hamel, D.R., Colbeck, R., Fisher, K., Resch, K.J.: Experimental investigation of the uncertainty principle in the presence of quantum memory and its application to witnessing entanglement. Nat. Phys. 7, 757–761 (2011)

    Article  Google Scholar 

  30. D’Arian, G.M., Manessia, F., Perinottia, P.: Spooky action-at-a-distance in general probabilistic theories. Phys. Lett. A 376, 2926–2930 (2012)

    Article  MathSciNet  ADS  Google Scholar 

  31. Brandenburger, A., Yanofsky, N.: A classification of hidden-variable properties. J. Phys. A 41, 42 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  32. Bell, J.S.: On the problem of hidden variables in quantum mechanics. Rev. Mod. Phys. 38, 447–452 (1966)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  33. Mermin, N.D.: Hidden variables and the two theorems of John Bell. Rev. Mod. Phys. 65, 803–815 (1993)

    Article  MathSciNet  ADS  Google Scholar 

  34. Harrigan, N., Spekkens, R.W.: Einstein, incompleteness, and the epistemic view of quantum states. Found. Phys. 40, 125–157 (2010)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  35. Popescu, S., Rohrlich, D.: Quantum nonlocality as an axiom. Found. Phys. 24, 379–385 (1994)

    Article  MathSciNet  ADS  Google Scholar 

  36. Spekkens, R.W.: Evidence for the epistemic view of quantum states: A toy theory. Phys. Rev. A 75, 032110 (2007)

    Article  ADS  Google Scholar 

  37. Benioff, P.: Possible strengthening of the interpretative rules of quantum mechanics. Phys. Rev. D 7, 3603–3609 (1973)

    Article  ADS  Google Scholar 

  38. Benioff, P.A.: Models of Zermelo Frankel set theory as carriers for the mathematics of physics. I. J. Math. Phys. 17, 618 (1976)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  39. Benioff, P.A.: Models of Zermelo Frankel set theory as carriers for the mathematics of physics. II. J. Math. Phys. 17, 629 (1976)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  40. Banik, M., Gazi, M.D.R., Ghosh, S.: Degree of complementarity determines the nonlocality in quantum mechanics. Phys. Rev. A 87, 052125 (2013)

    Article  ADS  Google Scholar 

  41. Colbeck, R., Renner, R.: Free randomness can be amplified. Nat. Phys. 8, 450–453 (2012)

    Article  Google Scholar 

  42. Gallego, R., Masanes, L., Torre, G., Dhara, C., Aolita, L., Acin, A.: Full randomness from arbitrarily deterministic events. arXiv:1210.6514 (2012).

  43. Knuth, D.: The Art of Computer Programming 2: Seminumerical Algorithms. Addison-Wesley, Reading, Massachusetts (1981)

    MATH  Google Scholar 

  44. Stefanov, A., Gisin, N., Guinnard, O., Guinnard, L., Zbinden, H.: Optical quantum random number generator. J. Mod. Opt 47, 595–598 (2000)

    ADS  Google Scholar 

  45. Dynes, J.F., Yuan, Z.L., Sharpe, A.W., Shields, A.J.: A high speed, postprocessing free, quantum random number generator. Appl. Phys. Lett. 93, 031109 (2008)

    Article  ADS  Google Scholar 

  46. Atsushi, U., et al.: Fast physical random bit generation with chaotic semiconductor lasers. Nat. Photonics 2, 728–732 (2008)

    Article  Google Scholar 

Download references

Acknowledgments

We like to thank G.Kar for many simulating discussion and giving suggestions. TC thanks Council of Scientific and Industrial Research, India, for financial support through Senior Research Fellowship (Grant No. 09/093(0134)/2010). MB like to acknowledge discussion with A. Rai, Md. R. Gazi and S. Das. PP thank Council of Scientific and Industrial Research, India, for financial support.

Author information

Authors and Affiliations

  1. Physics and Applied Mathematics Unit, Indian Statistical Institute, 203 B.T. Road, Kolkata, 700108, India

    Trina Chakraborty & Manik Banik

  2. Department of Physics, University of Kalyani, Kalyani, 741235, India

    Pinaki Patra

Authors
  1. Trina Chakraborty
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Manik Banik
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Pinaki Patra
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Manik Banik.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chakraborty, T., Banik, M. & Patra, P. Uncertainty principle guarantees genuine source of intrinsic randomness. Quantum Inf Process 13, 839–848 (2014). https://doi.org/10.1007/s11128-013-0695-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-013-0695-5

Keywords

Search

Navigation