Abstract
This paper proposes a new construction of quantum low-density parity check (LDPC) codes that belong to the class of general stabilizer (non-CSS) codes. The method constructs a binary check matrix \(A=(A_{1}|A_{2})\) associated with the stabilizer generators of a quantum LDPC code. The binary check matrix is obtained from a large bipartite graph built by combining several small bipartite graphs called seed graphs. Computer simulation results show that the proposed code has similar or better performance than other quantum LDPC codes, and can be improved by exploiting the degenerate effect of quantum error-correcting codes.








Similar content being viewed by others
Notes
The normalizer of \(\mathcal G \), denoted \(N(\mathcal G )\), is defined as a subgroup of \(\mathcal P _{n}\) consisting of all elements \(E\) of \(\mathcal P _{n}\) such that \(Eg_{i}E^{\dagger }\in \mathcal G \) for all \(g_{i}\in \mathcal G \) [29].
In particular, the degenerate effect of a quantum LDPC code with small minimum distance is stronger than that of a quantum LDPC code with large minimum distance.
While the connection between seed graphs is bidirectional, we use the term source and target for ease of reference
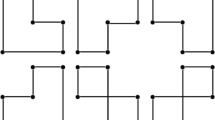
A binary matrix that describes a bipartite graph is called the biadjacency matrix [44].
The \(\eta \) seed graphs should all be different from each other.
As mentioned in Sect. 3.2, the matrices \(C_{i}\) and \({C_{i}}^{^{\prime }}\) are identical.
References
Aly, S.A.: A class of quantum LDPC codes derived from latin squares and combinatorial design. Tech. rep., Department of Computer Science, Texas A &M University (2007)
Aly, S.A.: A class of quantum LDPC codes constructed from finite geometries. In: Proceedings of IEEE Globecom (2008). http://arXiv.org/abs/0712.4115
Aly, S.A., Klappenecker, A., Sarvepalli, P.K.: Primitive quantum BCH codes over finite fields. In: IEEE International Symposium on Information Theory, pp. 1114–1118 (2006)
Brun, T., Devetak, I., Hsieh, M.H.: Catalytic quantum error correction. http://arxiv.org/abs/quant-ph/0608027 (2006)
Brun, T., Devetak, I., Hsieh, M.H.: Correcting quantum errors with entanglement. Science 314(5798), 436–439 (2006)
Calderbank, A.R., Rains, E.M., Shor, P.W., Sloane, N.J.A.: Quantum error correction and orthogonal geometry. Phys. Rev. Lett. 78(3), 405–408 (1997)
Calderbank, A.R., Rains, E.M., Shor, P.W., Sloane, N.J.A.: Quantum error correction via codes over \(GF(4)\). IEEE Trans. Inf. Theory 44, 1369–1387 (1998)
Calderbank, A.R., Shor, P.W.: Good quantum error-correcting codes exist. Phys. Rev. A 54, 1098–1105 (1995)
Camara, T., Ollivier, H., Tillich, J.P.: A class of quantum LDPC codes: construction and performances under iterative decoding. In: IEEE International Symposium on Information Theory, pp. 811–815. IEEE Information Theory Society (2007)
Davey, M.C., Mackay, D.J.C.: Low-density parity-check codes over \(GF(q)\). IEEE Commun. Lett. 2(6), 165–167 (1998)
Djordjevic, I.B.: Quantum ldpc codes from balanced incomplete block designs. IEEE Commun. Lett. 12(5), 389–391 (2008)
Fujiwara, Y., Clark, D., Vandendriessche, P., Boech, M.D., Tonchev, V.D.: Entanglement-assisted quantum low-density parity-check codes. Phys. Rev. A 82(4), 042338 (2010)
Gallager, R.G.: Low-density parity-check codes. IRE Transactions on Information Theory pp. 21–28 (1962)
Gottesman, D.: Class of quantum error-correcting codes saturating the quantum hamming bound. Phys. Rev. A 54(3), 1862–1868 (1996)
Gottesman, D.: Stabilizer codes and quantum error correction. Ph.D. thesis, California Institute of Technology (1997)
Grassl, M., Beth, T.: Quantum BCH codes. http://arxiv.org/abs/quant-ph/9910060 (1999)
Grassl, M., Geiselmann, W., Beth, T.: Quantum reed-solomon codes. In: Proceedings Applied Algebra, Algebraic Algorithms and Error-Correcting Codes (AAECC-13), pp. 231–244. Springer (1999)
Grover, L.K.: A fast quantum mechanical algorithm for database search. Proceedings of the twenty-eighth annual ACM symposium on Theory of, Computing, pp. 212–219 (1996)
Hagiwara, M., Imai, H.: Quantum quasi-cyclic LDPC codes. http://arxiv.org/abs/quant-ph/0701020 (2010)
Hsieh, M.H., Brun, T.A., Devetak, I.: Entanglement-assisted quantum quasicyclic low-density parity-check codes. Phys. Rev. A 79(3), 032340 (2009)
Hsieh, M.H., Devetak, I., Brun, T.: General entanglement-assted quantum error-correcting codes. Phys. Rev. A 76(6), 062313 (2007)
Hsieh, M.H., Yen, W.T., Hsu, L.Y.: High performance entanglement-assisted quantum LDPC codes need little entanglement. IEEE Trans. Inf. Theory 57(3), 1761–1769 (2011)
Laflamme, R., Miquel, C., Paz, J.P., Zurek, W.H.: Perfect quantum error correcting code. Phys. Rev. Lett. 77(1), 198–201 (1996)
Luby, M.G., Mitzenmacher, M., Shokrollahi, M.A., Spielman, D.A.: Analysis of low density codes and improved designs using irregular graphs. In: Proceedings of the thirthieth annual ACM symposium on Theory of computing, no. 10 in STOC ’98, pp. 249–258. ACM, New York, NY, USA (1998)
Mackay, D.J.C.: Good error-correcting codes based on very sparse matrices. IEEE Trans. Inf. Theory 45(2), 399–431 (1999)
Mackay, D.J.C.: Information Theory, Inference, and Learning algorithms. Cambridge University Press, Cambridge (2003)
Mackay, D.J.C., Mitchison, G., McFadden, P.L.: Sparse-graph codes for quantum error correction. IEEE Trans. Inf. Theory 50(10), 2315–2330 (2004)
Mackay, D.J.C., Neal, R.M.: Near shannon limit performance of low density parity check codes. Electron. Lett. 32(18), 1645–1646 (1996)
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)
Ollivier, H., Tillich, J.P.: Desription of a quantum convolutional code. Phys. Rev. Lett. 91, 177902 (2003)
Ollivier, H., Tillich, J.P.: Quantum convolutional codes: fundamentals. http://arxiv.org/abs/quant-ph/0401134 (2004)
Postol, M.S.: A proposed quantum low density parity check code. http://arxiv.org/abs/quant-ph/0108131
Poulin, D., Chung, Y.: On the iterative decoding of sparse quantum codes. Quantum Inf. Comput. 8(10), 987–1000 (2008)
Poulin, D., Tillich, J.P., Ollivier, H.: Quantum serial turbo codes. IEEE Trans. Inf. Theory 55(6), 2776–2798 (2009)
Richardson, T.J., Shokrollahi, M.A., Urbanke, R.L.: Design of capacity-approaching irregular Low-Density Parity-Check codes. IEEE Trans. Inf. Theory 47(2), 619–637 (2001)
Richardson, T.J., Urbanke, R.L.: The capacity of Low-Density Parity-Check codes under message-passing decoding. IEEE Trans. Inf. Theory 47(2), 599–618 (2001)
Shor, P.W.: Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52(4), R2493–R2496 (1995)
Shor, P.W.: Fault-tolerant quantum computation. In: Proceedings of the 37th Annual Symposium on Foundations of Computer Science, pp. 56–65. IEEE Computer Society, Washington, DC, USA (1996)
Shor, P.W.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 26(5), 1484–1509 (1997)
Steane, A.: Multiple-particle interference and quantum error correction. Proc. R. Soc. A 452(1954), 2551–2577 (1996)
Tan, P., Li, J.: Efficient quantum stabilizer codes: LDPC and LDPC-convolutional constructions. IEEE Trans. Inf. Theory 56(1), 476–491 (2010)
Tanner, R.M.: A recursive approach to low complexity codes. IEEE Trans. Inf. Theory 27(5), 533–547 (1981)
Wang, Y.J., Sanders, B.C., Bai, B.M., Wang, X.M.: Enhanced feedback iterative decoding of sparse quantum codes. IEEE Trans. Inf. Theory 58(2), 1231–1241 (2012)
WIKIPEDIA: Adjacency matrix. http://en.wikipedia.org/wiki/Adjacency_matrix
Acknowledgments
This work was supported by System Biology Infrastructure Establishment Grant, GIST and Unmanned technology Research Center at KAIST, originally funded by DAPA, ADD, KOREA.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Block matrix for a seed graph and a connection type
In this section, we describe the binary matrix representation of the seed graphs and the connection types described in Sect. 3.2. They are used to prove Theorem 2 in the next section.
Definition 2
(Seed graph matrix \({\varvec{S}}_{\varvec{s}}\)) The matrix of size \(m\times n\) for describing the seed graph defined by Eq (12) is:
As mentioned in Sect. 3.2, if the \(i\)th and \(j\)th seed graphs are connected, then the manner in which the \(c\)-nodes in \(\mathsf S _{i}\) are linked to the \(v\)-nodes in \(\mathsf S _{j}\) follows one of \(\delta \) connection types. Each connection type can be represented by the following matrix called the connection type matrix.
Definition 3
(Connection type matrix \({\varvec{C}}_{\varvec{t}}\)) The matrix of size \(m\times n\) specifying the indices of the \(c\)-nodes and \(v\)-nodes of the seed graphs involved in the connection is
This definition follows the combination process in Eq. (13). The connection type matrix \(C_{t}\) indicates that all the \(c\)-nodes in a source seed graph are mapped to the \((m\cdot t)\sim (m\cdot t+m-1)\)th \(v\)-nodes in a target seed graph.
Appendix 2: Conditions for a regular code
In this section, we prove Theorem 2. After first providing some background (see Sect. 7.1), we will prove the theorem (see Sect. 7.2).
1.1 Backgrounds for the proof
In Sect. 3.2, we showed that the position of a seed graph \(\mathsf S _{s}\) in a model matrix \(M_{i}\) can be coincident with that of a connection type \(C_{t}\) depending on the chosen construction parameters, \(\eta \) and \((a_{l}, b_{l})\)s. In addition, two different connection types \(C_{t}\) and \(C_{t^{\prime }}\) for \(t\ne t^{\prime }\) can be located in the same position. As we have mentioned, these phenomena, denoted by \(S_{s}\boxplus C_{t}\) and \(C_{t}\boxplus C_{t^{\prime }}\), are closely related to the regularity of the resulting code.
Before describing the phenomena in detail, we remark that the operation “\(\boxplus \)” corresponds to the logical OR operation defined in Table 2. The operation “\(\boxplus \)” used in this paper indicates the connections between nodes of a source seed graph and a target seed graph. In this case, additional connections between the already linked nodes do not eliminate the existing connection. Therefore, the operation “\(\boxplus \)” is the logical OR operation.
In what follows, we show the relationship between the regularity of the proposed code and the phenomena \(S_{s}\boxplus C_{t}\) and \(C_{t}\boxplus C_{t^{\prime }}\). Suppose that a seed graph \(\mathsf S _{s}\) and a connection type \(C_{t}\) are located in the same position of a model matrix \(M_{1}, M_{1}[i, j]=S_{s}\boxplus C_{t}\). Then the block matrix of \(A_{1}\) associated with \(M_{1}[i, j]\) is the result of the logical OR operation between the seed graph matrix \(S_{s}\) and the connection type matrix \(C_{t}\), and this may become irregular according to the chosen seed graph. Although the combination of a seed graph matrix \({S}_{s}\) and a connection type matrix \(C_{t}\) defined in Sect. 6 does not lead to an irregular block matrix, we give an example using another bipartite graph for the seed graph below. Let us define a seed graph \(S_{s}\) as follows:
If we fix the size of a seed graph as \((2, 4)\), then the matrix \(S_{s}\) by Eq. (25) is as follows:
Since \(\delta \) (\(n/m\)) is 2, there are \(2\) connection types, \(C_{0}\) and \(C_{1}\). By Definition 3, these connection types have the following matrices:
Thus, considering \(S_{s}\boxplus C_{1}\), we have
The resulting matrix is irregular, and \(S_{s}\boxplus C_{0}\) is also irregular. As shown above, combining \(S_{s}\) and \(C_{t}\) can lead to an irregular block matrix for \(A_{i}\).
Definition 4
(SC collision) If \(M_{i}[i, j]\) is a combination of \(S_{s}\) and \(C_{t}\) for any \(t\) where \(0\le t\le \delta -1\), then the associated block matrix of \(A_{i}\) is irregular. In addition, if \(M_{1}[i,j]=S_{s}\) and \(M_{2}[i,j]=C_{t}\) (or vice versa), then the associated matrices \(A_{1}\) and \(A_{2}\) introduce irregular stabilizer generators in the Pauli group. We call these combinations of \(S\) and \(C_{t}\) the SC collision, which induces an irregular code.
To discuss the phenomenon \(C_{t}\boxplus C_{t^{\prime }}\), we only focus on the \(0\)th row of each model matrix. Suppose that \(\mu _{i}\) is the \(0\)th row of \(M_{i}\):
Let us consider the following example. Suppose that we combine \(\eta \) seed graphs with the construction parameters \(\lambda =2\) and \(\{(4, 3), (4, 7)\}\). Then the combination process for \(A_{1}\) is as follows:
from the combination process in Eq. (13). If \(t\) is 0, then the connection \(\mathsf S _{i}\longrightarrow ~\mathsf S _{i+4}\) is repeated twice regardless of the value of \(\eta \). Otherwise, the repetition of the connection depends on the value of \(\eta \). If \(\eta \) is 14, then \(\mu _{1}\) is as follows:
where \(C_{i}\) and \(C_{i}^{^{\prime }}\) are connections by (4, 3) and (4, 7) respectively.Footnote 6 Then, by definition, \(C_{0}\boxplus C_{0}^{^{\prime }}=C_{0}\boxplus C_{0} = C_{0}\), and therefore \(\mu _{1}\) is
While there are two \(C_{1}\)s in \(\mu _{1}\), the number of \(C_{0}\)s is one. Thus \(\mu _{1}\) leads to an irregular matrix \(M_{1}\). As a consequence, a combination of \(C_{t}\) and \(C_{t^{\prime }}\) for \(t\ne t^{\prime }\) can induce an irregular model matrix according to the value of \(\eta \).
Definition 5
(CC collision) If \(C_{t}\) and \(C_{t^{\prime }}\) for \(t\ne t^{\prime }\) are located in the same position of a model matrix \(M_{i}\), the associated binary check matrix \(A=(A_{1}|A_{2})\) induces an irregular code. In addition, if \(M_{1}[i, j]=C_{t}\) and \(M_{2}[i, j]=C_{t^{\prime }}\) or vice versa, then the associated binary check matrix \(A\) induces irregular stabilizer generators in the Pauli group. We call these combinations of \(C_{t}\)s the CC collision.
1.2 Proof of Theorem 2
Proof
Regarding the relationship between the binary check matrix \(A=(A_{1}|A_{2})\) in the proposed framework and stabilizer generators, there are two conditions to be fulfilled for a regular code.
-
Each matrix \(A_{i}\) must be a regular matrix.
-
The regularity of \(A_{i}\) must be preserved when the binary check matrix \(A=(A_{1}|A_{2})\) is in the Pauli group.
These two conditions can be satisfied if SC collisions and CC collisions do not happen in a model matrix \(M_{i}\). Suppose that we have the connection rule in Eq. (13), and that \(\mu _{i}\) is the \(0\)th row of \(M_{i}\). Then the positions of \(S_{s}\) and \(C_{t}\) in \(\mu _{i}\) are summarized in Table 3, and the following can be easily verified by checking the table.
-
1.
If \(0\ne (a_{l}+b_{l}\cdot t)\), there are no SC collisions in each \(\mu _{i}\).
-
2.
If \(0\ne (\eta /2+a_{l}+b_{l}\cdot t)\), there are no SC collisions in a combination of \(\mu _{1}\) and \(\mu _{2}\).
-
3.
If \((a_{l}+b_{l}\cdot t)\ne (a_{l^{\prime }}+b_{l^{\prime }}\cdot t)\) for \(l\ne l^{^{\prime }}\), there are no CC collisions in each \(\mu _{i}\).
-
4.
If \((a_{l}+b_{l}\cdot t)\ne (\eta /2+a_{l^{\prime }}+b_{l^{\prime }}\cdot t)\) for \(l\ne l^{^{\prime }}\), there are no CC collisions in a combination of \(\mu _{1}\) and \(\mu _{2}\).
Note that all variables are over \(0\le l, l^{\prime } \le \lambda -1\) and \(0\le t\le \delta -1\), and both sides of the above four equations are calculated modulo \(\eta \). The first two conditions are related to the first condition in Theorem 2. The other two conditions are associated with the second and third conditions in Theorem 2 respectively. \(\square \)
Rights and permissions
About this article
Cite this article
Hwang, Y., Chung, Y. & Jeon, M. A class of quantum low-density parity check codes by combining seed graphs. Quantum Inf Process 12, 2219–2239 (2013). https://doi.org/10.1007/s11128-012-0519-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11128-012-0519-z