Abstract
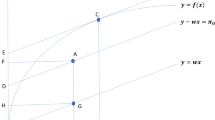
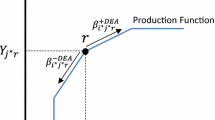
The directional distance function encompasses Shephard’s input and output distance functions and also allows nonradial projections of the assessed firm onto the frontier of the technology in a preassigned direction. However, the criteria underlying the choice of its associated directional vector are numerous. When market prices are observed and firms have a profit maximizing behavior, it seems natural to choose as the directional vector that projecting inefficient firms towards profit maximizing benchmarks. Based on that choice of directional vector, we introduce the directional profit efficiency measure and show that, in this general setting, profit inefficiency can be categorized as either technical, for firms situated within the interior of the technology, or allocative, for firms lying on the frontier. We implement and illustrate the analytical model by way of Data Envelopment Analysis techniques, and introduce the necessary optimization programs for profit inefficiency measurement.

Similar content being viewed by others
Notes
Also, the approach could be extended to a free disposal hull setting.
We note that we could render (8) more flexible by letting it solve for the directional vector \( ( {g_{x}^{T} ,g_{y}^{T} } ) \in R_{ + + }^{N} \times R_{ + + }^{M} \), including pg T y + wg T x = 1 and g T x , g T y ≥ 0 as additional constraints, thereby projecting the evaluated firm in the direction leading to the reference benchmark with the highest possible profit compatible with the non-negativity constraint, i.e., the firm is forced to move northwesterly.
Moreover, the case of multiple profit maximizing benchmarks could also arise when input and output prices are not the same across firms (see, for example, Portela and Thanassoulis 2007).
References
Aparicio J, Ruiz JL, Sirvent I (2007) Closest targets and minimum distance to the Pareto-efficient frontier in DEA. J Prod Anal 28:209–218
Asmild M, Paradi JC, Reese DN, Tam F (2007) Measuring overall efficiency and effectiveness using DEA. Eur J Oper Res 178:305–321
Ball E, Färe R, Grosskopf S, Nehring R (2001) Productivity of the U.S. agricultural sector: the case of undesirable outputs. In: Hulten CR, Dean ER, Harper MJ (eds) New developments in productivity analysis. University of Chicago Press, Chicago, pp 541–586
Banker RD, Maindiratta A (1988) Nonparametric analysis of technical and allocative efficiencies in production. Econometrica 56(6):1315–1332
Bogetoft P, Färe R, Obel B (2006) Allocative efficiency of technically inefficient production units. Eur J Oper Res 168:450–462
Chambers R (1998) Input and output indicators. In: Färe R, Grosskopf S, Russell RR (eds) Index numbers: essays in honour of Sten Malmquist. Kluwer Academic Publishers, Boston, pp 241–271
Chambers R, Chung Y, Färe R (1996) Benefit and distance functions. J Econom Theory 70:407–419
Chambers R, Chung Y, Färe R (1998) Profit, directional distance functions and Nerlovian efficiency. J Optim Theory Appl 95(2):351–364
Charnes A, Cooper WW, Golany B, Seiford L (1985) Foundations of data envelopment analysis for Pareto-Koopmans efficient empirical production functions. J Econom 30:91–107
Chavas J-P, Cox TM (1999) A generalized distance function and the analysis of production efficiency. South Econ J 66(2):295–318
Cooper WW, Park KS, Pastor JT (1999) RAM: a range adjusted measure of inefficiency for use with additive models, and relations to other models and measures in DEA. J Prod Anal 11:5–42
Cooper WW, Pastor JT, Aparicio J, Borras F (2011) Decomposing profit inefficiency in DEA through the weighted additive model. Eur J Oper Res 212:411–416
Cyert RM, March JG (1963) A behavioral theory of the firm. Prentice Hall, Englewood Cliffs, NJ
Färe R, Grosskopf S (2000a) Notes on some inequalities in economics. Econ Theor 15(1):227–233
Färe R, Grosskopf S (2000b) Theory and applications of directional distance functions. J Prod Anal 13(2):93–103
Färe R, Primont D (1995) Multi-output production and duality: theory and applications. Kluwer Academic Publishers, Dordrecht
Färe R, Grosskopf S, Whittaker G (2007) Network DEA. In: Zhu J, Cook WD (eds) Modeling data irregularities and structural complexities in data envelopment analysis, chapter 12. Springer, Berlin
Farrell M (1957) The measurement of productive efficiency. J R Stat Soc Ser A 120(3):253–281
Leibenstein H (1966) Allocative efficiency vs. X-efficiency. Am Econ Rev 56:392–415
Luenberger DG (1992) New optimality principles for economic efficiency and equilibrium. J Optim Theory Appl 75:221–264
Portela M, Thanassoulis E (2005) Profitability of a sample of Portuguese bank branches and its decomposition into technical and allocative components. Eur J Oper Res 162(3):850–866
Portela M, Thanassoulis E (2007) Developing a decomposable measure of profit efficiency using DEA. J Oper Res Soc 58:481–490
Portela M, Borges PC, Thanassoulis E (2003) Finding closest targets in non-oriented DEA models: the case of convex and non-convex technologies. J Prod Anal 19:251–269
Ruiz JL, Sirvent I (2011) A DEA approach to derive individual lower and upper bounds for the technical and allocative components of the overall profit efficiency. J Oper Res Soc 62(11):1907–1916
Shephard R (1970) Theory of cost and production functions. Princeton University Press, New Jersey
Acknowledgments
We are grateful to the participants and discussants at the International Workshop on Efficiency and Productivity in honor of Prof. Knox Lovell (October 4–5, 2010, Elche, Spain). We acknowledge financial support from the Ministerio de Ciencia e Innovacion, Spain, and the Conselleria de Educacion, Generalitat Valenciana, for supporting this research with grants MTM2009-10479 and ACOMP/2011/115, respectively. Finally, we are also indebted to two referees for their comments and suggestions that have contributed to improving this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
A previous version was published in Economics Working Papers Series, Universidad Autónoma de Madrid, Department of Economics, No. 2010/09.
Rights and permissions
About this article
Cite this article
Zofio, J.L., Pastor, J.T. & Aparicio, J. The directional profit efficiency measure: on why profit inefficiency is either technical or allocative. J Prod Anal 40, 257–266 (2013). https://doi.org/10.1007/s11123-012-0292-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11123-012-0292-0