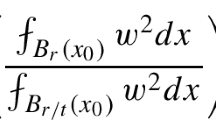Boundary Doubling Inequality and Nodal sets of Robin and Neumann eigenfunctions

Abstract

We investigate the doubling inequality and upper bounds of nodal sets for Robin and Neumann eigenfunctions on the boundary and in the interior of the domain. Most efforts are devoted to the sharp boundary doubling inequality with new and novel quantitative global Carleman estimates. We are able to obtain the sharp upper bounds for boundary nodal sets of Neumann eigenfunctions.

Appendix

In the Appendix, we first construct polar coordinates for equations with Lipschitz metrics in Eq. 2.9, then we obtain the doubling inequalities on the double manifold. Most of the arguments in the Appendix are kind of known and scattered in the literature. We present the details for the conveniences of the readers. Without loss of generality, we consider the construction of normal coordinates at origin. Starting from a ball $\mathbb B_{\delta }$ in local coordinates, for the metric $\tilde {g}_{ij}$ in Eq. 2.9, we introduce a “radial” coordinate and a conformal change metric $\hat {g}_{ij}$. Let

$$ r=r(x)=(\tilde{g}_{ij}(0)x_{i} x_{j})^{\frac{1}{2}} $$

(5.41)

and

$$ \hat{g}_{ij}(x)= \tilde{g}_{ij}(x){\hat{\psi}}(x), $$

(5.42)

where

$$ {\hat{\psi}}(x)= \tilde{g}^{kl}(x)\frac{\partial r}{\partial x^{k}}\frac{\partial r}{\partial x^{l}} $$

(5.43)

for x≠ 0 and $(\tilde {g}^{ij})=(\tilde {g}_{ij})^{-1}$ is the inverse matrix. In the whole paper, we adopt the Einstein notation. The summation over index is understood. We assume the uniform ellipticity condition holds in $\mathbb B_{\delta }$ for

$$ {\Lambda}_{1}\|\xi\|^{2} \leq \sum\limits^{n}_{i,j=1} \tilde{g}_{ij}(x)\xi_{i}\xi_{j}\leq {\Lambda}_{2}\|\xi\|^{2} $$

for some positive constant Λ₁ and Λ₂ depending only on Ω. Then $\hat {\psi }$ is bounded above and below satisfying

$$ \frac{{\Lambda}_{1}}{{\Lambda}_{2}}\leq \hat{\psi}\leq \frac{{\Lambda}_{2}}{{\Lambda}_{1}}. $$

(5.44)

We can also see that $\hat {\psi }$ is Lipschitz continuous. With these auxiliary quantities, the following replacement of geodesic polar coordinates are constructed in [3]. In the geodesic ball $\hat { \mathbb B}_{\hat {r}_{0}}=\{ x\in \tilde {\Omega }| r(x)\leq \hat {r}_{0}\},$ the following properties hold:

• (i) $\hat {g}_{ij}(x)$ is Lipschitz continuous;

• (ii) $\hat {g}_{ij}(x)$ is uniformly elliptic with $\frac {{{\Lambda }_{1}^{2}}}{ {\Lambda }_{2} }\|\xi \|^{2}\leq \hat {g}_{ij}(x)\xi _{i}\xi _{j}\leq \frac {{{\Lambda }_{2}^{2}}}{ {\Lambda }_{1}}\|\xi \|^{2}.$

• (iii) Let ${\Sigma } =\partial \hat { \mathbb B}_{\hat {r}_{0}}$. We can parametrize $\hat { \mathbb B}_{\hat {r}_{0}} \backslash \{0\}$ by the polar coordinate r and θ, with r defined by Eq. 5.41 and θ = (θ₁,⋯θ_n− 1) be the local coordinates on Σ. In these polar coordinates, the metric can be written as

  $$ \hat{g}_{ij}(x) dx^{i} dx^{j}= dr^{2}+ r^{2} \hat{\gamma}_{ij} d\theta^{i} d\theta^{j} $$

  (5.45)

  with $\hat {\gamma }_{ij}=\frac {1}{r^{2}} \hat {g}_{kl}(x) \frac {\partial x^{k}}{\partial \theta ^{i}}\frac {\partial x^{l}}{\partial \theta ^{j}}$.

• (iv) There exists a positive constant M depending on $\tilde {g}_{ij}$ such that for any tangent vector ξ_j ∈ T_θ(Σ),

  $$ \begin{array}{@{}rcl@{}} |\frac{\partial \hat{\gamma}_{ij}(r, \theta)}{\partial r} \xi^{i} \xi^{j}|\leq M| \hat{\gamma}_{ij}(r, \theta)\xi^{i} \xi^{j}|. \end{array} $$

  (5.46)

Let $\hat {\gamma }=\det { (\hat {\gamma }_{ij})}$. Then Eq. 5.46 implies that

$$ |\frac{\partial \ln \sqrt{\hat{\gamma}}}{\partial r}| \leq CM. $$

(5.47)

The existence of the coordinates (r, θ) allows us to pass to “geodesic polar coordinates”. In particular, $r(x)=(\tilde {g}_{ij}(0)x_{i} x_{j})^{\frac {1}{2}}$ is the geodesic distance to the origin in the metric $\hat {g}_{ij}$. In the new metric $\hat {g}_{ij}$, the Laplace-Beltrami operator is

$$\triangle_{\hat{g}}=\frac{1}{\sqrt{\hat{g} }} \frac{\partial}{\partial x_{i}}(\hat{g}^{ij}\sqrt{ \hat{g}} \frac{\partial}{\partial x_{j}} ),$$

where $\hat {g}= \det (\hat {g}_{ij})$. If $\bar u$ is a solution of Eq. 2.9, then $\bar u$ is locally the solution of the equation

$$ \triangle_{\hat{g}} \bar u +\hat{b}(x)\cdot\nabla \bar u+ \hat{c}(x) \bar u=0 \quad \text{in} \ \hat{\mathbb B}_{\hat{r}_{0}}, $$

(5.48)

where

$$ \left\{ \begin{array}{lll} &\hat{b}_{i}=\frac{2-n}{2\hat{\psi}^{2}} \tilde{g}^{ij} \frac{\partial \hat{\psi} }{\partial x_{j}}+\frac{1}{\hat{\psi}}\tilde{b}_{i}, \\ &\hat{c}(x)=\frac{\tilde{c}(x)}{\hat{\psi}}. \end{array} \right. $$

(5.49)

By the properties of $\hat {\psi }$, we can see $\hat {c}(x)$ is Lipschitz continuous. Since the term $\frac {2-n}{2\hat {\psi }^{2}} \tilde {g}^{ij} \frac {\partial \hat {\psi } }{\partial x_{j}}$ in $\hat {b}_{i}$ is only continuous and does not depend on either α or λ, it can be ignored in the future quantitative estimates for doubling inequality or nodal sets. The major term $\frac {1}{\hat {\psi }}\tilde {b}_{i}$ is Lipschitz continuous. From the conditions in Eq. 2.10, we still write the conditions for $\hat {b}$ and $\hat {c}$ as

$$ \left\{ \begin{array}{lll} \|\hat {b}\|_{W^{1,\infty}(\hat{\mathbb B}_{\hat{r}_{0}})}\leq C (|\alpha|+1), \\ \|\hat { c}\|_{W^{1,\infty}(\hat{\mathbb B}_{\hat{r}_{0}})}\leq C (\alpha^{2}+|\lambda|). \end{array} \right. $$

(5.50)

For simplicity, we may write $\triangle _{\hat {g}}$ or △_g as △ if the metric is understood. Since the geodesic balls or half balls under different metrics are comparable, we write all as $\mathbb B_{r}(x)$ or $\mathbb B^{+}_{r}(x)$ centered at x with radius r. The rest of section is to show the doubling inequality on the double manifold. Let r = r(y) be the Riemannian distance from origin to y. Our major tools to get the three-ball theorem and doubling inequality are the quantitative Carleman estimates. Carleman estimates are weighted integral inequalities with a weight function e^τψ, where ψ usually satisfies some convex condition. We construct the weight function ψ as follows. Set

$$\psi(y)=-g(\ln r(y)),$$

where $g(t)=t+\log t^{2}$ for $-\infty <t <T_{0}$, and T₀ is negative with |T₀| large enough. One can check that

$$ \lim_{t \to -\infty}-e^{-t} g^{\prime\prime}(t)=\infty \quad \text{and} \quad \lim_{t \to -\infty} g^{\prime}(t)=1. $$

(5.51)

Define

$$ \psi_{\tau}(y)=e^{\tau \psi(y)}. $$

(5.52)

We state the following quantitative Carleman estimates. The similar Carleman estimates with lower bound of the parameter τ have been obtained in e.g. [4, 10, 48]. Interested readers may refer to them for the proof of the following proposition.

Proposition 1

There exist positive constants C₁, C₀ and small r₀, such that for $v\in C^{\infty }_{0}(\mathbb B_{r_{0}} \backslash \mathbb B_{\rho }),$ and

$$\tau>C_{1}(1+|\alpha|+\sqrt{|\lambda|}),$$

one has

$$ \begin{array}{@{}rcl@{}} C_{0}\|r^{2} \psi_{\tau}\big(\triangle v +\hat{b}(y)\cdot\nabla v+ \hat{c}(y) v\big)\|^{2}&\geq& \tau^{3}\|\psi_{\tau} {(\log r)}^{-1} v \|^{2} +\tau\|r \psi_{\tau} {(\log r)}^{-1}\nabla v \|^{2} \\ &&+ \tau \rho \|r^{-\frac{1}{2}}\psi_{\tau} v \|^{2}. \end{array} $$

(5.53)

The ∥⋅∥_r or ∥⋅∥ norm in the whole paper denotes the L² norm over $\mathbb B_{r}(0)$ if not explicitly stated. Specifically, $\|\cdot \|_{\mathbb B_{r}(y))}$ for short denotes the L² norm on the ball $\mathbb B_{r}(y)$. Thanks to the quantitative Carleman estimates, it is a standard way to derive a quantitative three-ball theorem. Let $\bar u$ be the solutions of the second order elliptic (5.48). We apply such Carleman estimates with $v=\eta \bar u$, where η is an appropriate smooth cut-off function, and then select an appropriate choice of the parameter τ. The statement of the quantitative three-ball theorem is as follows.

Lemma 1

There exist positive constants $\bar r_{0}$, C which depend only on Ω and 0 < β < 1 such that, for any $0<R<\bar r_{0}$, the solutions $\bar u$ of Eq. 5.48 satisfy

$$ \|\bar u \|_{\mathbb B_{2R}(x_{0})}\leq e^{C(|\alpha|+\sqrt{|\lambda|})} \|\bar u \|^{\beta}_{\mathbb B_{R}(x_{0})} \|\bar u \|^{1-\beta}_{\mathbb B_{3R}(x_{0})} $$

(5.54)

for any $x_{0}\in \tilde {\Omega }$.

Since the proof of three-ball theorem is kind of standard by the applications of quantitative Carleman estimates (5.53). We skip the details. The readers may also refer to Proposition 1 for similar proofs.

Let $\|u\|_{L^{2}({\Omega })}=1$. Because of the even extension, we may write

$$\|\bar u\|_{L^{2}(\tilde{\Omega})}=2.$$

Set $\bar x$ be the point where

$$ \|\bar u\|_{L^{2}(\mathbb B_{\hat{r}_{0}}(\bar x))}=\max_{x\in \tilde{\Omega}} \|\bar u\|_{L^{2}(\mathbb B_{\hat{r}_{0}}(x))} $$

for some $0<\hat {r}_{0}< \frac {\bar r_{0}}{8}$. The compactness of $\tilde {\Omega }$ implies that

$$\|\bar u\|_{L^{2}(\mathbb B_{\hat{r}_{0}}(\bar x))}\geq C_{\hat{r}_{0}}$$

for some $C_{\hat {r}_{0}}$ depending on $\tilde {\Omega }$ and $\hat {r}_{0}$. From the quantitative three-ball inequality (5.54), at any point x ∈Ω, one has

$$ \|\bar u\|_{L^{2}(\mathbb B_{{\hat{r}_{0}}/2}(x))}\geq e^{-C(|\alpha|+\sqrt{|\lambda|})} \|\bar u\|^{\frac{1}{\beta}}_{L^{2}(\mathbb B_{{\hat{r}_{0}}}(x))}. $$

(5.55)

Let l be a geodesic curve between $\hat {x}$ and $\bar x$, where $\hat {x}$ is any point in $\tilde {\Omega }$. Define $x_{0}=\hat {x}, \cdots , x_{m}=\bar x$ such that x_i ∈ l and $\mathbb B_{\frac {\hat {r}_{0}}{2}}(x_{i+1})\subset \mathbb B_{{\hat {r}_{0}}}(x_{i})$ for i from 0 to m − 1. The number of m depends only on $diam (\tilde {\Omega })$ and $\hat {r}_{0}$. The properties of (x_i)_1≤i≤m and the inequality (5.55) imply that

$$ \begin{array}{@{}rcl@{}} \|\bar u\|_{L^{2}(\mathbb B_{{\hat{r}_{0}}/2}(x_{i}))}\geq e^{-C(|\alpha|+\sqrt{|\lambda|})} \|\bar u\|^{\frac{1}{\beta}}_{L^{2}(\mathbb B_{{\hat{r}_{0}}/2}(x_{i+1}))}. \end{array} $$

(5.56)

Iterating the argument to get to $\bar x$, we obtain that

$$ \begin{array}{@{}rcl@{}} \|\bar u\|_{L^{2}(\mathbb B_{{\hat{r}_{0}}/2}(\hat{x}))}&\geq& e^{-C_{\hat{r}_{0}}(|\alpha|+\sqrt{|\lambda|})} C_{\hat{r}_{0}}^{\frac{1}{\beta^{m}}} \\ &\geq& e^{-C_{\hat{r}_{0}}(|\alpha|+\sqrt{|\lambda|})} \|\bar u\|_{L^{2}(\tilde{\Omega})}. \end{array} $$

(5.57)

Let $A_{R, \ 2R}=(\mathbb B_{2R}(x_{0})\backslash \mathbb B_{R}(x_{0}))$ for any $x_{0}\in \tilde {\Omega }$. Then there exists $\mathbb B_{{\hat {r}_{0}}/2}(\hat {x})\subset A_{ \hat {r}_{0}, \ 2\hat {r}_{0}}$ for some $\hat {x}\in A_{2\hat {r}_{0}, \ \hat {r}_{0}}$. Thus, by Eq. 5.57,

$$ \| \bar u\|_{L^{2}(A_{\hat{r}_{0}, \ 2\hat{r}_{0}} )}\geq e^{-C_{\hat{r}_{0}}(|\alpha|+\sqrt{|\lambda|})} \| \bar u\|_{L^{2}(\tilde{{\Omega}})}. $$

(5.58)

With aid of the quantitative Carleman estimates (5.53) and the inequality (5.58), using the argument as the proof of Lemma 3, we are ready to derive the doubling inequality as follows.

Proof of Proposition 1

Let $R=\frac {\bar r_{0}}{8}$, where $\bar r_{0}$ is the fixed constant in the three-ball inequality in Eq. 5.54. Choose $0<\rho <\frac {R}{24}$, which can be chosen to be arbitrarily small. Define a smooth cut-off function 0 < η < 1 as follows,

• η(r) = 0 if r(x) < ρ or r(x) > 2R,

• η(r) = 1 if HCode $\frac {3\rho }{2}<r(x)<R$,

• $|\nabla \eta |\leq \frac {C}{\rho }$ if $\rho <r(x)<\frac {3\rho }{2}$,

• |∇²η|≤ C if R < r(x) < 2R.

We substitute $v=\eta \bar u$ into the Carleman estimates (5.53) and consider the elliptic (5.48). It follows that

$$ \begin{array}{@{}rcl@{}} \tau^{\frac{3}{2}}\| (\log r)^{-1} e^{\tau \psi}\eta \bar u \|+ \tau^{\frac{1}{2}} \rho^{\frac{1}{2}} \| r^{-\frac{1}{2}} e^{\tau \psi}\eta \bar u \| & \leq& C\| r^{2} e^{\tau \psi}(\triangle_{\hat{g}} (\eta\bar u)+ \hat{b}(x) \cdot \nabla (\eta\bar u)+ \hat{c}(x) \eta \bar u )\| \\ & \leq& C\| r^{2} e^{\tau \psi}(\triangle \eta \bar u +2\nabla\eta\cdot \nabla v+\hat{b}\cdot \nabla \eta \bar u )\|. \end{array} $$

Thanks to the properties of η and the fact that τ > 1, we get that

$$ \begin{array}{@{}rcl@{}} \| (\log r)^{-1} e^{\tau \psi} \bar u \|_{\frac{R}{2}, \frac{2R}{3}}+ \| e^{\tau \psi} \bar u \|_{\frac{3\rho}{2}, 4\rho} &\leq& C (\| e^{\tau \psi} \bar u \|_{\rho, \frac{3\rho}{2}}+\| e^{\tau \psi} \bar u\|_{R, 2R} ) \\ &&+ C(\rho \| e^{\tau \psi} \nabla \bar u \|_{\rho, \frac{3\rho}{2}}+ R\| e^{\tau \psi} \nabla \bar u \|_{R, 2R}) \\ &&+ C(|\alpha|+1) (\rho \| e^{\tau \psi} \bar u \|_{\rho, \frac{3\rho}{2}}+ R\| e^{\tau \psi} \bar u \|_{R, 2R} ). \end{array} $$

Since R < 1 is a fixed constant and ρ < 1, we get that

$$ \begin{array}{@{}rcl@{}} \| e^{\tau \psi} \bar u \|_{\frac{R}{2}, \frac{2R}{3}}+ \| e^{\tau \psi} \bar u \|_{\frac{3\rho}{2}, 4\rho} &\leq& C(|\alpha|+1) (\| e^{\tau \psi} \bar u \|_{\rho, \frac{3\rho}{2}}+\| e^{\tau \psi} \bar u \|_{R, 2R} ) \\ &&+ C(\delta \| e^{\tau \psi} \nabla \bar u \|_{\rho, \frac{3\rho}{2}}+ R\| e^{\tau \psi} \nabla \bar u \|_{R, 2R}). \end{array} $$

Using the radial and decreasing property of ψ yields that

$$ \begin{array}{@{}rcl@{}} e^{\tau \psi(\frac{2R}{3})}\| \bar u \|_{\frac{R}{2}, \frac{2R}{3}}+ e^{\tau \psi({4\rho})} \| \bar u \|_{\frac{3\rho}{2}, 4\rho} &\leq &C (|\alpha|+1) (e^{\tau \psi(\rho) }\| \bar u \|_{\rho, \frac{3\rho}{2}}+e^{\tau \psi(R) }\| \bar u \|_{R, 2R} ) \\ &&+ C(\rho e^{\tau \psi(\rho)} \| \nabla \bar u \|_{\rho, \frac{3\rho}{2}}+ Re^{\tau\psi(R)}\| \nabla \bar u \|_{R, 2R}). \end{array} $$

For the Eq. 5.48, it is known that the Caccioppoli type inequality

$$ \|\nabla \bar u \|_{(1-a)r}\leq \frac{C(|\alpha|+\sqrt{|\lambda|})}{r}\| \bar u \|_{r} $$

(5.59)

holds with any 0 < a < 1. With the help of the Caccioppoli type inequality (5.59), we have

$$ \begin{array}{@{}rcl@{}} e^{\tau \psi(\frac{2R}{3})}\| \bar u \|_{\frac{R}{2}, \frac{2R}{3}}+ e^{\tau \psi({4\rho})} \| \bar u \|_{\frac{3\rho}{2}, 4\rho} &\leq C (|\alpha|+\sqrt{|\lambda|}) (e^{\tau \psi(\rho) }\| \bar u \|_{2\rho}+e^{\tau \psi(R)}\| \bar u \|_{3R}). \end{array} $$

(5.60)

Adding the term $e^{\tau \psi ({4\rho })} \|\bar u \|_{\frac {3\rho }{2}}$ to both sides of last inequality and taking ψ(ρ) > ψ(4ρ) into account yields that

$$ \begin{array}{@{}rcl@{}} e^{\tau \psi(\frac{2R}{3})}\| \bar u \|_{\frac{R}{2}, \frac{2R}{3}}+ e^{\tau \psi({4\rho})} \| \bar u \|_{4\rho} &\leq C (|\alpha|+\sqrt{|\lambda|}) (e^{\tau \psi(\rho) }\| \bar u \|_{2\rho}+e^{\tau\psi(R)}\| \bar u \|_{3R}). \end{array} $$

(5.61)

We choose τ such that

$$C(|\alpha|+\sqrt{|\lambda|})e^{\tau\psi(R)}\|\bar u \|_{3R}\leq \frac{1}{2}e^{\tau\psi(\frac{2R}{3})} \|\bar u \|_{\frac{R}{2}, \frac{2R}{3}}. $$

To achieve it, we need to have

$$ \tau\geq \frac{1}{\psi(\frac{2R}{3})-\psi(R)}\ln \frac{ 2C(|\alpha|+\sqrt{|\lambda|}) \|\bar u \|_{3R}}{ \|\bar u \|_{\frac{R}{2}, \frac{3R}{2}}}. $$

Then, we can absorb the second term on the right hand side of Eq. 5.60 into the left hand side,

$$ \begin{array}{@{}rcl@{}} e^{\tau \psi(\frac{2R}{3})}\| \bar u \|_{\frac{R}{2}, \frac{2R}{3}}+ e^{\tau \psi({4\rho})} \| \bar u \|_{4\rho} \leq C (|\alpha|+\sqrt{|\lambda|}) e^{\tau \psi(\rho) }\| \bar u \|_{2\rho}. \end{array} $$

(5.62)

To apply the Carleman estimates (5.53), we have assumed that $\tau \geq C(|\alpha |+\sqrt {|\lambda |})$. Therefore, to have such τ, we select

$$\tau=C(|\alpha|+\sqrt{|\lambda|})+ \frac{1}{\psi(\frac{2R}{3})-\psi(R)}\ln \frac{ 2C(|\alpha|+\sqrt{|\lambda|}) \|\bar u \|_{3R}}{ \|\bar u \|_{\frac{R}{2}, \frac{3R}{2}}}. $$

Dropping the first term in (5.62), we get that

$$ \begin{array}{@{}rcl@{}} \|\bar u\|_{4\rho}&\leq& C(|\alpha|+\sqrt{|\lambda|})\exp\{ \big(\frac{1}{\psi(\frac{2R}{3})-\psi(R)}\ln \frac{ 2C(|\alpha|+\sqrt{|\lambda|}) \|\bar u \|_{3R}}{ \|\bar u \|_{\frac{R}{2}, \frac{3R}{2}}} \big) \big(\psi(\rho)-\psi(4\rho)\big) \\ & +&C(|\alpha|+\sqrt{|\lambda|}) \}\|\bar u \|_{2\rho} \\ &\leq& e^{C (|\alpha|+\sqrt{|\lambda|})} (\frac{\|\bar u \|_{3R}}{ \|\bar u \|_{\frac{R}{2}, \frac{3R}{2}}})^{C} \|\bar u \|_{2\rho}, \end{array} $$

(5.63)

where we have used the condition that

$$ \beta_{1}^{-1}<\psi(\frac{2R}{3})-\psi(R)<\beta_{1}, $$

$$ \beta_{2}^{-1}< \psi(\rho)-\psi(4\rho)<\beta_{2} $$

for some positive constants β₁ and β₂ independent on R or ρ.

Let $\hat {r}_{0}=\frac {R}{2}$ be fixed in Eq. 5.58. With aid of Eq. 5.58, we derive that

$$ \frac{\|\bar u \|_{{L^{2}(\mathbb B_{3 R}})}}{ \|\bar u\|_{{{L^{2}(A_{\frac{R}{2}, \ \frac{3R}{2}})}}}}\leq e^{C(|\alpha|+\sqrt{|\lambda|})}. $$

Therefore, it follows from Eq. 5.63 that

$$ \|\bar u \|_{L^{2}(\mathbb B_{4\rho})}\leq e^{C(|\alpha|+\sqrt{|\lambda|})} \|\bar u \|_{L^{2}(\mathbb B_{2\rho})}. $$

Choosing $\rho =\frac {r}{2}$, we get the doubling inequality

$$ \|\bar u \|_{L^{2}(\mathbb B_{2r})}\leq e^{C(|\alpha|+\sqrt{|\lambda|})} \|\bar u \|_{L^{2}(\mathbb B_{r})} $$

(5.64)

for $r\leq \frac {R}{12}$. If $r\geq \frac { R}{12}$, from Eq. 5.57,

$$ \begin{array}{@{}rcl@{}} \|\bar u \|_{L^{2} (\mathbb B_{r})}&\geq& \|\bar u \|_{L^{2}(\mathbb B_{\frac{ R}{12}})} \\ &\geq& e^{-C_{R}(|\alpha|+\sqrt{|\lambda|})}\|\bar u \|_{L^{2}({\Omega})} \\ &\geq& e^{-C_{R}(|\alpha|+\sqrt{|\lambda|})}\|\bar u \|_{L^{2}(\mathbb B_{2r})}. \end{array} $$

(5.65)

Together with Eqs. 5.64 and 5.65, we obtain the doubling estimates

$$ \|\bar u \|_{L^{2}(\mathbb B_{2r})}\leq e^{C(|\alpha|+\sqrt{|\lambda|})} \|\bar u \|_{L^{2}(\mathbb B_{r})} $$

(5.66)

for any r > 0, where C only depends on the double manifold $\tilde {\Omega }$. By the translation invariant of the arguments, the proof of Eq. 2.11 is derived. □