1 Introduction

In educational research, diametrical views can be found regarding the subject-specific strengths and weaknesses of learners. While a number of researchers emphasize the role of general ability and posit that students performing successfully in one domain are more likely to be high-achieving in another domain (e.g. Reilly 2012; Rindermann 2007), others stress the role of subject-specific learning opportunities and suggest that students exhibit strengths in some domains and at the same time have weaknesses in other domains (e.g. Marsh and Hau 2004; Wang, Eccles, and Kenny 2013). Although a considerable amount of literature has been published on individual differences of learners and their academic performances, few researchers have focused on comparison of student learning outcomes across different subjects. However, cross-subject comparison provides a fundamentally different perspective on students’ overall and subject-specific performance and thus has the potential to bring new insights into the development of curriculum and instructional design in various countries.

Exploring student performance profiles through the cross-subject analysis requires information on different domains. The present study further investigates if the distributions of performance profiles vary by country, gender, and language at home. Therefore, international large-scale assessments in education provide a valuable data source because it allows discovering variation in the content coverage of curriculum in different countries which could be observed only with international data. Moreover, international assessment studies also collect extensive background information about students.

The combined assessment of the Trends in International Mathematics and Science Study (TIMSS) and the Progress in International Reading Literacy Study (PIRLS) 2011 offers an exceptional opportunity to observe performance in mathematics, reading, and science of fourth graders in several countries. In a set of consecutive studies, Bos, Wendt, Ünlü, Valtin, Euen, Kasper, and Tarelli (2012a, b), Wendt and Kasper (2016), and Bergold, Wendt, Kasper, and Steinmeyr (2017) used the data from TIMSS and PIRLS 2011 to explore the interrelation of academic performances in mathematics, reading, and science among students. It is worth mentioning that factor analysis has established itself as a traditional method in researching individual differences in terms of cognitive abilities, but the above-mentioned studies applied latent profile analysis (LPA) in order to cluster students based on their test scores in mathematics, reading, and science. Using a model with seven performance profiles, the authors found that students varied in their overall performance levels across all subject domains but not in their individual performance profile shape as the profiles appeared to be almost parallel to each other. This finding indicated that students had no specific strength and weaknesses in different academic domains. Further analyses demonstrated that the performance profiles were sensitive to student background characteristics. Thus, boys were overrepresented in high and low performing clusters in comparison to girls, socially disadvantaged students were overrepresented in low performing profiles, while privileged children outnumbered other students in high performance profiles. In regard to cross-national variation, there was a certain heterogeneity of student achievements across subjects, and still it was concluded that for almost all countries involved in the analysis, the identified subject-specific strengths and weaknesses were rather small (Wendt and Kasper 2016).

In contrast to this previous research, we assume in the present study that students do differ in terms of the overall performance as well as in specific strengths and weaknesses. We believe that the lack of evidence for distinct performance profiles in subject-specific strengths and weaknesses in the above-mentioned studies was caused by the analytical approach. The previous studies applied LPA which clusters individuals based on observed variables to classes with different performance profiles. We hypothesise that LPA might be more sensitive to the differences of the overall student performance levels than to the differences in the individual profiles of subject-specific strengths and weaknesses. This hypothesis is formulated on the basis of the two-factor theory of intelligence, suggesting that cognitive abilities are determined by both general and specific intelligences which are intertwined in their nature (cf. Gustafsson and Undheim 1996). Translated to academic achievement, this theory suggests that students should differ in both overall achievement levels but also domain-specific strengths and weaknesses. In our opinion, in order to identify subject-specific strengths and weaknesses, it is essential to control for differences in the general achievement levels by modelling them simultaneously by means of a continuous latent factor. Therefore, the main aim of the present study is to test our hypothesis of both differential achievement levels and between-subject profiles by replacing person-centered LPA with a factor mixture analysis (FMA) to model simultaneously latent continuous and categorical variables. Similarly to the previous research, we use the combined data from TIMSS and PIRLS 2011 in order to test if students have distinct performance profiles of strengths and weaknesses across domains. Furthermore, we compare the distribution of the profiles across countries, across students who do and do not speak the language of test at home, and across boys and girls.

2 Do international assessments measure the same or different academic performances?

International assessments like PIRLS, PISA (Programme for International Student Assessment), and TIMSS administrate different achievement tests to assess academic achievement in various domains. Previous research has revealed high intercorrelations among test scores in different academic domains. Bos et al. (2012b) reported latent correlations between .54 and .74 for the mathematics, reading, and science tests in primary school using German data from the joint administration of PIRLS and TIMSS. Even higher latent correlations between .82 and .89 were reported for the mathematics, reading, and science tests in PISA (OECD, 2001). There is an ongoing debate on whether different tests measure the same or different traits. To understand this discussion, it seems worth to remember that there is a similar debate on cognitive abilities which originates more than 100 years ago. We will briefly review this research before we move to the recent research on the structure of academic achievement measured in international assessments.

In the early 1900s, Spearman (1927) introduced the concept of general intelligence to explain why individuals perform similarly across different cognitive tasks. The idea of a single general ability has been contested among others by Thurstone (1938) who rejected the idea of a single general factor in favour of several and rather independent primary mental abilities like verbal, numerical, or spatial visualization. Further theoretical and empirical research has refined and combined both concepts into unifying models of intelligence which acknowledge that individuals tend to perform similarly across a wide range of cognitive tasks and that the same individuals have particular strengths and weaknesses in more specific cognitive tasks. Although contemporary models of intelligence differ considerably in detail, they acknowledge the existence of both general and specific factors of intelligence (e.g. Carroll 1993; Gustafsson 1984; Härnqvist, Gustafsson, Muthén, and Nelson 1994; Horn and Cattell 1966; Valtin, Kvist and Gustafsson 2008). The conclusions of this long line of argumentation can be translated to the field of academic achievement.

3 Specific learning environments shape specific academic performances

International assessments are designed to measure student performance in academic domains such as mathematics, reading, and science. In comparison to intelligence tests, the tests from international assessments focus on student learning outcomes that are the results of specific learning processes. According to the ecological system theory, individuals are embedded in multiple environments and the development of a person is influenced to a different extent by the interaction with them (Bronfenbrenner 1979). While some of these environments may support learning in general, there are several examples of environments that shape specific academic achievements. For example, countries have different curricula that emphasize certain school subjects, which may manifest in particular strengths or weaknesses in student performance (e.g. Bishop 1997; Schmidt et al. 2001). Another example is culture and societal norms such as gender roles and stereotypes in certain cultures. If female students are, for example, less likely to see their professional future in mathematics or science, this may affect their interests and educational choices which could result in gender-specific strengths or weaknesses in different domains. Previous research on gender gaps in primary school children indicates that in most countries, girls show higher average reading scores than boys, while boys have small mathematics advantages in some and girls in other countries, and gender gaps in science are not significantly different from zero in most countries (Mullis, Martin, Foy, and Hooper 2017; Mullis, Martin, Foy, and Hooper 2016; Mullis, Martin, Foy, and Arora 2012a; Mullis, Martin, Foy, and Drucker 2012b). In older students, more pronounced gender gaps are often reported (OECD 2015). Families are an important learning environment for children. While some family characteristics such as the socioeconomic status may affect learning in different domains simultaneously, other family characteristics like the language of family communication could be more important for learning progress in reading than in mathematics. In this respect, research has shown that students who speak a different language than the language of test at home experience problems due to limited vocabulary or practical language skills. For this reason, the achievement gaps between children who did and did not speak the language of the test before school start tend to be smaller in mathematics than in reading (e.g. Gersten and Woodward 1994; Moss and Puma 1995; Mullis, Martin, Foy, and Arora 2012a; Mullis, Martin, Foy, and Drucker 2012b).

4 Research on the dimensionality of achievement in international assessments

Conventional approaches to examine the associations among achievement scores in different domains assess the dimensionality of assessment data by applying variable-centered factor analytical approaches. Factor analytical approaches identify a set of latent continuous factors that account for individual differences in test data. Bos et al. (2012b) used the combined PIRLS and TIMSS primary school data to compare a confirmatory factor analysis (CFA) model with a single general factor with a model with three correlated factors for mathematics, reading, and science and reported that the multidimensional model had a better fit to the data. Baumert, Lüdtke, Trautwein, and Brunner (2009) used confirmatory factor analysis (CFA) to study the dimensionality of PISA data on performance of 15-year-olds and reported that a model with both general and specific factors for mathematics, reading, and science fitted the data better than a unidimensional model with a single general factor. The authors emphasized that “domain-specific abilities make an incremental contribution to performance, above and beyond g, and have differential validities with key educational student characteristics” (p. 173). Further studies based on international large-scale assessments provided further evidence that test data are best modelled by general and specific factors (e.g. Saß, Kampa, and Köller 2017; Brunner 2005; Nagy 2006; Gustafsson and Balke 1993).

The dimensionality of student achievement in international assessments has not only been studied by means of latent continuous factors but also by modelling latent categorical classes. In contrast to the factor analytical research that showed that international assessments measure a general factor and specific factors, two recent person-centered studies suggest that students do not exhibit strengths and weaknesses in specific academic domains. Wendt and Kasper (2016) and Bergold, Wendt, Kasper, and Steinmayr (2017) used LPA to cluster students based on their mathematics, reading, and science scores from 17 European countries that participated in PIRLS and TIMSS and found out that students differed in the overall performance levels across all domains but not in the profiles of strengths and weaknesses between domains. They identified seven achievement profiles that appeared to be parallel and equidistant. Wendt and Kasper (2016, p. 20) concluded that “achievement across domains can be explained by a general level of achievement rather than subject-specific strengths or weaknesses of learners.”

5 Why does latent profile analysis not replicate the findings of factor analytical studies?

LPA minimizes the within-cluster variation and maximizes the between-cluster variation of the indicator variables (e.g. Vermunt and Magidson 2002). Wendt and Kasper (2016) reported in addition to the within-country variation in performance huge national differences in student achievement. The highest performing countries (e.g. Finland, Northern Ireland) score on average up to more than one standard deviation higher than average students in lower performing countries (e.g. Malta, Romania) in the mathematics, reading, and science tests in PIRLS and TIMSS 2011. For this reason, LPA may simply be more sensitive to the observed huge differences in the overall performance levels than to the differences in the profile shapes of subject-specific strengths and weaknesses.

This interpretation is substantiated by another study that applied LPA to a more homogenous sample of college students in the US. Wang, Eccles, and Kenny (2013) examined mathematics and verbal test scores of twelfth-grade college students and identified five distinct profiles: high mathematics and high verbal scores; high mathematics and moderate verbal scores; moderate mathematics and moderate verbal scores; low mathematics and high verbal scores; and low mathematics and low verbal scores. Hence, their evidence pointed out that there are indeed heterogeneous performance profiles and students differ not only in the general level of achievement across domains but also in specific strengths and weaknesses. It is important to note that Wang and colleagues used data from a highly selective and homogeneous sample of intellectually able students, while Wendt and colleagues used much more heterogeneous international data.

5.1 The present study

Do international assessments measure different specific academic performances or just a single general achievement level? Studies that have employed variable- and person-centered approaches to investigate the dimensionality of international assessments are inconclusive. A number of variable-centered factor analytical studies showed that domain-specific performances make an incremental contribution to performance because the test scores in different academic domains are associated but not perfectly correlated. Imperfect correlations suggest that students tend to perform at the same performance level across domains but at the same time they have strengths and weaknesses in specific domains. In contrast to this finding, person-centered studies that have used LPA identified different profiles that differed only in terms of overall performance levels but not in terms of distinct profile of strengths and weaknesses across domains.

Previous LPA studies failed to take into account that students differ not only in terms of specific strengths and weaknesses but also in their overall performance level. We hypothesise that LPA is more sensitive to differences in the overall performance level than to differences in the profile shapes, and, therefore, the main aim of the present study is to test whether students have distinct performance profiles of subject-specific strengths and weaknesses when also controlling for differences in the overall achievement levels. For this purpose, we use factor mixture analysis (FMA) to combine continuous and categorical latent variables when modelling PIRLS and TIMSS test scores in mathematics, reading, and science. The flat profiles that were identified in previous research (see Wendt and Kasper 2016; Bergold, Wendt, Kasper, and Steinmayr 2017) imply only mean achievement differences and no subject-specific strengths or weaknesses. This would imply that subject-specific learning environments do not matter and that the sole predictor of achievement in a subject would be the overall achievement level of a student. We used Bronfenbrenner’s theory to challenge this assumption, since differential learning environments (e.g. different teachers in mathematics and reading, different curricula) can be expected to matter. If the conclusions from previous studies would be true, our FMA would have revealed only one latent class with a flat profile in all countries, after accounting for general achievement level differences in a latent factor. We tested this assumption by using a pooled international dataset. Another advantage of using the pooled international dataset is that the large sample size allows identifying comparably small latent classes. Our FMA that based on the international dataset revealed that a large share but not all students showed about the same performance in reading, mathematics, and science, which contradicted the previous studies. In order to validate our FMA results, we further investigated if the relative subject-specific strengths and weaknesses conformed with theoretical assumptions. We argued that following previous literature, girls should be more likely than boys to show relative strengths in reading (and vice versa in mathematics) and non-native students should have relative weaknesses in reading after controlling for overall achievement levels. Also, countries should differ in the profile proportions due to curricula differences.

Specifically, we will model one continuous latent factor to capture differences in the overall achievement levels. In addition, we test if students have strengths and weaknesses in specific domains by modelling latent classes that are defined by different intercepts in mathematics, reading, and science. To validate our analyses, we will compare the FMA models with conventional CFA and LPA models. We will further investigate (1) if boys and girls differ in academic strengths and weaknesses, (2) if students who always, sometimes, or never speak the language of test at home differ in their domain-specific strengths and weaknesses, and (3) if countries show differences in their proportions of students with certain strengths and weaknesses. Thus, such student background variables as gender, use of the language of test at home, and country were selected for the analysis because they are widely discussed in the previous literature on student performance and in particular on subject-specific strengths and weaknesses (Wendt and Kasper 2016; Bergold, Wendt, Kasper, and Steinmayr 2017; Mullis, Martin, Foy, and Hooper 2017; Mullis, Martin, Foy, and Hooper 2016; Mullis, Martin, Foy, and Arora 2012a; Mullis, Martin, Foy, and Drucker 2012b; Gersten and Woodward 1994; Moss and Puma 1995) which makes our findings comparable with the previous results in this field. It should be noted that the primary aim of the present study is to explore the subject-specific strengths and weaknesses, and the covariates such as gender, language background, and country are used in the analysis for validation purpose. This is beyond the scope of the present study to explain variation of the performance profiles depending on the covariates, but rather the study provides ground for further investigation of why the distribution of the performance profiles vary based on gender, language background, and country.

6 Method

6.1 Sample

We used the combined data from TIMSS and PIRLS that were administered to the same student samples in 35 countries or regions in 2011. All countries are listed in Table 1. The total sample contains N = 177,480 fourth graders. The sampling procedures of TIMSS and PIRLS ensure the comparability of students based on their age and amount of schooling.Footnote 1 All participating countries and regions adopted a rigorous sampling framework to generalize the analyses to the national respectively regional populations of fourth graders. In the main analyses, we used a pooled sample of all students in all countries. We ran all models and applied senate weights (SENWGT) so that all countries contribute equally to the findings.

Table 1 Number of students, number of girls and boys, mean scores in mathematics, science, and reading, and number of students who always, sometimes, and never speak the language of test at home in the investigated countries and regions
Full size table

6.2 Measures

6.2.1 Achievement scores

The main achievement variables are the mathematics, reading, and science plausible values from TIMSS and PIRLS 2011. PIRLS 2011 measured students’ proficiency in reading based on 135 items. The TIMSS 2011 test on mathematics comprised 175 items, and the science component contained 172 items. The tests were designed based on a curriculum that was comparable for all participating countries (Mullis, Martin, Kennedy, Trong, and Sainsbury 2009a; Mullis, Martin, Ruddock, O'Sullivan, and Preuschoff 2009b). All five plausible values were used in this analysis. The test scores in each domain have an international mean of 500 with a standard deviation of 100 (based on the first administration of PIRLS in 2001 and TIMSS in 1995). Table 1 shows considerable variation in the mean performance across countries. We divided the achievement scores by 100 to ease the estimation of the models in Mplus. Therefore, in the analyses, the scores were on a scale with a mean of 5 and a standard deviation of 1.

6.2.2 Covariates

As a further validation, we compared the distribution of the identified performance profiles based on the three covariates: country, gender, and language at home. The total sample contains 86,807 girls and 89,665 boys. Students were asked how often they speak the test language at home: 114,111 students reported always or almost always; 43,605 spoke sometimes the language of test, and 10,786 never used it at home. Overall, 8978 students did not answer this question. The missing value rates of the covariates gender (0.01%) and language at home (0.05%) were close to zero. We excluded cases with missing covariate information from the respective validation analyses. The distribution of classes varies slightly by covariates because the covariates have different rates of missingness. The country sample sizes, the distribution of gender, and the language at home are presented in Table 1.

7 Analyses

7.1 Factor mixture, latent profile, and confirmatory factor analyses

We used latent continuous and latent categorical variable modelling to investigate the dimensionality of the test scores in mathematics, reading, and science using the combined data from the 35 countries and regions that participated in TIMSS and PIRLS 2011.

Our main models are constrained FMA models that combine latent continuous and categorical variables to reveal strengths and weaknesses in specific academic domains while controlling for differences in the overall performance level. For this purpose, we specified FMA models with one latent factor—measured by the three achievement scores in mathematics, reading, and science—to account for continuous differences in the general performance levels across domains. In addition, we specified latent classes—measured by different intercepts for mathematics, reading, and science subscores—to model subject-specific strengths and weaknesses. We specified six FMA candidate models that all contain one latent factor and between one to six latent classes. We included some model constraints to identify the models. The sums of the three intercepts were constrained to be equal across the classes because we aimed to capture differences in the overall performance levels by the latent factor as well as differences in the profiles of strengths and weaknesses across domains by the latent classes. The residual variances were constrained to be equal across classes.

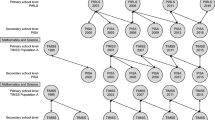
We compared the FMA models with conventional CFA and LPA models. We estimated a series of LPA models with up to eight latent classes. The difference between the FMA and the LPA models is that the LPA models do not contain a latent continuous factor. The main drawback of such a model is that it fails to capture general differences in the performance levels across domains. For this reason, it is difficult to disentangle differences in the general performance levels across domains from specific strengths and weaknesses in mathematics, reading, and science. Furthermore, we specified a simple CFA model where we modelled the covariance between the three test scores with a single latent factor. It is not possible to estimate more complex multidimensional CFA models with only three manifest variables because they are not identified. The CFA model with a single latent factor is equivalent to an FMA model with one single class. The FMA, CFA, and LPA models are depicted in Fig. 1, where the latent factor f is supposed to capture variation in the general performance level and the latent profile variable c models the subject-specific strengths and weaknesses. For the analyses of this study, we used Mplus (Muthén & Muthén, 1998-2017).

Fig. 1
figure 1

The analytical models

Full size image

7.2 Model comparisons

An important step in latent variable modelling is to decide upon the best fitting and most parsimonious model. As we did not have compelling reasons to decide on a model with a particular number of performance profiles in advance, we estimated different candidate models. There is no single method for comparing FMA, LPA, and CFA models that is widely accepted as best. Our selection among these models was driven by both empirical and substantive considerations. For all models, we recorded the Bayesian information criterion (BIC), the entropy, and the proportion of students in the smallest class. The BIC is likelihood-based with a penalty for model complexity and smaller values indicating better model fit (Schwarz 1978). The entropy quantifies the precision with which each student can be placed into latent classes or profiles (Ramaswamy, Desarbo, Reibstein, and Robinson 1993). The proportion of students in the classes was recorded because a very small class rather indicates an over-extraction of classes than a class with substantive meaning (Masyn, Henderson, and Greenbaum 2010).

7.3 Analyses with covariates

The next step in our analyses of performance profiles was to investigate the distribution of the performance profiles across the covariates. For this purpose, we used the estimated model parameters of the FMA model as fixed parameters and assigned each student to their most likely latent profile based on the first plausible values. We compared the distribution of the performance profiles across countries, gender, and between students of different language backgrounds.

8 Results

8.1 Model selection

For the LPA models, one to eight latent classes were specified; for the CFA, one model with a single latent factor; and for the FMA models, two to six latent profiles and one latent factor. Table 2 displays the fit indices for all estimated models. The BIC suggests that the FMA models fit the data better than the LPA and CFA models. The entropy, which is only available for models with latent classes, is roughly the same across all estimated LPA and FMA models and, thus, does not provide much guidance for the model selection. For this reason, we conclude that the FMA is the more suitable approach to model the latent structure of the test scores than LPA and CFA.

Table 2 Fit indices for candidate models. The CFA model and an FMA model with one single class are equivalent. Examples of the Mplus syntaxes of the 3-class LPA, the CFA, and the 3-class FMA are depicted in the Appendix 1 and full model results in Appendix 2
Full size table

We next compared the five estimated FMA candidate models. The BIC decreases constantly for the models with additional latent classes but the gains in model fit decreases with model complexity. The difference between the BICs of FMA models with two and three latent classes is roughly 7400 but only 2700 for the comparison of the models with three and four as well as four and five classes. Additionally, the FMA models with four or more classes resulted in very small classes that represent only 2 or less percent of the students. This suggests that the three-class FMA model provides a more parsimonious way of describing the latent structure and that the added value of estimating additional classes is small. For this reason, we can make the tentative conclusion that the latent profiles in student achievement, as measured by the PIRLS and TIMSS tests, derive from the three latent subpopulations. We will next describe this model in detail.

8.2 Model interpretation

The generated FMA with one latent factor and three latent classes revealed distinct performance profiles of students. The main finding is that the shapes of the profiles differ which supports the assumption that students do have different strengths and weaknesses across subject domains. The performance profiles in Fig. 2 show that one class of students is characterized by a relative strength in mathematics, medium performance in science, and a relative weakness in reading (Profile 1), a second class scores high in mathematics and reading, but comparably low in science (Profile 2), and a third class of students has a mostly flat profile without pronounced strengths or weaknesses in mathematics, reading, or science (Profile 3). The differences between the three domains are statistically significant for all classes except for the difference between reading and science in Profile 3. We observe an uneven distribution of students across the three classes based on the estimated model (Profile 1: 10.45%; Profile 2: 3.48%; Profile 3: 86.07%) and the most likely class membership (Profile 1: 8.20%; Profile 2: 2.60%; Profile 3: 89.10%).

Fig. 2
figure 2

Performance profiles of the FMA model with one factor and three classes. Presented are relative frequencies of students in the respective profiles based on the most likely class membership

Full size image

8.3 Covariate analyses

In the following, we explore the distribution of the performance profiles across countries, gender, and the language students speak at home. The quality of the classification as measured by the entropy is .87 which we consider sufficiently high to use the most likely class membership as a variable in further analyses. We hypothesise that the relative profile frequency should vary across countries, gender, and the language spoken at home. Note that the distributions of classes in Fig. 3 and Fig. 4 differ slightly because the gender and language covariates have small amounts of missing data.

Fig. 3
figure 3

Differences in performance profiles by language at home. Presented are relative frequencies of students in the respective profiles based on the most likely class membership

Full size image
Fig. 4
figure 4

Differences in performance profiles by gender. Presented are relative frequencies of students in the respective profiles based on the most likely class membership

Full size image

8.3.1 Language at home

Figure 3 illustrates the distribution of the performance profiles within different groups of language backgrounds. The share of students in the profile that performed relatively low in reading (Profile 1) increases with the decrease of the use of the test language at home. About one third of the students, who reported that they never speak the test language at home, were assigned to Profile 1 with a relative weakness in reading. At the same time, only 7.63% of students who reported that they always or almost always speak the test language at home exhibited a relatively low performance in reading and were assigned to Profile 1. In contrast, students who never use the test language at home did particularly well in mathematics as they are overrepresented in Profile 2. About 12% of the total sample of students in this group were assigned to Profile 2. Most students across all language backgrounds belong to Profile 3 that reflects a balanced performance across the three subject domains.

8.3.2 Gender

Another covariate of interest was gender. Our results show that boys are slightly overrepresented in Profile 1 with a strength in mathematics and weakness in reading, while girls are somewhat overrepresented in Profile 3 with a balanced performance across domains (Fig. 4). We observed hardly any gender differences in the relative frequency of the Profile 2, the performance profile with a relative strength in mathematics and reading and relative weakness in science.

8.3.3 Countries

Figure 5 provides compelling evidence for cross-country differences in the relative profile frequencies, i.e. how well students perform in different domains. In some countries, almost all students were assigned to the Profile 3 with the balanced performance levels across all three domains (e.g. Austria, Spain, Oman, Taiwan) but in other countries/regions like Abu Dhabi, Iran, Italy, Ireland, and Northern Ireland, a rather large share of students show a particular strength in mathematics coupled with pronounced weakness in reading (Profile 1) or science (Profile 2).

Fig. 5
figure 5

Differences in performance profiles by country. Presented are relative frequencies of students in the respective profiles based on the most likely class membership

Full size image

9 Discussion

In the present study, we examined the subject-specific strengths and weaknesses in mathematics, reading, and science among fourth graders worldwide. We achieved this by combining latent continuous and categorical variables to explore the dimensionality of test scores. Specifically, we used FMA to model one continuous latent factor that captured the overall differences in performances and latent classes with varying mathematics, reading, and science intercepts that captured distinct performance profiles of students. Our findings indicate that FMA achieves a better fit for the data than CFA and LPA when analysing subject-specific strengths and weaknesses. The whole sample from TIMSS and PIRLS 2011 was assigned to the estimated performance profiles that indicated subject-specific strengths and weaknesses. Furthermore, we investigated the distribution of performance profiles across different subgroups that we assumed to show different strengths and weaknesses across the domains. Specifically, we explored the performance profile distributions across countries, student gender, and language of communication at home. We found cross-country differences in the subject-specific strengths and weaknesses. This can be interpreted as an indication for differences in national curricula that affect the development of subject-specific strengths and weaknesses among students. The results of the study also indicate that there are slight differences in subject-specific strengths and weaknesses among girls and boys because there are more boys assigned to Profile 1 with relatively high performance in mathematics but lower performance in reading. Furthermore, the analysis showed that subject-specific strengths and weaknesses are associated with the language of communication at home as many students who do not speak the language of test at home exhibited relative weakness in reading and at the same time possessed relative strengths in mathematics. The validation analyses supported that our FMA did not identify spurious classes (Bauer and Curran 2004) but substantively meaningful differences between the students. However, we leave more detailed analyses of specific strengths and weaknesses between countries to future research, which should then indeed specify separate models for the countries and conduct a more thorough comparison.

The rationale behind using the TIMSS and PIRLS 2011 combined dataset is that it assesses curriculum-based competencies and is hence more oriented towards subject domains at school. In contrast, another large-scale assessment PISA evaluates general literacy and student competencies that are required for successful participation in society; PISA also emphasizes only one subject domain per cycle which implies that there are substantially fewer test items in the other domains to be tested. The TIMSS and PIRLS data of the cycle 2011 provides a unique opportunity to study all three domains which coincide in time. Finally, analysing subject-specific strengths and weaknesses based on TIMSS and PIRLS 2011 allows for comparison with the previous studies on subject-specific performance of students that used the same data (e.g. Wendt and Kasper 2016; Bergold, Wendt, Kasper, and Steinmayr 2017).

9.1 Profile dynamics

The key finding of our study is that while most students show about the same performance level across mathematics, reading, and science, a share of students does differ in the profiles of subject-specific strengths and weaknesses across domains. We ran various FMA models and further analysed in detail a model with three profiles that showed divergent dynamics across subject domains. The differences in the shapes of the profiles support our hypothesis that some students possess specific strengths and weaknesses in subject domains. This finding significantly differs from previous results reported in the literature which suggested that students do not exhibit any academic strengths or weaknesses but rather have well-balanced performances in mathematics, reading, and science (e.g. Wendt and Kasper 2016; Bergold, Wendt, Kasper, and Steinmayr 2017). In contrast, our results revealed differences in student performance across domains for two subpopulations of students (Profiles 1 and 2) and at the same time we also find a subpopulation with a well-balanced performance profile (Profile 3) that reflects about the same scores in all three domains.

Thus, a possible explanation for the fact that earlier studies did not find relative strengths and weaknesses in student academic performance may be due to the analytical approach that they applied. For instance, Wendt and Kasper (2016) as well as Bergold, Wendt, Kasper, and Steinmayr (2017) used the LPA approach to model performance profiles. Our FMA showed a better fit model in comparison with the LPA. This leads to the conclusion that the FMA is a more appropriate methodological approach for analysing subject-specific strengths and weaknesses among students. We also argue that LPA might be more sensitive to overall differences in the performance levels rather than to the differences in the profile shapes. Our approach to explore differences in the shapes of profiles of subject-specific strengths and weaknesses is to also model differences in performance levels by combining continuous and categorical latent variables in an FMA framework.

Our results share a number of similarities with previous research findings. Across countries, our study indicates that in comparison to girls, boys were slightly overrepresented in Profile 1, in which children exhibit relative strengths in mathematics and relative weaknesses in reading, regardless of their overall performance level across the domains. Girls were slightly overrepresented in Profile 3, the profile with the balanced performances in all three domains. Furthermore, our analyses indicate that children who did not or only sometimes spoke the language of test at home were relatively overrepresented in the Profiles 1 and 2, i.e. the profiles with relative weaknesses in reading and science in comparison to mathematics. Our interpretation of this finding refers to the fact that both learning processes in reading and primary school science might be more challenging for non-native speaking students since it requires extracurricular reading activities. An interesting finding of our study is the striking differences across countries. Some countries have a large share of students with profiles that indicate relative strengths in mathematics, while other countries have a high share of students that show relative strengths in reading. This finding points to the importance of national curricula in shaping student performance in different domains. The fact that the profile distributions varied by country, gender, and language at home supports the latent profiles that were identified in the three-class FMA.

9.2 Limitations and future directions

It seems worth to stress some limitations of our research. First, we focus on the end of primary school and the observed differences in profiles may be even larger in secondary school. Second, we examined student achievement only in mathematics, science, and reading. Although these three domains are considered to be core academic areas that can predict further life outcomes of students, there are also other important domains that could be included in the analysis, for example digital literacy or civic knowledge. Third, we used the combined data from 35 countries to fit a set of latent class, latent factor, and factor mixture models. Analyses of the data from individual countries may result in different results. Indeed, there is some evidence that it is possible to improve the model fit by extracting further latent classes. However, we observed that even for the FMA model with three latent classes, one profile was hardly represented in some countries. Still, further research may explore and study further performance profiles.

10 Conclusions

The evidence from this study suggests that methods matter in the analysis of academic strengths and weaknesses among students. As Maslow (2002) put it: “it is tempting, if the only tool you have is a hammer, to treat everything as if it were a nail” (p. 15). While previous research using the combined PIRLS and TIMSS data concluded that “profiles differed only in […] overall performance level across all academic competencies” (Bergold et al. 2017, p. 439), we have demonstrated that it is possible to identify differences in the profiles of subject-specific strengths and weaknesses. The identification of such distinct performance profiles requires an analytical strategy that is sensitive to differences in overall performance levels. Our study suggests that the approach to control for variation in the overall achievement levels from test scores in different domains is a promising approach to identify distinct performance profiles across academic achievement domains.

Thus, our study contributed to the debate on scholastic performance of students: By dwelling on the theory of general and specific factors of intelligence, we demonstrated that students possess subject-specific strengths and weaknesses and at the same time there are students whose scholastic performance is similar across subject domains. The results of the study reveal that TIMSS and PIRLS assess not only the general performance of students but also their subject-specific strengths and weaknesses. Hence, the study provides ground for further investigations of the factors that influence subject-specific performance. Specifically, we suggest focusing on educational policy and national curricula differences that shape the countries’ average subject-specific strengths and weaknesses of students. Finally, our study contributed to the field of applied methodological research as our analysis demonstrated that methods matter in analysing student performance. We showed that FMA is a more appropriate approach to unveil subject-specific strengths and weaknesses than LPA, which does not account for differences in overall achievement.