Skip to main content
SpringerLink
Log in

Quasiplanar Diagrams and Slim Semimodular Lattices

  • Published:
Order Aims and scope Submit manuscript

Abstract

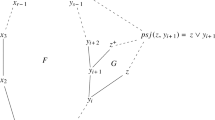
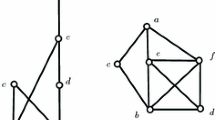
For elements x and y in the (Hasse) diagram D of a finite bounded poset P, x is on the left of y, written as x λ y, if x and y are incomparable and x is on the left of all maximal chains through y. Being on the right, written as x ϱ y, is defined analogously. The diagram D is quasiplanar if λ and ϱ are transitive and for any pair (x,y) of incomparable elements, if x is on the left of some maximal chain through y, then x λ y. A planar diagram is quasiplanar, and P has a quasiplanar diagram iff its order dimension is at most 2. We are interested in diagrams only up to similarity. A finite lattice is slim if it is join-generated by the union of two chains. The main result gives a bijection between the set of (the similarity classes of) finite quasiplanar diagrams and that of (the similarity classes of) planar diagrams of finite slim semimodular lattices. This bijection allows one to describe finite posets of order dimension at most 2 by finite slim semimodular lattices, and conversely. As a corollary, we obtain that there are exactly (n−2)! quasiplanar diagrams of size n.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abels, H.: The geometry of the chamber system of a semimodular lattice. Order 8, 143–158 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  2. Adaricheva, K.: Representing finite convex geometries by relatively convex sets. Eur. J. Comb. 37, 68–78 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  3. Adaricheva, K., Czédli, G.: Notes on the description of join-distributive lattices by permutations. Algebra Univers. 72, 155–162 (2014)

    Article  MATH  Google Scholar 

  4. Adaricheva, K., Gorbunov, V.A., Tumanov, V.I.: Join-semidistributive lattices and convex geometries. Adv. Math. 173, 1–49 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  5. Armstrong, D.: The sorting order on a Coxeter Group. J. Comb. Theory Ser. A 116, 1285–1305 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  6. Avann, S.P.: Application of the join-irreducible excess function to semimodular lattices. Math. Ann. 142, 345–354 (1961)

    Article  MathSciNet  MATH  Google Scholar 

  7. Caspard, N., Monjardet, B.: Some lattices of closure systems on a finite set. Discrete Math. Theor. Comput. Sci. 6, 163–190 (2004)

    MathSciNet  MATH  Google Scholar 

  8. Czédli, G.: The matrix of a slim semimodular lattice. Order 29, 85–103 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  9. Czédli, G.: Representing homomorphisms of distributive lattices as restrictions of congruences of rectangular lattices. Algebra Universalis 67, 313–345 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  10. Czédli, G.: Coordinatization of join-distributive lattices. Algebra Universalis 71, 385–404 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  11. Czédli, G.: Finite convex geometries of circles. Discrete Math. 330, 61–75 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  12. Czédli, G.: The asymptotic number of planar, slim, semimodular lattice diagrams. Order. (2015). doi:10.1007/s11083-015-9361-0

  13. Czédli, G., Dékány, T., Ozsvárt, L., Szakács, N., Udvari, B. On the number of slim, semimodular lattices. Mathematica Slovaca, to appear; arXiv:1208.6173

  14. Czédli, G., Grätzer, G.: Notes on planar semimodular lattices. VII. Resections of planar semimodular lattices. Order 30, 847–858 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  15. Czédli, G., Grätzer, G.: Planar semimodular lattices and their diagrams. Chapter 3. In: Grätzer, G., Wehrung, F (eds.) Lattice Theory: Special Topics and Applications. Basel, Birkhäuser Verlag (2014)

  16. Czédli, G., Ozsvárt, L., Udvari, B.: How many ways can two composition series intersect? Discrete Math. 312, 3523–3536 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  17. Czédli, G., Schmidt, E.T.: The Jordan-Hölder theorem with uniqueness for groups and semimodular lattices. Algebra Universalis 66, 69–79 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  18. Czédli, G., Schmidt, E.T.: Slim semimodular lattices. I. A visual approach. Order 29, 481–497 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  19. Czédli, G., Schmidt, E.T.: Composition series in groups and the structure of slim semimodular lattices. Acta Sci. Math. (Szeged) 79, 369–390 (2013)

    MathSciNet  MATH  Google Scholar 

  20. Czédli, G., Schmidt, E.T.: Slim semimodular lattices. II. A description by patchwork systems. Order 30, 689–721 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  21. Dilworth, R.P.: Lattices with unique irreducible decompositions. Ann. Math. 41 (2), 771–777 (1940)

    Article  MathSciNet  MATH  Google Scholar 

  22. Grätzer, G.: Lattice Theory: Foundation. Basel, Birkhäuser Verlag (2011)

    Book  MATH  Google Scholar 

  23. Grätzer, G., Knapp, E.: Notes on planar semimodular lattices. I. Construction. Acta Sci. Math. (Szeged) 73, 445–462 (2007)

    MathSciNet  MATH  Google Scholar 

  24. Grätzer, G., Knapp, E.: Notes on planar semimodular lattices. III. Congruences of rectangular lattices. Acta Sci. Math. (Szeged) 75, 29–48 (2009)

    MathSciNet  MATH  Google Scholar 

  25. Grätzer, G., Knapp, E.: Notes on planar semimodular lattices. IV. The size of a minimal congruence lattice representation with rectangular lattices. Acta Sci. Math. (Szeged) 76, 3–26 (2010)

    MathSciNet  MATH  Google Scholar 

  26. Jamison-Waldner, R.E.: Copoints in antimatroids. In: Combinatorics, graph theory and computing. Proc. 11th southeast. Conf., Boca Raton/Florida 1980, Vol. II, Congr. Numerantium vol. 29, pp. 535–544 (1980)

  27. Kelly, D., Rival, I.: Planar lattices. Canad. J. Math. 27, 636–665 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  28. Monjardet, B.: A use for frequently rediscovering a concept. Order 1, 415–417 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  29. Nation, J.B.: Notes on Lattice Theory. http://www.math.hawaii.edu/~jb/books.html

  30. Schmidt, E.T.: Congruence lattices and cover preserving embeddings of finite length semimodular lattices. Acta Sci. Math. Szeged 77, 47–52 (2011)

    MathSciNet  MATH  Google Scholar 

  31. Stern, M.: Semimodular Lattices. Theory and Applications, Encyclopedia of Mathematics and its Applications 73. Cambridge University Press, Cambridge (1999)

    Book  Google Scholar 

  32. Ward, M.: Structure residuation. Ann. Math. 39(2), 558–568 (1938)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Szeged, Bolyai Institute, Aradi vértanúk tere 1, 6720, Szeged, Hungary

    Gábor Czédli

Authors
  1. Gábor Czédli
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Gábor Czédli.

Additional information

This research was supported by the NFSR of Hungary (OTKA), grant numbers K77432 and K83219

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Czédli, G. Quasiplanar Diagrams and Slim Semimodular Lattices. Order 33, 239–262 (2016). https://doi.org/10.1007/s11083-015-9362-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11083-015-9362-z

Keywords

Search

Navigation