Skip to main content
SpringerLink
Log in

New solitary wave solutions to Biswas–Milovic and resonant nonlinear Schrödinger equations

  • Published:
Optical and Quantum Electronics Aims and scope Submit manuscript

Abstract

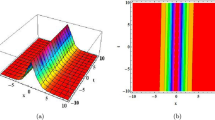
This paper explore the new solitary wave solutions of the Biswas–Milovic equation and resonant nonlinear Schr\(\ddot{o}\)dinger equations with Kerr–Law nonlinearity. In mathematical physics, the Biswas–Milovic equation plays an important role. The dynamics of these solitons are well known to propagate over large distances in a few femto-seconds through these fibres. These dynamics are governed by the nonlinear Schrödinger’s equation. The resonant nonlinear Schrödinger equation can be used to model the propagation of waves in fiber optics. The powerful analytical approach known as the extended simple equation method is employed to explore the solitary wave solutions of the Biswas–Milovic and resonant nonlinear Schr\(\ddot{o}\)dinger equations. These equations are primarily explored in the realm of solitons in nonlinear fiber optics. New dark, kink, anti-kink and singular periodic solitons are secured. Furthermore, 3D surface graphs, contour plots and parametric graphs are drawn to show dynamical behavior of some obtained solutions with the aid of symbolic software such as Mathematica. The constructed solutions will helpful to understand the dynamical framework of nonlinear Schr\(\ddot{o}\)dinger equations in the related physical phenomena.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Data availability statement

Data will be provided on request to the corresponding author.

References

  • Akinyemi, L., Mirzazadeh, M., Hosseini, K.: Solitons and other solutions of perturbed nonlinear Biswas–Milovic equation with Kudryashov’s law of refractive index. Nonlinear Anal. Model. Control 27(3), 479–495 (2022)

    MathSciNet  Google Scholar 

  • Akram, G., Sadaf, M., Khan, M.A.U.: Soliton solutions of the resonant nonlinear Schr\(\ddot{o}\)dinger equation using modified auxiliary equation method with three different nonlinearities. Math. Comput. Simul. 206, 1–20 (2023)

    Article  Google Scholar 

  • Albayrak, P.: Optical solitons of Biswas–Milovic model having spatio-temporal dispersion and parabolic law via a couple of Kudryashov’s schemes. Optik 279, 170761 (2023)

    Article  ADS  Google Scholar 

  • Arnous, A.H., Mirzazadeh, M., Zhou, Q., Mahmood, M.F., Biswas, A., Belic, M.: Optical solitons with resonant nonlinear Schr\(\ddot{o}\)dinger’s equation using G\(^{\prime }\)/G-expansion scheme. Optoelectron. Adv. Mater. Rapid Commun. 9(9–10), 1214–1220 (2013)

    Google Scholar 

  • Asghari, Y., Eslami, M., Rezazadeh, H.: Soliton solutions for the time-fractional nonlinear differential–difference equation with conformable derivatives in the ferroelectric materials. Opt. Quantum Electron. 55(4), 289 (2023a)

    Article  Google Scholar 

  • Asghari, Y., Eslami, M., Rezazadeh, H.: Novel optical solitons for the Ablowitz–Ladik lattice equation with conformable derivatives in the optical fibers. Opt. Quantum Electron. 55(10), 930 (2023b)

    Article  Google Scholar 

  • Asghari, Y., Eslami, M., Rezazadeh, H.: Exact solutions to the conformable time-fractional discretized mKdv lattice system using the fractional transformation method. Opt. Quantum Electron. 55(4), 318 (2023c)

    Article  Google Scholar 

  • Bilige, S., Chaolu, T.: An extended simplest equation method and its application to several forms of the fifth-order KdV equation. Appl. Math. Comput. 216(11), 3146–3153 (2010)

    MathSciNet  Google Scholar 

  • Biswas, A., Milovic, D.: Bright and dark solitons of the generalized nonlinear Schr\(\ddot{o}\)dinger’s equation. Commun. Nonlinear Sci. Numer. Simul 15(6), 1473–1484 (2010)

    Article  ADS  MathSciNet  Google Scholar 

  • Eslami, M., Rezazadeh, H.: The first integral method for Wu–Zhang system with conformable time-fractional derivative. Calcolo 53, 475–485 (2016)

    Article  MathSciNet  Google Scholar 

  • Helal, M.A., Seadawy, A.R.: Exact soliton solutions of a D-dimensional nonlinear Schr\(\ddot{o}\)dinger equation with damping and diffusive terms. Z. Angew. Math. Phys. 62, 839–847 (2011)

    Article  MathSciNet  Google Scholar 

  • Jafari, H., Sooraki, A., Khalique, C.M.: Dark solitons of the Biswas–Milovic equation by the first integral method. Optik 124(19), 3929–3932 (2013)

    Article  ADS  Google Scholar 

  • Lu, D., Seadawy, A., Arshad, M.: Applications of extended simple equation method on unstable nonlinear Schr\(\ddot{o}\)dinger equations. Optik 140, 136–144 (2017)

    Article  ADS  Google Scholar 

  • Manafian, J., Lakestani, M.: Optical solitons with Biswas-Milovic equation for Kerr law nonlinearity. Eur. Phys. J. Plus 130, 1–12 (2015)

    Article  Google Scholar 

  • Mathanaranjan, T.: An effective technique for the conformable space-time fractional cubic-quartic nonlinear Schrodinger equation with different laws of nonlinearity. Comput. Methods Differ. Equ. 10(3), 701–715 (2022a)

    MathSciNet  Google Scholar 

  • Mathanaranjan, T., Kumar, D., Rezazadeh, H., Akinyemi, L.: Optical solitons in metamaterials with third and fourth order dispersions. Opt. Quantum Electron. 54(5), 271 (2022b)

    Article  Google Scholar 

  • Mathanaranjan, T., Hashemi, M.S., Rezazadeh, H., Akinyemi, L., Bekir, A.: Chirped optical solitons and stability analysis of the nonlinear Schrodinger equation with nonlinear chromatic dispersion. Commun. Theor. Phys. 75(8), 085005 (2023)

    Article  ADS  MathSciNet  Google Scholar 

  • Mirzazadeh, M., Arnous, A.H.: Exact solution of Biswas–Milovic equation using new efficient method. Electron. J. Math. Anal. Appl 3, 139–146 (2015)

    MathSciNet  Google Scholar 

  • Nofal, T.A.: Simple equation method for nonlinear partial differential equations and its applications. J. Egypt. Math. Soc. 24(2), 204–209 (2016)

    Article  MathSciNet  Google Scholar 

  • Ozisik, M.: Novel (2+ 1) and (3+ 1) forms of the Biswas–Milovic equation and optical soliton solutions via two efficient techniques. Optik 269, 169798 (2022)

    Article  ADS  Google Scholar 

  • Raza, N., Abdullah, M., Butt, A.R.: Analytical soliton solutions of Biswas–Milovic equation in Kerr and non-Kerr law media. Optik 157, 993–1002 (2018)

    Article  ADS  Google Scholar 

  • Rehman, H.U., Awan, A.U., Tag-ElDin, E.M., Bashir, U., Allahyani, S.A.: Construction of exact solutions for Gilson–Pickering model using two different approaches. Universe 8(11), 592 (2022)

    Article  ADS  Google Scholar 

  • Seadawy, A.R., Wang, J.: Three-dimensional nonlinear extended Zakharov–Kuznetsov dynamical equation in a magnetized dusty plasma via acoustic solitary wave solutions. Braz. J. Phys. 49, 67–78 (2019)

    Article  ADS  Google Scholar 

  • Seadawy, A.R., Ali, A., Zahed, H., Baleanu, D.: The Klein–Fock–Gordon and Tzitzeica dynamical equations with advanced analytical wave solutions. Res. Phys. 19, 103565 (2020)

    Google Scholar 

  • Vahidi, J., Zabihi, A., Rezazadeh, H., Ansari, R.: New extended direct algebraic method for the resonant nonlinear Schr\(\ddot{o}\)dinger equation with Kerr law nonlinearity. Optik 227, 165936 (2021)

    Article  ADS  Google Scholar 

  • Xu, F.: A generalized soliton solution of the Konopelchenko–Dubrovsky equation using He’s exp-function method. Z. Nat. A 62(12), 685–688 (2007)

    Google Scholar 

  • Zhang, S., Xia, T.C.: A generalized auxiliary equation method and its application to (2 + 1)-dimensional asymmetric Nizhnik–Novikov–Vesselov equations. J. Phys. A Math. Theor. 40(2), 227 (2006)

    Article  ADS  MathSciNet  Google Scholar 

  • Zhao, Y.H., Mathanaranjan, T., Rezazadeh, H., Akinyemi, L., Inc, M.: New solitary wave solutions and stability analysis for the generalized (3+ 1)-dimensional nonlinear wave equation in liquid with gas bubbles. Res. Phys. 43, 106083 (2022)

    Google Scholar 

Download references

Acknowledgements

The Authors extend their appreciation to the Deanship Scientific Research at King Khalid University for funding this work through large group Research Project under grant number: RGP2/422/44.

Funding

This research work was supported by the Deanship of Scientific Research at King Khalid University under grant number: RGP2/422/44.

Author information

Authors and Affiliations

  1. Division of Science and Technology, Department of Mathematics, University of Education, Lahore, Pakistan

    Wardat us Salam & Robina Rafeeq

  2. Department of Mathematics, GC Women University, Sialkot, Pakistan

    Hira Tariq

  3. Near East University, Operational Research Center in Healthcare, TRNC Mersin 10, Nicosia, 99138, Turkey

    Hijaz Ahmad

  4. Civil Engineering Department, College of Engineering, King Khalid University, Abha, Saudi Arabia

    Khaled Mohamed Khedher

  5. Department of Mathematics and Informatics, Azerbaijan University, Jeyhun Hajibeyli street, 71, AZ1007, Baku, Azerbaijan

    Hijaz Ahmad

  6. Department of Computer Science and Mathematics, Lebanese American University, Beirut, Lebanon

    Hijaz Ahmad

  7. Department of Mathematics, Faculty of Science, Islamic University of Madinah, Madinah, Saudi Arabia

    Hijaz Ahmad

Authors
  1. Wardat us Salam
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hira Tariq
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Robina Rafeeq
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hijaz Ahmad
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Khaled Mohamed Khedher
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Conceptualization: WS, data curation: RR, formal analysis: HT, validation: HT, writing—original draft: WS, writing—review editing: HA.

Corresponding author

Correspondence to Hijaz Ahmad.

Ethics declarations

Conflict of interest

Authors declare no conflict of interest.

Ethical approval

All the authors demonstrating that they have adhered to the accepted ethical standards of a genuine research study.

Consent to participate

Being the corresponding author, I have consent to participate of all the authors in this research work.

Consent to publish

All the authors are agreed to publish this research work.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

us Salam, W., Tariq, H., Rafeeq, R. et al. New solitary wave solutions to Biswas–Milovic and resonant nonlinear Schrödinger equations. Opt Quant Electron 56, 744 (2024). https://doi.org/10.1007/s11082-024-06286-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11082-024-06286-x

Keywords

Search

Navigation