Skip to main content
SpringerLink
Log in

Optical solitons of time fractional Kundu–Eckhaus equation and massive Thirring system arises in quantum field theory

  • Published:
Optical and Quantum Electronics Aims and scope Submit manuscript

Abstract

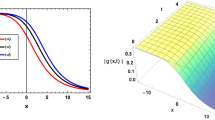
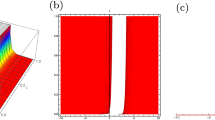
This study focuses on finding the soliton solutions for the time-fractional Kundu–Eckhaus equation and the time-fractional massive Thirring system using the Shehu Adomian decomposition method (SADM). The obtained solitons exhibit periodic shapes in some particular cases. In order to enhance the understanding of the physical characteristics, the presentation of 3D and contour plots involves the selection of specific parameter values for the solutions. To examine the influence of the fractional parameter \(\theta \) on the solutions, two-dimensional graphs are additionally provided. In order to see how the fractional parameter \(\theta \) impacts the solutions, 2D graphs are also presented. In order to validate and show the SADM’s proficiency, we examine the proposed method with regard to fractional order via Atangana–Baleanu in Caputo sense, Caputo, and Caputo–Fabrizio. The uniqueness and convergence of the SADM are presented. The numerical simulations are discussed both numerically and graphically. The results of this research provide perspectives into the intricate dynamics of quantum field theory and help us understand the behaviour of fractional complicated nonlinear equations and their soliton solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Availability of data and materials

Not applicable.

References

  • Adivi Sri Venkata, R.K., Kirubanandam, A., Kondooru, R.: Numerical solutions of time fractional Sawada Kotera Ito equation via natural transform decomposition method with singular and nonsingular kernel derivatives. Math. Methods Appl. Sci. 44(18), 14025–14040 (2021)

    Article  ADS  MathSciNet  Google Scholar 

  • Adomian, G.: A new approach to nonlinear partial differential equations. J. Math. Anal. Appl. 102(2), 420–434 (1984)

    Article  MathSciNet  Google Scholar 

  • Ahmad, S., Salman, Ullah, A., et al.: Bright, dark and hybrid multistrip optical soliton solutions of a non-linear Schrödinger equation using modified extended tanh technique with new Riccati solutions. Opt. Quant Electron. 55, 236 (2023)

  • Akinyemi, L., Iyiola, O.S.: Exact and approximate solutions of time-fractional models arising from physics via Shehu transform. Math. Methods Appl. Sci. 43(12), 7442–7464 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  • Alshabanat, A., Jleli, M., Kumar, S., et al.: Generalization of Caputo-Fabrizio fractional derivative and applications to electrical circuits. Front. Phys. 8, 64 (2020)

    Article  Google Scholar 

  • Atangana, A., Baleanu, D.: New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. Therm. Sci. 20(2), 763–769 (2016)

    Article  Google Scholar 

  • Baber, M.Z., Ahmed, N., Yasin, M.W., et al.: Comparative analysis of numerical with optical soliton solutions of stochastic Gross–Pitaevskii equation in dispersive media. Results Phys. 44, 106175 (2023)

    Article  Google Scholar 

  • Baishya, C., Premakumari, R.N., Samei, M.E., Naik, M.K.: Chaos control of fractional order nonlinear Bloch equation by utilizing sliding mode controller. Chaos Solitons Fractals 174, 113773 (2023)

    Article  MathSciNet  Google Scholar 

  • Bakkyaraj, T., Sahadevan, R.: Approximate analytical solution of two coupled time fractional nonlinear Schrodinger equations. Int. J. Appl. Comput. Math. 2(1), 113–135 (2016)

    Article  MathSciNet  Google Scholar 

  • Baleanu, D., Diethelm, K., Scalas, E., et al.: Series on Complexity, Nonlinearity and Chaos. Fractional Calculus Models and Numerical Methods (2012)

  • Bokhari, A.: Application of Shehu transform to Atangana–Baleanu derivatives. J. Math. Comput. Sci. 20, 101–107 (2019)

    Article  Google Scholar 

  • Caputo, M., Fabrizio, M.: A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 1(2), 1–13 (2015)

    Google Scholar 

  • Eckhaus, W.: The long-time behaviour for perturbed wave-equations and related problems. Trends Appl. Pure Math. Mech. 249, 168–194 (1986)

    Article  ADS  MathSciNet  Google Scholar 

  • Feng, Z., Wang, X.: Explicit exact solitary wave solutions for the Kundu equation and the derivative Schrödinger equation. Phys. Scr. 64(1), 7 (2001)

    Article  CAS  Google Scholar 

  • Goufo, E.F.D., Kumar, S., Mugisha, S.B.: Similarities in a fifth-order evolution equation with and with no singular kernel. Chaos Solitons Fractals 130, 109467 (2020)

    Article  MathSciNet  Google Scholar 

  • Habib, S., Islam, A., Batool, A., et al.: Numerical solutions of the fractal foam drainage equation. GEM-Int. J. Geomath. 12, 1–10 (2021)

    MathSciNet  Google Scholar 

  • Haubold, H.J., Mathai, A.M., Saxena, R.K. : Mittag–Leffler functions and their applications. J. Appl. Math. 2011 (2011)

  • Kanth, A.R., Aruna, K., Raghavendar, K., et al.: Numerical solutions of nonlinear time fractional Klein-Gordon equation via natural transform decomposition method and iterative Shehu transform method. J. Ocean Eng. Sci. (2021). https://doi.org/10.1016/j.joes.2021.12.002

    Article  Google Scholar 

  • Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies. Elsevier, Amsterdam (2006)

    Google Scholar 

  • Korepin, V.E.E.: Direct calculation of the S matrix in the massive Thirring model. Teoreticheskaya i Matematicheskaya Fizika 41(2), 169–189 (1979)

    MathSciNet  Google Scholar 

  • Kumar, S., Ghosh, S., Samet, B., Goufo, E.F.D.: An analysis for heat equations arises in diffusion process using new Yang–Abde–Aty–Cattani fractional operator. Math. Methods Appl. Sci. 43(9), 6062–6080 (2020a)

  • Kumar, S., Nisar, K.S., Kumar, R., Cattani, C., Samet, B.: A new Rabotnov fractional-exponential function-based fractional derivative for diffusion equation under external force. Math. Methods Appl. Sci. 43(7), 4460–4471 (2020b)

  • Kumar, S., Kumar, A., Abbas, S., Al Qurashi, M., Baleanu, D.: A modified analytical approach with existence and uniqueness for fractional Cauchy reaction–diffusion equations. Adv. Differ. Equ. 2020(1), 1–18 (2020c)

  • Kundu, A.: Landau–Lifshitz and higher-order nonlinear systems gauge generated from nonlinear Schrodinger-type equations. J. Math. Phys. 25(12), 3433–3438 (1984)

    Article  ADS  MathSciNet  Google Scholar 

  • Liu, C., Liu, J., Zhou, P., Chen, M.: Exact solutions with bounded periodic amplitude for Kundu equation and derivative nonlinear schrödinger equation. Br. J. Math. Comput. Sci. 16(5), 1–6 (2016)

    Article  ADS  Google Scholar 

  • Luo, X., Nadeem, M.: Mohand homotopy transform scheme for the numerical solution of fractional Kundu–Eckhaus and coupled fractional Massive Thirring equations. Sci. Rep. 13, 3995 (2023)

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  • Maitama, S., Zhao, W.: New integral transform: Shehu transform a generalization of Sumudu and Laplace transform for solving differential equations. Int. J. Anal. Appl. 17(2), 167–190 (2019)

    Google Scholar 

  • Mamta, K., Nehad, A.S., Wajaree, W.: Analytical solution of time-fractional Schrödinger equations via Shehu Adomian Decomposition Method. AIMS Math. 7(10), 19562–19596 (2022)

    Article  MathSciNet  Google Scholar 

  • Mirzazadeh, M., Sharif, A., Hashemi, M.S., et al.: Optical solitons with an extended (3+ 1)-dimensional nonlinear conformable Schrödinger equation including cubic-quintic nonlinearity. Results Phys. 49, 106521 (2023)

    Article  Google Scholar 

  • Mohammadi, F.S., Rahimi, Z., Sumelka, W., et al.: Investigation of free vibration and buckling of Timoshenko nano-beam based on a general form of Eringen theory using conformable fractional derivative and Galerkin method. Eng. Trans. 67(3), 347–367 (2019)

    Google Scholar 

  • Moore, E.J., Sirisubtawee, S., Koonprasert, S.: A Caputo-Fabrizio fractional differential equation model for HIV/AIDS with treatment compartment. Adv. Differ. Equ. 2019(1), 1–20 (2019)

    Article  MathSciNet  Google Scholar 

  • Naik, M.K., Baishya, C., Veeresha, P., Baleanu, D.: Design of a fractional-order atmospheric model via a class of ACT-like chaotic system and its sliding mode chaos control. Chaos Interdiscip. J. Nonlinear Sci. 33(2), 023129 (2023a)

  • Naik, M.K., Baishya, C., Veeresha, P.: A chaos control strategy for the fractional 3D Lotka–Volterra like attractor. Math. Comput. Simul. 211, 1–22 (2023b)

  • Nasreen, N., Lu, D., Zhang, Z., et al.: Propagation of optical pulses in fiber optics modelled by coupled space-time fractional dynamical system. Alex. Eng. J. 73, 173–187 (2023)

    Article  Google Scholar 

  • Premakumari, R.N., Baishya, C., Kaabar, M.K.: Dynamics of a fractional plankton-fish model under the influence of toxicity, refuge, and combine-harvesting efforts. J. Inequalities Appl. 2022(1), 137 (2022)

    Article  MathSciNet  Google Scholar 

  • Rashid, S., Khalid, A., Sultana, S., et al.: A novel analytical view of time-fractional Korteweg–De Vries equations via a new integral transform. Symmetry 13(7), 1254 (2021)

    Article  ADS  Google Scholar 

  • Ravi Kanth, A.S.V., Aruna, K., Raghavendar, K.: Natural transform decomposition method for the numerical treatment of the time fractional Burgers–Huxley equation. Numer. Methods Partial Differ. Equ. 39(3), 2690–2718 (2023)

    Article  MathSciNet  Google Scholar 

  • Ray, S.S., Bera, R.K.: An approximate solution of a nonlinear fractional differential equation by Adomian decomposition method. Appl. Math. Comput. 167(1), 561–571 (2005)

    MathSciNet  Google Scholar 

  • Ray, S.S., Chaudhuri, K.S., Bera, R.K.: Analytical approximate solution of nonlinear dynamic system containing fractional derivative by modified decomposition method. Appl. Math. Comput. 182(1), 544–552 (2006)

    MathSciNet  Google Scholar 

  • Rizwan, M., Farman, M., Akgül, A., et al.: Variation in electronic and optical responses due to phase transformation of SrZrO 3 from cubic to orthorhombic under high pressure: a computational insight. Indian J. Phys. 96, 1–9 (2021)

    Article  ADS  Google Scholar 

  • Rupa, M.L., Aruna, K.: Optical soliton solutions of nonlinear time fractional Biswas–Milovic equation. Optik 270, 169921 (2022)

    Article  ADS  Google Scholar 

  • Sabir, Z., Raja, M.A.Z., Baleanu, D.: Fractional mayer neuro-swarm heuristic solver for multi-fractional order doubly singular model based on lane–emden equation. Fractals 29(05), 2140017 (2021)

    Article  ADS  Google Scholar 

  • Sabi’u, J., Shaayesteh, M.T., Taheri, A., et al.: New exact solitary wave solutions of the generalized (3+ 1)-dimensional nonlinear wave equation in liquid with gas bubbles via extended auxiliary equation method. Opt. Quant Electron. 55, 586 (2023)

    Article  Google Scholar 

  • Shah, F.A., Abass, R., Debnath, L.: Numerical solution of fractional differential equations using Haar wavelet operational matrix method. Int. J. Appl. Comput. Math. 3(3), 2423–2445 (2017)

    Article  MathSciNet  Google Scholar 

  • Tuan, N.H., Mohammadi, H., Rezapour, S.: A mathematical model for COVID-19 transmission by using the Caputo fractional derivative. Chaos Solitons Fractals 140, 110107 (2020)

    Article  MathSciNet  PubMed  PubMed Central  Google Scholar 

  • Veeresha, P., Prakasha, D.G., Kumar, S.: A fractional model for propagation of classical optical solitons by using nonsingular derivative. Math. Methods Appl. Sci. (2020)

  • Yi, Y., Liu, Z.: The bifurcations of traveling wave solutions of the Kundu equation. J. Appl. Math. 2013 (2013)

  • Zhang, H.: Various exact travelling wave solutions for Kundu equation with fifth-order nonlinear term. Rep. Math. Phys. 65(2), 231–239 (2010)

    Article  ADS  MathSciNet  Google Scholar 

  • Zhang, W., Qin, Y., Zhao, Y., Guo, B.: Orbital stability of solitary waves for Kundu equation. J. Differ. Equ. 247(5), 1591–1615 (2009)

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors express their gratitude to the anonymous reviewers for their insightful comments and suggestions to enhance the quality of the manuscript.

Funding

Not applicable.

Author information

Authors and Affiliations

  1. Department of Mathematics, School of Advanced Sciences, Vellore Institute of Technology, Vellore, 632014, India

    M. L. Rupa & K. Aruna

Authors
  1. M. L. Rupa
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. Aruna
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

MLR: visualization, methodology, validation, writing original draft. KA: methodology, investigation, supervision, writing original draft, validation, visualization.

Corresponding author

Correspondence to K. Aruna.

Ethics declarations

Ethical approval

Not applicable.

Conflict of interest

There is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rupa, M.L., Aruna, K. Optical solitons of time fractional Kundu–Eckhaus equation and massive Thirring system arises in quantum field theory. Opt Quant Electron 56, 460 (2024). https://doi.org/10.1007/s11082-023-05914-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11082-023-05914-2

Keywords

Search

Navigation