Abstract
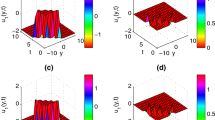
Fractional Phi-4 equation plays a crucial role in many studies of nuclear and particle physics. In this paper, the fractional Phi-4 equation is studied for two recently developed definitions of fractional derivatives and the comparison of the results with both derivatives is presented. The wave solutions of fractional Phi-4 equation are obtained using the extended \(\sinh\)-Gordon equation expansion method. The beta and M-truncated fractional effects are considered. New complex trigonometric and complex hyperbolic function solutions are retrieved. Dark solitons and periodic solitary waves are observed for obtained solutions. The wave profiles obtained for the beta and M-truncated derivatives are compared for different values of fractional order using graphical simulations. The presented results are novel and the extended sinh-Gordon equation expansion method has been utilized to investigate fractional Phi-4 equation with beta and M-truncated derivative for the first time in this work.




Similar content being viewed by others
Data availability
Not applicable.
References
Abdelrahman, M.A.E., Hassan, S.Z., Alomair, R.A., Alsaleh, D.M.: Fundamental solutions for the conformable time fractional Phi-\(4\) and space-time fractional simplified MCH equations. AIMS Math. 6, 6555–6568 (2021)
Akram, G., Sadaf, M., Abbas, M., Zainab, I., Rijaa, S.: Efficient techniques for traveling wave solutions of time-fractional Zakharov-Kuznetsov equation. Math. Comput. Simul. 193, 607–622 (2022)
Akram, G., Sadaf, M., Zainab, I.: Observations of fractional effects of \(\beta\)-derivative and M-truncated derivative for space time fractional Phi-4 equation via two analytical techniques. Chaos Solitons Fract. 154, 111645 (2022)
Dubey, V.K., Singh, J., Alshehri, A.M., Dubey, S., Kumar, D.: Analysis of local fractional coupled Helmholtz and coupled Burgers equations in fractal media. AIMS Math. 7(5), 8080–8111 (2022)
Faridi, W.A., Asjad, M.I., Jhangeer, A.: The fractional analysis of fusion and fission process in plasma physics. Phys. Scr. 96(10), 104008 (2021)
Irshad, A., Ahmed, N., Khan, U., Din, S.T.M., Khan, I., Sherif, E.S.M.: Optical solutions of Schrödinger equation using extended sinh-Gordon equation expansion method. Front. Phys. 8, 73 (2020)
Kamran, M., Majeed, A., Li, J.: On numerical simulations of time fractional Phi-four equation using Caputo derivative. Comput. Appl. Math. 40(7), 257 (2021)
Khater, M.M.A., Mousa, A.A., El-Shorbagy, M.A., Attia, R.A.M.: Analytical and semi-analytical solutions for Phi-\(4\) equation through three recent schemes. Res. Phys. 22, 103954 (2021)
Kumar, D., Manafian, J., Hawlader, F., Ranjbaran, A.: New closed form soliton and other solutions of the Kundu-Eckhaus equation via the extended sinh-Gordon equation expansion method. Opt. Int. J. Light Electron Opt. 160, 159–167 (2018)
Kumar, V.S., Rezazadeh, H., Eslami, M., Izadi, F., Osman, M.S.: Jacobi Elliptic function expansion method for solving KdV equation with conformable derivative and dual-power law nonlinearity. Opt. Int. J. Light Electron Opt. 5(5), 127 (2019)
Li, Z., Han, T., Huang, C.: Bifurcation and new exact traveling wave solutions for time-space fractional Phi-4 equation. AIP Adv. 10(11), 115113 (2020)
Liu, J.G., Yang, X.J., Wang, J.J.: A new perspective to discuss Korteweg-de Vries-like equation. Phys. Lett. A 451, 128429 (2022)
Liu, J.G., Yang, X.J., Geng, L.L., Yu, X.J.: On fractional symmetry group scheme to the higher-dimensional space and time fractional dissipative Burgers equation. Int. J. Geom. Methods Mod Phys 19(11), 2250173 (2022)
Lu, D., Tariq, K.U., Osman, M.S., Baleanu, D., Younis, M., Khater, M.M.A.: New analytical wave structures for the (3+1)-dimensional Kadomtsev-Petviashvili and the generalized Boussinesq models and their applications. Res. Phys 14, 102491 (2019)
Lu, D., Osman, M.S., Khater, M.M.A., Attia, R.A.M., Baleanu, D.: Analytical and numerical simulations for the kinetics of phase separation in iron (Fe-Cr-X(X=Mo, Cu)) based on ternary alloys. Phys. A 537, 122634 (2020)
Osman, M.S.: One-soliton shaping and inelastic collision between double solitons in the fifth-order variable-coefficient Sawada-Kotera equation. Nonlinear Dyn. 96(2), 1491–1496 (2019)
Osman, M.S., Lu, D., Khater, M.M.A., Attia, R.A.M.: Complex wave structures for abundant solutions related to the complex Ginzburg-Landau model. Opt. Int. J. Light Electron Opt. 192, 162927 (2019)
Rahman, F., Ali, A., Saifullah, S.: Analysis of time-fractional \(\phi ^{4}\)-equation with singular and non-singular kernels. Int. J. Appl. Comput. Math. 7, 192 (2021)
Rezazadeh, H., Tariq, H., Eslami, M., Mirzazadeh, M., Zhou, Q.: New exact solutions of nonlinear conformable time-fractional Phi-\(4\) equation. Chin. J. Phys. 56(6), 2805–2816 (2018)
Riaz, M.B., Awrejcewicz, J., Jhangeer, A.: Optical solitons with Beta and M-truncated derivatives in nonlinear negative-index materials with Bohm potential. Materials 14(18), 5335 (2021)
Singh, J., Ganbari, B., Kumar, D., Baleanu, D.: Analysis of fractional model of guava for biological pest control with memory effect. J. Adv. Res. 32, 99–108 (2021)
Singh, J., Alshehri, A.M., Momani, S., Hadid, S., Kumar, D.: Computational analysis of fractional diffusion equations occurring in oil pollution. Mathematics 10(20), 3827 (2022)
Sirisubtawee, S., Koonprasert, S., Sungnul, S., Leekparn, T.: Exact traveling wave solutions of the space-time fractional complex Ginzburg-Landau equation and the space-time fractional Phi-\(4\) equation using reliable methods. Adv. Differ. Equ. 2019(1), 219 (2019)
Yusuf, A., Inc, M., Baleanu, D.: Optical solitons with M-truncated and beta derivatives in nonlinear optics. Front. Phys. 7, 126 (2019)
Zou, G.A., Wang, B.: Solitary wave solutions for nonlinear fractional Schrödinger equation in Gaussian nonlocal media. Appl. Math. Lett. 88, 50–57 (2019)
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
GA participated in the conceptualization, data curation, investigation, methodology, software implementation, validation, visualization and writing the original draft. SA participated in the conceptualization, administration, validation, visualization and writing of the manuscript. MS participated in the formal analysis, investigation, supervision, review and editing of the manuscript. MM participated in the data curation, formal analysis, software and writing of the original draft. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interests.
Ethical approval
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Akram, G., Arshed, S., Sadaf, M. et al. Comparison of fractional effects for Phi-4 equation using beta and M-truncated derivatives. Opt Quant Electron 55, 282 (2023). https://doi.org/10.1007/s11082-023-04549-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-023-04549-7