1 Introduction

Fiber optics communication is considered to be one of the most innovative methods of communication which has originated about 40 years ago. Radio-over-fiber (RoF) was introduced for the very first time in 1990 and since then it has been widely used whilst showing a great approach to communication system due to its high bandwidth, low losses, low power consummation, cost-effective, and other of fiber-optic signal propagation properties, including recent developments of Microwave Photonics Analog Link (MPAL) tunable amplifiers, and photonic mixer up converters and down converters (Cooper 1990; Haas and Murphy 2007; Masella et al. 2009; Ali et al. 2021; Mirza et al. 2021a; Henan Zeng et al. 2022). RoF as an analogue communications system includes RF and optical fiber components such as: Photodiode, filters, optical amplifiers, optical fiber, optical modulator, and laser. So far optical communication system has resulted to be the best solution to modern mode communication due to above stated properties; however, optical communication has its own limitations as well, including non-linearity as a feature that produces Intermodulation Distortions (IMDs), loses and dispersion of signal. One of the most challenging tasks is the suppressing of nonlinear distortions, which strongly affects the performance of the MPAL.

Dual-parallel Mach–Zehnder modulator (DMZM) is most commonly used modulator for elimination or suppression of IMDs and possibly for dynamic increase range which requires complex radio-frequency arrangement and linearization (Ali et al. 2021; Xu et al. 2016). Whereas Third Intermodulation Distortion (IMD3) is the most rigorous in signal linearization, down to being very close to transmitted signal and limiting free dynamic range. Conversely, when signals are very close to each other, the Second Intermodulation Distortions (IMD2) along Second Order Harmonics (SOH) will experience severe distortions, subsequently many linearization techniques have been developed to supressing IMDs and improving Spurious-Free Dynamic Range (SFDR) (Xu et al. 2016; Pail et al. 2018; Yao 2009; Mérolla et al. 1999; Huang et al. 2012; Shaqiri et al. 2020; Shaqiri and Haxha 2020).

In (Jiang et al. 2016) improved linearized Microwave Photonics Analog Link (MPAL) with double dual-parallel Mach–Zehnder modulator and a differential balanced photodetector is reported. In this paper, polarization maintained (PM) based optical components are used for better system stability. The developed theoretical model of the proposed system illustrates the elimination of even-order distortions and a high suppression to the IMD3 at the BPD. Consequently, the fundamental Signal to Interference ratio (S/I) of 60 dB was experimentally achieved. Experimental results, simultaneously, demonstrate a significant increase of Second-order Spurious free Dynamic Range (SFDR2) and Third-order Spurious-free Dynamic Range (SFDR3) by 19.5 dB and 3.1 dB, respectively. The performance analysis of microwave photonic frequency conversion has been recorded to use a double-sideband suppressed-carrier and balance based on DPMZM (Shaqiri et al. 2020). The double-sideband technique has been used to suppress high harmonics and high Intermodulation’s, as well as achieve frequency conversion signals. However, as suggested from the title, in Mirza et al. 2021b, only manage to suppress theoretically IMDs and high harmonics.

Based on Dual-parallel Mach–Zehnder modulator (DPMZM), a linearization MPAL with IMD3 elimination is proposed and experimentally demonstrated (W. Jiang Et Al 2015). Using symmetrical side band modulation, in this paper, the authors have managed to eliminate IMD3, in theory, by using two shifters and 3 dB power combiners. It has also been demonstrated experimentally the 45 dB suppression of the IMD3. Nevertheless, this paper only reports the elimination of IMD3 with all the other Harmonics and IMD’s that has been left; consequently, in our paper we have used similar technique, whereas, we have managed to remove all IMD’s. A dual-wavelength linearization of analogue photonic link, based on PM-IM conversion, has been proposed and demonstrated in Qin and Jiang (2015). Furthermore, a phase modulator which exhibits different electro-optic modulation index was used. Primarily, this paper reports and experimentally demonstrate a suppression of IMD3 by 14.54 dB based on two different channels with opposite field which than fabricate a possible suppression of IMD3.

Multi-octave linearized analogue photonic link based on a polarization DPMZM is proposed in Zhang et al. (2018). An elimination of IMD2 and suppression of IMD3 is reported in this research which is profoundly based on the integrated polarization multiplexing DPMZM with free dynamic range of 82 dB. However, in this paper IMD2 has been completely eliminated whereas IMD3 has only been suppressed, while in our proposed structure all IMD’s are completely eliminated.

In (Zou et al. 2016) is proposed and demonstrated a high linear analogue photonic link, based on a D-DPMZM with BPD. Moreover, third IMD3 and Second-Order Distortions (SOD) products have been completely eliminated. We developed systems modelling and simulations of a novel two-tone microwave frequency two D-DPMZM consist of two sub-dual electrode MZMs and two balance photo-detector combined by using a 3 dB power combiner. The proposed MPAL systems requires less RF shifters and it would be much easier to be implement in practice as also shown in Xie et al. (2016) whereas parts of the system has already been experimentally demonstrated. Furthermore, to the best of our knowledge, this is the first study that shows a complete mathematical modelling design, analyses, and optimises the proposed unique MPAL, and shows that the proposed system model and simulations match exceptionally well.

2 Mathematical model of the proposed system

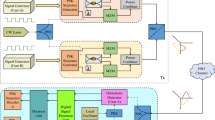
The schematic diagram of proposed photonic link where all IMDs along Harmonics Distortions which are based on two D-DPMZM – have been eliminated by using balanced-photo-detectors, shown in the Fig. 1. In this configuration, we have used two-tone microwave frequency of 17 GHz and 17.5 GHz using RF shifters by 90 degrees and 270 degrees, respectively. The two D-DPMZM consist of two sub-dual electrode MZMs and two balance photo-detector combined by using a 3 dB power combiner.

Fig. 1
figure 1

Schematic diagram of the proposed AMPL system configuration using two D-DPMZM with two input frequencies

Full size image

Two RF signals are combined by RF combiner and then are shifted by 90 degrees for upper and lower arm of MZM1 (D-DPMZM1) while frequency one is shifted by 270 degrees whereas frequency two is shifted by 90 degrees for upper and lower arm of \({\mathrm{MZM}}_{2}\) (D-DPMZM1). In D-DPMZM2 the RF frequencies are combined and then shifted by 270 degrees for upper and lower arm of MZM1 (D-DPMZM2), frequency one is shifted by 90 degrees and frequency two is shifted by 270 degrees for upper and lower arm of \({\mathrm{MZM}}_{2}\) (D-DPMZM2). External DC bias is set to maximum for MZM1 and to quadrature for MZM2 for both D-DPMZMs. In addition, frequencies than are combined by 3 dB power combiner and detected by balanced photo-detector. Results show that proposed configuration allows elimination of all IMDs and all even harmonic distortions.

The drive voltage with DC biases of the D-DPMZM1 for the schematic configuration illustrated in Fig. 1 can be expressed as:

$$ Q_{11} (t) = V_{m} \left\{ {\cos (\omega_{1} t + \frac{\pi }{2}) + \cos (\omega_{2} t + \frac{\pi }{2})} \right\} + V_{\pi } $$
(1)
$$ Q_{12} (t) = V_{m} \left\{ {\cos (\omega_{1} t + \frac{\pi }{2}) + \cos (\omega_{2} t + \frac{\pi }{2})} \right\} $$
(2)
$$ \begin{gathered} Q_{21} (t) = V_{m} \left\{ {\cos (\omega_{1} t - \frac{\pi }{2}) + \cos (\omega_{2} t + \frac{\pi }{2})} \right\} + \frac{{V_{\pi } }}{2} \hfill \\ \hfill \\ \end{gathered} $$
(3)
$$ Q_{22} (t) = V_{m} \left\{ {\cos (\omega_{1} t - \frac{\pi }{2}) + \cos (\omega_{2} t + \frac{\pi }{2})} \right\} $$
(4)

where \({Q}_{11}\left(\mathrm{t}\right)\mathrm{ and }{Q}_{12}\left(\mathrm{t}\right)\) are drive voltages on two electrodes of MZM1 (D-DPMZM1); \({Q}_{21}\left(\mathrm{t}\right)\mathrm{ and }{Q}_{12}\left(\mathrm{t}\right)\) are drive voltages on two electrodes of MZM2 (D-DPMZM1); \({\mathrm{V}}_{\mathrm{m}}\) represent the amplitude of the RF input signals. The laser power is expressed as: \({E}_{\mathrm{in}}\left(t\right)={E}_{c}{\mathrm{e}}^{\mathrm{j}{\omega }_{\mathrm{c}}t}\) where the Ec is the input power and ωc is the angular frequency of the laser, consequently the output optical power in MZM1 (D-DPMZM1) can be expressed as:

$$ E_{{out1D - DPMZ_{1} }} (t) = E_{in} (t)\left\{ {\exp (j\pi \frac{{Q_{11} (t)}}{{V_{\pi } }}) + \exp ( - j\pi \frac{{Q_{12} (t)}}{{V_{\pi } }})} \right\} $$
(5)

The output optical power in MZM2 (D-DPMZM1) can be expressed as:

$$ E_{{out2D - DPMZ_{1} }} (t) = E_{in} (t)\left\{ {\exp (j\pi \frac{{Q_{21} (t)}}{{V_{\pi } }}) + \exp ( - j\pi \frac{{Q_{22} (t)}}{{V_{\pi } }})} \right\} $$
(6)

If \(m=\frac{\pi {V}_{m}}{{V}_{\pi }}\) than by substituting Eq. (1) and (2) into Eq. (5) we obtain:

$$ E_{{out1D - DPMZ_{1} }} (t) = E_{in} (t)\left\{ \begin{gathered} \exp (jm\left\{ {\sin (\omega_{1} t) + \sin (\omega_{2} t)} \right\} + j\pi ) \hfill \\ + \exp ( - jm\left\{ {\sin (\omega_{1} t) + \sin (\omega_{2} t)} \right\}) \hfill \\ \end{gathered} \right\} $$
(7)

Applying a Jacobi-Anger Expansion in Eq. (7), we obtain:

$$ E_{{out2D - DPMZM_{1} }} (t) = E_{in} (t)\sum\limits_{n,m = - \infty }^{\infty } {J_{n} (m)} J_{m} (m)e^{{j(n\omega_{1} t + \omega_{2} t)}} \left[ {( - 1)^{n + m} e^{j\pi } + 1} \right] $$
(8)

Similarly, by substituting Eq. (3) and (4) into Eq. (6), we can derive the output optical power in MZM2 (D-DPMZM1):

$$ E_{{out2D - DPMZM_{1} (t)}} = E_{in} (t)\left\{ \begin{gathered} \exp (jm\left\{ {\sin (\omega_{1} t) - \sin (\omega_{2} t)} \right\}) + j\frac{\pi }{2} \hfill \\ + \exp ( - jm\left\{ {\sin (\omega_{1} t) - \sin (\omega_{2} t)} \right\}) \hfill \\ \end{gathered} \right\} $$
(9)

Applying a Jacobi-Anger Expansion in Eq. (9), we find:

$$ E_{{out2D - DPMZM_{1} }} (t) = E_{in} (t)\sum\limits_{n,m = - \infty }^{\infty } {j_{n} (m)} j_{m} (m)e^{{j(n\omega_{1} t + \omega_{2} t)}} \left[ \begin{gathered} \left\{ {( - 1)^{m} + 1} \right\}e^{{j\frac{\pi }{2}}} \hfill \\ + ( - 1)^{n} + 1 \hfill \\ \end{gathered} \right] $$
(10)

Combined power of the two MZMs will represent the optical power for D-DPMZM1. The signal after 3 dB power combiner can be expressed as:

$$ E_{{1D - DPMZM_{1} }} (t) = \frac{{E_{{out1D - DPMZM_{1} }} (t) + E_{{out2D - DPMZM_{1} }} (t)}}{\sqrt 2 } $$
(11)
$$ E_{{1D - DPMZM_{1} }} (t) = \frac{{E_{{out1D - DPMZM_{1} }} (t) - E_{{out2D - DPMZM_{1} }} (t)}}{\sqrt 2 } $$
(12)

The generated photocurrent I(t) after the balance-photodetector is:

$$ I_{{PDD - DPMZM_{1} }} (t) = R\left[ \begin{gathered} E_{{out1D - DPMZM_{1} }} (t).E_{{out1D - DPMZM_{1} }} (t)^{*} - \hfill \\ E_{{out2D - DPMZM_{1} }} (t).E_{{out2D - DPMZM_{1} }} (t)^{*} \hfill \\ \end{gathered} \right] $$
(13)

where \(\mathcal{R}\) is responsivity of the photodetector. By deploying Tayler series expansion to the third order in m, following expression can be derived.

$$ I_{{PDD - DPMZM_{1} }} (t) = - \frac{1}{2}RP_{in} \left\{ \begin{gathered} 8m(\cos (\omega_{1} t) + \sin (\omega_{2} t)) + \hfill \\ 4m^{2} (\cos (2\omega_{1} t) - \cos (2\omega_{2} t)) \hfill \\ + 4m^{3} \left( \begin{gathered} \sin (3\omega_{1} t) + \sin (3\omega_{2} t) \hfill \\ - \sin (\omega_{1} t) - \sin (\omega_{2} t) \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right\} + o(m)^{4} $$
(14)

Similarly, we can derive equations for D-DPMZM2 as follows:

$$ Q_{11} (t) = V_{m} \left\{ {\cos (\omega_{1} t - \frac{\pi }{2}) + \cos (\omega_{2} t - \frac{\pi }{2})} \right\} + V_{\pi } $$
(15)
$$ Q_{12} (t) = V_{m} \left\{ {\cos (\omega_{1} t + \frac{\pi }{2}) + \cos (\omega_{2} t + \frac{\pi }{2})} \right\} $$
(16)
$$ Q_{21} (t) = V_{m} \left\{ {\cos (\omega_{1} t + \frac{\pi }{2}) + \cos (\omega_{2} t - \frac{\pi }{2})} \right\} + \frac{{V_{\pi } }}{2} $$
(17)
$$ Q_{22} (t) = V_{m} \left\{ {\cos (\omega_{1} t + \frac{\pi }{2}) + \cos (\omega_{2} t - \frac{\pi }{2})} \right\} $$
(18)

where \({Q}_{11}\left(t\right)\mathrm{ and }{Q}_{12}\left(t\right)\) are drive voltages on two electrodes of MZM1 (D-DPMZM2); \({Q}_{21}\left(\mathrm{t}\right)\mathrm{ and }{Q}_{12}\left(\mathrm{t}\right)\) are drive voltages on two electrodes of MZM2 (D-DPMZM2); \({\mathrm{V}}_{\mathrm{m}}\) represent the amplitude of the RF input signals. The laser power is expressed as: \({E}_{\mathrm{in}}\left(t\right)={E}_{\mathrm{c}}{\mathrm{e}}^{\mathrm{j}{\omega }_{\mathrm{c}}\mathrm{t}}\) where the Ec is the input power and ωc is the angular frequency of the laser, consequently the output optical in MZM1 (D-DPMZM2) can be expressed as:

$$ E_{out1D - DPMZ2} (t) = E_{in} (t)\left\{ {\exp (j\pi \frac{{Q_{11} (t)}}{{V_{\pi } }}) + \exp ( - j\pi \frac{{Q_{12} (t)}}{{V_{\pi } }})} \right\} $$
(19)

And the output optical power in MZM2 (D-DPMZM2) can be expressed as:

$$ E_{{out2D - DPMZ_{2} }} (t) = E_{in} (t)\left\{ {\exp (j\pi \frac{{Q_{21} (t)}}{{V_{\pi } }}) + \exp ( - j\pi \frac{{Q_{22} (t)}}{{V_{\pi } }})} \right\} $$
(20)

If \(m=\frac{\pi {V}_{m}}{{V}_{\pi }}\) than by substituting Eq. (15) and (16) into Eq. (19), we obtain:

$$ E_{out1D - DPMZ2} (t) = E_{in} (t)\left\{ \begin{gathered} \exp (jm\left\{ {\sin (\omega_{1} t) + \sin (\omega_{2} t)} \right\} + j\pi ) \hfill \\ + \exp (jm\left\{ {\sin (\omega_{1} t) + \sin (\omega_{2} t)} \right\}) \hfill \\ \end{gathered} \right\} $$
(21)

Applying a Jacobi-Anger Expansion in Eq. 20 we get:

$$ E_{out1D - DPMZM2} (t) = E_{in} (t)\sum\limits_{n,m = - \infty }^{\infty } {J_{n} (m)} J_{m} (m)e^{{j(n\omega_{1} t + \omega_{2} t)}} \left[ {( - 1)^{n + m} e^{j\pi } + 1} \right] $$
(22)

Similarly, by substituting Eq. (17) and (18) into Eq. (20), we can derive the output optical power in MZM2 (D-DPMZM2):

$$ E_{{out2D - DPMZM_{2} (t)}} = E_{in} (t)\left\{ \begin{gathered} \exp (jm\left\{ { - \sin (\omega_{1} t) + \sin (\omega_{2} t)} \right\}) + j\frac{\pi }{2} \hfill \\ + \exp ( - jm\left\{ { - \sin (\omega_{1} t) + \sin (\omega_{2} t)} \right\}) \hfill \\ \end{gathered} \right\} $$
(23)

Applying a Jacobi-Anger Expansion in Eq. (22), we obtain:

$$ E_{out2D - DPMZM2} (t) = E_{in} (t)\sum\limits_{n,m = - \infty }^{\infty } {j_{n} (m)} j_{m} (m)e^{{j(n\omega_{1} t + \omega_{2} t)}} \left[ \begin{gathered} \left\{ {( - 1)^{m} + 1} \right\}e^{{j\frac{\pi }{2}}} \hfill \\ + ( - 1)^{n} + 1 \hfill \\ \end{gathered} \right] $$
(24)

Combined power of the two MZMs will represent the optical power for D-DPMZM1. The signal after 3 dB power combiner can be expressed as:

$$ E_{{2D - DPMZM_{2} }} (t) = \frac{{E_{{out1D - DPMZM_{2} }} (t) + E_{out2D - DPMZM2} (t)}}{\sqrt 2 } $$
(25)
$$ E_{2D - DPMZM2} (t) = \frac{{E_{out1D - DPMZM2} (t) - E_{{out2D - DPMZM_{2} }} (t)}}{\sqrt 2 } $$
(26)

The generated photocurrent \({\mathrm{I}}_{\mathrm{PD}\_{\mathrm{D}-\mathrm{DPMZM}}_{2}}\left(\mathrm{t}\right)\) after the balance-photodetector is:

$$ I_{PDD - DPMZM2} (t) = R\left[ \begin{gathered} E_{{out1D - DPMZM_{2} }} (t).E_{{out1D - DPMZM_{2} }} (t)^{*} - \hfill \\ E_{out2D - DPMZM2} (t).E_{out2D - DPMZM2} (t)^{*} \hfill \\ \end{gathered} \right] $$
(27)

where \(\mathcal{R}\) is responsivity of photodetector. By using Tayler series expansion to the third order in m, following expression can be derived:

$$ I_{PDD - DPMZM2} (t) = - \frac{1}{2}RP_{in} \left\{ \begin{gathered} 8m(\cos (\omega_{1} t) + \sin (\omega_{2} t)) + \hfill \\ - 4m^{2} (\cos (2\omega_{1} t) - \cos (2\omega_{2} t)) \hfill \\ + 4m^{3} \left( \begin{gathered} \sin (3\omega_{1} t) + \sin (3\omega_{2} t) \hfill \\ - \sin (\omega_{1} t) - \sin (\omega_{2} t) \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right\} + o(m)^{4} $$
(28)

Combining power after two balance-photodetectors

$$ I_{PD} (t) = I_{PDD - DPMZM1} (t) + I_{PDD - DPMZM2} (t) $$
(29)

Then we obtain:

$$ I_{PD} (t) = RP_{in} \left\{ \begin{gathered} 16m(\cos (\omega_{1} t) + \sin (\omega_{2} t)) + \hfill \\ + 8m^{3} \left( \begin{gathered} \sin (3\omega_{1} t) + \sin (3\omega_{2} t) \hfill \\ - \sin (\omega_{1} t) - \sin (\omega_{2} t) \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right\} + o(m)^{4} $$
(30)

From results in Eq. (28), it can be seen that the third order Intermodulation Distortion of frequency \({2\omega }_{2}{-\omega }_{1}\) and \(2{\omega }_{1}-{\omega }_{2}\) is eliminated. Second order harmonic and intermodulation of frequency is \({\upomega }_{2}{-\upomega }_{1}\),\({\upomega }_{1}-{\upomega }_{2}\), and \({2\upomega }_{2}{-2\upomega }_{1}\),\(2{\upomega }_{1}-2{\upomega }_{2}\). We have used the Tayler series to higher order (up to ninth order) and to all intermodulation distortions and even harmonic distortions does not exist which means that the modulation index increases the IMDs and even harmonic distortions will not exist in this model.

3 Simulation results and discussions

Simulation results are undertaken based on the developed mathematical model representing the novel RF system configuration Fig. 1. As stated above, the schematic configuration of proposed microwave photonic signal linearization includes laser, two tone microwave frequencies, six shifters four of which are 90-degrees and two 270-degree, 3 dB power combiner, two D-DPMZM and two balance-photodetector. Laser optical power of 20dBm is used, and two signals with frequency of 17 GHz and 17.5 GHz are investigated. The input laser light is split in four equal paths and modulated at four sub-MZMs.

In D-DPMZM1 lower and upper branch of MZM1 the RF signal ω1 and ω2 are shifted by 90 degrees, while in \({\mathrm{MZM}}_{2}\) RF signal ω1 is shifted by \(\frac{\pi }{2}\) and ω2 is shifted by −\(\frac{\pi }{2}\), frequencies are than combined by RF combiner and modulated in upper and lower branch. Output modulated signal from \({\mathrm{MZM}}_{1}\) and \({\mathrm{MZM}}_{2}\) are combined by 3 dB power combiner than detected by balanced-photodetector. In D-DPMZM2 RF signal are shifted and combined same as in D-DPMZ1 but with opposite phase, output modulated signal from MZM1 and MZM2 are combined and detected by balanced-photodetector two. Electrical signal from both balanced-photodetector is combined, obtained results are shown in Fig. 2.

Fig. 2
figure 2

Electrical spectrum of the proposed structure; A Two single subcarriers from D-DPMZM1 without any intermodulation distortions, B Two single subcarriers from D-DPMZM2 without any intermodulation distortions, C Two single subcarriers after combining without any SOH, D shows the non-existence of IMD2 and SOH

Full size image

Figure 2A shows signal output from D-DPMZM1, which shows elimination of IMDs, however SOH is present as shown Eq. (14). Similarly, Fig. 2B illustrates the output from D-DMZM2 with opposite SOH field shown in Eq. (27) which enables the elimination of SOH. Therefore, SFDR in this system is limited only by Third Order Harmonics (TOH). The TOH are quite far from fundamental signal and can be easily filter by using low power electrical filter.

By comparing our obtained results with our previous experimental results of similar RF system publish recently in Zou et al. (2016), it can be confirmed that we have managed to improve a signal linearization significantly. In the published paper (Zou et al. 2016), we have demonstrated suppression of IMDs and SOH experimentally and benchmarked by the developed mathematic model, however in Zou et al. (2016) only IMD’s and SOH are suppressed, shown in Eq. (14) Sect. 2 Mathematic Modelling, where in this proposed RF system configuration, we have eliminated SOH Fig. 2D and all other IMD’s Fig. 2C. Obtained simulations shown in Fig. 2C have been backed up by the developed mathematical modelling Eq. (28), showing Tayler series up to forth order which confirms that the IMD’s and SOH do not exist. In order to verify simulation results, we have used Tayler series up to 9th order and still evidence the clear the match.

In the Fig. 3A, we present the SFDR performance analysis of the proposed system. As we have mathematically presented, the proposed system in an ideal condition, it will not produce any IMD3, IMD2 or SOH, however in real life it is almost impossible to have an ideal condition, therefore we have changed the modulator parameter to match with our practical laboratory components (shown in Table 1); modulators and RF shifters for 1 degree to measure the SFDR3. Figure 3A shows SFDR3 for the proposed link is 120.5 dB.Hz1/2 from −170 noise floor.

Fig. 3
figure 3

A SFDR performance of proposed AMPL with Dual Parallel MZMs, B System stability analyses C Two single subcarriers after changing RF shifters for 1 degree, D. Two single subcarriers after changing RF shifters for 1 degree and adding fiber between BPDs and 3 dB power combiner

Full size image
Table1 MZMS Parameters used in our simulation
Full size table

To demonstrate the performance of the proposed RF system configuration with reference to the bias drift, we have investigated the following CNR for IMD3, IMD2 and SOH, shown in Fig. 3B. As it can be seen from results, the CIR for IMD3, IMD2 and SOH are almost constant at a bias drift of up to ± 0.5 V, therefore system is stable. Due to fact that IMDs and SOH are eliminated, the propose system performance is stable as the operating points voltage changes.

Next, we have tested the system purity by varying the parameters of the modulator (shown in Table. 1) to match with practical modulators and by changing RF shifters for one degree. As can be seen, the obtained results are similar to those in Fig. 3C. Furthermore, by using the same parameters for modulators and RF shifters, we have tasted the system further by adding different fiber lengths between 3 dB combiner and BPDs (20-m fiber between 3 dB combiner and BPD1 and 19-m fiber between 3 dB combiner and BPD2) results are shown in Fig. 3D. Simulation from Fig. 3D shows confirms that there is no SOH, however, if the length of fiber optic cable is not the same, then IMD3 starts coming up the noise floor.

The proposed model consists of 6 RF shifters, 4 splitters and 4 combiners, therefore, it known there will be losses. In this regard, in the simulation model we have included all potential losses which might occur in practice. Attenuates on each connection have been considered in order to present the losses for each shifter, splitter and combiner, obtained result are shown in Fig. 4A. Losses added to the system is 42 dB, hence the dynamic range is not as shown in an ideal case in Fig. 2, however, the obtained results demonstrate that the dynamic range has not been decreased in regard to TOH and TOH which have been suppressed under the noise floor. Furthermore, the system performance has been tested by changing the input of the laser to 15 dB, which includes losses as mention above in order to investigate the effects on SFDR, obtained result are shown in Fig. 4B.

Fig. 4
figure 4

A Two single subcarriers after including 42 dB losses, B Two single subcarriers after including 42 dB losses and changing the input of laser to 15 dB

Full size image

4 Conclusion

In this paper, we have developed and demonstrated a high linear analogue photonic link where all IMDs and SOH have been eliminated completely, by deploying unique system architecture which consisting of 6 RF shifters, 2 D-DPMZMs and 2 balance photodetectors. The proposed analog photonic link configuration which exhibits significant performance is easy to implement in practice (Zou et al. 2016). We have demonstrated that IMDs and SOH distortion products can be completely eliminated, which is a challenging task to achieve due to the fact that if signals are very close to each other, it will be very difficult to filter SOH by using various filtering techniques. We have demonstrated that the system SFDR is only limited by TOH distortions which are far apart from fundamental signal and can easily be filter by using low electronic filters. We also have benchmarked the developed mathematical model and system simulations, and it has been confirmed that the mathematical model and the simulation results match very well, confirming that the proposed system can be implemented in practise. Additionally, we have also demonstrated the SFDR of 120.5 dB.Hz1/2.