Coded cooperation for combating interference in mixed RF/FSO cooperative relays

Abstract

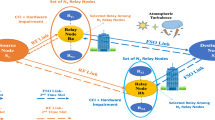
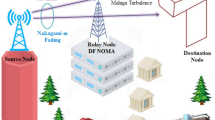
In this research work, coded cooperation protocol has been opted for combating impact of interference on a combined network of radio frequency (RF) and free space optical (FSO) systems called the mixed RF/FSO relaying system. The fading on the RF link has been considered to follow $\alpha -\mu$ distribution, whereas the atmospheric turbulence on the FSO link has been considered to follow double generalized Gamma turbulence model. With a purpose of introducing practicality to the system, it is considered that the relay node operates in the vicinity of multiple co-channel interferers. For the proposed system model, closed-form expressions for outage probability and ergodic capacity have been derived. The exact analysis for outage probability has been taken forward to derive asymptotic expression in terms of elementary functions. The findings of the research work suggest that coded cooperation can be utilized for combating the impact of interference at the relay node. Importantly, for mixed RF/FSO transmissions, coded cooperation outperforms decode-and-forward relaying strategy for the considered system model.

Appendix

A. Derivation of Eq. ( 15 )

In this section, the derivation steps of of Eq. (15) are elaborated. Noting the fact that from (14) and (6), it can be formulated as

$$\begin{aligned} \text {Pr}\Big [ \gamma _{{FSO}} < \varPsi (x) \Big ] = \int _{0}^{2^{\frac{R}{1-k}}} \int _{0}^{\varPsi (x)} f_{\gamma _{{sd}}}(x) f_{\gamma _{{FSO}}}(z) dx dz \end{aligned}$$

(34a)

$$\begin{aligned} = \int _{0}^{2^{\frac{R}{1-k}}} f_{\gamma _{{sd}}}(x) {\mathcal {A}}_1 \text {G}_{r+1, n+1}^{n, 1}\left[ {\mathcal {A}}_2 \left( \frac{\varPsi (x)}{\mu _r} \right) ^{y} \vert \begin{array}{c} 1,\phi _3 \\ \phi _4,0 \end{array} \right] dx \end{aligned}$$

(34b)

$$\begin{aligned} =\int _{0}^{2^{\frac{R}{1-k}}} f_{\gamma _{{sd}}}(x) {\mathcal {A}}_1 \text {G}_{n+1, r+1}^{1, n}\left[ \left( \frac{\mu _r}{{\mathcal {A}}_2}\right) ^y \frac{x^{\frac{yk}{1-k}}}{2^{\frac{yR}{1-k}}} \vert \begin{array}{c} \phi _5, 1 \\ 0, \phi _6 \end{array} \right] dx \end{aligned}$$

(34c)

With the aid of Wolfram (2010), the Meijer-G can be expressed in terms of complex integral as

$$\begin{aligned}\text { G}^{1,n}_{n+1,r+1} \left. \Big [ \left( \frac{\mu _r}{{\mathcal {A}}_2}\right) ^y \frac{x^{\frac{yk}{1-k}}}{2^{\frac{yR}{1-k}}} \vert \right. {\begin{matrix} \phi _5, 1 \\ 0, \phi _6 \end{matrix}}\Big ] = \frac{1}{2 \pi i} \int _{L_2} \left\{ \left( \frac{\mu _r}{{\mathcal {A}}_2}\right) ^y \right\} ^{(-s_2)} \bigg ({\frac{1}{2^{\frac{yR}{1-k}}}}\bigg )^{-s_2}{x^{\frac{-s_2 yk}{1-k}}} \varTheta (s_2) ds_2 \end{aligned}$$

(35)

Similarly, $f_{\gamma _{{sd}}}(x)$ can be expressed as

$$f_{{\gamma _{{sd}} }} (x) = {\mathcal{B}}_{{1,sd}} x^{{\frac{{\alpha _{{sd}} \mu _{{sd}} }}{2} - 1}} {\text{ }}G_{{0,1}}^{{1,0}} \left. {\left[ {{\mathcal{B}}_{{2,sd}} x^{{\frac{{\alpha _{{sd}} }}{2}}} {\text{ }}\left| {_{0}^{ - } } \right.} \right.} \right]$$

(36)

From (35), (36) and (34), it can be established that

$$\begin{aligned}\text {Pr}\Big [ \gamma _{{FSO}} \Psi (x) \Big ] =& {\mathcal {A}}_1 {\mathcal {B}}_{1, sd} \frac{1}{(2 \pi i)^2} \int _{L_1}\int _{L_2} \left( \frac{\mu _r}{{\mathcal {A}}_2}\right) ^{(-ys_2)} \bigg ({\frac{1}{2^{\frac{yR}{1-k}}}}\bigg )^{-s_2} \Theta (s_2) \Gamma (s_1) ({\mathcal {B}}_{2, sd})^{-s_1} \nonumber \\&\quad\times \int _{0}^{2^{\frac{R}{1-k}}} {x^{\frac{\alpha _{sd} \mu _{sd}}{2}-\frac{s_1\alpha _{sd}}{2}-\frac{s_2 yk}{1-k}-1}} dx \end{aligned}$$

(37)

The above expression can be simplified as

$$\begin{aligned}&\text {Pr}\Big [ \gamma _{{FSO}} < \varPsi (x) \Big ] = {\mathcal {A}}_1 {\mathcal {B}}_{1, sd} \frac{1}{(2 \pi i)^2} \int _{L_1}\int _{L_2} \left\{ \left( \frac{\mu _r}{{\mathcal {A}}_2}\right) ^y \right\} ^{(-s_2)} \bigg ({\frac{1}{2^{\frac{yR}{1-k}}}}\bigg )^{-s_2} \varTheta (s_2) \varGamma (s_1) ({\mathcal {B}}_{2, sd})^{-s_1} \nonumber \\&\times (2^{\frac{R}{1-k} ({\frac{\alpha _{sd} \mu _{sd}}{2}-\frac{s_1\alpha _{sd}}{2}-\frac{s_2 yk}{1-k}})}) \frac{\Gamma (\frac{\alpha _{sd} \mu _{sd}}{2}-\frac{s_1\alpha _{sd}}{2}-\frac{s_2 yk}{1-k}+1)}{\Gamma (\frac{\alpha _{sd} \mu _{sd}}{2}-\frac{s_1\alpha _{sd}}{2}-\frac{s_2 yk}{1-k})} \end{aligned}$$

(38)

Comparing the Mellin Barnes type double complex contour integral with [Mittal and Gupta (1972), Eq. (1.1)], the closed-form expression in (18) can be obtained to complete the proof.

B. Derivation of Eq. ( 20 )

Using the definition of Fox’s H-function in [Mittal and Gupta (1972), Eq. (1.1)], we have

$$\begin{aligned}\text {H}_{{\mathbf {x}}_2}^{{\mathbf {x}}_1}\left( \begin{array}{c} \phi _5 \\ \phi _6 \end{array}\vert \begin{array}{c} \underline{\,\,\,}\\ (0, 1)\\ \end{array}\vert \begin{array}{c} (1,1), (\phi _3, [1]_{\text {len}(\phi _3)})\\ (\phi _4, [1]_{\text {len}(\phi _3)}),(0,1) \\ \end{array}\vert {\mathcal {B}}_{6, sd},{\mathcal {A}}_3 \right) = &\frac{1}{(2\pi i)^2} \int _{L_1} \int _{L_2} \frac{\Gamma \left( 1+\frac{\alpha _{sd}\mu _{sd}}{2}-\frac{\alpha _{sd}}{2}s_1-\frac{y\kappa }{1-\kappa }s_2 \right) }{\Gamma \left( \frac{\alpha _{sd}\mu _{sd}}{2}-\frac{\alpha _{sd}}{2}s_1-\frac{y\kappa }{1-\kappa }s_2 \right) }\nonumber \\&\times \Gamma (s_1)\varTheta (s_2) \big ({\mathcal {B}}_{6, sd}\big )^{-s_1} \big ({\mathcal {A}}_3\big )^{-s_2} ds_1 ds_2 \end{aligned}$$

(39)

Now, consider the following complex integral

$$\begin{aligned} {\mathbf {h}}_1&= \frac{1}{2 \pi i} \int _{L_1} \frac{\Gamma \left( 1+\frac{\alpha _{sd}\mu _{sd}}{2}-\frac{\alpha _{sd}}{2}s_1-\frac{y\kappa }{1-\kappa }s_2 \right) }{\Gamma \left( \frac{\alpha _{sd}\mu _{sd}}{2}-\frac{\alpha _{sd}}{2}s_1-\frac{y\kappa }{1-\kappa }s_2 \right) } \Gamma (s_1) \big ({\mathcal {B}}_{6, sd}\big )^{-s_1} ds_1 \end{aligned}$$

(40)

With the aid of [Kilbas (2004), Eq. (1.2), (1.3), (1.132)], ${\mathbf {h}}_1$ can be expressed as follows

$$\begin{aligned}&{\mathbf {h}}_1 = \Big (\frac{\alpha _{sd} \mu _{sd}}{2}-\frac{y\kappa }{1-\kappa }s_2\Big ) {}_1\text {F}_1(1+\frac{\alpha _{sd} \mu _{sd}}{2}-\frac{y\kappa }{1-\kappa }s_2: \frac{\alpha _{sd} \mu _{sd}}{2}-\frac{y\kappa }{1-\kappa }s_2:-{\mathcal {B}}_{6, sd}) \end{aligned}$$

(41)

This completes the proof for derivation of (20).