Skip to main content
SpringerLink
Log in

Analyzing the multilayer metamaterial waveguide structure with the Kerr-type nonlinear cladding

  • Published:
Optical and Quantum Electronics Aims and scope Submit manuscript

Abstract

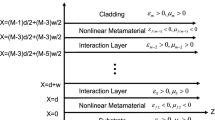
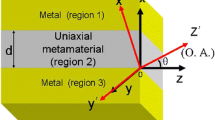
A general method for analyzing the multilayer metamaterial optical waveguides with the Kerr-type nonlinear cladding was proposed. To prove the accuracy of the proposed general method, a degenerated example was introduced. The analytical and numerical results show excellent agreement. The similar process can also be used to analyze TM waves propagating in the multilayer metamaterial waveguide structure with the Kerr-type nonlinear cladding.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  • Aghaie, K.Z., Shahabadi, M.: multiple-scale analysis of plane wave refraction at a dielectric slab with kerr-type nonlinearity. Prog. Electricmagn. Res. 56, 81–92 (2006)

    Article  Google Scholar 

  • Akhmediev, N., Ankiewicz, A.: Spatial soliton X-junction and couplers. Opt. Commun. 100, 186–192 (1993)

    Article  ADS  MATH  Google Scholar 

  • Al-Naib, I.A.I., Jansen, C., Koch, M.: Single metal layer CPW metamaterial band-pass flter. Prog. Electromagn. Res. Lett. 17, 153–161 (2010)

    Article  Google Scholar 

  • Awad, M., Nagel, M., Kurz, H.: Negative-index metamaterial with polymer-embedded wire-pair structures at terahertz frequencies. Opt. Lett. 33, 2683–2685 (2008)

    Article  ADS  Google Scholar 

  • Castaldi, G., Gallina, I., Galdi, V., Alú, A., Engheta, N.: Cloak/anti-cloak interactions. Opt. Express 17, 3101–3114 (2009)

    Article  ADS  MATH  Google Scholar 

  • Chang, W.C., Liu, S.F., Wang, W.S.: Novel photonic device using nonlinear corner-bend structure. Electron. Lett. 27, 2190–2192 (1991)

    Article  Google Scholar 

  • Darmanyan, S.A., Nevière, M., Zakhidov, A.A.: Nonlinear surface waves at the interfaces of left-handed electromagnetic media. Phys. Rev. E (2005). doi:10.1103/PhysRevE.72.036615

  • Doer, C.R., Kogelnik, H.: Dielectric waveguide theory. J. Lightwave Technol. 26, 1176–1187 (2008)

    Article  ADS  Google Scholar 

  • Dolling, G., Wegener, M., Soukoulis, C.M., Linden, S.: Negative-index metamaterial at 780 nm wavelength. Opt. Lett. 32, 53–55 (2007)

    Article  ADS  Google Scholar 

  • Duan, Z.Y., Wu, B.I., Xi, S., Chen, H., Chen, M.: Research progress in reversed Cherenkov radiation in double-negative metamaterials. Prog. Electromagn. Res. 90, 75–87 (2009)

    Article  Google Scholar 

  • Gong, Y., Wang, G.: Superficial tumor hyperthermia with flat left-handed metamaterial lens. Prog. Electromagn. Res. 98, 389–405 (2009)

    Article  Google Scholar 

  • Haruna, M., Koyama, J.: Electrooptic branching waveguide switches and their application to 1 × 4 optical switching networks. J. Lightwave Technol. 1, 223–227 (1983)

    Article  ADS  Google Scholar 

  • He, J., He, Y., Hong, Z.: Backward coupling o modes in a left-handed met material tapered waveguide. IEEE Microw. Wirel. Compon. Lett. 20, 378–380 (2010)

    Article  Google Scholar 

  • Huang, M.D., Tan, S.Y.: Efficient electrically small prolate spheroidal antennas coated with a shell of double-negative metamaterials. Prog. Electromagn. Res. 82, 241–255 (2008)

    Article  Google Scholar 

  • Hwang, R.-B., Liu, H.-W., Chin, C.-Y.: A metamaterial-based E-plane horn antenna. Prog. Electromagn. Res. 93, 275–289 (2009)

    Article  Google Scholar 

  • Kaman, V., Zheng, X., Yuan, S., Klingshirn, J., Pusarla, C., Helkey, R.J., Jerphagnon, O., Bowers, J.E.: A 32 × 10 Gb/s DWDM metropolitan network demonstration using wavelength-selective photonic cross-connects and narrow-band EDFAs. IEEE Photon. Technol. Lett. 17, 1977–1979 (2005)

    Article  ADS  Google Scholar 

  • Kim, C.K., Jeong, J.M., Chang, H.: All-optical logic functions in a bent nonlinear Y-junction waveguide. Jpn. J. Appl. Phys. 37, 832–836 (1998)

    Article  ADS  Google Scholar 

  • Kuo, C.W., Chen, S.Y., Wu, Y.D., Chen, M.H.: Analyzing the multilayer optical planar waveguides with double-negative metamaterial. Prog. Electricmagn. Res. 110, 163–178 (2010)

    Article  Google Scholar 

  • Ma, J.G., wolff, I.: Propagation characteristics of TE-wave guided by thin films bounded by nonlinear media. IEEE Trans. Microw. Theory Tech. 43, 790–795 (1995)

    Article  ADS  Google Scholar 

  • Ma, J.G., Wolff, I.: TE wave properties of slab dielectric guide bounded by nonlinear non-Kerr-like media. IEEE Trans. Microw. Theory Tech. 44, 730–738 (1996)

    Article  ADS  Google Scholar 

  • Manapati, M.B., Kshetrimayum, R.S.: SAR reduction in human head from mobile phone radiation using single negative metamaterials. J. Electromagn. Waves Appl. 23(10), 1385–1395 (2009)

    Article  Google Scholar 

  • Micallef, R.W., Kivshar, Y.S., Love, K.D.: All-optical switching and beam self-focusing in nonlinear single-mode Y-splitters. Electron. Lett. 33, 80–82 (1997)

    Article  Google Scholar 

  • Mihalache, D., Bertolotti, M., Sibilia, C.: Nonlinear wave propagation in planar structures. In: Wolf, E. (ed.) Progress in Optics, Vol. 27, pp. 227–313. North Holland, Amsterdam (1989)

    Chapter  Google Scholar 

  • Milonni, P.W., Maclay, G.J.: Quantized-field description of light negative-index media. Opt. Commun. 228, 161–165 (2003)

    Article  ADS  Google Scholar 

  • Mirza, I.O., Sabas, J.N., Shi, S., Prather, D.W.: Experimental demonstration of metamaterial based phase modulation. Prog. Electromagn. Res. 93, 1–12 (2009)

    Article  Google Scholar 

  • Pollock, J.G., Iyer, A.K.: Below-cutoff propagation in metamaterial-lined circular waveguides. IEEE Trans. Microw. Theory Tech. 61, 3169–3178 (2013)

    Article  ADS  Google Scholar 

  • Sabah, C., Uckun, S.: Multilayer system of Lorentz/drude type metamaterials with dielectric slabs and its application to electromagnetic lters. Prog. Electromagn. Res. 91, 349–364 (2009)

    Article  Google Scholar 

  • Sammut, R.A., Li, Q.Y., Pask, C.: Variational approximations and mode stability in planar nonlinear waveguides. J. Opt. Soc. Am. B 9, 884–890 (1992)

    Article  ADS  Google Scholar 

  • Seaton, C.T., Mai, X., Stegeman, G.I., Winful, H.G.: Nonlinear guided wave applications. Opt. Eng. 24, 593–599 (1985a)

    Article  ADS  Google Scholar 

  • Seaton, C.T., Valera, J.D., Shoemaker, R.L., Stegeman, G.I., Chilwell, J.T., Smith, D.: Calculations of nonlinear TE waves guided by thin dielectric films bounded by nonlinear media. IEEE J. Quantum Electron. 21, 774–783 (1985b)

    Article  ADS  Google Scholar 

  • Shadrivov, I.V., Sukhorukov, A.A., Kivshar, Y.S.: Guided modes in negative-refractive-index waveguides. Phys. Rev. E (2003). doi:10.1103/PhysRevE.67.057602

    Article  ADS  Google Scholar 

  • Shadrivov, I.V., Sukhorukov, A.A., Kivshar, Y.S., Zharov, A.A., Boardman, A.D., Egan, P.: Nonlinear surface waves in left-handed materials. Phys. Rev. E (2004). doi:10.1103/PhysRevE.69.016617

  • Shelby, R.A., Smith, D.R., Schultz, S.: Experimental verification of a negative index of refraction. Science 292(5514), 77–79 (2001)

    Article  ADS  Google Scholar 

  • Shen, M., Ruan, L., Chen, X.: Guided modes near the dirac point in negative-zero-positive index metamaterial waveguide. Opt. Express 18, 12779–12787 (2010)

    Article  ADS  Google Scholar 

  • Si, L.-M., Lv, X.: CPW-FED multi-band omni-directional planar microstrip antenna using composite metamaterial resonators for wireless communications. Prog. Electromagn. Res. 83, 133–146 (2008)

    Article  Google Scholar 

  • Stegeman, G.I., Seaton, C.T., Chilwell, J., Smith, S.D.: Nonlinear waves guided by thin films. Appl. Phys. Lett. 44, 830–832 (1984)

    Article  ADS  Google Scholar 

  • Stegeman, G.I., Wright, E.M., Finlayson, N., Zanoni, R., Seaton, C.T.: Third order nonlinear integrated optics. J. Lightwave Technol. 6, 953–970 (1988)

    Article  ADS  Google Scholar 

  • Vach, H., Stegeman, G.I., Seaton, C.T., Khoo, I.C.: Experimental observation of nonlinear guided waves. Opt. Lett. 9, 238–240 (1984)

    Article  ADS  Google Scholar 

  • Valera, J.D., Svensson, B., Seaton, C.T., Stegeman, G.I.: Bistability and switching in thin film waveguides with liquid crystal cladding. Appl. Phys. Lett. 48, 573–574 (1986)

    Article  ADS  Google Scholar 

  • Veselago, V.G.: The electrodynamics of substances with simultaneously negative values of ε and µ. Sov. Phys. Usp. 10(4), 509–514 (1968)

    Article  ADS  Google Scholar 

  • Wa, P.L.K., Robson, P.N., David, J.P.R., Hill, G., Mistry, P., Pate, M.A., Roberts, J.S.: All-optical switching effects in a passive GaAs/GaAlAs multiple-quantum-well waveguide resonator. Electron. Lett. 22, 1129–1130 (1986)

    Article  Google Scholar 

  • Wang, M.-Y., Xu, J., Wu, J., Wei, B., Li, H.-L., Xu, T., Ge, D.-B.: FDTD study on wave propagation in layered structures with biaxial anisotropic metamaterials. Prog. Electromagn. Res. 81, 253–265 (2008)

    Article  Google Scholar 

  • Wu, W.-Y., Lai, A., Kuo, C.W., Leong, K.M.K.H., Itoh, T.: Efficient FDTD method for analysis of mushroom-structure based left-handed materials. IET Microw. Antennas Propag. 1, 100–107 (2007a)

    Article  Google Scholar 

  • Wu, Y.D., Huang, M.L., Chen, M.H., Tasy, R.Z.: All-optical switch based on the local nonlinear Mach-Zehnder interferometer. Opt. Express 15, 9883–9892 (2007b)

    Article  ADS  Google Scholar 

  • Wu, Y.D., Shih, T.T., Chen, M.H.: New all-optical logic gates based on the local nonlinear Mach-Zehnder interferometer. Opt. Express 16, 248–257 (2008)

    Article  ADS  Google Scholar 

  • Xi, S., Chen, H., Wu, B.I., Kong, J.A.: Experimental confirmation of guidance properties using planar anisotropic left-handed metamaterial slabs based on S-ring resonators. Prog. Electromagn. Res. 84, 279–287 (2008)

    Article  Google Scholar 

  • Xiang, Y., Dai, X., Wen, S., Fan, D.: Review of nonlinear optics in metamaterials”. In: PIERS Proceedings, pp. 925—962. Hangzhou, China, (2008)

  • Yu, G.X., Cui, T.-J., Jiang, W.X., Yang, X.M., Cheng, Q., Hao, Y.: Transformation of different kinds of electromagnetic waves using metamaterials. J. Electromagn. WavesAppl. 23(5–6), 583–592 (2009)

    Article  Google Scholar 

  • Zhou, H., Pei, Z., Qu, S., Zhang, S., Wang, J., Li, Q., Xu, Z.: A planar zero-index metamaterial for directive emission. J. Electromagn. Waves Appl. 23, 953–962 (2009)

    Article  Google Scholar 

  • Ziolkowski, R.W.: Superluminal transmission of information through an electromagnetic metamaterial. Phys. Rev. E (2001). doi:10.1103/PhysRevE.63.046604

  • Ziolkowski, R.W., Heyman, E.: Wave propagation in media having negative permittivity and permeability. Phys. Rev. E (2001). doi:10.1103/PhysRevE.64.056625

  • Ziolkowski, R.W., Kipple, A.D.: Causality and double-negative metamaterials. Phys. Rev. E (2003). doi:10.1103/PhysRevE.68.026615

Download references

Author information

Authors and Affiliations

  1. Department of Electronic Engineering, National Kaohsiung University of Applied Sciences, Kaohsiung, 807, Taiwan, ROC

    Yaw-Dong Wu & Ming-Hsiung Cheng

Authors
  1. Yaw-Dong Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ming-Hsiung Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yaw-Dong Wu.

Appendix

Appendix

The constants \({\text{A}}_{\text{f}} (n)\), \({\text{A}}_{\text{s}}\), \({\text{A}}_{\text{i}} (n)\), \({\text{X}}_{\text{f}} (n)\), \({\text{X}}_{\text{i}} (n)\) can be expressed as follows:

$${\text{x}}_{\text{f}} ({\text{n}} + 1) = \frac{{ - ({\text{n}} + 1)}}{2}{\text{d}}_{\text{f}} - \frac{\text{n}}{2}{\text{d}}_{\text{i}} + \frac{1}{{{\text{k}}_{ 0} {\text{q}}_{\text{f}} }}{ \tan }^{ - 1} \left( {\frac{{\mu_{f} }}{{\mu_{s} }}\frac{{{\text{q}}_{\text{s}} {\kern 1pt} }}{{{\text{q}}_{\text{f}} }}} \right)$$
(21)
$${\text{x}}_{\text{f}} ({\text{n}} + 1) = \frac{{ - ({\text{n}} + 1)}}{2}{\text{d}}_{\text{f}} - \frac{\text{n}}{2}{\text{d}}_{\text{i}} + \frac{1}{{{\text{k}}_{ 0} {\text{Q}}_{\text{f}} }}{ \tanh }^{ - 1} \left( {\frac{{\mu_{s} }}{{\mu_{f} }}\frac{{{\text{ - Q}}_{\text{f}} {\kern 1pt} }}{{{\text{q}}_{\text{s}} }}} \right)$$
(22)
$${\text{A}}_{\text{f}} {\kern 1pt} (1) = \frac{{{\text{E}}_{\text{c}} }}{{\cos \left[ {{\text{k}}_{ 0} {\text{q}}_{\text{f}} \left( {\frac{{{\text{n}} + 1}}{2}{\text{d}}_{\text{f}} + \frac{\text{n}}{2}{\text{d}}_{\text{i}} - x_{\text{f}} (1)} \right)} \right]}}$$
(23)
$${\text{A}}_{\text{f}} (1) = \frac{{{\text{E}}_{\text{c}} }}{{\sinh \left[ {{\text{k}}_{ 0} {\text{Q}}_{\text{f}} \left( {\frac{{{\text{n}} + 1}}{ 2}{\text{d}}_{\text{f}} + \frac{\text{n}}{2}{\text{d}}_{\text{i}} - x_{\text{f}} ( 1 )} \right)} \right]}}$$
(24)
$${\text{A}}_{\text{f}} ({\text{n}} + 1) = {\text{A}}_{\text{i}} ({\text{n}})\frac{{\cosh \left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left( {\frac{{{\text{n}} - 1}}{2}{\text{d}}_{\text{f}} + \frac{\text{n}}{2}{\text{d}}_{\text{i}} + {\text{x}}_{i} ({\text{n}})} \right)} \right]}}{{\cos \left[ {{\text{k}}_{ 0} {\text{q}}_{\text{f}} \left( {\frac{{{\text{n}} - 1}}{2}{\text{d}}_{\text{f}} + \frac{\text{n}}{2}{\text{d}}_{\text{i}} + {\text{x}}_{\text{f}} ({\text{n}} + 1)} \right)} \right]}}{\kern 1pt}$$
(25)
$${\text{A}}_{\text{f}} ({\text{n}} + 1) = - {\text{A}}_{\text{i}} ({\text{n}})\frac{{\cosh \left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left( {\frac{{{\text{n}} - 1}}{2}{\text{d}}_{\text{f}} + \frac{\text{n}}{2}{\text{d}}_{\text{i}} + {\text{x}}_{\text{i}} ({\text{n}})} \right)} \right]}}{{\sinh \left[ {{\text{k}}_{ 0} {\text{Q}}_{\text{f}} \left( {\frac{{{\text{n}} - 1}}{2}{\text{d}}_{\text{f}} + \frac{\text{n}}{2}{\text{d}}_{\text{i}} + {\text{x}}_{\text{f}} ({\text{n}} + 1)} \right)} \right]}}{\kern 1pt}$$
(26)
$${\text{A}}_{\text{i}} (1) = {\text{A}}_{\text{f}} ( 1 )\frac{{{\kern 1pt} \cos \left[ {{\text{k}}_{ 0} {\text{q}}_{\text{f}} \left( {\frac{{{\text{n}} - 1}}{ 2}{\text{d}}_{\text{f}} + \frac{\text{n}}{2}{\text{d}}_{\text{i}} - {\text{x}}_{\text{f}} ( 1 )} \right)} \right]}}{{\cosh \left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left( {\frac{{{\text{n}} - 1}}{ 2}{\text{d}}_{\text{f}} + \frac{\text{n}}{2}{\text{d}}_{\text{i}} - {\text{x}}_{\text{i}} ( 1 )} \right)} \right]}}$$
(27)
$${\text{A}}_{\text{i}} (1) = {\text{A}}_{\text{f}} ( 1 )\frac{{\sinh \left[ {{\text{k}}_{ 0} {\text{Q}}_{\text{f}} \left( {\frac{{{\text{n}} - 1}}{ 2}{\text{d}}_{\text{f}} + \frac{\text{n}}{2}{\text{d}}_{\text{i}} - {\text{x}}_{\text{f}} ( 1 )} \right)} \right]}}{{\cosh \left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left( {\frac{{{\text{n}} - 1}}{ 2}{\text{d}}_{\text{f}} + \frac{\text{n}}{2}{\text{d}}_{\text{i}} - {\text{x}}_{\text{i}} ( 1 )} \right)} \right]}}$$
(28)
$${\text{A}}_{\text{s}} = {\text{A}}_{\text{f}} ( {\text{n}} + 1 ) {\text{cos}}\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{f}} \left( {\frac{{{\text{n}} + 1}}{ 2}{\text{d}}_{\text{f}} + \frac{\text{n}}{ 2}{\text{d}}_{\text{i}} + {\text{x}}_{\text{f}} ( {\text{n}} + 1 )} \right)} \right] \cdot { \exp }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{f}} \left( {\frac{{{\text{n}} + 1}}{ 2}{\text{d}}_{\text{f}} + \frac{\text{n}}{ 2}{\text{d}}_{\text{i}} } \right)} \right]$$
(29)
$${\text{A}}_{\text{s}} = {\text{A}}_{\text{f}} ( {\text{n}} + 1 ) {\text{sinh}}\left[ {{\text{k}}_{ 0} {\text{Q}}_{\text{f}} \left( {\frac{{{\text{n}} + 1}}{ 2}{\text{d}}_{\text{f}} + \frac{\text{n}}{ 2}{\text{d}}_{\text{i}} + {\text{x}}_{\text{f}} ( {\text{n}} + 1 )} \right)} \right] \cdot { \exp }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{f}} \left( {\frac{{{\text{n}} + 1}}{ 2}{\text{d}}_{\text{f}} + \frac{\text{n}}{ 2}{\text{d}}_{\text{i}} } \right)} \right]$$
(30)

For \({\mathbf{0}} \le {\mathbf{p}} \le {\mathbf{n}} - {\mathbf{1,n}} - {\mathbf{p}} \ne {\mathbf{1}}\)

$${\text{A}}_{\text{f}} ( {\text{n}} - {\text{p)}} = {\text{A}}_{\text{i}} ( {\text{n}} - {\text{p}} - 1 )\frac{{{ \cosh }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left( {\frac{{{\text{n}} - 3}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{n}} - 2}}{ 2} - {\text{p)d}}_{\text{i}} + {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}} - 1} \right)} \right]}}{{{\text{cos[k}}_{ 0} {\text{q}}_{\text{f}} \left( {\left( {\frac{{{\text{n}} - 3}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{n}} - 2}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} + {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}}} \right) ]}}$$
(31)
$${\text{A}}_{\text{f}} ( {\text{n}} - {\text{p)}} = - {\text{A}}_{\text{i}} ( {\text{n}} - {\text{p}} - 1 )\frac{{{ \cosh }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left( {\frac{{{\text{n}} - 3}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{n}} - 2}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} + {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p}} - 1 ) )} \right]}}{{{ \sinh }\left[ {{\text{k}}_{ 0} {\text{Q}}_{\text{f}} \left( {\left( {\frac{{{\text{n}} - 3}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{n}} - 2}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} + {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}}} \right)} \right]}}$$
(32)
$${\text{A}}_{\text{i}} ({\text{n}} - {\text{p}}) = {\text{A}}_{\text{f}} ({\text{n}} - {\text{p}})\frac{{\cos \left[ {{\text{k}}_{ 0} {\text{q}}_{\text{f}} \left( {\left( {\frac{{{\text{n}} - 1}}{2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{n}} - 2}}{2} - {\text{p}}} \right){\text{d}}_{\text{i}} + {\text{x}}_{\text{f}} ({\text{n}} - {\text{p}})} \right)} \right]}}{{\cosh \left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left( {\left( {\frac{{{\text{n}} - 1}}{2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{n}} - 2}}{2} - {\text{p}}} \right){\text{d}}_{\text{i}} + {\text{x}}_{\text{i}} ({\text{n}} - {\text{p}})} \right)} \right]}}$$
(33)
$${\text{A}}_{\text{i}} ( {\text{n}} - {\text{p)}} = - {\text{A}}_{\text{f}} ( {\text{n}} - {\text{p)}}\frac{{{ \sinh }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{f}} \left( {\left( {\frac{{{\text{n}} - 1}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{n}} - 2}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} + {\text{x}}_{\text{f}} ( {\text{n}} - {\text{p)}}} \right)} \right]}}{{{ \cosh }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left( {\left( {\frac{{{\text{n}} - 1}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{n}} - 2}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} + {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}}} \right)} \right]}}$$
(34)

Part I:n = odd

$${\mathbf{0}} \le {\mathbf{p}} \le ({\mathbf{n}} - {\mathbf{3)/2 }}$$
$$\begin{aligned} {\text{x}}_{\text{f}} ({\text{n}} - {\text{p}}) &= \left( {\frac{{ - ({\text{n}} - 1)}}{2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{ - ({\text{n}} - 2)}}{2} + {\text{p}}} \right){\text{d}}_{\text{i}} \\ & + \frac{{\tan^{ - 1} \left\{ {\frac{{\upmu_{f} }}{{\upmu_{i} }}\frac{{{\text{ - q}}_{\text{i}} }}{{{\text{q}}_{\text{f}} }}\tanh \left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left[ {\left( {\frac{{({\text{n}} - 1)}}{2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{n}} - 2}}{2} - {\text{p}}} \right){\text{d}}_{\text{i}} + {\text{x}}_{\text{i}} ({\text{n}} - {\text{p}})} \right]} \right]} \right\}}}{{k_{ 0} {\text{q}}_{\text{f}} }} \\ \end{aligned}$$
(35)
$$\begin{aligned} {\text{x}}_{\text{f}} ( {\text{n}} - {\text{p)}} = \left( {\frac{{ - ( {\text{n}} - 1 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{ - (n}} - 2 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{i}} \\ & \quad+ \frac{{{ \tanh }^{ - 1} \left\{ {\frac{{\upmu_{i} }}{{\upmu_{f} }}\frac{{{\text{Q}}_{\text{f}} }}{{{\text{q}}_{\text{i}} { \tanh }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left[ {\left( {\frac{{ ( {\text{n}} - 1 )}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{n}} - 2}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} + {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}}} \right]} \right]}}} \right\}}}{{{\text{k}}_{ 0} {\text{Q}}_{\text{f}} }} \\ \end{aligned}$$
(36)
$$\begin{aligned} {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}} &= \left( {\frac{{ - ( {\text{n}} - 1 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{\text{ - n}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{i}} \\ \quad + \frac{{{ \tanh }^{ - 1} \left\{ {\frac{{\upmu_{\text{i}} }}{{\upmu_{\text{f}} }}\frac{{{\text{ - q}}_{\text{f}} }}{{{\text{q}}_{\text{i}} }}{ \tan }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{f}} \left[ {\left( {\frac{{ ( {\text{n}} - 1 )}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{\text{n}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} + {\text{x}}_{\text{c}} ( {\text{n}} - {\text{p}} + 1 )} \right]} \right]} \right\}}}{{{\text{k}}_{ 0} {\text{q}}_{\text{i}} }} \\ \end{aligned}$$
(37)
$$\begin{aligned} {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}} & = \left( {\frac{{ - ( {\text{n}} - 1 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{\text{ - n}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{i}} \\ & \quad + \frac{{{ \tanh }^{ - 1} \left\{ {\frac{{\upmu_{\text{i}} }}{{\upmu_{\text{f}} }}\frac{{{\text{Q}}_{\text{f}} }}{{{\text{q}}_{\text{i}} { \tanh }\left[ {{\text{k}}_{ 0} {\text{Q}}_{\text{f}} \left[ {\left( {\frac{{ ( {\text{n}} - 1 )}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{\text{n}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} + {\text{x}}_{\text{f}} ( {\text{n}} - {\text{p}} + 1 )} \right]} \right]}}} \right\}}}{{{\text{k}}_{ 0} {\text{q}}_{\text{i}} }} \\ \end{aligned}$$
(38)
$${\mathbf{(n}} + {\mathbf{1)/2}} \le {\mathbf{p}} \le ({\mathbf{n}} - {\mathbf{1) }}$$
$$\begin{aligned} {\text{x}}_{\text{f}} ( {\text{n}} - {\text{p)}} & =\left( {\frac{{ - ( {\text{n}} - 1 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{ - (n}} - 2 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{i}} \\ & \quad + \frac{{{ \tan }^{ - 1} \left\{ {\frac{{{\text{ - q}}_{\text{i}} }}{{{\text{q}}_{\text{f}} }}{ \tanh }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left[ {{ - }\left( {\frac{{ ( {\text{n}} - 1 )}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} - \left( {\frac{{{\text{n}} - 2}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} - {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}}} \right]} \right]} \right\}}}{{{\text{k}}_{ 0} {\text{q}}_{\text{f}} }} \\ \end{aligned}$$
(39)
$$\begin{aligned} {\text{x}}_{\text{f}} ( {\text{n}} - {\text{p)}} & = \left( {\frac{{ - ( {\text{n}} - 1 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{ - (n}} - 2 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{i}} \\ & \quad + \frac{{{ \tanh }^{ - 1} \left\{ {\frac{{\upmu_{\text{i}} }}{{\upmu_{\text{f}} }}\frac{{{\text{Q}}_{\text{f}} }}{{{\text{q}}_{\text{i}} { \tanh }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left[ {{ - }\left( {\frac{{ ( {\text{n}} - 1 )}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} - \left( {\frac{{{\text{n}} - 2}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} - {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}}} \right]} \right]}}} \right\}}}{{{\text{k}}_{ 0} {\text{Q}}_{\text{f}} }} \\ \end{aligned}$$
(40)
$$\begin{aligned} {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}} & = \left( {\frac{{ - ( {\text{n}} - 1 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{\text{ - n}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{i}} \\ & - \frac{{{ \tanh }^{ - 1} \left\{ {\frac{{\upmu_{\text{i}} }}{{\upmu_{\text{f}} }}\frac{{{\text{ - q}}_{\text{f}} }}{{{\text{q}}_{\text{i}} }}{ \tan }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{f}} \left[ {{ - }\left( {\frac{{ ( {\text{n}} - 1 )}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} - \left( {\frac{\text{n}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} - {\text{x}}_{\text{f}} ( {\text{n}} - {\text{p}} + 1 )} \right]} \right]} \right\}}}{{{\text{k}}_{ 0} {\text{q}}_{\text{i}} }} \\ \end{aligned}$$
(41)
$$\begin{aligned} {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}} & = \left( {\frac{{ - ( {\text{n}} - 1 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{\text{ - n}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{i}} \\ & \quad - \frac{{{ \tanh }^{ - 1} \left\{ {\frac{{\upmu_{\text{i}} }}{{\upmu_{\text{f}} }}\frac{{{\text{Q}}_{\text{f}} }}{{{\text{q}}_{\text{i}} { \tanh }\left[ {{\text{k}}_{ 0} {\text{Q}}_{\text{f}} \left[ {{ - }\left( {\frac{{ ( {\text{n}} - 1 )}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} - \left( {\frac{\text{n}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} - {\text{x}}_{\text{f}} ( {\text{n}} - {\text{p}} + 1 )} \right]} \right]}}} \right\}}}{{{\text{k}}_{ 0} {\text{q}}_{\text{i}} }} \\ \end{aligned}$$
(42)

otherwise

$${\text{x}}_{\text{f}} \left( {\frac{{{\text{n}} + 1}}{ 2}} \right) = \frac{ 1}{ 2}{\text{d}}_{\text{i}} - \frac{{\tan^{ - 1} \left\{ {\frac{{\mu_{f} }}{{\mu_{i} }}\frac{{{\text{ - q}}_{\text{i}} }}{{{\text{q}}_{\text{f}} }}\tanh \left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left( {\frac{ 1}{ 2}{\text{d}}_{\text{i}} - {\text{x}}_{\text{i}} \left( {\frac{{{\text{n}} + 1}}{ 2}} \right)} \right)} \right]} \right\}}}{{{\text{k}}_{ 0} {\text{q}}_{\text{f}} }}$$
(43)
$${\text{x}}_{\text{f}} \left( {\frac{{{\text{n}} + 1}}{ 2}} \right) = \frac{ 1}{ 2}{\text{d}}_{\text{i}} - \frac{{\tanh^{ - 1} \left\{ {\frac{{\mu_{i} }}{{\mu_{f} }}\frac{{{\text{Q}}_{\text{f}} }}{{{\text{q}}_{\text{i}} \tanh \left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left( {\frac{ 1}{ 2}{\text{d}}_{\text{i}} - {\text{x}}_{\text{i}} \left( {\frac{{{\text{n}} + 1}}{ 2}} \right)} \right)} \right]}}} \right\}}}{{{\text{k}}_{ 0} {\text{Q}}_{\text{f}} }}$$
(44)
$${\text{x}}_{\text{i}} \left( {\frac{{{\text{n}} + 1}}{ 2}} \right) = \frac{ - 1}{ 2}{\text{d}}_{\text{i}} + \frac{{\tanh^{ - 1} \left\{ {\frac{{\mu_{i} }}{{\mu_{f} }}\frac{{{\text{ - q}}_{\text{f}} }}{{{\text{q}}_{\text{i}} }}\tan \left[ {{\text{k}}_{ 0} {\text{q}}_{\text{f}} \left( {\frac{ 1}{ 2}{\text{d}}_{\text{i}} + {\text{x}}_{\text{f}} \left( {\frac{{{\text{n}} + 3}}{ 2}} \right)} \right)} \right]} \right\}}}{{{\text{k}}_{ 0} {\text{q}}_{\text{i}} }}$$
(45)
$${\text{x}}_{\text{i}} \left(\frac{{{\text{n}} + 1}}{ 2}\right) = \frac{ - 1}{ 2}{\text{d}}_{\text{i}} + \frac{{\tanh^{ - 1} \left\{ {\frac{{\mu_{i} }}{{\mu_{f} }}\frac{{{\text{Q}}_{\text{f}} }}{{{\text{q}}_{\text{i}} \tanh [{\text{k}}_{ 0} {\text{Q}}_{\text{f}} (\frac{ 1}{ 2}{\text{d}}_{\text{i}} + {\text{x}}_{\text{f}} (\frac{{{\text{n}} + 3}}{ 2}) )]}}} \right\}}}{{{\text{k}}_{ 0} {\text{q}}_{\text{i}} }}$$
(46)

Part II:n = even

$${\mathbf{0}} \le {\mathbf{p}} \le ({\mathbf{n}} - {\mathbf{2)/2 }}$$
$$\begin{aligned} {\text{x}}_{\text{f}} ( {\text{n}} - {\text{p)}} &= \left( {\frac{{ - ( {\text{n}} - 1 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{ - (n}} - 2 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{i}} \\ & \quad + \frac{{{ \tan }^{ - 1} \left\{ {\frac{{\upmu_{\text{i}} }}{{\upmu_{\text{f}} }}\frac{{{\text{ - q}}_{\text{i}} }}{{{\text{q}}_{\text{f}} }}{ \tanh }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left[ {\left( {\frac{{ ( {\text{n}} - 1 )}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{n}} - 2}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} + {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}}} \right]} \right]} \right\}}}{{{\text{k}}_{ 0} {\text{q}}_{\text{f}} }} \\ \end{aligned}$$
(47)
$$\begin{aligned} {\text{x}}_{\text{f}} ( {\text{n}} - {\text{p)}} & = \left( {\frac{{ - ( {\text{n}} - 1 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{ - (n}} - 2 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{i}} \\ & \quad + \frac{{{ \tanh }^{ - 1} \left\{ {\frac{{\upmu_{\text{i}} }}{{\upmu_{\text{f}} }}\frac{{{\text{Q}}_{\text{f}} }}{{{\text{q}}_{\text{i}} { \tanh }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left[ {\left( {\frac{{ ( {\text{n}} - 1 )}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{n}} - 2}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} + {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}}} \right]} \right]}}} \right\}}}{{{\text{k}}_{ 0} {\text{Q}}_{\text{f}} }} \\ \end{aligned}$$
(48)
$$\begin{aligned} {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}} & = \left( {\frac{{ - ( {\text{n}} - 1 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{\text{ - n}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{i}} \\ & \quad + \frac{{{ \tanh }^{ - 1} \left\{ {\frac{{\upmu_{\text{i}} }}{{\upmu_{\text{f}} }}\frac{{{\text{ - q}}_{\text{f}} }}{{{\text{q}}_{\text{i}} }}{ \tan }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{f}} \left[ {\left( {\frac{{ ( {\text{n}} - 1 )}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{\text{n}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} + {\text{x}}_{\text{f}} ( {\text{n}} - {\text{p}} + 1 )} \right]} \right]} \right\}}}{{{\text{k}}_{ 0} {\text{q}}_{\text{i}} }} \\ \end{aligned}$$
(49)
$$\begin{aligned} {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}}& = \left( {\frac{{ - ( {\text{n}} - 1 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{\text{ - n}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{i}} \\ & \quad + \frac{{{ \tanh }^{ - 1} \left\{ {\frac{{\upmu_{\text{i}} }}{{\upmu_{\text{f}} }}\frac{{{\text{Q}}_{\text{f}} }}{{{\text{q}}_{\text{i}} { \tanh }\left[ {{\text{k}}_{ 0} {\text{Q}}_{\text{f}} \left( {\frac{{ ( {\text{n}} - 1 )}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{\text{n}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} + {\text{x}}_{\text{f}} ( {\text{n}} - {\text{p}} + 1 )} \right]}}} \right\}}}{{{\text{k}}_{ 0} {\text{q}}_{\text{i}} }} \\ \end{aligned}$$
(50)
$${\mathbf{n/2}} \le {\mathbf{p}} \le ({\mathbf{n}} - {\mathbf{1) }}$$
$$\begin{aligned} {\text{x}}_{\text{f}} ( {\text{n}} - {\text{p)}} & = \left( {\frac{{ - ( {\text{n}} - 1 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{ - (n}} - 2 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{i}} \\ & \quad - \frac{{{ \tan }^{ - 1} \left\{ {\frac{{\upmu_{\text{i}} }}{{\upmu_{\text{f}} }}\frac{{{\text{ - q}}_{\text{i}} }}{{{\text{q}}_{\text{f}} }}{ \tanh }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left[ {{ - }\left( {\frac{{ ( {\text{n}} - 1 )}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} - \left( {\frac{{{\text{n}} - 2}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} - {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}}} \right]} \right]} \right\}}}{{{\text{k}}_{ 0} {\text{q}}_{\text{f}} }} \\ \end{aligned}$$
(51)
$$\begin{aligned} {\text{x}}_{\text{f}} & = \left( {\frac{{ - ( {\text{n}} - 1 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{{{\text{ - (n}} - 2 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{i}} \hfill \\ & \quad - \frac{{{ \tanh }^{ - 1} \left\{ {\frac{{\upmu_{\text{i}} }}{{\upmu_{\text{f}} }}\frac{{{\text{Q}}_{\text{f}} }}{{{\text{q}}_{\text{i}} { \tanh }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{i}} \left[ {{ - }\left( {\frac{{ ( {\text{n}} - 1 )}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} - \left( {\frac{{{\text{n}} - 2}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} - {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}}} \right]} \right]}}} \right\}}}{{{\text{k}}_{ 0} {\text{Q}}_{\text{f}} }} \hfill \\ \end{aligned}$$
(52)
$$\begin{aligned} {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}} & = \left( {\frac{{ - ( {\text{n}} - 1 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{\text{ - n}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{i}} \\ & \quad - \frac{{{ \tanh }^{ - 1} \left\{ {\frac{{\upmu_{\text{i}} }}{{\upmu_{\text{f}} }}\frac{{{\text{ - q}}_{\text{f}} }}{{{\text{q}}_{\text{i}} }}{ \tan }\left[ {{\text{k}}_{ 0} {\text{q}}_{\text{f}} \left[ {{ - }\left( {\frac{{ ( {\text{n}} - 1 )}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} - \left( {\frac{\text{n}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} - {\text{x}}_{\text{f}} ( {\text{n}} - {\text{p}} + 1 )} \right]} \right]} \right\}}}{{{\text{k}}_{ 0} {\text{q}}_{\text{i}} }} \\ \end{aligned}$$
(53)
$$\begin{aligned} {\text{x}}_{\text{i}} ( {\text{n}} - {\text{p)}} & = \left( {\frac{{ - ( {\text{n}} - 1 )}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{f}} + \left( {\frac{\text{ - n}}{ 2} + {\text{p}}} \right){\text{d}}_{\text{i}} \\ & \quad - \frac{{{ \tanh }^{ - 1} \left\{ {\frac{{\upmu_{\text{i}} }}{{\upmu_{\text{f}} }}\frac{{{\text{Q}}_{\text{f}} }}{{{\text{q}}_{\text{i}} { \tanh }\left[ {{\text{k}}_{ 0} {\text{Q}}_{\text{f}} \left[ {{ - }\left( {\frac{{ ( {\text{n}} - 1 )}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{f}} - \left( {\frac{\text{n}}{ 2} - {\text{p}}} \right){\text{d}}_{\text{i}} - {\text{x}}_{\text{f}} ( {\text{n}} - {\text{p}} + 1 )} \right]} \right]}}} \right\}}}{{{\text{k}}_{ 0} {\text{q}}_{\text{i}} }} \\ \end{aligned}$$
(54)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, YD., Cheng, MH. Analyzing the multilayer metamaterial waveguide structure with the Kerr-type nonlinear cladding. Opt Quant Electron 49, 181 (2017). https://doi.org/10.1007/s11082-017-1016-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11082-017-1016-5

Keywords

Search

Navigation