Resonant modal conversion in a two-mode waveguide

Abstract

We characterize a system consisting of a two-mode waveguide coupled to a single-mode microring resonator possibly presenting a nonlinear response of Kerr type. By using the scattering parameter formalism extended to the multimode domain, we show that in the linear regime and for an ideally transparent medium, each resonance of the system can be exploited to perform complete even-to-odd (respectively, odd-to-even) modal conversion. Moreover, when the Kerr nonlinearity is effective, the microring enables a power-dependent modal switching mediated by phase bistability. Thanks to its mode-processing capabilities, this configuration is suitable to find application as a functional building-block in mode-division multiplexing (MDM) photonic integrated circuits.

Appendices

Appendix 1: Considerations on the choice of the modal basis

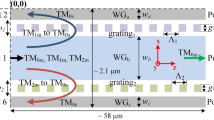
In Sect. 4, the matrix expression for the coupler has been obtained by treating the two-mode waveguide (TMWG) as a system of mutually coupled single-mode waveguides (SMWG), thus obtaining a description of the field evolutions in the fully single-mode basis $\left\{ e_1,e_2,e_3 \right\}$, where $e_n$ denotes the unit (normalized) vector associated to the mode propagating in the n-th single-mode channel. A possible alternative basis is the one using $\left\{ e_1,e_{even},e_{odd}\right\}$, in which $e_{even}$ (resp. $e_{odd}$) denotes the even (resp. odd) amplitudes of the modes in the two-mode waveguide (see Fig. 3). Within this alternative hybrid single/multi-mode framework, the evolution equation takes the following form:

$$\begin{aligned} i\frac{\partial }{{\partial z}}\left( {\begin{array}{c} {{F_1}}\\ {{F_{even}}}\\ {{F_{odd}}} \end{array}} \right) = \left( {\begin{array}{ccc} \beta &{}\quad {{\chi _{1e}}}&{}\quad {{\chi _{1o}}}\\ {{\chi _{1e}}}&{}\quad \beta _{even}&{}\quad 0\\ {{\chi _{1o}}}&{}\quad 0&{}\quad \beta _{odd} \end{array}} \right) \left( {\begin{array}{c} {{F_1}}\\ {{F_{even}}}\\ {{F_{odd}}} \end{array}} \right) , \end{aligned}$$

(29)

where $\beta$ denotes, as previously, the propagation constant of the upper SMWG, and $\beta _{even}$ (resp. $\beta _{odd}$) stands for the propagation constant of the even (resp. odd) mode in the lower TMWG. As far as coupling constants are concerned, we need an expression for both $\chi _{1e}$ (between mode 1 and mode even) and $\chi _{1o}$ (between mode 1 and mode odd). This means two degrees of freedom for a complete description of the coupler. Besides, thanks to their intrinsic orthogonality, no direct coupling between the even and odd modes needs to be accounted for.

On the other hand, within the framework exploited in Sect. 4, the TMWG is treated as a system of two mutually coupled SMWG interacting with the upper SMWG, the coupling being always limited to the nearest neighbour(s). For the sake of algebraic simplicity, the three SMWG are assumed identical, sharing therefore the same propagation constant $\beta$. The upper (resp. lower) coupling constant is denoted $\chi _a$ (resp. $\chi _b$). In this basis, according to Eq. (5):

$$\begin{aligned} i\frac{\partial }{{\partial z}}\left( {\begin{array}{c} {{F_1}}\\ {{F_2}}\\ {{F_3}} \end{array}} \right) = \left( {\begin{array}{ccc} \beta &{}\quad {{\chi _a}}&{}\quad 0\\ {{\chi _a}}&{}\quad \beta &{}\quad {{\chi _b}}\\ 0&{}\quad {{\chi _b}}&{}\quad \beta \end{array}} \right) \left( {\begin{array}{c} {{F_1}}\\ {{F_2}}\\ {{F_3}} \end{array}} \right) . \end{aligned}$$

(30)

The complex amplitudes of the modes can be transformed from one basis into the other by means of the following rotation matrices:

$$\begin{aligned} \left( {\begin{array}{c} {{F_1}}\\ {{F_{even}}}\\ {{F_{odd}}} \end{array}} \right) = \left( {\begin{array}{ccc} 1&{}0&{}0\\ 0&{}\quad \sqrt{2}/2&{}\quad \sqrt{2}/2\\ 0&{}\quad -\sqrt{2}/2&{}\quad \sqrt{2}/2 \end{array}} \right) \left( {\begin{array}{c} {{F_1}}\\ {{F_2}}\\ {{F_3}} \end{array}} \right) ,\;\;\; \left( {\begin{array}{c} {{F_1}}\\ {{F_2}}\\ {{F_3}} \end{array}} \right) = \left( {\begin{array}{ccc} 1 &{}0&{}0\\ 0&{}\quad \sqrt{2}/2 &{}\quad -\sqrt{2}/2 \\ 0&{}\quad \sqrt{2}/2 &{}\quad \sqrt{2}/2 \end{array}} \right) \left( {\begin{array}{c} {{F_1}}\\ {{F_{even}}}\\ {{F_{odd}}} \end{array}} \right) . \end{aligned}$$

(31)

As a result, we get eventually:

$$\begin{aligned} i\frac{\partial }{{\partial z}}\left( {\begin{array}{c} {{F_1}}\\ {{F_{even}}}\\ {{F_{odd}}} \end{array}} \right) = \left( {\begin{array}{ccc} \beta &{}\quad {{\chi _a}/\sqrt{2}}&{}\quad -{{\chi _a}/\sqrt{2}}\\ {{\chi _a}/\sqrt{2}}&{}\quad \beta +\chi _b&{}0\\ -{{\chi _a}/\sqrt{2}}&{}\quad 0&{}\quad \beta -\chi _b \end{array}} \right) \left( {\begin{array}{c} {{F_1}}\\ {{F_{even}}}\\ {{F_{odd}}} \end{array}} \right) . \end{aligned}$$

(32)

Equation (32) should be now compared with Eq. (30). Note that the three modes $\left\{ e_1,e_{even},e_{odd}\right\}$ do not propagate at the same velocity, and that the coupling between $e_1$ and $e_{even}$ has the same magnitude (but not the same sign) as that between $e_1$ and $e_{odd}$. Not only do we recover the (rather obvious) fact that $\beta _{even}=\beta +\chi _b$ and $\beta _{even}=\beta -\chi _b$: by identification, we also determine a compact expression for the coupling constants $\chi _{1e}=-\chi _{1o}=\chi _a/\sqrt{2}$. In other words, the approach dealing with single mode waveguides is simpler, as one less degree of freedom is required. Moreover, a multimode propagation problem looks more easily tractable and understandable in terms of coupled single-mode channels, thus giving an alternative picture with an immediate physical insight.

Appendix 2: Intersection of a Lorentzian function with a straight line

If the microring resonances are sharp enough to be assimilated to Lorentzian functions, then, with a suitable variable substitution, Eq. (26) can be recast into the following equivalent form:

$$\begin{aligned} \frac{1}{x^2+1}=\frac{x+a}{K}\Leftrightarrow \left( x^2+1\right) \left( x+a\right) =K, \end{aligned}$$

(33)

modelling the intersection of a Lorentzian curve with a straight line of horizontal intercept (anchor point) a and its inverse slope K, as depicted in Fig. 9.

Equation (33) is polynomial equation of the third-order, which is algebraically solvable by means of the Cardano’s formula, and whose roots are parametrized by a and K. By operating the substitutions: $b=(a/3)$, $z=x+b$, $p'=-b^2+\left( 1/3\right)$ and $q'=b^3+b-\left( K/2\right)$, Eq. (33) can be recast into its reduced cubic form:

$$\begin{aligned} z^3+3p'z+2q'=0, \end{aligned}$$

(34)

which allows to investigate the nature of the roots more easily. More specifically, Eq. (33) admits three real (physical) solutions only if the factor:

$$\begin{aligned} R=(p')^3+(q')^2=\left( K'\right) ^2-2K'b\left( b^2+1\right) +\frac{18b^2+1}{27},\quad K'=K/2 \end{aligned}$$

(35)

is strictly negative ($R<0$).

The condition on the negative sign for R is fulfilled only if $p'<0$, that is if $a>\sqrt{3}$. Therefore, in order to have $R<0$ and thus three real solutions, the anchor point a of the straight line must be located well outside the Lorentzian line shape. This first condition on a being assured, the factor R is negative for values of the reduced slope $K'$ lying within the two roots of the polynomial (35). The explicit values for these roots can be evaluated through the reduced discriminant:

$$\begin{aligned} \Delta '=b^2\left( b^2+1\right) -\frac{18b^2+1}{27}, \end{aligned}$$

(36)

which is a quantity unconditionally positive since $b>(1/3)$. The two roots $K'_{1,2}$ of (35) are finally: $K'_{1,2}=b\left( b^2+1\right) \pm \sqrt{\Delta '}$.

To summarize, for a given detuning $a>\sqrt{(}3)$, the bistability range of the system described by Eq. (33) corresponds to the zone where the reduced slope $K'$ lies between the two roots $K_{1,2}$ of (35), where $R<0$.

Fig. 9

Intersection of a straight line of variable slope K and anchor point a with a Lorentzian curve. The vertical blue dashed line correspond to the linear regime, whereas the two green-dashed lines delimit the range of bistability inside which two or three distinct real solutions may exist