Abstract
We have performed a series of feasibility tests toward deployment of quantum key distribution (QKD) systems in commercial optical fiber TELECOM network. By monitoring of the operation of selected state-of-the-art QKD systems with a typical commercial imperfect communication line in the role of quantum dark channel we have assessed stability and reliability of two quantum cryptography systems, on nonentangled and on entangled photons. The quantum bit error was the main observed parameter which allowed for quantitative assessment of both systems operation efficiency and their resistivity to random perturbations including hacker attacks in noisy environment. The comparison of both systems with respect to their tolerance against noise and technical imperfections of a dark quantum channel has been presented.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The progress in quantum cryptography is related with implementation of quantum key distribution (QKD) scheme for symmetric OTP (One Time Pad) cryptography system upon the BB84 (Bennett and Brassard 1984), Sarg04 (Scarani et al. 2004) and E91 (Ekert 1991) protocols. The latter protocol is addressed to entangled flying qubits (pair of quantumly entangled photons) whereas two former ones are referred to nonentangled quantum information carriers—ordinary single photons. Though the particular practical implementations of the entangled and nonentangled QKD schemes differ significantly, in both cases the quality of quantum dark channel determines constraints and limits for secure communication and discriminates both its range and speed. In the present paper we report the comparison of two commercial nonentangled and entangled QKD systems tested versus quality of the quantum dark channel with emphasizing of feasibility study toward potential deployment of QKD systems in commercial TELECOM optical fiber network infrastructure.
1.1 QKD nonentangled system
QKD cryptographic system called Clavis II, produced by Swiss company idQuantique, is a quantum device using nonentangled photons as mobile qubits. The quantum states of photons are here defined by phase shift measured in two mutually orthogonal bases, with phase shifts 0 and \(\pi\) in the first basis and \(\pi /2\) and \(3\pi /2\) in the second one. The phase differences of e-m impulses corresponding to single photons allow to establish quantum interference registration in Mach–Zehnder interferometer system—Fig. 1. Beam splitters indicated in the interferometer scheme (Fig. 1) are glass plates covered with thin (semi-translucent) silver layer. This layer reflects half of the beam while allowing the other half to pass through. According to the rules of e-m wave phase shift at reflection, the change of phase to the opposite occurs only at reflection from a plane behind which a more optically dense medium is present. Hence, reflection from the splitter causes phase shift only when photon falls on the silver layer from the side of the air. The photons are registered by the pair detectors depending on quantum random choice at the beam splitters. Together with the phase modulators the BB84 or SAR04 protocols can be implemented. Technical implementation of this system is shown in Fig. 2.
Technical implementation of Clavis II system [based on IdQuantique (2010)]
In the system Clavis II the 500 mW laser (semiconducting laser diode) generates short light impulses with a wavelength (1310 nm—infrared, adjusted to single-mode fiber characterized by high transmission rate in this wavelength range), which are directed along optical fiber to circulator. Waveguide circulator is a standard element of optical fiber technology—signal entering it is transmitted to the next port in clockwise rotation (circulation). Single photon detectors (based on avalanche diodes) are used to register photons in Mach–Zehnder interferometer. The detectors (avalanche diodes) are located only in the Bob part and are used to measurement by Bob and by Alice due to an appropriate redirecting of photons from Alice to Bob along with simultaneous changing their polarization in Faraday mirror. Faraday mirror is a simple mirror, in front of which there is situated an optically active element (controlled with a magnetic field) that changes the polarization of passing photons by \(\pi /4\). After being reflected, the photon again passes through this element and hence goes back with a reversed polarization (\(\pi /2\)). Conversion of the polarization of photons returning to Bob allows to use the same detectors at the Bob side. This ingenious solution has an additional advantage—the optical paths for both directions are ideally compatible and the distance between Bob and Alice does not introduce any phase shifts regardless of the connection length. . Such a solution is advantageous for extending the communication range, as attenuated returning impulse moves only one direction (form Alice to Bob), while in the opposite direction (from Bob to Alice) the beams power is greater (and hence more resistant to losses in the transmission line). Situating lasers and detectors only in the Bob part results in the Alice part containing only cheap and simple system elements, which is a significant advantage of the Clavis II system.
In the Alice station it has been applied a delay line (in the form of 24 000 m of fiber coil) in order to avoid mistakes during detection. It plays a major part in synchronizing of the system operation. A many kilometers long delay line is adjusted to contain a complete train of impulses in order to avoid the impulse conflict on the Alice phase modulator. The Alice station entry has also a filter that removes incidental photons resulting from e.g., Rayleigh scattering in the fiber.
1.2 QKD entangled-photon system
Designed and manufactured by AIT (Austrian Institute of Technology, Vienna Universitys spin-off) EPR S405 Quelle is the QKD system using entangled photons (Ekert 1991; Enzer et al. 2002; Pan et al. 2001; Ekert et al. 1992; Lindenthal 2006). The function of mobile qubit is played by photons quantum states encoded in their polarization. Entangled photon pairs are here created in the process called Parametric Down Conversion (Burnham and Weinberg 1970) in a birefringent crystal BBO (beta barium borate).
Generation of entangled photon pair in birefringent, nonlinear crystal BBO; as a result of photon decays into two photons with half energy each (nonlinear effect called Parametric Down Conversion), in the birefringent crystal there are created two conical photon beams with opposite polarization (upper beam with vertical polarization and lower beam with horizontal polarization); at the intersection of the cones, the states have not determined polarization and describe pairs of entangled photons
In the BBO crystal, photon with energy \(\hbar \omega\) decay upon nonlinear process into two photons, each with half the original energy \(\hbar \omega /2\). The crystal is also birefringent, which means that generated photons travel along various paths depending on the polarization. With the crystal appropriately configured, there are created two conical beams, the upper one with vertical polarization and the lower one with horizontal polarization—cf. Fig. 3. At the intersection of these two beams photons do not have a defined polarization—there is created an entangled state of two photons. In the Quelle system it is used BBO crystal illuminated by laser diode [with power 500 mW and wavelength 405 nm (violet)]. The laser beam is concentrated on the surface of about \(25\,\upmu \hbox {m}\) radius in an appropriately cut crystal 4 mm in length. Entangled photons have wavelength 810 nm (near infrared) and are separated by small prism mirrors. In the next step both beams are concentrated on half-wave plates by lenses with focal length 1.5 cm and then directed at additional small (0.5 mm thick) crystals BBO in order to compensate the delay of signals with different polarization (due to birefringence, the signals with different polarizations move in the crystal with different speeds).
The Quelle system admit to organize communication between Alice and Bob blocks over quantum fiber channel or, alternatively, with telescope open-air connection. According to the producer (AIT), the fiber connection has the range of about 50 km, while the telescopic connection has the range of approximately 1 km.
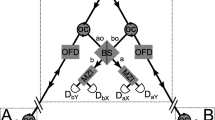
In EPR S405 Quelle system the Alice block is more complicated than the Bob one—the former one contains a component generating pairs of entangled photons. Although the Bob block is less complicated, both blocks contain rather expensive elements, i.e., complete sets of avalanche diode detectors (four in Alice station and four in Bob station) (Fig. 4).
A scheme of Quelle system with indicated design of detector blocks—entering photon falls into a randomly chosen polarization beam-splitter either directly, or indirectly, through half-wave plate, which is equivalent to random selection of ON basis for polarization measurement in each of the two, Alice’s and Bob’s, detector blocks [based on Austrian Institute of Technology (2010)]
The measure of quantum transmission quality is QBER (Quantum Bit Error) displaying the ratio of false and discarded qubits to the total number of qubits exchanged in due of the row key creation. To reduce its value there are used error correction procedures and privacy amplification procedures performed over the public connection. The sources of errors are technical imperfections of the system and a possible eavesdropping. In the case when the number of errors exceeds a preset error limit, the connection is considered to be eavesdropped and the whole key is discarded. In the case when the number of errors does not exceed the limit, correction procedures allow to eliminate errors efficiently (to any desired level), but at the cost of reducing the length of an original raw key. The eventual QBER of a single percent order is considered as good enough to use the secret key in public channel communication between Alice and Bob.
The Clavis II system is a commercially available product, whereas the Quelle system is rather laboratory equipment. Sophisticated sensor system, especially temperature sensors for Clavis II is also a mark of technological advancement and the designs refinement. What deserves criticism in Clavis II, is the usage of non-standard optical fiber terminals and connectors, which necessitates modifications when fibers are changed. Another disadvantage of Clavis II system is its sensitivity to temperature—as was experimentally tested in NLQT WUT, the system stops working at temperature above 27 °C, which means that additional cooling must be provided in the server room, where Clavis II stations are located, especially in moderate or hotter climate conditions.
EPR S405 Quelle is a far more complicated optoelectronic system, as compared to Clavis II. It is also less refined and reliable—its operation requires more precision and is less automated. On the other hand, the Quelle system uses entangled photons and therefore it may be judged a more sophisticated quantum device than systems using non entangled photons. Using entangled states makes it possible to exclude some forms of attack on quantum channel and this is considered to be the system advantage.
2 Stability assessment of QKD procedures in commercial quantum cryptography systems versus quality of dark channel
The quantum cryptography protocols as e.g., BB84 (Bennett and Brassard 1984), E91 (Ekert 1991), SARG04 (Scarani et al. 2004), are designed to execute a safe and repeatable exchange of the secret cipher between two distant communication parties (Alice and Bob). This continuously renewing cypher can be next used for encryption and decryption of arbitrary classical messages exchanged between these parties over ordinary public channels upon the OTP cryptographic scheme. Though the absolute security of the QKD protocol is proved in theory (Nielsen and Chuang 2000; Bouwmeester et al. 2000; Lo and Chau 1999; Ferenczi et al. 2012) the practical its implementations suffer from technical imperfections (Scarani et al. 2009). To reduce inconvenient and generally unavoidable technical imperfections as much as possible is of primary importance to guarantee the highest security level and to enhance the range of communication. To optimize operation mode and to calibrate all elements of the QKD hardware, including photon sources, phase modulators, detectors, connectors etc., are of crucial importance for successful detection and rejecting of potential hacking attacks, which usually are designed to be covered with noise (Lydersen et al. 2010). Inconveniently, the present QKD systems undergo the fast and frequent self-decalibrations in due of operation, which perturbs the smooth and stable repeating of cypher creation cycles and causes the frequent restart of the calibration procedure. The eventual solution of this problem might be an automatic restoring of the system calibration controlled by appropriately designed sensors monitoring quality of QKD setup operation.
We have performed an observation of the work-parameters of the selected state-of-the-art QKD systems (the non-entangled photon based Clavis II by id-Quantique and the entangled photon based EPR S405 Quelle by Austrian Institute of Technology). The observed parameters are (Zbinden et al. 1998; Gisin et al. 2002): the raw key exchange rate (RKER), and the quantum bit error rate (QBER). Both these complementary parameters supply information on operation quality of the system. RKER displays the efficiency of secrete key creation, whereas QBER counts errors in this process. The larger RKER and lower QBER the better status of cypher creation is. Worsening of RKER and QBER is due to sum of all technical imperfections of the systems and also due to possible eavesdropping by a third party (Eve). An eavesdropping causes usually rapid enhancement of QBER and dropping of RKER. Therefore to keep all sources of noise as low as possible is crucial for monitoring of potential eavesdropping attacks. Of a particular significance is the quality of the dark quantum channel because this element of the whole system is most vulnerable to any unpredictable perturbations resulting in large noise and decalibration of the systems. It must be emphasized that Qelle and Clavis II utilize distinct photon properties as flying qubits. In the system Clavis II the phase of electro-magnetic wave is selected by quantum random number generator and attributed as the flying qubit. As the phase shift depends on optical wave, thus the length of optical fibers might shift the phase in an uncontrolled manner. This problem is solved in the Clavis II setup by usage of the same fiber to send qubits from Alice to Bob and vice versa, dismissing in this way the importance of the dark channel length. The remaining limitation due to the dark channel length is an overall attenuation level of the used optical fiber. To avoid interference between qubits flying forward and back through the same fiber in the same time, it is applied the Faraday mirror at the end in the Bob setup, which change orthogonally the polarization of reflected photon with respect to incident one, preventing in this way their mutual interference.
In the case of the Quelle system photon pairs are entangled in their polarization, thus the polarization of photons is attributed to qubits. Polarization of photons might be, however, easy changed in due of traversing the optical fiber. Any polarizing elements of the dark channel (optical fiber with connectors) may randomly measure polarization of carriers modifying or destroying in this way carrier entanglement. Even though it is well known that the Schmidt number (Nielsen and Chuang 2000) of the entangled pair of qubits cannot be reduced neither by qubit space-separation nor by single-qubit measurement (Nielsen and Chuang 2000), but the Alice and Bob registering of polarization on their own detectors take place in distinct time moments and any miss-mash of polarization violates the measurement correlation. Moreover, the scenario of the teleportation (Nielsen and Chuang 2000) demonstrates that by two-qubit measurement of a one part of originally entangled pair with a third qubit leads to a disentanglement of the original pair, which also may violate the dark channel communication and increase QBER. Hence, an avoidance of polarizing elements in the dark channel fiber of the Quelle system is of higher importance in comparison to the Clavis II system. In the latter case the polarization shift along the fiber do not influence qubit states, though may change the photon polarization preventing interference of incident and reflected photons.
For the testing of the dark channel influence onto the quality of quantum communication between Alice and Bob and on the system decalibration rate we have controlled perturbation of this channel via including varied number of 2 m long fragments of the optical fiber into the transmission line with standard (FC/PC) connectors. We suspected that the quality of the quantum communication channel is determined mainly by the number of the connectors or weldings (typical in commercial optical fiber infrastructure) and actually they are the strong source of the signal decoherence due to their polarization and attenuation effects.
Because connectors and weldings are frequently used in metropolitan fiber networks, hence the examination of their influence onto QKD procedures is valuable in view of possible practical deployment of quantum cryptography in commercial TELECOM webs.
Comparison of Raw Key Exchange Rate (left) and Quantum Bit Error Rate (right) for the non-entanglement based QKD system with the dark channel with one (upper) and five (lower) FC/PC connectors along the transmission dark line; the strong override of fluctuations by heavy noise caused by connectors is noticeably in the lower charts
The measurements of the RKER and QBER in series of the QKD sequences with different number of the 2 m long fiber patchcords connected together into the dark transmission line allow for assessment of the quality of the dark channel influence onto efficiency of QKD. The RKER and the QBER serve as the quality-assessment-parameters for the QKD process. The charts (Fig. 5) present: the X-chart (the plot of measured values with dependence on the number of the QKD sequences), the histogram of the measured values, the plot of the data deviation from the normal distribution (for typical stable process, data of the control parameter are expected to satisfy the normal distribution), the results of the configuration tests (the tests of the randomness of the control parameter).
The red line in Fig. 5 is the control line (CL) corresponding to the average value of the controlled parameter, while usually called LCL and UCL lines limit a region of a width of six standard deviations centered at the average value (as indicated in Fig. 6 and next in Fig. 9). The points beyond the LCL and UCL indicate a dysregulation of the system and are marked with a different color (red in Fig. 6 and next in Fig. 9).
The influence of the number of the patchcords with connectors onto the operation parameters (RKER and QBER) was examined via the comparison of the average RKER and QBER values obtained with different numbers of the connectors included along the transmission line (as visualized in Fig. 7). Even though the change in the number of the connectors in the dark line does not affect the Bob and Alice stations, the collected data are expected to be useful to carry out the statistical cluster analysis and to verify trends in the data in control charts (as summarized in Fig. 6).
The particular number of the connectors along the transmission line was varied between one and seven. For each number of connectors, the data have been gathered during the continuous work of the system (the repeating of the quantumly generation of the secret keys) within a periods of 20–50 h for Clavis II resulting in the generation of few hundreds of keys with 512 bits each. For our analysis, a single probe is identified in this case with a single key generation. For the Quelle system, the time of the continuous work has been restricted to about 1 h because the system is not fully automated and requires the repeating manual calibration after that period. For the Quelle system, the single probe is assumed to correspond to a single bit of the key to increase the density of probes per the measurement period.
The statistical analysis of the gathered data for RKER and QBER for the non-entanglement based QKD system with dark channel with one connector (upper) and with five connectors (lower): the histograms of RKER (left), the corresponding X-charts for RKER (middle), the X-charts for QBER and QBER normal probability plot (right); small deviation from normal distribution is noticeable for larger number of connectors. In histograms the decalibration points are indicated in orange, their number sharply grows with number of connectors
2.1 Test of QKD system with non-entangled photons
The study has been performed with the commercial Clavis II system of the plug-and-play architecture that utilizes the coding of the quantum information in the phase to the electro-magnetic wave selected by the quantum generator of random numbers. As mentioned above the Clavis II system utilizes the same optical path to transmit the photons back from Bob to Alice when they were sent originally from Alice to Bob. In this manner it is possible to employ only one pair of single-photon detectors only on the Alice side. This results in considerable simplification of the optical arrangement in comparison to the polarization-coding system Quelle (Muller et al. 1997; Zbinden et al. 1997) where the doubling of detectors is required. The system Clavis II offers optionally the QKD SARG04 or BB84 protocol implementations. For presented tests we have chosen the BB84 protocol because it is the most popular, thus, convenient for comparison analysis.
Via the comparison of the scatter graphs for the RKER and QBER [Fig. 5, for two situations: the dark channel with single connector (upper charts) and the dark channel with five connectors (lower charts)] we cut a single time window from each series of the measurements that corresponds to the most stable work. The selected data have been next used for the statistical analysis. The corresponding area of the data are indicated by points ranged with the blue contour in Fig. 5. The X-charts and corresponding histograms are presented in Fig. 6 for the RKER and QBER, which have been prepared with the selected series of data (from Fig. 5). In the X-charts in Fig. 6 the deregulation points are indicated with the red color. They appeared to be rather numerous despite quite constant external conditions for the system operation. The histogram for the RKER (Fig. 6) deviates from the normal distribution histograms with increasing number of connectors indicating a systematic error source. In Fig. 6, the small deviation of the QBER from the normal distribution is also visible (growing with the number of connectors). This motivates us to apply the cluster analysis (comparative distribution tests) for the pairs of the different series of data. We utilize the Mann-Whitney U-test, ANOVA (Kruskal-Wallis), and median test. None of these tests has confirmed the existence of correlations between different data series. Therefore, we conclude that there is not any universal QBER distribution pattern, which assures us that the deregulations of the system seen from the X-charts occur at random measurement points and are not connected to a systematic outcome bit distribution of any particular element of the system but are rather manifestation of a systematic defect of the whole complex system.
The comparison of QBER and RKER for the Clavis2 system with the original 6.5 km long dark channel prolonged with consecutive 1–72 m long fiber pieces connected together into the final dark channel indicates clearly the central role of the quality of the dark channel for efficiency and fidelity of the system operation. Both parameters, QBER and RKER reveal worsening of QKD operation with increase of connector number. As it is visible from comparison of charts in Figs. 5 and 7, the lowering of RKER and increase of QBER is relatively large (allowing for monitoring of this increase/decrease by adding connectors) and at the number of 5 connectors, other imperfections of the system are overridden by the error source caused by the connectors. At the level of increased QBER and reduced RKER due to numerous (5) connectors in dark channel all other fluctuations are relatively reduced. This reveals the quickly growing weakness of the dark channel with increase number of connectors, diminishing in this way the security level of the whole implemented cryptography system. Simply, a small noise signal caused by possible eavesdropping attempts could be covered by larger noise caused by connectors. Despite worsening operation parameters the Clavis2 still creates the secret cipher but the possibility to notice potential eavesdropping by some additional fluctuations of QBER or RKER diminishes. This reduces immunity of QKD in such a case and emphasizes the role of the quality of the dark channel. For high lever secure quantum connections the smooth continuous fibers should be thus applied and utilization of standard connectors, typical in commercial fiber communication networks, must be severely limited.
2.2 Verification of the Quelle system deployment in commercial metropolitan fiber network
The Quelle system has been designed to implement E91 protocol (Ekert 1991) accommodated to entangled flying qubits. In the Quelle system, flying qubits are associated with the polarization of photons because entangled pairs are created by the Parametric Down-Conversion (Burnham and Weinberg 1970) in a birefringent nonlinear crystal beta Barium Borate (BBO).
For generating photon pairs in the Quelle system it is used 405 nm laser beam which generates pairs of photons of 810 nm wave-length. In principle this wave-length could be shifted by usage of another wave-length laser (or even a tunable laser) as the Parametric Down-Conversion properties of BBO crystal are maintained in larger range of frequencies. An application of another laser would result in distinct wave-length better accommodated to optimal Alice-Bob transmission requirements. 810 nm wave-length fits to the so-called first telecommunication window, which was suitable to transmit light within 800–900 nm band. The problem with such a window is that fibers have relatively high losses at these wave-lengths. The development of fiber networks led to utilization of the so-called second telecommunication window. This window is defined around 1300 nm wavelength. Current optical networks employ mostly the next convenient window at ca. 1550 nm for optimal wave-length (called as third telecommunication window) because of better transmission properties of optical signal with this wave-length even over relatively long distances.
Despite the large incommensurability between photon wave-length and optimal transmission window in the present standard TELECOM networks it is interesting to verify efficiency of quantum communication over such lines. In the case of insufficient effectiveness of system work in such incommensurability condition one would take into account that the better matching of wave-length can be achieved by changing either the laser in the system or the network fiber. The latter solution is, however, especially inconvenient as connected with high cost for new large scale dark channel installation and exchange of the laser seems to be a better solution.
We summarize here the series of tests which have been carried out on the Quelle system using various configurations of standard 1550 nm wave-length optical fibers for quantum dark channel between Alice and Bob stations of the system. The parameters of the system functioning were monitored and registered using the appropriately designed data card and compared to the optimal functioning of the system at laboratory conditions. The QBER is observed in time when the secret key is created and distributed between Alice and Bob over the quantum channel. The series of data collected by use of the monitoring card allows for assessment of quality of the quantum communication over the fiber connection especially in view of coherence losses due to polarization perturbations. This is a central problem, even more important than the signal attenuation caused by discrepancy of the optimal transmission window of the fiber with photon wave-length, because polarization is the information carrier (flying qubit) in the considered system.
The quantum state of photons in the Quelle system is the entangled state with respect to their polarizations. In the mixed state of single photon of the entangled pair none polarization is determined, i.e., this is a mixture of both mutually orthogonal polarizations according to general rules of the entanglement (Nielsen and Chuang 2000). The photon source is located in Alice block, but it may be installed as a separate element of the system somewhere in between Alice and Bob. The entangled photons are delivered to Alice and Bob detectors, in which their polarizations are measured in randomly selected orthogonal (ON) bases (of two possible bases–vertical-horizontal \(0,\;\pi\) and diagonal \(\pi /4,\; 3\pi /4\)). In the next step Alice and Bob use the public channel to determine only those of the measurements in which the same bases were selected by both parties, but not revealing the particular measurement results. That way a shared secret key of classical bits (results of measurements) is generated in a raw form, which undergoes next a classical treatment (error correction and privacy amplification), identical to all cryptographic key generation procedures, including QKD. The first part of E91 protocol, although different in photon entanglement from standard BB84 procedure (Bennett and Brassard 1984), is in fact equivalent to the latter. It is, however, believed that using entangled states positively influences security level, but it has not yet been rigorously proved with all details. Nevertheless, analysis of attack detections in case of entangled carriers indicates better performance of such systems. Ekert (1991) suggested that his protocol security level could be increased by using Bell inequality (Bell 1964), which is connected to quantum entanglement and direct application of this criterion for detecting a possible eavesdropper (unfortunately, the suggested procedure requires using a third basis for measurement and developing the system with more detectors) (Curty et al. 2004; Garg and Mermin 1987). This approach also allows, on the other hand, to directly verify entanglement of the states of photons emitted by the source.
In the case when the number of errors does not exceed the predefined limit, correction procedures allow to eliminate residual errors efficiently (to any desired level), but at the cost of reducing the length of original raw key. The QBER achieving a fraction of percent up to single percent is considered as a result good enough to use the generated key in open communication between Alice and Bob.
In the case of photon pair produced and employed to communication in the Quelle system, the mutual correlation of polarization of both counterparts of the entangled pair is fixed after the measurement by Alice, which encoded a bit of cypher into it. The correlation between photons can be, however, perturb during the transmission of the photon to Bob in a fiber. The unavoidable drift of polarization in the fiber due to its bending, strain induced birefringence, defects in connectors and in welding regions results in the redefinition of the correlated carrier polarization. Photons are still correlated, but we do not know the value of an unpredictable polarization drift. As the measurement at Bob station takes place after some time delay with respect to the Alice measurement, the mentioned polarization drift can violate the measurement correlation. To restore the required measurement correlation the manual polarization controller is applied. By the manual tuning of polarization controller manipulators (changing polarization of photons in the twisted fiber) one can achieve minimization of the number of counts on each path (on detectors which are counting photons with polarization perpendicular to the selected one by polarizers). This method allows for restoring of the initial correlation. This correlation is of quantum character and the tuning improves its manifestation in due of QKD procedure. This circumstance reveals a sever imperfection of the system Quelle operating with optical fiber dark channel. The random drift of polarization along twisted fibers with strain at weldings and connectors, even if instantly compensated, produce generally errors, hard to completely avoid.
Nevertheless, if instead of the optical fibers one uses the open air dark channel (according to the producer (Austrian Institute of Technology 2010), open-air dark channel is efficient over the distance of 1 km) the fidelity of entangled state conservation grows. In the atmosphere the decoherence is, however, large due to e.g., a fog or a dust and gaseous particles interacting with photons. This severely limits the coherence distance and only out of the atmosphere, in a cosmic space, the condition for entangled polarization QKD system might be considerably improved.
The manual tuning procedure is not ideal and is monitored by the restored correlation rate (the ratio of properly correlated pairs to the total number of pairs), the so-called visibility ratio. This ratio, when is higher than 0.9, is assumed as good enough to start communication over the quantum channel.
For the test of the Quelle system for the reference ideal quantum channel we used two 1 m long 810 nm patch-cords connecting both parties (Alice and Bob subsystems). Stable room temperature was maintained (around 20 \(^\circ\)C). When short patch-cord connection is used, photon count numbers at both communication sides are at similar level (130,000 to 150,000 counts per single cycle of cypher generation limited by de-correlation of the photon pair polarization). In this case, we assume that the system works in an optimal manner without information losses in the quantum channel. Errors are caused only by other imperfections of the system out of the dark channel. After restoring polarization correlation as was described above, the system was restarted and the next cypher exchange has been continuously performed in duration of around 15 minutes. Then, the system was stopped, the log-file was copied and used as an input file for GNU R script responsible for the extracting, formatting and plotting data.
(upper left) QBER for entanglement based QKD system with 810 nm fiber for dark channel measured during time window in seconds; (upper right) 3 runs of entanglement based QKD system (over 600 m long 1550 nm fiber)—rapid increase of QBER indicates improperly functioning of the system; (lower left) 2 runs with different fiber length (orange—200 m; blue—400 m) with 1 h time window (higher ratio of polarization drift on shorter fiber probably due to lower quality of FC/PC connector); (lower right) 3 runs with different fiber length (orange—200 m; blue—400 m; purple—800 m) with 1 h time window. (Color figure online)
As we see from Fig. 8 upper left, the corresponding process of generation of secret key using the quantum channel with wave-length 810 nm reference short fibers in 15 minutes time window is stable, which we assume as the standard-mode of system operation.
For testing of commercial fibers with telecommunication window (1550 nm), we have used SMF-28 fiber with the following parameters: core diameter \((\upmu \hbox {m})\): 8.2; cladding diameter \((\upmu \hbox {m})\): 125 ± 0.7; coating diameter \((\upmu \hbox {m})\): 242 ± 5; maximum attenuation for 1310 nm (dB/km): 0.33 to 0.35; maximum attenuation for 1550 nm (dB/km): 0.19 to 0.20; maximum attenuation for 1625 nm (dB/km): 0.20 to 0.23; dispersion for 1310 nm (ps/nm km): less than 1.0; dispersion for 1550 nm (ps/nm km): less than 18.0; dispersion for 1625 nm (ps/nm km): less than 22.0; temperature dependence (C): \(-60\) to \(+85\); single fiber length (m) in patch-cord: 802 ± 10; number of weldings/connectors in patch-cord of 6.5 km for length: 5–7.
After restoring the proper polarization correlation before each measurement (in the same manner as described above) and achieving an acceptable QBER level, we started recording the measurement of QBER value over iterating series of QKD process repetitions. The collected results are summarized and plotted in Fig. 8 upper right, where three distinct runs of the system with 600 m length dark channel are illustrated. In Fig. 8 lower left and 8 lower right, the QBER observation for dark channel 1550 nm fiber with length 200, 400 and 800 m, for comparison are plotted.
Control charts generated for above measurements show clearly that there are strong external or internal decoherent/destructive factors that are affecting the whole process. The initial QBER is quickly and continuously rising during the process. Moreover, after obtaining QBER value higher than 10 percent, the system stops because of too high value of error ratio. Twice repeating the measurement this threshold value was obtained very quickly (after 454 and 438 seconds, correspondingly).
The outcome of the above described test can be summarized as follows. Current implementation of entangled photon QKD system, Quelle, suffers from the lack of efficient automatic polarization stability control instantly preventing depolarization. By polarization stability, we mean ability to properly pre-defined entangled pairs with perpendicular a’posteriori polarizations in both communicated parties, i.e., with required polarization correlation in the entangled pair after the measurement. Without this ability, the data transmitted through the quantum channel are randomly identifying with constantly rising number of errors, which interrupts quickly the connection. To restore communication, the thorough and time-consuming manual regulation of polarization is necessary, which makes all the communication practically impossible.
To overcome this highly inconvenient tendency we propose to replace the manual polarization control with an efficient automatic one. Automatic polarization controller would instantly compensate polarization drift and recover the system functionality. Such an improvement of the Quelle system would result in maintaining a sufficiently low and stable value of QBER ratio allowing entangled QKD over even commercial network, though still for distance not longer than ca. 1 km and without weldings and connectors. The performed tests indicated also that in order to improve quality of 1550 nm quantum channel, the shift of wave-length of photons is necessary by application of lower energy laser activating BBO crystal. This would allow for better matching of optimal window for transmission of the standard 1550 nm fiber. As it follows from the test, the welding decreases quality of quantum channel in a critical manner, which is probably connected with additional polarization mishmash due to a strain and imperfections in the region of welding or of standard connections. The worsening influence of connectors in the dark channel on the Quelle system operation is visualized in Fig. 9. Thus, for establishing of efficient quantum channel avoiding of weldings and connectors is necessary.
3 Conclusion
The main obstacle for practical utilization of quantum cryptography systems are technical implementation imperfections. The theoretically ideal, arbitrary long dark quantum channel is severely reduced by unavoidable decoherence of flying qubits. We have tested several typical commercial communication patch-cords of optical fibers supplied by the TELECOM company, which were the same as installed in metropolitan network. The tested fibers were interrupted with numerous weldings and standard fiber connectors also typical in telecommunication practice. The commonly used fibers commercially operate at transmission window close to 1550 nm (infra-red) and the usefulness of such fibers to apply as quantum channel was verified experimentally.
A series of tests on Clavis II and Quelle systems was performed at conditions of the real commercial fiber network, which allowed to estimate the possibility of using the systems within existing commercial optical fiber infrastructure. The tests included also model quantum connections with the quality reduced by multiple optical fiber weldings and connectors. The results can be summarized that the possibility of using both QKD systems in existing telecommunication networks is strongly limited by insufficient quality of standard commercial optical fiber lines.
Summarizing these QKD system examination we can state that the worsening of the dark channel for QKD protocol implementations by adding short (2 m long) pieces of the optic fiber connected to the whole line with standard connectors (FC/PC) directly demonstrates the crucial role of the quality of dark channel for quantum communication and efficiency of the system operation. The system Clavis II utilizing as the flying qubit the phase of light randomly selected by a quantum number generator still creates the secret cypher shared between Alice and Bob, but the security level of the procedure quickly goes down with increase of connector numbers. At the presence of more than 5 connectors the noise is overwhelmed by phase errors caused by connectors which override other fluctuations including possible QBER and RKER perturbations caused by potential eavesdropping attacks. Thus despite the seeming stability of the system the too high level of errors dismisses security of the QKD system. To maintain the high immunity of the system against hacker attacks taking advantage from system technical imperfections the maximal reduction of typical network connectors must be thus kept, and the continuous fiber for the dark line without any inter-connectors is recommended.
The self-deregulation of the operating commercial QKD systems has been shown to be permanent inconvenient and unavoidable property of the setups under examination, both for entangled and nonentangled QKD implementations. The systems spontaneously undergo a continuous decalibration drift which needs cyclic jump-wise compensation. After an initial calibration, the Clavis2 system works stably within a tens of sequences of the key generation only, while the Quelle system is stable during a few sequences at most. In the consequence, the monitoring of possible hacking attempts may be inefficient in practice. Additionally, unlike the Clavis II system, the Quelle system is not fully automated and its work requires tedious manual compensation of the polarization drift at the beginning of the each QKD session. This complicates the observation of the changes of the average QBER with the variation of the number of connector along the quantum transmission line, because these changes interfere with the spontaneous decalibration of the system. We suppose that this decalibration is caused by the method of the synchronization of the system elements. The software of the QKD systems can be responsible for the problem. With this regard, the standard measures used to assessment of the quality of the QKD transmission like the average RKER and QBER turn out to be not especially sensitive indicators of the security and operation-quality of the entangled QKD implementation whereas the time-period of the stable operation seems to characterize better the cryptography transmission quality and the security level. To improve the operation status of the Quelle system on entangled photons, being especially vulnerable against noise and decalibration, application of an automatic calibration system would be of order.
References
Austrian Institute of Technology: AIT QKD Software Project Documentation. AIT, Wienna (2010)
Bell, J.S.: On the Einstein–Podolsky–Rosen paradox. Physics 1, 195–200 (1964)
Bennett, C.H., Brassard, G.: Quantum cryptography: Public key distribution and coin tossing. In: Proceedings of IEEE international conference on computers systems and signal processing (Bangalore, India), pp. 175–179 (1984)
Bouwmeester, D., Ekert, A., Zeilinger, A.: The Physics of Quantum Information. Springer, Berlin (2000)
Burnham, D.C., Weinberg, D.L.: Observation of simultaneity in parametric production of optical photon pairs. Phy. Rev. Lett. 25, 84–87 (1970)
Curty, M., Lewenstein, M., Lutkenhaus, N.: Entanglement as a Precondition for secure quantum key distribution. Phys. Rev. Lett. 92, 217903-1–217903-4 (2004)
Ekert, A.: Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991)
Ekert, A.K., Rarity, J.G., Tapster, P.R., Palma, G.Massimo: Practical quantum cryptography based on two-photon interferometry. Phys. Rev. Lett. 69, 1293–1295 (1992)
Enzer, D., Hadley, P., Gughes, R., Peterson, C., Kwiat, P.: Entangled-photon six-state quantum cryptography. New J. Phys. 4, 45.1–45.8 (2002)
Ferenczi, A., Narasimhachar, V., Lütkenhaus, N.: Security proof of the unbalanced phase-encoded Bennett-Brassard 1984 protocol. Phys. Rev. A 86(4), 042327 (2012). doi:10.1103/PhysRevA.86.042327
Garg, A., Mermin, N.D.: Detector inefficiencies in the Einstein–Podolsky–Rosen experiment. Phys. Rev. D 35, 3831–3835 (1987)
Gisin, N., Ribordy, G., Tittel, W., Zbinden, H.: Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002)
IdQuantique: Quantum Key Distribution System id 3100 Clavis2 User Guide (IdQuantiqe, Geneva) (2010)
Lindenthal, M.: Long-distance free-space quantum communication with entangled photons. Ph.D. thesis, Vienna University, Vienna (2006)
Lo, H.-K., Chau, H.F.: Unconditional security of quantum key distribution over arbitrarily long distances. Science 283, 2050–2056 (1999)
Lydersen, L., Wiechers, C., Wittmann, C., Elser, D., Skaar, J., Makarov, V.: Hacking commercial quantum cryptography systems by tailored bright illumination. Nat. Photon. 4, 686–689 (2010)
Muller, A., Herzog, T., Huttner, B., Tittel, W., Zbinden, H., Gisin, N.: “Plug and play” systems for quantum cryptography. Appl. Phys. Lett. 70, 793–795 (1997)
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)
Pan, J.-W., Simon, C., Brukner, C., Zeilinger, A.: Entanglement purification for quantum communication. Nature 410, 1067–1070 (2001)
Scarani, V., Acín, A., Ribordy, G., Gisin, N.: Quantum cryptography protocols robust against photon number splitting attacks for weak laser pulse implementations. Phys. Rev. Lett. 92(5), 057901 (2004). doi:10.1103/PhysRevLett.92.057901
Scarani, V., Pasquinucci, H.B., Cerf, N.J., Dušek, M., Lütkenhaus, N., Peev, M.: The security of practical quantum key distribution. Rev. Mod. Phys. 81, 1301–1350 (2009)
Zbinden, H., Gautier, J.D., Gisin, N., Huttner, B., Muller, A., Tittel, W.: Interferometry with Faraday mirrors for quantum cryptography. Electron. Lett. 33, 586–588 (1997)
Zbinden, H., Bechmann-Pasquinucci, H., Gisin, N., Ribordy, G.: Quantum cryptography. Appl. Phys. B 67, 743–748 (1998)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Jacak, M., Melniczuk, D., Jacak, J. et al. Quantum key distribution security constraints caused by controlled quality of dark channel for non-entangled and entangled photon quantum cryptography setups. Opt Quant Electron 48, 363 (2016). https://doi.org/10.1007/s11082-016-0624-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-016-0624-9