1 Introduction

A large proportion of the economy’s demand can be covered by recycling to alleviate pressure on ecosystems and to provide sustainability. Focussing on the economic benefits that recycling offers, the report by the European Environment Agency (2011) explains the role of recycling in the green economy and examines the evidence of the contribution of recycling in Europe. The interaction between job creation and recycling is also represented in the same report pointing out that “recycling generates more jobs at higher income levels than other forms of waste management”. It was also emphasized that while the recycling economy grows and develops it currently covers only a small proportion of European Union demand for many material resources.

The use of disassembly parts removed from the end-of-life (EOL) products is gaining enormous importance in that sense. Especially in the waste management of electrical-electronic devices which can harm soil and water resources, products need to be disassembled to remove parts assembled on it. In parallel to these advancements, disassembly lines are getting even more attention from both academia and industry. Such lines need to be constructed and managed in an efficient way to meet the demand for disassembled parts and have a flexible system. The disassembly line balancing problem (DLBP) is the problem of allocating disassembly tasks to workstations in such a way that one or more performance criterion is optimized. In a DLBP, several performance criteria might be considered for optimization; including the number of workstations utilised, cycle time and smoothness index (to have a smoother workload distribution among the workstations). As opposed to the assembly line balancing problem (ALBP), the DLBP may have several other objectives such as removing hazardous (requiring special handling) and mostly demanded parts at earlier stations. The precedence relations in DLBP are much complex as it includes AND precedence, OR precedence and complex AND/OR precedence relationships (Güngör and Gupta 2002). All AND predecessors of a task must be complete to initialize that task. However, completing at least one of the OR predecessors of a task is enough to initialize that task. The AND/OR precedence relationships contain both AND and OR precedence relations in the precedence diagram of the problem.

The pioneering works on the DLBP belong to Güngör and Gupta (1999, 2001). The problem has been shown to be NP-hard by McGovern and Gupta (2007a, b). A shortest-path formulation was proposed by Gungor and Gupta (2001) to solve the DLBP with task failures. Some exact methods have been proposed mainly based on a mixed integer linear programming (MILP) model utilizing CPLEX solver (Ren et al. 2018a). For example, Bentaha et al. (2015) proposed an exact solution approach for solving the DLBPs under uncertainty of task times, which are assumed to be random variables with known normal probability distributions. Mete et al. (2016a) developed a mathematical model for solving the DLBP considering resource constraints. However, such methods fell short in solving large-scale problems. Another drawback is the huge computational times to find the optimal solution and prove its optimality. For these reasons, heuristics and metaheuristics have also been developed to solve the variants of DLBP efficiently. Among others, McGovern and Gupta (2003) and Ren et al. (2018a) used 2-opt heuristic for multi-objective DLBP and multi-criteria decision making. Mete et al. (2016b) proposed a solution approach based on beam search algorithm for the DLBP.

Due to the NP-hard structure of the studied problem, many meta-heuristics have also been utilised to obtain timely manner near optimal solutions usually for the multi-objective DLBPs. A genetic algorithm based approach was developed by McGovern and Gupta (2007) for the multi-objective DLBP and hybridised with a neighbourhood search method by Kalayci et al. (2016) to deal with the sequence-dependent task times in DLBP. Kalayci and Gupta (2014) also used tabu search for the sequence-dependent DLBP. A variable neighbourhood search method was developed by Ren et al. (2018b) for the multi-objective DLBP. Swarm based algorithms, including ant colony optimization (McGovern and Gupta 2006; Agrawal and Tiwari 2008; Ding et al. 2010; Kalayci and Gupta 2013a), artificial bee colony algorithm (Kalayci and Gupta 2013b; Kalayci et al. 2015; Liu and Wang 2017), particle swarm optimization algorithm (Kalayci and Gupta 2013c; Xiao et al. 2017) and evolutionary algorithms (Ren et al. 2017; Zhang et al. 2017; Liu et al. 2018; Zhu et al. 2018) have also been developed for the variants of the DLBP. A recent survey by Özceylan et al. (2018) provides a comprehensive review of the algorithms applied to DLBPs.

Among the exact methods developed, the MILP model proposed by Altekin et al. (2008) aims at maximizing the profit while determining the parts whose demand is to be fulfilled to generate revenue. Koc et al. (2009) proposed two exact formulations that utilise an AND/OR Graph as the main input for the purpose of maintaining the feasibility. Altekin and Akkan (2012) developed a two-stage approach to rebalance the disassembly lines in the case of task-failure. Fuzzy goals were taken into account by Paksoy et al. (2013). A mathematical model and an ant colony approach were developed by Mete et al. (2018) to balance a hybrid line consisting of both assembly and disassembly tasks. Li et al. (2019a) proposed a branch, bound and remember algorithm for the simple DLBP. Li et al. (2019b) also developed a fast branch, bound and remember algorithm which is capable of achieving state-of-the-art results for simple DLBPs within 0.1 s on average. Wang et al. (2019) addressed to the stochastic two-sided partial disassembly line balancing problem and proposed a multi-objective discrete flower pollination algorithm.

Two basic outcomes are resulting from the literature review presented above. Firstly, multi-manned stations have been extensively studied for the ALBPs [see, for example Fattahi et al. (2011), Roshani and Giglio (2017), Kellegöz (2017) and Giglio et al. (2017) among others]. However, to the best of the authors’ knowledge, only one research has addressed to the DLBP with multi-manned workstations. Cevikcan et al. (2019) proposed a MILP model and two framework heuristics to minimize the number of operators and workstations. Nevertheless, multi-manned stations are handy in real applications to separate items given that the operators do not obstruct each other. The second basic outcome is that there is no research addressing the Type-E objective in the DLBP (denoted with DLBP-E), in which both cycle time and number of workstations are optimized concurrently (Kucukkoc and Zhang 2015). Moving from that point, this research contributes to literature introducing the Type-E DLBP with multi-manned workstations. While the main objective is to maximize the line efficiency, second and third objectives are also sought considering the hazardous and highly demanded parts to be removed first. A mixed-integer nonlinear programming model (MINLP) is proposed for the solution of small and some medium scale problems. Due to the complexity of the studied problem, a linear model, called iterative MILP model (iMILP shortly), is also developed for the large-scale problems and its solution building mechanism is demonstrated through a numerical example. Computational studies are conducted to measure the effect of using Type-E model on the line efficiency in comparison to the Type-I model (where the number of workstations is minimized given the cycle time). Furthermore, it was also investigated how enabling the utilization of multi-manned workstations helps increase the efficiency of the lines.

The remainder of this paper is organised as follows. Section 2 defines the DLBP-E with multi-manned workstations and presents the MINLP model developed for solving it. A numerical example is also provided in the same section with its optimal solutions depicted comparatively. Section 3 describes the proposed iMILP model for solving the introduced problem when the problem size is large. Computational tests are conducted in Sect. 4 and the conclusions are drawn in Sect. 5.

2 Problem definition

The DLBP consists of assigning a number of disassembly tasks (\(i \in I\)) to workstations (\(j \in J\)) with the aim of optimizing an objective function considering certain constraints, namely precedence relationship and capacity constraints. Commonly sought objectives in the literature are minimization of the cycle time (CT), minimization of the number of workstations (NS), removing the hazardous parts and parts with higher demand at earlier workstations. Some researches in the literature proposed linear hierarchical models only to minimize the number of workstations as a primary objective and considered removing the hazardous parts and parts with higher demand at earlier workstations as a secondary objective.

The term ti denotes the processing time of disassembly task for part i. Line efficiency (LE) of a disassembly line system is calculated dividing the total work content (the sum of processing times of parts to be disassembled, abbreviated as T) to the time period allowed to complete all tasks, \(LE = T/\left( {NS \times CT} \right) \times 100\). As the total work content does not change for a problem to be solved, LE depends on the number of workstations opened and the cycle time determined. This paper proposes linear and nonlinear models to maximize the LE simultaneously minimizing these two conflicting objectives (CT and NS) which are usually handled independently.

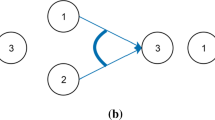
The precedence relationship constraints in the DLBP is divided into two groups: AND precedence relation and OR precedence relation. Note that the directed arrows in the figure represent the AND precedence relation, while the arc between the arrows represents the OR precedence relation. For example, either task 2 or task 3 must be completed to initialize task 1 or task 9. Therefore, the precedence relationships in DLBP are much more complex than that in the ALBP. That is because there are only AND precedence relationships in ALBP, whereas there are AND precedence, OR precedence and complex AND/OR precedence relationships in DLBP (Güngör and Gupta 2002).

2.1 Mathematical model

A mixed-integer nonlinear model is presented here to solve the DLBP-E with multi-manned workstations with the aim of maximizing the line efficiency as a primary objective. Type-E problems differ from Type-I and Type-II by optimizing the two conflicting objectives, CT and NS. Recall that NS is minimized (given CT) in Type-I problems, and CT is minimized (given NS) in Type-II problems. In DLBP-E, the problem also considers complex AND/OR relationships (as explained in the previous subsection) different from traditional assembly.

The objectives of removing hazardous and highly-demanded parts in the earlier workstations are also considered as the secondary and tertiary objectives.

Notation

i, h

The task index, \(i,h = 1,2, \ldots ,n;\) and \(i,h \in I\)

j, g

The workstation index \(j,g = 1,2, \ldots ,K;\) and \(j,g \in J\)

ti

The processing time of task i

hazi

1, if the part to be removed by task i is hazardous; 0, otherwise.

di

The demand for the part to be removed by processing task i

\(\varphi\)

A very large positive number

ORP

The set of tasks that have OR predecessors

ORi

The set of tasks preceding task i with OR precedence relation

ANDi

The set of tasks preceding task i with AND precedence relation

RP

The maximum number of operators that can be allocated to a workstation (in other words, the upper value that the capacity of a workstation can be replicated)

T

The sum of processing times of tasks to be disassembled, \(T = \sum\nolimits_{i \in I} {t_{i} }\)

Decision variables

Zj

The number of operators assigned to workstation j; 0, if workstation is not opened (\(Z_{j} \ge 0\))

Xij

1, if task i is assigned to workstation j; 0, otherwise

CT

cycle time (\(CT \ge 0\))

Objective function (model-NL)

$$\hbox{max}\, f_{1} = T/\left( {\mathop \sum \limits_{j \in J} Z_{j} \times CT} \right) \times 100.$$
(1)
$$\hbox{max}\, f_{2} = 1/\mathop \sum \limits_{i \in I} \mathop \sum \limits_{j \in J} haz_{i} \cdot X_{ij} .$$
(2)
$$\hbox{max}\, f_{3} = 1/\mathop \sum \limits_{i \in I} \mathop \sum \limits_{j \in J} d_{i} \cdot X_{ij} .$$
(3)

Constraints

$$\mathop \sum \limits_{j \in J} X_{ij} = 1;\quad \forall i \in I.$$
(4)
$$\mathop \sum \limits_{i \in I} t_{i} \cdot X_{ij} \le CT \times Z_{j} ;\quad \forall j \in J.$$
(5)
$$X_{ij} \le \mathop \sum \limits_{g < j} X_{hg} ;\quad \forall i \in I; \;\forall j \in J; \;\forall h \in AND_{i} .$$
(6)
$$X_{ij} \le \mathop \sum \limits_{g < j} \mathop \sum \limits_{{h \in OR_{i} }} X_{hg} ;\quad \forall i \in ORP;\; \forall j \in J.$$
(7)
$$Z_{j} \le RP;\quad \forall j \in J.$$
(8)
$$X_{ij} \in \left\{ {0,1} \right\};\quad i \in I;\; \forall j \in J.$$
(9)

The model hierarchically optimizes the objective functions given in Eqs. (1)–(3). The first objective function, \(f_{1}\) given in Eq. (1), relates to the maximization of LE. If there is more than one solution with the same LE value, the model aims to maximize \(f_{2}\) which corresponds to the objective of removing hazardous parts at earlier workstations. Another objective, \(f_{3}\), is considered when there is more than one solution with exactly the same \(f_{1}\) and \(f_{2}\) objectives.

Constraints are given in the Eqs. (4)–(9). Equation (4) ensures that each task is assigned to exactly one workstation while Eq. (5) satisfies the capacity constraint. Equations (6) and (7) relates to AND precedence and OR precedence relations, respectively. Equation (8) limits the number of workers that can be assigned to each workstations and Eq. (9) is the sign constraint.

Note that this model is somehow unbounded in terms of the ‘total’ number of workers utilised across the line. Therefore, the following constraint can also be added to the model to directly restrict the total number workers/operators allocated to all workstations.

$$\mathop \sum \limits_{j = 1}^{K} Z_{j} \le \delta$$
(10)

where \(\delta\) is the upper bound on the total number of workers allocated across the line. If this constraint is not utilised, the upper bound for the total number of operators will naturally be \(K \times RP\).

2.2 Numerical example

A numerical example is provided here for the illustration of the introduced DLBP-E with multi-manned workstations. The precedence relationship diagram of the example given in Fig. 1 is considered together with the database given in Table 1. In the table, the removal times, hazardous conditions and demands for parts are presented.

Fig. 1
figure 1

The precedence relationship diagram of the 10-part example

Full size image
Table 1 The database for the 10-part example
Full size table

If the problem is solved in Type-I form (where CT is constant and NS is minimized) as in the literature under the cycle time constraint \(CT = 40\), the optimum solution of the problem requires 5 workstations. That corresponds to a line efficiency of \(LE = 86.5\%\). Figure 2a presents the allocation of tasks to the workstations for this solution. Note that multi-manned stations are not allowed in this solution. In this condition, the number of operators is the same as the number of workstations.

Fig. 2
figure 2

The comparison of the solutions: a the solution obtained when the problem is solved in Type-I form; The solutions obtained with the proposed model with b single-manned workstations (\(RP = 1\)) and c multi-manned workstations (\(RP = 2\))

Full size image

When the problem is solved using the proposed model (assuming that \(RP = 1\)), it is seen that the optimal CT and NS combination is found as \(CT = 39\), \(NS = 5\), which corresponds to a LE value of \(LE = 88.71\%\). The allocation of tasks to workstations is given in Fig. 2b. For the purpose of comparison with the solution given in Fig. 2a, this solution is obtained under the condition that only one operator can operate in each workstation (single-manned workstations).

The problem is also solved allowing that more than one worker can be allocated to the same workstation (\(RP = 2\)) and limiting the upper value for the total number of workers to 6, i.e. \(\delta = 6\). The solution obtained with \(LE = 90.10\%\) is presented in Fig. 2c. Notice that the number of operators (OP) needs to be considered in the calculation of LE as multi-manned stations are allowed.

As seen from the figure, two operators are allocated to the workstations WS2 and WS4 (multi-manned workstations). In one hand, the cycle time is reduced from 39 to 32 in comparison to the solution obtained when only one operator is allowed to operate in each workstation (\(RP = 1\)). On the other hand, the number of operators is increased from 5 to 6. However, the LE value of the solution is improved by 4% compared to the solution obtained in Type-I form. Furthermore, another solution with an even better value of LE (\(LE = 95.05\%\)) could be obtained for the same problem if the value of \(\delta\) was set to 7, i.e. \(\delta = 7\). This improvement can be larger in the large-sized problems containing tens or hundreds of tasks. The efficiency of the proposed model in solving the DLBP-E can be clearly seen from this numerical example.

3 Iterative MILP model

The nonlinear model proposed in the previous section is very effective and solvable for the DLBP-E with multi-manned workstations. However, due to the complexity of the studied problem, it becomes unsolvable for the large-sized (even some medium-sized) problems. For this purpose, the problem is levered to a Type-I DLBP considering a constant cycle time value and solved iteratively.

The model presented below (called Model-L) is solved iteratively increasing the cycle time value by CTinc in each subsequent iteration.

Objective function (model-L)

$$\hbox{min}\; f_{4} = \mathop \sum \limits_{j \in J} Z_{j}$$
(11)

\(\hbox{min}\;f_{2}\text{ and min}\, f_{3}\), see Eqs. (2)–(3) in Sect. 2.1.

Constraints

Equations (4)–(9) in Sect. 2.1.

The primary objective of the proposed model is to minimize the number of operators. When there is more than one solution with the same value of \(f_{4}\), secondary and tertiary objectives are considered hierarchically (\(f_{2}\) and \(f_{3}\), respectively, as in Sect. 2.1).

Figure 3 outlines the basic solution building procedure of the proposed iterative MILP method (abbreviated with iMILP). The algorithm starts with importing problem data and initializing all problem specific parameters. The best solution indicators are also initialised and CT is set to its lower bound, CTLO (\(CT \leftarrow CT_{LO}\)). The problem is solved using Model-L and the performance measures (LE, \(f_{2}\) and \(f_{3}\)) of the obtained solution are compared to the current best values (\({\text{LE}}^{*}\), \(f_{2}^{*}\) and \(f_{3}^{*}\)) hierarchically and the current best solution is updated if a better solution is found (Note that LE is calculated using f4). CT is increased by CTinc (\(CT \leftarrow CT + CT_{inc}\)) and this cycle continues until CT reaches to CTUP. The best CT value which gives the best solution (and so the highest line efficiency) is reported and the algorithm is terminated.

Fig. 3
figure 3

The flow-chart of the proposed procedure (iMILP)

Full size image

For the demonstration of the solution mechanism of the proposed model, a numerical example is provided below and solved using the iMILP method. This example relates to a disassembly process of 25-part cellular phone (Kalayci and Gupta 2013b). Figure 4 presents the precedence relationship diagram of the example problem. As seen from the figure, a dummy task (A1) is created to have a better representation and increase readability. Note that no OR relationship exists in the example. The removal times of parts (task times), their hazardous conditions and demands are also provided in Table 2. Recall that the columns named Hazardous and Demand correspond to the calculation of objective values \(f_{2}\) and \(f_{3}\).

Fig. 4
figure 4

The precedence relationship diagram of the 25-part example (Kalayci and Gupta 2013b)

Full size image
Table 2 The database for the 25-part example (Kalayci and Gupta 2013b)
Full size table

The problem is solved using the iMILP method and the results are plotted in Fig. 5 to depict the convergence of the LE as well as the number of stations (which is equivalent to OP as there is only one operator in each workstation). The value for the replication parameter is set to \(RP = 1\), which indicates that at most one operator can be allocated to each workstation.

Fig. 5
figure 5

The change in the line efficiency and the number of operators across the cycle time

Full size image

As seen from Fig. 5, the values for CTLO and CTUP are 18 and 27, respectively. The increment value is assumed to be \(CT_{inc} = 1\) to check each possible CT value and to have a well-balanced line. In fact, CTLO and CTUP should be determined based on the demand and the number of operators allowed. On one hand, the cycle time must be small enough to meet the demand with no delay. On the other hand, it must be large enough not to require more operators than that available. It should also be noted here that CTLO must not be lower than the maximum of the part removal times (no parallel stations or multi-manned stations are allowed). Regarding the example provided here, the best LE value (96.88%) is obtained for the CT and OP combination of 20 and 8, respectively. While the cycle time increases, OP reduces gradually, which results in different LE values based on the CT–OP combinations.

4 Computational experiments

A computational study is conducted in this section to demonstrate the capability of the proposed models in solving the benchmarks in the literature. For this aim, five sets of test instances in varied sizes have been derived from the literature, i.e. P8 from Kalayci and Gupta (2014), P10 and P25 from Kalayci and Gupta (2013b), P10-OR from Avikal and Mishra (2012), and P47A, P47B and P47C from Kalayci et al. (2015). Note that any sequence-dependent time increase is ignored as this is not the case in the problem studied in the current work. Some modifications have also been done to have test instances with larger number of tasks. Namely, P94-1, P94-2 and P94-3 have been obtained by combining the precedence relationships of test problems P47A–P47A, P47A–P47B and P47A–P47C, respectively.

Tests have been performed in two phases. First of all, the proposed MINLP model was coded in General Algebraic Modeling System (GAMS) and solved via the embedded BONMIN solver on a PC equipped with Intel® Core™ i7-6700HQ CPU @2.60 GHz and 16 GB of RAM. This model was used to solve all test problems to optimality under various settings. Secondly, the proposed iMILP method has been coded in GAMS and solved via CPLEX iteratively using the flow control commands within the specified range of cycle time (CTLO and CTUP) to solve all test problems again.

Table 3 presents the test problems and its results obtained under various constraints. This table makes it possible to make an observation on how balancing a problem in Type-E form helps improve the line efficiency. The column Type-I presents the optimal solutions of the problems obtained under a constant cycle time (recall that Type-I formulations aim to minimize the number of workstations given the cycle time). Each problem was solved under three different cycle time constraints and the results have been reported for each case. The columns MINLP and iMILP present the optimal solutions obtained under two conditions: single-manned and multi-manned workstations (see the columns RP = 1 and RP = 2, respectively). While there are no CTLO and CTUP parameters used in the MINLP model, these values were used as a boundary for the value of CT to sustain its applicability. Also note that the OP values in iMILP results correspond to the objective f4. The computational times required by each model has also been provided in the table.

Table 3 Comparison of the results for small and medium-sized cases
Full size table

The results in Type-I and single-manned MINLP (\(RP = 1\)) columns can be compared to investigate the effect of considering both CT and NS (or equivalent to OP) on the effort to maximize LE.

As seen from Table 3, the Type-E formulation helps maximize the LE by a significant margin. Let us consider P10 with 10 tasks and a total work content of \(T = 169\) time-units. In the form of Type-I, the problem has been solved under three different cycle time constraints (\(CT = 38\), \(CT = 40\) and \(CT = 50\)). The LE values of the solutions with 5, 5 and 4 workstations (or operators) are calculated as 88.94%, 84.50% and 84.50%, respectively. When the cycle time is increased from 40 to 50, the number of workstations reduces from 5 to 4. Therefore, the total time allowed to complete all part removals with 169 time-units remains the same (which is 200 time-units). That leads to a line efficiency of \(LE\left( \% \right) = 84.5\%\). When the same problem is solved using the MINLP model, the line efficiency increases to 93.88% and 99.41% for the single-manned and multi-manned conditions, respectively. That indicates the superiority of the Type-E model.

When the results in the columns \(RP = 1\) and \(RP = 2\) are compared, it is seen that allowing more than one operator in the same workstation contributes to highly utilised workstations. This is mainly because of the increased number of combinations to assign tasks to workstations. The possibility of duplicating the capacity of a workstation provides more opportunity to assign tasks in such a way that idle times are minimized. The minimization of idle times yields increased line efficiency (as the total work content is the same).

The comparison of results reported in MINLP and iMILP columns shows the advantage of the proposed iterative method even for medium scale problems. MINLP and iMILP obtained optimal solutions P8 (\(RP = 1\) and \(RP = 2\)), P10 (\(RP = 1\) and \(RP = 2\)), P10-OR (\(RP = 1\)) and P25 (\(RP = 2\)). However, it exceeded the designated time limit of 1800 s for problems P10-OR (\(RP = 2\)) and P25 (\(RP = 1\)) for which iMILP was able to obtain the optimal solutions with 99.42% and 96.87% LE values, requiring 48 s and 195 s, respectively.

Table 4 reports the results for the large-sized problems. The results reported in the iMILP column indicate that the proposed method achieves better solutions with higher LE(%) values. Regarding the 47-task problems (P47A, P47B and P47C), MINLP was unable to prove an optimal solution within the time limit given 1800 s. On the other hand, iMILP returned better solutions with higher LE(%) values under both conditions (\(RP = 1\) and \(RP = 2\)) while not exceeding the 1800 s time limit.

Table 4 Comparison of the results for the large-sized cases
Full size table

Notice that MINLP was unable to get even a feasible solution for P94-1, P94-2 or P94-3 within the time limit, set to 2400 s. That was due to the increase in the number of tasks and so the search space. However, when \(RP = 1\), iMILP has reported efficient solutions within reasonable computation times. When multi-manned stations were allowed (\(RP = 2\)), the method required more computational effort. It was terminated when the computation time has reached to 2400 s and the best solution was reported. The results are still efficient when compared to single-manned solution, the same for P94-1 and very close for P94-2 and P94-3. Consequently, the results reported by iMILP clearly outperforms those reported by MINLP for the test problems solved.

Figure 6 presents the change in the LE and OP across the changing values of CT when solving P47C. The cycle time starts from CTLO and increases by CTinc until it reaches to CTUP.

Fig. 6
figure 6

The convergence of the iMILP model for P47C when a RP = 1 and b RP = 2

Full size image

In Fig. 6a, the problem is solved assuming that only one operator may work in each workstation (\(RP = 1\)). As seen from the figure, the cycle time is alternated between 112 and 163 time-units, with an increment value of three. Note that CTLO is higher than the maximum of the part removal times (which is 110) as multi-manned workstations is not allowed in this case [please refer to Kalayci et al. (2015) for the detailed data on the part removal times]. The highest efficiency (98.86%) is attained with 7 operators with a cycle time value of 151 time-units. There also are other high efficiencies with the cycle time values of 118 and 133, as seen from the figure (see the peak LE points). Obviously, the decision maker may also pick one of these alternative near-optimal solutions considering the possible highest and lowest speeds of the line (determined by CT) as well as the number of operators (or workstations as \(RP = 1\)) that the solution requires. For example, if the cycle time cannot be lower than 115 and higher than 135 due to the organizational strategies, the best CT and OP combination is \(CT = 118\) and \(OP = 9\) giving the highest value of \(LE = 98.40\%\) within the feasible range of CT. On the other hand, if the company intends to utilise at most 8 operators, then the best suitable option for this case is \(CT = 133\) and \(OP = 8\) giving the highest value of \(LE = 98.21\%\) within the solutions requiring at most 8 operators (keeping in mind that CT is lower than 135).

Figure 6b depicts the change in the LE and OP values for P47C as the cycle time is increased by \(CT_{inc} = 3\) within the bounds of \(CT_{LO} = 58\) and \(CT_{UP} = 163\). Note that multi-manned stations are considered in this case allowing the utilization of at most two operators in a workstation (\(RP = 2\)). Therefore, the value of CTLO must be equal to or larger than the half of the maximum part removal times. The best LE value is acquired with \(CT = 70\) requiring 15 operators (\(OP = 15\)). However, if the decision maker would like to utilise 12 operators at maximum, the best solution would be obtained when CT = 88 resulting in an efficiency of \(LE = 98.96\%\). These examples clearly show the importance and practical relevance of the proposed approach.

Regarding the managerial impacts of the work, the alternative combinations and their solutions are particularly important to decision makers in the industry. In the Type-I form, the decision maker (usually the line manager) needs to accomplish many trials to have a feasible as well as better balanced line configuration. Nevertheless, this effort will usually result in a feasible solution, but usually not the optimum in terms of the line efficiency. On the contrary, using the Type-E model enables the line manager pick the most suitable cycle time-number of operators (or workstations) combination to maximize the line efficiency. The decision maker must ensure that the cycle time must not be very large so that the customer demand is met on time. On the other hand, reducing the cycle time will require a greater number of operators to complete the tasks within the cycle time. Thus, the models and methodology proposed in this work helps the decision maker optimize the efficiency of the line while satisfying the organizational and capacity related considerations. So that the managers will be able to increase the efficiency of their systems using their existing resources more efficiently.

5 Conclusions and future research

Despite the increasing attention on the DLBPs recently, the problem of optimizing both cycle time and number of workstations (referred to as Type-E) has not been dealt in the literature. Furthermore, it was shown in the assembly line balancing literature that the possibility of allocating more than one operator to a workstation helps increase the line efficiency. However, the utilization of multi-manned workstations has not been investigated in the DLBP literature. As a pioneering attempt in this field, this research models and solves the DLBP-E with multi-manned workstations. A MINLP model is developed for the maximization of line efficiency (minimizing both cycle time and number of workstations/operators) as the primary objective. Due to the nature of the DLBPs, the secondary and tertiary objectives are also integrated into the model to remove hazardous and highly demanded parts at earlier stations as possible. A numerical example is shown to describe the problem and its optimal solutions are given under various conditions comparatively. As the nonlinear model falls short in solving the large-scale instances, it was levered to a linear model and embedded into an iterative algorithm to have timely-manner efficient solutions. The computational tests conducted clearly demonstrates that balancing disassembly lines considering the Type-E objective provides superior performance over Type-I in terms of maximizing the line efficiency with alternative combinations of cycle time and number of operators. It was also observed from the results of the computational study that allowing the utilization of multi-manned workstations (instead of single-manned workstations) increases the efficiency of the line significantly.

As there is no research on Type-E DLBP in the literature, no result exists to directly compare the solutions obtained in this work. That is one of the basic limitations of this work. Another limitation is the lack of real data to test the performance of the proposed models. This work can be extended in several ways. First of all, the models proposed in this work can be easily modified and applied to various line configurations, including U-shaped lines, two-sided lines and parallel lines. Secondly, heuristics and metaheuristics can be developed to solve even larger sized problems consisting of hundreds of jobs. Last but not least, model variations can be considered and the Type-E model can be applied to a mixed-model disassembly line.