Optimizing utilization in cellular radio networks using mobility data

Abstract

The main resource for any telecom operator is the physical radio cell network. We present two related methods for optimizing utilization in radio networks: Tetris optimization and selective cell expansion. Tetris optimization tries to find the mix of users from different market segments that provides the most even load in the network. Selective cell expansion identifies hotspot cells, expands the capacity of these radio cells, and calculates how many subscribers the radio network can handle after the expansions. Both methods are based on linear programming and use mobility data, i.e., data defining where different categories of subscribers tend to be during different times of the week. Based on real-world mobility data from a region in Sweden, we show that Tetris optimization based on six user segments made it possible to increase the number of subscribers by 58% without upgrading the physical infrastructure. The same data show that by selectively expanding less than 6% of the cells we are able to increase the number of subscribers by more than a factor of three without overloading the network. We also investigate the best way to combine Tetris optimization and selective cell expansion.

1 Introduction

The main resource for any telecom operator is the physical radio cell network. The potential revenue of the network is in most cases proportional to the number of subscribers that can use it without suffering from quality problems due to overloaded cells. The mobility pattern of the subscribers, i.e., where they tend to be during different times of the week, affects the load in the network. Operators want to have an even geographical spread of subscribers during all hours of the week, because then all cells are equally loaded all the time. The initial planning of a cellular network tries to predict the mobility pattern of subscribers by having a large number of small cells in city centers, sports arenas, and other places where one can expect a high density of subscribers during certain time periods.

The marketing department of a telecom operator normally divides the market into user segments, e.g., young adults, families, and business men/women. One reason for dividing the market into such segments is that different marketing campaigns can target these groups separately. Different segments have different mobility patterns, e.g., business people tend to be in the downtown area during the day, and young adults tend to be at schools or universities. If subscribers from one segment tend to be at different locations than subscribers from another segment, then these two segments would be a good and complementary mix from an infrastructure utilization point of view. If we know the average mobility pattern for subscribers in such segments, this information could be used to find a mix of subscriber segments that maximizes the utilization of the radio network. We will use the term Tetris optimization (the name is inspired by the famous game where one combines complementary shapes) for the process of finding a mix of subscriber segments that maximizes the utilization of the radio network. The main idea behind Tetris optimization is to have a revenue-based strategy when attracting subscribers. The user segments that the marketing department uses are not selected with Tetris optimization in mind; the purpose of these segments is to improve the understanding of the appeal of the telecom operator’s services to different market segments. However, it turns out that these segments also represent different user behavior, and our results show that these differences can be combined in a complementary way, thus reducing the maximum load in the network. This is a new aspect of user segments that we expect will affect marketing strategies.

If the mobility patterns of the subscribers are known, we could also use another method to optimize the infrastructure utilization. That approach is to do selective expansion of the radio network based on observed hotspots, i.e., one can insert new radio equipment and split a heavily loaded cell into smaller cells, thus making it possible to increase the number of subscribers without risking quality problems due to overloaded cells; we call this method selective cell expansion.

We use real mobility data from the telecom operator Telenor. The data represent one week for a region in Sweden. The mobility data are split into 5-min intervals. For each such interval, the data identify the cell corresponding to each subscriber. The subscribers are grouped into six segments by the marketing department. Based on this data we evaluate the Tetris optimization and selective cell expansion separately and in different combinations. Tetris optimization makes it possible to improve the network utilization without additional investment in the physical infrastructure. Selective cell expansion enables informed cost-revenue decisions when considering additional investment in the cellular network.

The rest of this paper is organized as follows. Section 2 discusses related work. In Sect. 3 the mobility data format is described, and some assumptions are formulated. Section 4 describes the two optimization methods, with a small example to aid understanding. Section 5 presents the results, and Sect. 6 discusses the assumptions and generalizations. The conclusions of this study are drawn in Sect. 7.

2 Related work

The analysis of mobile traffic has become increasingly important. In Naboulsi et al. (2015) provide a survey of 200 studies using data collected by mobile operators. One of the findings is that typical measures of human mobility include the number of locations visited during a certain time period (usually an hour or a day), the travel distance during a certain time period, mobility predictability, and spatiotemporal regularity (i.e., users and user segments tend to follow patterns and visit the same locations during the same periods of the week) (Lu et al. 2013; Song et al. 2010). In fact, the users’ well-studied mobility predictability and spatiotemporal regularity make it relevant to define different mobility patterns for different user segments, which is an important prerequisite for our study. According to Naboulsi et al., mobility data have not been used for network optimization.

There are two areas of related work that are relevant for this study: base-station placement and other forms of infrastructure optimization similar to selective cell expansion (see Sect. 2.1 below), and geodemographic user segments such as those used by Tetris optimization (see Sect. 2.2 below). The Tetris approach, i.e., finding the optimal mix of subscribers from a utilization point of view, has not been tried before. Most of the papers dealing with optimizing the utilization of radio cell networks use very simplified assumptions about the load and user behavior. To the best of our knowledge, no published study on the optimization of cellular radio networks uses the kind of real-world user mobility data that we use.

2.1 Optimization of the physical infrastructure

The optimization of wireless radio cell networks is an important area that has been studied for a long time (Hurley 2002; Ibbetson and Lopes 1997; Mathar and Niessen 2000; Molina et al. 1999; Siqueira et al. 1997; Tutschku and Tran-Gia 1998; Tutschku 1998). In Amaldi et al. (2008) the authors investigate different mathematical programming models for deciding where to install new base-stations and how to select their configuration to find a trade-off between coverage and cost; similar problems have been addressed in Yang et al. (2007) and Amaldi et al. (2006). The concept of force fields, motivated by the physics of multiple particles in a closed system, has also been used for optimizing base-station placement (Richter and Fettweis 2012).

Optimizing cell planning in modern radio networks with mixed cell sizes (i.e., smaller cells in areas with higher subscriber density) is a challenging problem. In Valavanis et al. (2014) and Athanasiadou et al. (2015), the authors investigate how genetic and other optimization algorithms can be used to find good locations for base-stations in networks with mixed cell sizes. The optimized planning of heterogeneous radio networks, where small cells are deployed within large macrocells, has been studied by Wang et al. (2015). The challenge in this case is to find a cost-effective way to satisfy the traffic requirements of the users.

The optimal placement of base-stations and relay stations in WiMAX (IEEE 802.16) networks has been studied by Yu et al. (2008). In that paper the authors define a model that uses integer programming to find the optimal physical locations of base-stations and relay stations in IEEE 802.16j networks. In Abichar et al. (2010) the authors extend the study by Yu et al. by allowing relay stations to be located several hops away from the base-station. An algorithm for optimal relay and base-station placement has also been developed by Islam et al. (2012); González-Brevis et al. 2011 have looked at base-station placement for minimal energy consumption.

Many of these studies use mathematical models and optimization techniques, but none of them use real-world mobility data, which is what we use in our study.

2.2 Geodemographic user segments

Geodemographic classification is used by almost all large consumer-oriented commercial organizations to improve their understanding of the appeal of their products and services to different market segments. Compared with conventional occupational measures of social class, postcode etc., geodemographic classifications typically achieve higher levels of discrimination. The two major segmentation systems are ACORN (a classification of residential neighbors) developed at CACI Limited and MOSAIC developed by CNN Marketing.

One of the reasons segmentation systems like ACORN are so effective is that they are created by combining statistical averages for both census data and consumer-spending data in predefined geographical units (Grubesic 2004). Originally developed for the UK, MOSAIC used some 400 items of small-area information to classify each of the 1.3 million UK postcodes into 61 mutually exclusive residential neighborhood types. The 61 categories were created using an expert algorithm that attempted to optimize the homogeneity of the categories with respect to the 400 input variables. The postcode descriptors are a powerful means to unravel lifestyle differences in ways that are difficult to distinguish using conventional survey research given limited sources and sample-size constraints (Webber 2009). The MOSAIC categories also correlate to diabetes propensity (Levy 2006), school students’ performance (Webber and Butler 2007), broadband access and availability (Grubesic 2004) and so on. Industries rely increasingly on geodemographic segmentation to classify their markets when acquiring new customers (Haenlein and Kaplan 2009).

Local versions of MOSAIC have been developed for a number of countries, including the USA, Australia, Sweden, Spain, Germany, and Norway. The main geodemographic systems are in competition with each other (e.g., Claritas, CACI, MOSAIC), and the exact details of the data and methods for generating lifestyle segments are not made public (Debenham et al. 2003). In this study, a MOSAIC-like segmentation system called Telenor Segments is used. Our work is based on Swedish MOSAIC and telecom data, i.e., it is based on international classification systems and the results are thus potentially transferable to other regions.

3 Mobility data and assumptions

The database provided by Telenor, and used in this study, contains historical location data from a region in Sweden with more than 1000 radio cells during 1 week with the user’s location registered every 5 min. This means that we have 7 × 24 × 12 = 2016 time slots of 5 min each. There are 27010 subscribers in the database.

The interesting fields in the main data file are:

• Subscriber ID

• Time slot (a number between 1 and 2016)

• Cell ID

The marketing department has identified six user segments (the Telenor Segments) that can be individually targeted via different marketing campaigns:

• 1. Corporate clients (139 subscribers in the database)

• 2. Cost aware (4003 subscribers in the database)

• 3. Modern John/Mary (5963 subscribers in the database)

• 4. Quality aware (5805 subscribers in the database)

• 5. Traditional (6007 subscribers in the database)

• 6. Value aware (5093 subscribers in the database)

These segments correspond to different lifestyles and habits. There is a separate file that maps each Subscriber ID to one of the six segments.

There are additional data about the physical location and address of each radio cell and about each subscriber in the MOSAIC format, but that information is not used in this study.

Assumption 1

The mobility pattern for the subscribers in a certain segment is predictable.

As discussed in the Related Work section, there are strong indications of the users’ mobility predictability and spatiotemporal regularity. We assume that increasing the number of subscribers in segment s₁ by a factor z results in an increase of the load generated by the subscribers in segment s₁ by a factor z for each cell and time slot. Of course, we do not know exactly how expanding the number of subscribers in a segment will affect the load in each cell at each point in time. To evaluate this assumption we created an alternative dataset by filtering out every second subscriber from each segment (thus halving the number of subscribers). To make it easier to directly compare the filtered and original datasets, we then duplicated each subscriber in the filtered dataset, thus obtaining a dataset with the same number of subscribers as the original dataset.

By comparing the performance of our optimization methods for the filtered and original datasets we can (to some extent) quantify the users’ mobility predictability and spatiotemporal regularity for the region in Sweden that we studied.

The financial return of a telecom network is a function of several parameters, including the number of subscribers, the services that these subscribers use, and their tariffs. Since there is no information available about the traffic consumption or the tariff, two additional assumptions are made.

Assumption 2

The revenues from the telecom network are proportional to the number of subscribers.

Assumption 3

The load in a cell at a certain time is proportional to the number of subscribers in that cell at that time.

4 Optimization methods

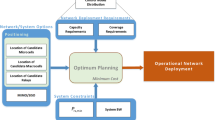
Figure 1 provides an overview of the input to and output from the two methods: Tetris optimization and selective cell expansion. The main input is the mobility data file, which is preprocessed into a matrix A, a vector s, and two parameters n and k, where n is the number of subscriber segments and k the number of time slots in the mobility data, i.e., in our case n = 6 and k = 2016. Both methods also need information about the network. The information about the network is represented by a capacity vector c and the number of radio cells p. The A matrix, the c, s and x vectors, the expansion factor β, and the “Keep all existing subscribers” parameter will be explained in detail below. Figure 1 shows that the two methods have almost the same inputs.

Fig. 1

Overview of the input to and output from the optimization methods

4.1 Tetris optimization

We seek to maximize the total number of subscribers y_j under the restriction that the number of subscribers in any cell during any 5-min interval does not exceed the capacity of the cell c_l. The total number of subscribers in segment j is denoted s_j; the s vector in Fig. 1 is defined as s = (s₁,…, s_n)^T. The number of subscribers belonging to segment j in cell l during time slot t seen from the database is denoted ã_l,t,j. The observed values ã_l,t,j are kept in a (kp)× n matrix A such that element a_i,j = ã_l,t,j, where i = l + (t − 1)p. The maximum subscriber capacity in cell l is denoted c_l; the c vector in Fig. 1 is defined as c = (c₁,…, c_p)^T.

There is a non-negative constant α_l,t,j such that

$$\ a_{l,t,j} = \alpha_{l,t,j} s_{j} \quad \forall\quad t \quad \forall\quad l$$

(1)

If there are y_j subscribers in segment j, we assume that the number of subscribers belonging to segment j in cell l during time slot t is (the number of subscribers must be an integer)

$$\lceil \alpha_{l,t,j} y_{j} \rceil$$

(2)

The integer linear programming formulation of the optimization problem thus becomes

$${\text{Maximize}}\,\mathop \sum \limits_{j = 1}^{n} y_{j}$$

(3)

$${\text{subject}}\,{\text{to}}\,\mathop \sum \limits_{j = 1}^{n} \lceil \alpha_{l,t,j} y_{j} \rceil \le c_{l}\quad \forall \quad l \quad \forall\quad t\,{\text{and}}$$

(4)

$$y_{j} \in {\mathbb{Z}},\text{ }y_{j} \ge 0 \quad \forall\quad j$$

(5)

In some cases we want to keep all existing subscribers, i.e., we do not want to reduce the number of subscribers in any segment. In that case we add the restriction

$$y_{j} \ge s_{j} \quad \forall \quad j$$

(6)

Integer linear programming problems are NP-hard (Gary and Johnson 1979), thus making them infeasible for large settings. The standard way to avoid the infeasibility problem is to relax the integer linear programming problem to a (normal) linear programming (LP) problem by removing the integer restriction (5). In our case we also have the integer requirement $\alpha_{l,t,j} y_{j}$ (2). This means that the integrality gap (i.e., the maximum ratio between the integer solution and of the relaxed problem) depends on the cell capacity $c_{l}$ and the number of segments n (4), i.e., in general a smaller $c_{l}$ and larger n give a larger integrality gap.

As discussed previously, based on subscribers’ mobility predictability and spatiotemporal regularity there are good reasons to expect that $\alpha_{l,t,j}$ is a relatively good approximation of the fraction of the total number of users in segment j that will be in cell l at time t. However, the subscriber behavior is not completely predictable so there will be some variations. Since we are considering a relatively small n, and since $c_{l}$ is in the order of 200 (see below), and since $\alpha_{l,t,j}$ are only approximations, we can relax the linear integer programming problem without losing any important information (below we will quantify the maximum error due to the relaxation). The relaxation is:

$${\text{Maximize}}\,\mathop \sum \limits_{j = 1}^{n} y_{j}$$

(7)

$${\text{subject}}\,{\text{to}}\,\mathop \sum \limits_{j = 1}^{n} \alpha_{l,t,j} y_{j} \le c_{l} \quad \forall\quad l\quad \forall \quad t\,{\text{and}}$$

(8)

$$y_{j} \in {\mathbb{R}},\text{ }y_{j} \ge 0\quad \forall\quad j$$

(9)

The relaxed problem provides an upper bound on the integer solution, which is obvious since $\alpha_{l,t,j} y_{j} \ge \alpha_{l,t,j} y_{j}$ and since the number of solutions grows when we relax the integer restrictions.

Theorem 1

A lower bound on the integer solution can be obtained by solving the problem

$${\text{Maximize}}\,\mathop \sum \limits_{j = 1}^{n} y_{j} - n$$

(10)

$${\text{subject}}\,{\text{to}}\,\mathop \sum \limits_{j = 1}^{n} \alpha_{l,t,j} y_{j} \le c_{l} - n \quad \forall\quad l \quad \forall\quad t\,{\text{and}}$$

(11)

$$y_{j} \in {\mathbb{R}},\text{ }y_{j} \ge 0 \forall\quad j$$

(12)

Proof

There are two relaxations: $\alpha_{l,t,j} y_{j}$ is replaced with $\alpha_{l,t,j} y_{j}$ in the restrictions, and the integer restriction on y_j is relaxed. It is clear that $\mathop \sum \nolimits_{j = 1}^{n} \alpha_{l,t,j} y_{j} < \mathop \sum \nolimits_{j = 1}^{n} \alpha_{l,t,j} y_{j} + n$, and it is also clear that relaxing the integer restriction can reduce the value of the target function by at most n, i.e., $\mathop \sum \nolimits_{j = 1}^{n} y_{j} - n$ (10) ($y_{j} \in {\mathbb{R}},\text{ }y_{j} \ge 0 \forall\quad j$ (11)) is smaller than $\mathop \sum \nolimits_{j = 1}^{n} y_{j}$ (3) ($y_{j} \in {\mathbb{Z}},\text{ }y_{j} \ge 0 \forall\quad j$ (5).

The proof of Theorem 1 shows how a feasible integral solution can be obtained. This is formulated in the following corollary.$\square$

Corollary 1

If$y_{j} \left( {j = 1 \ldots n, y_{j} \in {\mathbb{R}}, y_{j} \ge 0} \right)$is the solution to the LP problem in Theorem 1, then$y'_{j} = y_{j}$is a feasible (but not necessarily optimal) solution to the integer problem defined in (3)–(5).

In Sect. 5 we will see that for most scenarios we have the same c_l in all the restrictions, and that c_l is of the order of 200. In Sect. 5 we will also see that the maximum value of the target function is of the order of tens of thousands. This means that the effect of subtracting n (i.e., 6) from the target function $\left( {\mathop \sum \nolimits_{j = 1}^{n} y_{j} } \right)$ is a fraction of a percent, i.e., this effect is small and can be ignored. The effect of subtracting n from c_l in the restrictions can be understood by considering the following argument: Let $\gamma = c_{l} /\left( {c_{l} - n} \right)$. If we multiply the target function (10) and the restrictions (11) by γ, and let γy_j= x_j we get:

$${\text{Maximize}}\,\mathop \sum \limits_{j = 1}^{n} x_{j}$$

$${\text{subject}}\,{\text{to}}\,\mathop \sum \limits_{j = 1}^{n} \alpha_{l,t,j} x_{j} \le c_{l} \quad \forall\quad l \quad \forall\quad t\,{\text{and}}$$

$$x_{j} \in {\mathbb{R}},\text{ }x_{j} \ge 0 \quad \forall\quad j$$

which is identical to the relaxed version of the problem (7)–(9), which is the upper bound on the integer solution. This means that the effect of subtracting n from c_l in the restrictions is that the value of the target function is reduced by a factor $c_{l} /\left( {c_{l} - n} \right)$. If c_l is of the order of 200 and n = 6, we see that the difference between the lower and upper bounds on the integer solution is approximately 3%.

In our case n = 6, there are millions of restrictions. Reducing the number of restrictions that we need to consider would make it faster and easier to perform heuristic searches for near-optimal integer solutions. In Appendix A we present a method that significantly reduces the number of restrictions that we need to consider.

As discussed before, our optimization model is based on the assumption that the number of subscribers of a segment in a particular cell at a particular point in time will scale with the total number of subscribers in that segment. However, since this scaling is of course not exact, and since the difference between the (relaxed) lower and upper bounds on the integer solution is in our case only 3%, it suffices to use the relaxed solution (the upper bound) as an approximation. When we solve the relaxed LP problem, we use a slightly different formulation and introduce scaling factors x_j for each subscriber segment; the x vector in Fig. 1 is defined as x = (x₁ ,…, x_n)^T. We optimize x in our LP problem. The existing mix of subscribers corresponds to x_j = 1 (1 ≤ j ≤ n). If we change some x_j, we assume that the number of subscribers in each cell at each point in time will change proportionally.

There are kp restrictions (one restriction for each cell and time slot), and we need to multiply c by a $\left( {kp} \right) \times k$ matrix B to get a capacity vector of length kp (I_p is the identity matrix of size p)

$${\mathbf{B}} = \overbrace {{\left( {{\mathbf{I}}_{p} , \ldots ,{\mathbf{I}}_{p} } \right)^{\text{T}} }}^{k}$$

(13)

Given this notation and assumptions, the LP problem becomes:

$${\text{Maximize}}\,{\mathbf{s}}^{\text{T}} {\mathbf{x}}$$

(14)

$${\text{subject}}\,{\text{to}}\,{\mathbf{Ax}} \le {\mathbf{Bc}}\,{\text{and}}$$

(15)

$${\mathbf{x}} \ge 0$$

(16)

There are more than 1000 radio cells in the region, so there are more than two million restrictions.

We may want to keep all existing subscribers, i.e., we do not want to reduce the number of subscribers in any segment (see Fig. 1). In that case we add the restriction

$${\mathbf{x}} \ge 1$$

(17)

During Tetris optimization the capacity $c_{l}$ is the same for all cells (we use different $c_{l}$ for different cells when we combine Tetris optimization with selective cell expansion). The capacity is selected as the maximum number of subscribers seen in any cell during any 5-min time slot. For the full dataset $c_{l} = 165$, and for the filtered dataset $c_{l} = 210$. As discussed before, the filtered dataset contains two copies of each subscriber. This reduces the variation in the dataset and increases the hotspots. As a consequence, a larger cell capacity is needed to handle the filtered dataset. The increase in the hotspots can be understood by the following reasoning: Consider the case where we have only one copy of each subscriber in the filtered dataset, i.e., we have half of the subscribers in the full dataset. Look at the cells and time slots with the highest number of subscribers (the hotspots). In the filtered dataset we simply multiply the number of subscribers by two in all the time slots, including the hotspots. In the full dataset we add the other half of the subscribers to each time slot. If the mobility pattern in the two halves were identical, we would get the same result for the filtered and full datasets. However, there are of course some variations. If the mobility patterns were completely independent in the two halves, it would be like throwing two dice and adding up the sum for each combination of a cell and a time slot for the full dataset, and throwing one die and multiplying the result by two for the filtered dataset. The hotspots correspond to the maximum value, and it is clear that the probability of getting the maximum value (12 for two normal dice) is higher if we only throw one die and multiply that value by two. Since the mobility pattern in the two halves of the subscribers is similar but not identical, we have, for the full dataset, a situation that is somewhere between throwing two dice and throwing one die and multiplying by two. The effect of this is that, compared to the full dataset, there is a slight increase in the hotspots in the filtered dataset.

If we are willing to decrease the number of subscribers in some segments, i.e., if we do not have restriction (17), the relative gain of Tetris optimization is not affected by the absolute value of $c_{l}$. If we have different values of $c_{l}$ for different cells, which we will explore in Sect. 5.3, the gain of Tetris optimization may be affected, since different restrictions may become active. However, even when we have different values of $c_{l}$ for different cells, it is only the ratios between these values, and not the absolute values, that affect the gain of Tetris optimization if we do not have restriction (17). If we add restriction (17), the absolute cell capacity $c_{l}$ affects the gain of doing Tetris optimization, e.g., for $c_{l} = 165\forall l$ (the minimum cell capacity that can handle the current set of subscribers) we get no gain for the full dataset, but for larger $c_{l}$ we will see a gain.

4.2 Small example

Consider a small example with two cells, two subscriber segments and three time slots (p = 2, n = 2, and k = 3). The ã_l,t,j values are shown in Table 1. The total number of subscribers in segment 1 is 60, and the total number of subscribers in segment 2 is 40 (s = (60, 40)^T). N.B. For some time slots and some segments, the sum of the subscribers can be smaller than s = (60, 40)^T. This means that some subscribers may be inactive during some time intervals. The capacity of both radio cells is 200, i.e., c = (200, 200)^T.

The Tetris optimization problem becomes:

• Maximize 60x₁+40x₂.

• The LP problem has np = 6 restrictions:

• for t₁, cell 1: 40x₁ ≤ 200,

• for t₁, cell 2: 20x₁+20x₂ ≤ 200,

• for t₂, cell 1: 40x₁ ≤ 200,

• for t₂, cell 2: 40x₂ ≤ 200,

• for t₃, cell 1: 25x₁+25x₂ ≤ 200,

• for t₃, cell 2: 10x₁+15x₂ ≤ 200, and ${\mathbf{x}} \ge 0$

That is, we have the following:

$${\mathbf{A}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {40} & 0 \\ {20} & {20} \\ {40} & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & {40} \\ {25} & {25} \\ {10} & {15} \\ \end{array} } \\ \end{array} } \right),\;{\mathbf{Bc}} = \left( {\begin{array}{*{20}l} 1 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill \\ 1 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill \\ 1 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {200} \\ {200} \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} {200} \hfill \\ {200} \hfill \\ {200} \hfill \\ {200} \hfill \\ {200} \hfill \\ {200} \hfill \\ \end{array} } \right)$$

Solving this LP problem yields the optimal x = (5, 3)^T, corresponding to ${\mathbf{s}}^{\text{T}} {\mathbf{x}}$ = 420

4.3 Selective cell expansions

The capacity of a radio cell can be expanded by splitting an old cell into two or more new cells. Cell splitting is important for network densification, which is a key mechanism for 5G networks (Bhushan et al. 2014). When we split a cell l we do not create two new cell restrictions in our LP model; instead we assign a new larger value to the capacity. We do that by multiplying the cell capacity by an expansion factor$\beta$

$$c_{l} \leftarrow \beta c_{l}$$

(18)

If we split an old cell into two new cells and are able to do a perfect split, half of the subscribers in the old cell will end up in each of the two new cells; this corresponds to $\beta = 2$. A split would probably be able to cut the geographical area covered by the old cell into two (almost) equally sized cells. During the peak hours there are probably active phones in almost all parts of the cell, i.e., one could argue that splitting the load during the peak periods into half is optimistic, but not completely unrealistic.

If on the other hand we make the pessimistic assumption that the load in a certain part of a cell is totally unrelated to the size of that part, the fraction of subscribers in one of the halves would be a random variable with a uniform distribution between 0 and 1. This would mean that after the split, the average value for the most heavily loaded cell would be 3/4 of the original load; this corresponds to $\beta$ = 4/3.

Unless explicitly stated otherwise, and to strike a compromise between the optimistic ($\beta$ = 2) and the pessimistic ($\beta$ = 4/3) assumptions, we assume that the number of subscribers in each of the two new cells is at most 2/3 of the number in the old cell. The 2/3 assumption corresponds to $\beta$ = 3/2.

Obviously, expanding a cell affects the capacity in all the time slots. This means that expanding cell number k corresponds to multiplying the cell capacity c_l by 3/2 (using the 2/3 assumption) in our LP model. When doing pure cell expansions we do not want to do Tetris optimization, i.e., we want to increase the number of subscribers but not change the mix of subscribers. To retain the mix of subscriber segments we add the restriction

$$x_{1} = x_{2} \ldots = x_{n}$$

(19)

when $x_{1} = x_{2} \ldots = x_{n}$ the maximum number of subscribers, i.e., the value of the objective function max ${\mathbf{s}}^{\text{T}} {\mathbf{x}}$, is limited by some restrictions: the active restrictions. The capacity of the cell (cell l) corresponding to the first active restriction is then expanded, i.e., $c_{l} \leftarrow \beta c_{l}$. The restrictions are ordered based on the time-slot order, and for each time slot the restrictions are ordered based on the cell id (see the example in Sect. 4.2). The B matrix (13) ensures that the multiplication $c_{l} \leftarrow \beta c_{l}$ affects all the 2016 restrictions associated with the cell. The value of the objective function is calculated with the new c vector. It turns out that in most cases, the active restrictions are related to the same cell (there are 2016 restrictions for each cell), and in these cases there is only one expansion alternative. Moreover, if the active restrictions are related to more than one cell, we observed that the cell expansion order did not have a significant impact on the target value.

4.4 Example for cell expansions

Consider the example in Sect. 4.2. If we add the restriction x₁ = x₂, the optimal x = (4, 4)^T, which corresponds to ${\mathbf{s}}^{\text{T}} {\mathbf{x}}$ = 400. In this case the active restriction is for time slot t₃ and cell 1: 25x₁+25x₂ ≤ 200. If we expand cell 1 by multiplying the capacity by 3/2 we get c = (300, 200)^T and the following restrictions:

• for t₁, cell 1: 40x₁ ≤ 300,

• for t₁, cell 2: 20x₁+20x₂ ≤ 200,

• for t₂, cell 1: 40x₁ ≤ 300,

• for t₂, cell 2: 40x₂ ≤ 200,

• for t₃, cell 1: 25x₁+25x₂ ≤ 300,

• for t₃, cell 2: 10x₁+15x₂ ≤ 200,${\mathbf{x}} \ge 0,$ and x₁ = x₂

Solving this LP problem yields the optimal x = (5, 5)^T, corresponding to ${\mathbf{s}}^{\text{T}} {\mathbf{x}} = \varvec{ }$ 500. N.B. the active restrictions are related to cell 2 after the expansion of cell 1.

5 Results

The s vector and the A matrix are calculated from the mobility data file using a C++ program (see Fig. 1). The LP problem was solved with respect to x using an R program (Core Team 2015) and the Gurobi solver (2016).

5.1 Tetris optimization

As mentioned in Sect. 3, there are 27010 subscribers in both the full and the filtered datasets. In the full dataset, the cell capacity is set to 165 for all cells, which is the minimum cell capacity for handling the observed values. When solving the optimization problem, for the full dataset we get an objective function value of 42755 subscribers. This corresponds to a 58% increase in the number of subscribers using the same physical radio network (42755/27010 = 1.58). As discussed previously, the relative increase (58%) would be the same even if we assume that each radio cell has a capacity larger than 165. For instance, if we assume a cell capacity of 330, we get 2 × 27010 = 54020 subscribers in the unoptimized case and 2 × 42755 = 85510 subscribers after Tetris optimization.

In the case of the filtered dataset we get almost the same result after Tetris optimization: we get 42403 subscribers, which corresponds to a 57% increase (42403/27010 = 1.57).

For the full dataset x = (0, 0.13, 0, 1.45, 4.85, 0.92)^T. As a consequence, the optimized subscriber mix (i.e., the terms in the dot product ${\mathbf{s}}^{\text{T}} {\mathbf{x}}$) are:

• 1. Corporate clients (0 subscribers),

• 2. Cost aware (520 subscribers)

• 3. Modern John/Mary (0 subscribers)

• 4. Quality aware (8417 subscribers)

• 5. Traditional (29133 subscribers)

• 6. Value aware (4685 subscribers)

This means that the optimized mix for the full dataset is dominated by subscribers from the Traditional user segment; the optimal mix in the filtered dataset is very similar, and that mix is also dominated by the Traditional user segment. The fact that the optimized mix for the full and the filtered datasets are very similar shows that Assumption 1 (the mobility pattern for the subscribers in a certain segment is predictable) is valid in our case.

As discussed in Sect. 4, we may not want to remove existing users. If the radio network is close to its maximum capacity and we do not want to remove existing subscribers, the gain of adding more subscribers in a Tetris optimized way is small compared to just adding an equal proportion of subscribers from each segment. However, when there is much unused capacity in the network, the gain of adding more subscribers in a Tetris optimized way compared to increasing the number of users in each segment proportionally becomes larger even if we do not want to remove existing subscribers. When the unused capacity goes to infinity, the gain of adding more subscribers using Tetris optimization asymptotically approaches 58% (for the full dataset) or 57% (for the filtered dataset) from below.

5.2 Selective cell expansions

Figure 2 shows the number of subscribers as a function of the number of cell expansions. As discussed before, when doing cell expansion we add the restrictions x₁ = x₂ = x₃ = x₄ = x₅ = x₆ to our LP model. When doing multiple selective cell expansions, we use the updated c vector from the previous expansion as the input for the next expansion (see Fig. 1). In some cases multiple cells prevent us from adding more subscribers. This can be seen as flat segments in Fig. 2. The figure shows that doing 100 cell expansions increases the maximum number of users from 27,000 to more than 100,000 for both datasets when we use $\beta$ = 3/2. For $\beta$ = 2 and $\beta$ = 4/3 we see that the difference in terms of the maximum number of subscribers increases when the number of cell expansions increases. This is because for the lower expansion factors, more cells need to be expanded multiple times.

Fig. 2

The maximum number of subscribers as a function of the number of cell expansions for different expansion factors β. The solid line corresponds to β = 3/2, the dotted line below corresponds to β = 4/3, and the dotted line above corresponds to β = 2 (full dataset to the left and filtered dataset to the right)

A detailed analysis showed that for the full dataset and $\beta$ = 4/3, 56 cells were expanded. For $\beta$ = 3/2, the same 56 cells plus 5 new cells were expanded, i.e., in total 61 cells were expanded. For $\beta$ = 2, these 61 cells were expanded plus 16 new cells, i.e., in total 77 cells were expanded. There are more than 1000 cells in the network, and for expansion factor 3/2 we are able to increase the maximum number of users by more than a factor of three by expanding less than 6% of the cells.

5.3 Combining the two methods

Selective cell expansion and Tetris optimization are based on very similar inputs (see Fig. 1), and they both address network optimization. It is thus clear that network operators and similar stakeholders would like to combine the methods. We will evaluate four ways to combine the two optimization methods.

One way of combining the two methods is to first do Tetris optimization, and then do cell expansion with the mix of user segments obtained after the Tetris optimization. We evaluated this approach by first doing Tetris optimization, thus obtaining x = (0, 0.13, 0, 1.45, 4.85, 0.92)^T for the full dataset (see Sect. 5.1).

We now define elementwise multiplication of two vectors a◦b = c such that c_i= a_ib_i (often called the Hadamard product) and elementwise multiplication of a vector and a matrix a◦B = C such that c_j,i= a_ib_j,i. Given this notation, and the x vector obtained from Tetris optimization, we calculate

$${\mathbf{s}}'\varvec{ } \leftarrow {\mathbf{x}} \circ {\mathbf{s}}$$

(20)

$${\mathbf{A}}'\varvec{ } \leftarrow {\mathbf{x}} \circ {\mathbf{A}}$$

(21)

We then solve

$${\text{Maximize}}\,{\mathbf{s}}'^{\text{T}} {\mathbf{x}}$$

(22)

$${\text{subject}}\,{\text{to}}\,{\mathbf{A}}'{\mathbf{x}} \le {\mathbf{Bc}},$$

(23)

$${\mathbf{x}} \ge 0,\,{\text{and}}$$

(24)

$$x_{1} = x_{2} \ldots = x_{n}$$

(25)

This preserves the subscriber mix obtained after Tetris optimization (s′ represents that mix). We then do selective cell expansion in the same way as in Sect. 5.2, i.e., by identifying the cell associated with an active restriction and multiplying the capacity of that cell by β.

The green line in Fig. 3 shows the result of doing Tetris optimization followed by cell expansion, for the first 100 cell expansions. For β = 2 and β = 4/3 we see that the difference in terms of the maximum number of subscribers increases as the number of cell expansions increases. This is because for the lower expansion factors, more cells need to be expanded multiple times. A detailed analysis showed that for β = 4/3, 61 cells were expanded. For β = 3/2, the same 61 cells plus 6 new cells were expanded, i.e., in total 67 cells. For β = 2, these 67 cells were expanded plus 17 new cells, i.e., in total 84 cells.

Fig. 3

The maximum number of subscribers as a function of the number of cell expansions after initial Tetris optimization. The solid green line corresponds to β = 3/2, the dotted line below corresponds to β = 4/3, and the dotted line above corresponds to β = 2 (full dataset to the left and filtered dataset to the right). (Color figure online)

Figure 4 compares the effect of cell expansion (β = 3/2) with initial Tetris optimization (the green line) with the case where there is no initial Tetris optimization and β = 3/2 (the red line). The figure shows that the initial gain of doing Tetris optimization remains when the number of cell expansions increases.

Fig. 4

The maximum number of subscribers as a function of the number of cell expansions for β = 3/2. The green line shows the case with initial Tetris optimization (full dataset to the left and filtered dataset to the right). (Color figure online)

As discussed above, for cell expansions with no Tetris optimization (the red line in Fig. 4) the first 100 expansions affected 61 unique radio cells, and for cell expansion with Tetris optimization (the green line in Fig. 4) the first 100 expansions affected 67 unique radio cells. It turns out that 59 cells (out of the 61 and 67) were expanded for both cases.

Another way of combining cell expansion and Tetris optimization is to start with cell expansion and to perform Tetris optimization after a certain number of cells have been expanded. In this case we do normal Tetris optimization but use the updated c vector (see Fig. 1).

Figure 5 shows the effect of first doing cell expansion (the red line) and then doing Tetris optimization after every second expansion. Each Tetris optimization is indicated as a red circle. The gain of applying Tetris optimization after cell expansion is rather limited. This is because cell expansions evens out the load in the network, since the heavily loaded cells are expanded, thus limiting the effect of additional load balancing through Tetris optimization. Doing Tetris optimization followed by cell expansion (the green line) is better than doing cell expansion followed by Tetris optimization (the red circles). The green circles in Fig. 5 show the effect of doing one additional Tetris optimization after having expanded a number of cells after initial Tetris optimization; each final Tetris optimization is indicated as a green circle, and we have again done a final Tetris optimization for every even numbered expansion. The gain of doing a final Tetris optimization is small for the green line compared to the red line, which can be expected since the subscriber mix has already been optimized once (i.e., the green line starts with a Tetris optimization). Figure 6 shows the maximum number of subscribers as a function of the number of cell expansions for the most favorable case, which is Tetris optimization followed by cell expansions and then a final Tetris optimization. This means that the black line in Fig. 6 is a denser version of the green circles in Fig. 5; it is denser since we have now plotted the result for every cell expansion, not just for every second cell expansion as in Fig. 5.

Fig. 5

Cell expansions followed by Tetris optimization (red circles), compared to Tetris optimization followed by cell expansions and then a final Tetris optimization (green circles) (full dataset to the left and filtered dataset to the right). The red and green lines are the same as in Fig. 4. (Color figure online)

Fig. 6

Tetris optimization followed by cell expansions and then followed by a final Tetris optimization (full dataset to the left and filtered dataset to the right). The line corresponds to the green circles in Fig. 7

Another way to combine cell expansion and Tetris optimization is to apply Tetris optimization after every cell expansion. The blue line in Fig. 7 shows the effect of doing this. The blue line is almost as good as the green and black lines for the first 40 expansions. The green and black lines then become better for the full dataset, whereas for the filtered dataset the blue line is slightly better in some cases.

Fig. 7

Comparing the maximum number of subscribers as a function of the number of cell expansions for four different strategies (full dataset to the left and filtered dataset to the right). (Color figure online)

Finding the optimal combination and sequence of cell expansions and Tetris optimizations seems to be difficult, and one would probably need to do (close to) exhaustive testing to find the combination of m cell expansions and Tetris optimizations that yields the highest number of subscribers. Due to the large search space and relatively long execution times (see Sect. 6 for details), it is not possible to do (close to) exhaustive testing. It is, however, clear that adding a Tetris optimization as the last step in the optimization sequence will never decrease the number of subscribers. This means that it is a good idea to end the optimization sequence with a Tetris optimization (both the black and blue lines in Fig. 7 use a final Tetris optimization). Moreover, there is clearly no need to perform two consecutive Tetris optimizations without a cell expansion in between. For the case with 100 cell expansions we can thus have at most 100 Tetris optimizations (which is what we have with the blue line). We tested 100 random sequences of 100 cell expansions and 10 Tetris optimizations for the full dataset and got a maximum target value of 118,782, which is very close to the value for the black line for 100 cell expansions (see Fig. 6 and Table 2). The purple line in Fig. 8 is the maximum of all the lines in Fig. 7, and we believe that this line is close to the optimum. The gap between the purple and red lines in Fig. 8 is relatively constant, indicating that Tetris optimization provides a consistent performance gain regardless of the number of cell expansions.

Table 1 The number of subscribers in each segment for all time slots and cells for the small example

Table 2 The number of subscribers after 100 cell expansions for the four combinations evaluated

Fig. 8

Comparing the maximum number of subscribers as a function of the number of cell expansions with and without Tetris optimization (full dataset to the left and filtered dataset to the right). (Color figure online)

6 Discussion

In order to validate the basic assumptions about the spatiotemporal regularity of the user segments (see Assumption 1 in Sect. 3), we have evaluated the full dataset and a filtered version of the dataset. The main results and conclusions are very similar for both datasets, i.e., it would to a large extent be possible to predict the results in the full dataset by studying the filtered dataset. This shows that the basic assumption about spatiotemporal regularity is valid. We also investigated what would happen if the time interval length was changed from 5 min to 10 min. The results are shown in Fig. 9. The figure shows the same plot as in the left-hand side of Fig. 4, except that we have now merged the subscribers of two of the previous intervals into a single interval. For instance, the subscribers in cell X in the two intervals 08:00 to 08:05 and 08:05 to 08:10 are now merged into the interval 08:00 to 08:10 that contains the union of the subscribers in the two previous intervals. By comparing Figs. 4 and 9, we see that the results are similar. The main difference is that the curves in Fig. 9 are a bit lower, which is expected since Fig. 9 is based on the pessimistic assumption that all users in the interval (e.g., 08:00 to 08:10) are active during the entire interval. In Fig. 4, we know that some subscribers are active only during the first half of the interval (e.g., 08:00 to 08:05) and some subscribers are active only during the second half.

Fig. 9

The maximum number of subscribers as a function of the number of cell expansions for β = 3/2 for the full dataset and with 10-min time intervals. The green line shows the case with initial Tetris optimization. (Color figure online)

In this study we have assumed that all users generate the same revenue (Assumption 2 in Sect. 3). This may not be true since subscribers in some segments, such as Value aware, may generate more revenue than subscribers in other segments, such as Cost aware. Our methods can easily be adapted to handle such differences. We simply add a revenue coefficient r_j for each segment. Let r = (r₁,…,r_n)^T. Using the elementwise multiplication defined previously, we get the objective function

$${\text{Maximize}}\;\left( {{\mathbf{r}} \circ {\mathbf{s}}} \right)^{\text{T}} {\mathbf{x}}$$

(26)

In our small example (Sect. 4), if the subscribers in segment 2 generate 50% more revenue than those in segment 1 we get r₁ = 1 and r₂ = 1.5, i.e., r = (1, 1.5)^T. This means Maximize 60x₁+1.5 × 40x₂ = 60x₁+60x₂, thus resulting in an optimal x = (4, 4)^T, corresponding to a value of 480 for the objective function.

We also assume that all subscribers generate the same load in the cells they visit (Assumption 3 in Sect. 3). This may not be true, and it is possible to measure the average load that subscribers from different segments generate. Such information can easily be included in our methods by the addition of segment-specific coefficients in the restrictions. We simply introduce a load generation coefficient u_j for each segment. Let u = (u₁,…,u_n)^T. Using the elementwise multiplication defined previously, we get an updated set of restrictions

$$\left( {{\mathbf{u}} \circ {\mathbf{A}}} \right){\mathbf{x}} \le {\mathbf{Bc}}$$

(27)

In our small example, if the subscribers in segment 2 generate 20% more load than those in segment 1 we get the restrictions:

for t₁, cell 1: 40x₁ ≤ 200,

for t₁, cell 2: 20x₁+1.2 × 20x₂=20x₁+24x₂ ≤ 200,

for t₂, cell 1: 40x₁ ≤ 200,

for t₂, cell 2: 1.2 × 40x₂=48x₂ ≤ 200,

for t₃, cell 1: 25x₁+1.2 × 25x₂=25x₁+30x₂ ≤ 200,

for t₃, cell 2: 10x₁+1.2 × 15x₂=10x₁+18x₂ ≤ 200

This means that the revenue growth and the increase in load due to an increase in the number of subscribers from different segments can be estimated using the r and u vectors discussed above.

An approach similar to cell expansion can be used to reduce the number of radio cells, for instance, in order to save energy. In this case one can join a number of neighboring cells to one big cell. Before doing this one can use the same kind of approach as we have used, and add the number of subscribers in neighboring cells and investigate if the maximum capacity of the new large cell will be sufficient during all hours of the week. By using Tetris optimization, it is also possible to find the optimal subscriber mix for the reduced network. In the case of heterogeneous radio networks, where small cells are deployed within large macrocells (Wang et al. 2015), one can use an approach similar to ours to determine if some of the small cells can be turned off at night and during other non-peak hours. A small variation of Tetris optimization would make it possible to find the optimal subscriber mix for an energy-optimized network with different cell capacities during different hours of the week.

Cell expansion (or cell splitting) is an approach to incremental network expansion used by many operators. The method used in this paper makes it possible to predict the extent to which a certain number of cell expansions affects the maximum number of subscribers that we can accept without overloading the network. This makes it possible to compare the cost of expanding a certain number of cells with the revenue increase due to being able to handle more subscribers.

The x-axis in most of the figures in this paper represents the number of cell expansions. This can be seen as a linear cost scale (the number of subscribers on the y-axis can be seen as a linear revenue scale). However, as discussed in the previous section, some cells may be upgraded more than once, and the cost of splitting a cell two (or three) times is probably not two (or three) times higher than the cost of doing a single expansion. This should be taken into consideration in a cost-revenue analysis.

The number of subscribers in radio networks is growing, particularly if one considers the trend to an Internet of Things. Also, the bandwidth requirement of each user is growing, due to increased streaming of video and music, mobile gaming, etc. These trends increase the stress on the mobile networks and require cell splitting and other network densification mechanisms (Bhushan et al. 2014). As a consequence, optimization methods like those discussed here will become increasingly important.

Stochastic models based on state transition sequences have been used to model user mobility. However, the mobility patterns of subscribers in different user segments are not sufficiently well understood to create reliable stochastic models. This means that real mobility data, like the data we have used, are necessary to provide useful results, at least for Tetris optimization. Tetris optimization is a novel approach, and compared to cell expansion, it has the advantage that the number of subscribers can be increased without investing in the hardware infrastructure. In Sect. 5 we saw that Tetris optimization also makes it possible to maximize the benefits of a fixed budget for infrastructure expansion.

As discussed before, the LP problem was solved using an R program (2015) and the Gurobi solver (2016). It took approximately 20 CPU seconds to solve one instance of the optimization problem (i.e., generate one point in the lines in our figures) using an Intel i7-5600U CPU (2.6 GHz). We had only 8 GB RAM, which was insufficient. This resulted in some paging in the memory system, and because of this the wall clock time for solving one instance of the optimization problem was almost 2 min. This means that each unique line in Figs. 2, 3, 4, 5, 6, 7, 8 and 9 took approximately 3 h to generate.

We have made our R programs, including the s vector and the A matrix, available at http://cse.bth.se/~olra13/tetris/, ready to experiment with new strategies and combinations of Tetris optimization and selective cell expansions. Using these programs one can, for instance, evaluate different β (expansion factors) and how expansion factors other than β = 3/2 affect the graphs in Figs. 4, 5, 6, 7, 8 and 9. Another possibility is to evaluate how the targeting of a subset of the segments in a marketing campaign could affect the maximum number of users that the network can handle when we have a certain amount of unused capacity. For instance, when evaluating the potential of marketing campaigns targeted to segments 4 and 5 we add the restrictions x₁ = x₂ = x₃ = x₆ = 1 (i.e., we assume that all segments other than 4 and 5 are unaffected by the marketing campaigns). By using our R program, the effect of these ideas, and others, can be evaluated using our real-world dataset. Consequently, this addresses the well-known problem that there is a lack of common datasets in mobility data analysis (Naboulsi et al. 2015).

7 Conclusions

We have presented and evaluated two methods that make it possible to optimize utilization in a cellular radio network. The first is called Tetris optimization and makes it possible to optimize utilization through selective marketing to different subscriber segments without investing in the physical infrastructure. The second method is called selective cell expansion. Our approach to selective cell expansion makes it possible to make informed cost-revenue decisions when considering additional radio hardware investment in the cellular network. We have also evaluated how the two methods can be combined. The methods are based on subscriber mobility data, which is information that is readily available to telecom operators and other stakeholders.

We used real-world data from a region in Sweden and showed that Tetris optimization, based on the six user segments that a Nordic telecom operator currently uses, could increase the number of subscribers by up to 58% without upgrading the physical infrastructure. Moreover, by selectively expanding the capacity in less than 6% of the radio cells we were able to handle more than three times as many subscribers.

We have shown that the best way to combine Tetris optimization and cell expansion is to do Tetris optimization followed by cell expansion and then another Tetris optimization on the expanded infrastructure. With this approach we are able to handle more than four times as many subscribers when expanding less than 7% of the radio cells.

To validate some of the basic assumptions about spatiotemporal regularity, we have evaluated both the full dataset and a filtered version. The main results and conclusions are very similar for both, i.e., it would to a large extent be possible to predict the results in the full dataset by studying the filtered dataset. This shows that the basic assumption about spatiotemporal regularity is valid.

We have made our program, including the s vector and the A matrix, publicly available, making it possible to reproduce our results and evaluate new settings using our real-world data.

Appendix A: reducing the number of restrictions

The optimization problem that we consider has a large number of restrictions but a small number of variables (n). As a consequence, most of the restrictions are redundant in the sense that the target value will not improve if we remove the restriction. One obvious way of reducing the number is to remove any restriction r₁ for which there is another restriction r₂ such that the coefficient for variable y_j in r₁ is smaller than or equal to the coefficient for variable y_j in restriction r₂ for all $j\left( {1 \le j \le n} \right)$ (we have the same right-hand-side value c_l in all restrictions). It is however possible to remove even more restrictions.

Below we define an algorithm that reduces the number of restrictions. The main idea is to solve the relaxed problem a limited number of times (once for each iteration in the main loop of the algorithm). By systematically removing restrictions and solving the relaxed problem with fewer restrictions we can determine a small set of restrictions such that it suffices to consider this small set when searching for the optimal target value for the integer problem defined by (3)–(5). Unfortunately, this reduction of the number of restrictions needs to be repeated (i.e., it cannot be reused) if we change the optimization problem, e.g., when doing cell expansions.

Let $A$ be the set of all restrictions in the LP problem, and let T_u be the upper bound on the target function obtained by doing a full relaxation of the linear integer programming problem defined by (3)–(5). Let $R_{x} \left( {R_{x} \subseteq A} \right)$ be a set of restrictions, and let $T\left( {R_{x} } \right)$ be the target value when we consider only the restrictions in $R_{x}$, and relax the integer restriction, and subtract n from each c_l in $R_{x}$, and subtract n from the target function value. From Theorem 1 we know that $T\left( {R_{x} } \right)$ is a lower bound on the integer solution when we consider only the restrictions in $R_{x} \left( {R_{x} \subseteq A} \right)$. We now consider the set $R^{\prime }_{x} \left( {R^{\prime }_{x} \subseteq R_{x} } \right)$, where $R^{\prime }_{x}$ contains only the active restrictions in $R_{x}$, i.e., for each $R_{x}$ we get a $R^{\prime }_{x}$ and a $T\left( {R_{x} } \right)$. Consider a restriction $r\left( {r \in A} \right)$ and define $L\left( r \right) = \mathop {\hbox{min} }\nolimits_{{R_{x} \subseteq A}} \left( {T\left( {R_{x} } \right)|R^{\prime }_{x} \sum r} \right)$. If L(r) > T_u, then restriction r is active only when we consider subsets $R_{x}$ of A such that the lower bound on the integer solution $\left( {T\left( {R_{x} } \right)} \right)$ is above the upper bound on the integer solution (T_u). From Lemma 1 below, we see that all such restrictions r can be removed without affecting the target value of the solution of the integer problem defined by (3)–(5).

Let S be the set of all sets of restrictions $R_{x} \left( {R_{x} \subseteq A} \right)$ such that $T\left( {R_{x} } \right) \le T_{u}$, and let $S^{\prime }$ be the set of the corresponding sets of restrictions $R_{x} ^{\prime }$ (as mentioned above, $R\prime_{x}$ is the set of active restrictions in $R_{x}$). We now define the set of restrictions $S^{\prime \prime }$ as

$$S^{\prime \prime } = \mathop {\bigcup }\limits_{{r \in R_{x} ^{\prime } and R_{x} ^{\prime } \in S^{\prime }}} r$$

Based on the discussion above, it is clear that $S^{\prime \prime }$ contains all the restrictions that could affect the target value for the integer solution, i.e., all restrictions that are not in $S^{\prime \prime }$ can be removed without affecting the value of the target value of the integer solution.

Lemma 1

For each restriction r that affects the target value of the integer problem defined by (3)–(5) there is a set of restrictions$R_{x} \left( {R_{x} \subseteq A} \right)$, such that$r \in R_{x} \prime$and$T\left( {R_{x} } \right) \le T_{u}$.

Proof

Let $T_{0}$ be the target value of the integer problem defined by (3)–(5), and let $R_{0}$ be a set of restrictions such that the removal of any restriction in $R_{0}$ increases $T_{0}$. From the definition of $R_{0}$, it is clear that if restriction r affects the target value of the integer problem, then $r \in R_{o}$. From Theorem 1 we see that $T\left( {R_{0} } \right) \le T_{0} \left( {T\left( {R_{x} } \right)} \right)$ is defined above). Since $T_{0} \le T_{u}$, it follows that $T\left( {R_{0} } \right) \le T_{u}$, which proves the lemma.$\square$

Remark

Depending on the restrictions, there could be more than one set $R_{0}$, but each $R_{0}$ results in the same target value $T_{0}$. If there are two sets $R_{0}^{'}$ and $R_{0}^{{\prime \prime }}$, our algorithm will find all restrictions that belong to either one of these sets, i.e., in that case $R_{0} = R_{0}^{'} \cup R_{0}^{\prime \prime }$. Obviously, the target value when using the restrictions in the set $R_{0} = R_{0}^{'} \cup R_{0}^{\prime \prime }$ is still $T_{0}$. However, if $R_{0}^{'} \ne R_{0}^{\prime \prime }$, it is possible to remove some restriction r from $R_{0} = R_{0}^{'} \cup R_{0}^{\prime \prime }$ without increasing the target value $T_{0}$, i.e., in this case we have included more restrictions than necessary in our set $S^{\prime \prime }$. This does not affect the correctness of Lemma 1.

The following algorithm finds the restrictions in $S^{\prime \prime }$:

Theorem 2

After the algorithm above, $S^{\prime \prime }$contains all the restrictions that we need to consider in order to obtain an integer solution to the original optimization problem.

Proof

Step 8 in the algorithm guarantees that if $T\left( {R_{x} } \right) \le T_{u}$, then $R'_{x} \subseteq S''$. Lemma 1 tells us that for each restriction r that affects the target value of the integer problem defined by (3)–(5) there is a set of restrictions $R_{x} \left( {R_{x} \subseteq A} \right)$ such that $r \in R_{x}^{'}$ and $T\left( {R_{x} } \right) \le T_{u}$.$\square$

Example

Consider the following problem with two parameters and four restrictions:

Maximize y₁ + y₂

subject to

• 1. $\left\lceil {0.205y_{1} } \right\rceil + \left\lceil {0.205y_{2} } \right\rceil \le 10$

• 2. $\left\lceil {0.42y_{1} } \right\rceil \le 10$

• 3. $\left\lceil {0.42y_{2} } \right\rceil \le 10$

• 4. $\left\lceil {0.16y_{1} } \right\rceil + \left\lceil {0.16y_{2} } \right\rceil \le 10$

$$y_{1} , y_{2} \in {\mathbb{Z}},\text{ }y_{1} , y_{2} \ge 0$$

The optimal solution for the integer problem is y₁ = y₂ = 23 (i.e., $T_{0} = y_{1} + y_{2} = 46$) and the optimal solution for the relaxed problem is y₁ = y₂ = 23.81 (i.e., $T_{u} = y_{1} + y_{2} = 47.62$). After removing n (n = 2) from all c_l (c_l = 10) and solving the corresponding relaxed problem we get the target value T = 38.10, which is less than T_u + n = 47.62 + 2 = 49.62. The active restrictions are restrictions 2 and 3 above. If we remove restriction 2 and solve the LP problem, we get a target value T = 39.02 and the active restrictions are restrictions 1 and 3. After a small number of iterations, we reach a set $S^{\prime \prime }$ containing restrictions 1, 2, and 3. For restriction 4 to be active we need to remove restriction 1 and one of restrictions 2 and 3. We then get a target value T = 50, which is larger than 49.62. This means that restriction 4 will not be a part of set $S^{\prime \prime }$. Theorem 2 now tells us that we need to consider only restrictions 1, 2, and 3 to obtain an optimal solution to the integer problem.

Remark

For the LP problem considered in this paper, we were able to reduce the number of restrictions that we need to consider by more than a factor of 10,000. In Step 7 of the algorithm we go through the power set of $\left( {S^{\prime\prime} - R_{x} } \right)$; this is manageable since $S^{\prime \prime }$ is relatively small. The execution time was approximately 1 h using the hardware described in Sect. 6.