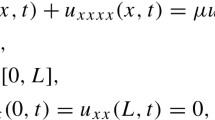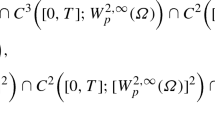Skip to main content
SpringerLink
Log in

High-order half-step compact numerical approximation for fourth-order parabolic PDEs

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

The aim of this study is to develop compact difference method to approximate parabolic PDEs of fourth order equipped with Dirichlet and Neumann boundary conditions involving half-step points. The proposed method converges quaternary and quadratically in space and time, respectively. The imbedding technique has been applied to approximate derivative terms of lower order by means of the governing differential equation to deduce the high-order method. The primary utility of this new discretization is that it can be straightaway applied to problems with singularities without necessitating fictitious nodes or special approach which has consequently lowered computational complicacy. We have examined linear stability of the proposed three-level implicit difference scheme using matrix stability analysis. In addition, we also obtained the solution of the first-order spatial derivative which is of significance in several physical problems. The efficacy of the proposed approximation is confirmed through numerical tests performed on a collection of physically relevant problems comprising the Euler Bernoulli beam equation and the highly nonlinear good Boussinesq equation. Numerical experiments evidently exhibit that the method provides more accurate results in contrast with the existing numerical techniques. The present method is able to simulate well the complex and intriguing long time dynamics of the good Boussinesq equation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Data availibility

Because no datasets were collected or analyzed during the present investigation, data sharing is not applicable to this publication.

References

  1. Mohebbi, A., Asgari, Z.: Efficient numerical algorithms for the solution of “good” Boussinesq equation in water wave propagation. Comput. Phys. Comm. 182, 2464–2470 (2011)

  2. Almatrafi, M.B., Alharbi, A.R.: Tunç, Cemil: Constructions of the soliton solutions to the good Boussinesq equation. Adv. Difference Equ. Paper No. 629 (2020)

  3. Boussinesq, M.J.: Theory of waves and vortices propagating along a horizontal rectangular channel, communicating to the liquid in the channel generally similar velocities of the bottom surface. J. Math. Pures Appl. 17, 55–108 (1872)

    MathSciNet  Google Scholar 

  4. Bratsos, A.G.: The solution of the Boussinesq equation using the method of lines. Comput. Methods Appl. Mech. Eng. 157, 33–44 (1998)

    Article  ADS  MathSciNet  Google Scholar 

  5. Bratsos, A.G.: A second order numerical scheme for the solution of the one-dimensional Boussinesq equation. Numer. Algor. 46, 45–58 (1872)

    Article  ADS  MathSciNet  Google Scholar 

  6. Brugnano, L., Gurioli, G., Zhang, C.: Spectrally accurate energy-preserving methods for the numerical solution of the “good’’ Boussinesq equation. Numer. Methods Partial. Differ. Equ. 35, 1343–1362 (2019)

    Article  MathSciNet  Google Scholar 

  7. Cai, J., Wang, Y.: Local structure-preserving algorithms for the “good’’ Boussinesq equation. J. Comput. Phys. 239, 72–89 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  8. Chawla, M.M., Shivakumar, P.N.: An efficient finite difference method for two-point boundary value problems. Neural Parallel Sci. Comput. 4, 387–395 (1996)

    MathSciNet  Google Scholar 

  9. Chen, M., Kong, L., Hong, Y.: Efficient structure-preserving schemes for good Boussinesq equation. Math. Methods Appl. Sci. 41, 1743–1752 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  10. Dehghan, M., Salehi, R.: A meshless based numerical technique for traveling solitary wave solution of Boussinesq equation. Appl. Math. Model. 36, 1939–1956 (2012)

    Article  MathSciNet  Google Scholar 

  11. El-Gamel, M.: A note on solving the fourth-order parabolic equation by the sinc-Galerkin method. Calcolo 52, 327–342 (2015)

    Article  MathSciNet  Google Scholar 

  12. Gorman, D.G.: Free vibrations analysis of beams and shafts. Wiley, New York (1975)

    Google Scholar 

  13. Hageman, L.A., Young, D.M.: Applied iterative methods. Dover Publication, New York (2004)

    Google Scholar 

  14. Ismail, M.S., Mosally, F.: A fourth order finite difference method for the good Boussinesq equation. Abstr. Appl. Anal. Art. ID 323260, 10 (2014)

    Google Scholar 

  15. Jiang, C., Sun, J., He, X., Zhou, L.: High order energy-preserving method of the “good’’ Boussinesq equation. Numer. Math. Theory Methods Appl. 9, 111–122 (2016)

    Article  MathSciNet  Google Scholar 

  16. Kaur, D., Mohanty, R.K.: Highly accurate compact difference scheme for fourth order parabolic equation with Dirichlet and Neumann boundary conditions: Application to good Boussinesq equation. Appl. Math. Comput. 378(125202) (2020)

  17. Kelly, C.Y.: Iterative methods for linear and non-linear equations. SIAM Publications, Philadelphia (1995)

    Book  Google Scholar 

  18. Manoranjan, V.S., Mitchell, A.R., Morris, JLl.: Numerical solutions of the good Boussinesq equation. SIAM J. Sci. Statist. Comput. 5, 946–957 (1984)

    Article  MathSciNet  Google Scholar 

  19. Maruno, K., Biondini, G.: Resonance and web structure in discrete soliton systems: the two-dimensional Toda lattice and its fully discrete and ultradiscrete analogues. J. Phys. A: Math. Gen. 37, 11819–11839 (2004)

    Article  ADS  Google Scholar 

  20. Meirovitch, L.: Principles and techniques of vibrations. Prentice Hall, New Jersey (1997)

    Google Scholar 

  21. Mohammadi, R.: Sextic B-spline collocation method for solving Euler-Bernoulli beam models. Appl. Math. Comput. 241, 151–166 (2014)

    MathSciNet  Google Scholar 

  22. Mohanty, R.K., Kaur, D.: Unconditionally stable high accuracy compact difference schemes for multi-space dimensional vibration problems with simply supported boundary conditions Appl. Math. Model. 55, 281–298 (2018)

    Article  MathSciNet  Google Scholar 

  23. Ostermann, A., Su, C.: Two exponential-type integrators for the “good’’ Boussinesq equation. Numer. Math. 143, 683–712 (2019)

    Article  MathSciNet  Google Scholar 

  24. Saad, Y.: Iterative methods for sparse linear systems. SIAM Publisher (2003)

  25. Smith, R.C., Bowers, K.L., Lund, J.: A fully sinc-Galerkin method for Euler-Bernoulli beam models. Numer. Methods Part. Differ. Equ. 8, 171–202 (1992)

    Article  MathSciNet  Google Scholar 

  26. Soh, C.W.: Euler-Bernoulli beams from a symmetry standpoint-characterization of equivalent equations. J. Math. Anal. Appl. 45, 387–395 (2008)

    MathSciNet  Google Scholar 

  27. Su, C., Yao, W.: A Deuflhard-type exponential integrator Fourier pseudo-spectral method for the “good” Boussinesq equation. J. Sci. Comput. Paper No. 4, 83, 19 (2020)

  28. Ucar, Y., Esen, A., Karaagac, B.: Numerical solutions of Boussinesq equation using Galerkin finite element method. Numer. Methods Part. Differ. Equ. 37, 1612–1630 (2021)

    Article  MathSciNet  Google Scholar 

  29. Uddin, M., Haq, S., Ishaq, M.: RBF-pseudospectral method for the numerical solution of good Boussinesq equation. Appl. Math. Sci. (Ruse) 6, 2403–2410 (2012)

    MathSciNet  Google Scholar 

  30. Yan, J., Zhang, Z.: New energy-preserving schemes using Hamiltonian boundary value and Fourier pseudospectral methods for the numerical solution of the “good’’ Boussinesq equation Comput. Phys. Commun. 201, 33–42 (2016)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  31. Zhang, C., Huang, J., Wang, C., Yue, X.: On the operator splitting and integral equation preconditioned deferred correction methods for the “good’’ Boussinesq equation. J. Sci. Comput. 75, 687–712 (2018)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

We are thankful to Science and Engineering Research Board (SERB) (Sanction Order No.: CRG/2018/004608) for providing support during this research work.

Author information

Authors and Affiliations

  1. Department of Mathematics, Mata Sundri College for Women, University of Delhi, Delhi, 110002, India

    Deepti Kaur

  2. Department of Applied Mathematics, Faculty of Mathematics and Computer Science, South Asian University, Rajpur Road, Maidan Garhi, New Delhi, 110068, India

    R. K. Mohanty

Authors
  1. Deepti Kaur
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. K. Mohanty
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

In this work, all authors contributed equally.

Corresponding author

Correspondence to R. K. Mohanty.

Ethics declarations

Ethical approval

There are no studies involving human participants or animals done by any of the authors in this article.

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kaur, D., Mohanty, R.K. High-order half-step compact numerical approximation for fourth-order parabolic PDEs. Numer Algor 95, 1127–1153 (2024). https://doi.org/10.1007/s11075-023-01602-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-023-01602-0

Keywords

Mathematics Subject Classification (2010)

Search

Navigation