Skip to main content
SpringerLink
Log in

Boundary value problems initial condition identification by a wavelet-based Galerkin method

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

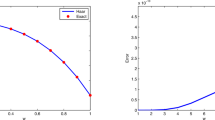
In this study, we introduce a numerical method to reconstruct, from posterior measurements of the solution, the initial condition in the one-dimensional heat conduction problem. The method uses a wavelet-based Galerkin method for the spatial discretization and spectral decomposition of the basis stiffness matrix to get the numerical solution without time discretization as in classical approaches. In fact, according to the proposed method, setting an error bound and properly selecting the eigenvalues of the discretization system, we are able to reconstruct the initial conditions without exceeding the required error. The applicability and computational efficiency of the methods are investigated by solving some numerical examples with toy solutions and the experimental results confirm its accuracy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Beylkin, G.: On the representation of operator in bases of compactly supported wavelets. SIAM J. Numer. Anal. 6, 1716–1740 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  2. Beylkin, G., Keiser, J. M., Vozovoi, L.: A new class of time discretization schemes for the solution of nonlinear PDEs. J. Comput. Phys. 147, 362–387 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  3. Choulli, M.: Une introduction aux problèmes inverses elliptiques et paraboliques, Mathématiques & Applications, vol. 65. Springer, Berlin (2009)

    Book  MATH  Google Scholar 

  4. Cohen, A.: Numerical Analysis of Wavelet Methods, Studies in Mathematics and Its Applications. Elsevier, Amsterdam (2003)

    Google Scholar 

  5. Cohen, A., Daubechies, I., Feauveau, J.-C.: Biorthogonal bases of compactly supported wavelets. Comm. Pure. Appli. Maths. 45, 485–560 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  6. Daubechies, I.: Ten Lectures on Wavelets, Book. SIAM, Pennsylvania (1992)

    Book  MATH  Google Scholar 

  7. DeVore, R., Zuazua, E.: Recovery of an initial temperature from discrete sampling. Math. Models. Meth. Appl. Sci. 12, 2487–2501 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  8. Deslauriers, G., Dubuc, S.: Symmetric iterative interpolation processes. Constr. Approx. 5, 49–68 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  9. Dubuc, S.: Interpolation through an iterative scheme. J. Math. Anal. Appl. 114, 185–204 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  10. Hochbruck, M., Ostermann, A.: Exponential integrators. Acta Numer 19, 209–286 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  11. Imperiale, S., Moireau, P., Tonnoir, A.: Analysis of an observer strategy for initial state reconstruction of wave-like systems in unbounded domains. ESAIM COCV 26, 45 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  12. Kadri Harouna, S., Perrier, V.: Homogeneous Dirichlet wavelets on the interval diagonalizing the derivative operator, and application to free-slip divergence-free wavelets, J. Math. Anal. Appli. 505, 125479 (2022) 

  13. Komornik, V., Loreti, P.: Fourier Series in Control Theory. Springer Science & Business Medi, Berlin (2005)

    Book  MATH  Google Scholar 

  14. Krogstad, S.: Generalized integrating factor methods for stiff PDEs. J. Comp. Phys. 203, 72–88 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  15. Larsson, S., Thomee, V.: Partial Differential Equations with Numerical Methods. Springer Science & Business Media, Berlin (2003)

    MATH  Google Scholar 

  16. Lattès, R., Lions, J. -L.: Méthode De Quasi-Réversibilité et Applications. Dunod, Paris (1967)

    MATH  Google Scholar 

  17. Mallat, S.: A Wavelet Tour of Signal Processing: The Sparse Way. Academic Press, Cambridge (2008)

    MATH  Google Scholar 

  18. Monasse, P., Perrier, V.: Orthogonal wavelet bases adapted for partial differential equations with boundary conditions. SIAM J. Math. Anal. 29, 1040–1065 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  19. Payne, L. E.: Improperly Posed Problems in Partial Differential Equations. SIAM, Philadelphia (2017)

    MATH  Google Scholar 

  20. Phung, K. D., Wang, G., Xu, Y.: Impulse output rapid stabilization for heat equations. J. Diff. Equ. 263, 5012–5041 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  21. Qiu, C., Feng, X.: A wavelet method for solving backward heat conduction problems. Elect. J. Diff. Equ. 219, 1–9 (2017)

    MathSciNet  MATH  Google Scholar 

  22. Seidman, T. I.: Optimal filtering for the backward heat equation. SIAM J. Num. Anal. 33, 162–170 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  23. Shukla, A., Mehra, M.: Spectral graph wavelet regularization and adaptive wavelet for the backward heat conduction problem. Inverse Problems Sci. Eng. 29, 457–488 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  24. Strang, G.: Introduction to Linear Algebra. Wellesley-Cambridge Press, Wellesley (1993)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. LR Analysis and Control of PDEs, LR22ES03, Department of Mathematics Faculty of Sciences of Monastir, University of Monastir, 5019, Monastir, Tunisia

    Kadri Harouna Souleymane

  2. Laboratoire Mathématiques, Image et Applications (MIA), Université de La Rochelle, Avenue Michel Crépeau, 17042, La Rochelle, France

    Kaïs Ammari

Authors
  1. Kadri Harouna Souleymane
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kaïs Ammari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kadri Harouna Souleymane.

Ethics declarations

The authors have no conicts of interest to declare and there is no financial interest to report. We certify that the submission is original work and is not under review at any other publication.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

The data sets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request. The author can also provide the numerical codes for the work evaluation if necessary.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Souleymane, K.H., Ammari, K. Boundary value problems initial condition identification by a wavelet-based Galerkin method. Numer Algor 93, 397–414 (2023). https://doi.org/10.1007/s11075-022-01421-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-022-01421-9

Keywords

Search

Navigation