Skip to main content
SpringerLink
Log in

Unconditional error estimates of linearized BDF2-Galerkin FEMs for nonlinear coupled Schrödinger-Helmholtz equations

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

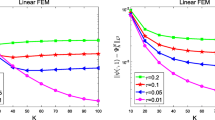
In this paper, we present two linearized BDF2 Galerkin FEMs for the nonlinear and coupled Schrödinger-Helmholtz equations. Different from the standard linearized second-order Crank-Nicolson methodology, we employ backward differential concept to obtain second-order temporal accuracy at the time step tn (instead of the time instant tn+ 1/2) and apply semi-implicit or explicit treatment of nonlinear terms to formulate the decoupled schemes. We prove optimal error estimates for r-order FEM without any grid-ratio condition through a so-called temporal-spatial error splitting technique, and some sharp estimations to cope with the nonlinear terms. Finally, we provide two numerical experiments to illustrate the theoretical analysis and the efficiency of the proposed methods. Here, h is the spatial subdivision parameter, and τ is the time step.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Bohun, S., Illner, R., Lange, H., Zweifel, P.F.: Error estimates for Galerkin approximations to the periodic Schrödinger-Poisson system, ZAMMZ. Angew. Math. Mech 76(1), 7–13 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  2. Harrison, R., Moroz, I., Tod, K.P.: A numerical study of the Schrödinger-Newton equations. Nonlinearity 16(1), 101–122 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  3. Leo, M.D., Rial, D.: Well posedness and smoothing effect of Schrödinger-Poisson equation. J. Math. Phys 48, 093509 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  4. Lubich, C.: On splitting methods for Schrödinger-Poisson and cubic nonlinear Schrödinger equations. Math. Comput 77, 2141–2153 (2008)

    Article  MATH  Google Scholar 

  5. Masaki, S.: Energy solution to a Schrödinger-Poisson system in the two-dimensional whole space. SIAM J. Math. Anal 43(6), 2719–2731 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  6. Antoine, X., Besse, C., Klein, P.: Absorbing boundary conditions for general nonlinear Schrödinger equations. SIAM J. Sci. Comput 33(2), 1008–1033 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  7. Pelinovsky, D.E., Afanasjev, V.V., Kivshar, Y.S.: Nonlinear theory of oscillating, decaying, and collapsing solitons in the generalized nonlinear Schrödinger equation. Phys. Rev. E 53(2), 1940–1953 (1996)

    Article  Google Scholar 

  8. Bao, W., Mauser, N.J., Stimming, H.P.: Effective one particle quantum dynamics of electrons: a numerical study of the Schrödinger-Poisson-Xα model. Commun. Math. Sci 1(4), 809–828 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  9. Zhang, Y., Dong, X.: On the computation of ground state and dynamics of Schrödinger-Poisson-Slater system. J. Comput. Phys 230, 2660–2676 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  10. Mauser, N.J.: The Schrödinger-Poisson-Xα equation. Appl. Math. Lett 14, 759–763 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  11. Stimming, H.P.: The IVP for the Schrödinger-Poisson-Xα equation in one dimension. Math. Models Methods Appl. Sci 15(8), 1169–1180 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  12. Cao, Y., Musslimani, Z.H., Titi, E.S.: Nonlinear Schrödinger-Helmholtz equation as numercal regularization of the nonlinear Schrödinger equation. Nonlinearity 21, 879–898 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  13. Bao, W., Cai, Y.: Uniform error estimates of finite difference methods for the nonlinear Schrödinger equation with wave operator. SIAM J. Numer. Anal 50(2), 492–521 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  14. Bratsos, A.G.: A modified numerical scheme for the cubic Schrödinger equation. Numer. Methods Partial Differ. Equ 27(3), 608–620 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  15. Liao, H., Sun, Z., Shi, H.: Error estimate of fourth-order compact scheme for linear Schrödinger equations. SIAM J. Numer Anal 47(6), 4381–4401 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  16. Zhang, L.: Convergence of a conservative difference schemes for a class of Klein-Gordon-Schrödinger equations in one space dimension. Appl. Math. Comput 163(1), 343–355 (2005)

    MathSciNet  MATH  Google Scholar 

  17. Wang, T., Jiang, Y.: Point-wise errors of two conservative difference schemes for the Klein-Gordon-Schrödinger equation. Commun. Nonlinear Sci. Numer. Simulat 17(12), 4565–4575 (2012)

    Article  MATH  Google Scholar 

  18. Wang, T., Zhao, X., Jiang, J.: Unconditional and optimal H2-error estimates of two linear and conservative finite difference schemes for the Klein-Gordon-Schrödinger equation in high dimensions. Adv. Comput. Math 44(5), 477–503 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  19. Xiang, X.: Spectral method for solving the system of equations of Schrödinger-Klein-Gordon field. J. Comput. Appl. Math 21 (2), 161–171 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  20. Kong, L., Wang, L., Jiang, S., Duan, Y.: Multisymplectic Fourier pseudo-spectral integrators for Klein-Gordon-Schrödinger equations. Sci. China Math 56, 915–932 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  21. Hong, Q., Wang, Y., Wang, J.: Optimal error estimate of a linear Fourier pseudo-spectral scheme for two dimensional Klein-Gordon-Schrödinger equations. J. Math. Anal. Appl 468(2), 817–838 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  22. Fu, Y., Cai, W., Wang, Y.: Structure-preserving algorithms for multi-dimensional fractional Klein-Gordon-Schrödinger equation. Appl. Numer. Math. 156, 77–93 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  23. Wang, J.: A New Error Analysis of Crank-Nicolson Galerkin FEMs for a Generalized Nonlinear Schrödinger Equation. J. Sci. Comput 60, 390–407 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  24. Shi, D., Wang, P., Zhao, Y.: Superconvergence analysis of anisotropic linear triangular finite element for nonlinear Schrödinger equation. Appl. Math. Lett 38, 129–134 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  25. Shi, D., Wang, J.: Unconditional Superconvergence analysis of a Crank-Nicolson Galerkin FEM for nonlinear Schrödinger equation. J. Sci. Comput 72 (3), 1093–1118 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  26. Zhang, H., Wang, J.: Superconvergence analysis of Crank-Nicolson Galerkin FEMs for a generalized nonlinear Schrödinger equation. Numer. Methods Partial Differ. Equ 34(2), 799–820 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  27. Zhang, H., Shi, D., Li, Q.: Nonconforming finite element method for a generalized nonlinear Schrödinger equation. Appl. Math. Comput 377, 125141 (2020)

    MathSciNet  MATH  Google Scholar 

  28. Cai, W., He, D., Pan, K.: A linearized energy-conservative finite element method for the nonlinear Schrödinger equation with wave operator. Appl. Numer. Math 140, 183–198 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  29. Li, M., Shi, D., Wang, J.: Unconditional superconvergence analysis of the conservative linearized Galerkin FEMs for nonlinear Klein-Gordon-Schrödinger equation. Appl. Numer. Math 142, 47–63 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  30. Yang, Y., Jiang, Y.: Unconditional optimal error estimates of linearized backward Euler Galerkin FEMs for nonlinear Schrödinger-Helmholtz equations. Numer. Algor 86(4), 1495–1522 (2021)

    Article  MATH  Google Scholar 

  31. Wang, J.: Unconditional stability and convergence of Crank-Nicolson Galerkin FEMs for a nonlinear Schrödinger-Helmholtz system. Numer. Math 139, 479–503 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  32. Li, D., Wang, J.: Unconditionally optimal error analysis of Crank-Nicolson Galerkin FEMs for a strongly nonlinear Parabolic system. J. Sci. Comput 72, 892–915 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  33. Sun, W., Wang, J.: Optimal error analysis of Crank-Nicolson schemes for a coupled nonlinear Schrödinger system in 3D. J. Comput. Appl. Math 317, 685–699 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  34. Shi, D., Li, C.: Superconvergence analysis of two-grid methods for bacteria equations. Numer. Algor 86(1), 123–152 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  35. Li, B., Gao, H., Sun, W.: Unconditionally optimal error estimates of a Crank-Nicolson Galerkin method for the nonlinear Thermistor equations. SIAM J. Numer. Anal 52(2), 933–954 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  36. Amanda, E., Wang, C., Steven, M.: Stability and convergence of a second order mixed finite element method for the Cahn-Hilliard Equation. IMA J. Numer. Anal 36, 1867–1897 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  37. Shi, D., Yan, F., Wang, J.: Unconditional superconvergence analysis of a new mixed finite element method for nonlinear Sobolev equation. Appl. Math. Comput 274, 182–194 (2016)

    MathSciNet  MATH  Google Scholar 

  38. Gear, C.: Numerical Initial Value Problems in Ordinary Differential Equations. Prentice-Hall, Englewood Cliffs (1971)

    MATH  Google Scholar 

  39. Lambert, J.: Numerical Methods in Ordinary Differential Systems: the Initial Value Problems. Wiley, Chichester (1991)

    MATH  Google Scholar 

  40. Gao, H.: Unconditional optimal error estimates of BDF-Galerkin FEMs for nonlinear thermistor equations. J. Sci. Comput 66, 504–527 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  41. Li, B., Sun, W.: Error analysis of linearized semi-implicit Galerkin finite element methods for nonlinear parabolic equations. Int. J. Numer. Anal. Model 10, 622–633 (2013)

    MathSciNet  MATH  Google Scholar 

  42. Li, B., Sun, W.: Unconditional convergence and optimal error estimates of a Galerkin-mixed FEM for incompressible miscible flow in porous media. SIAM J. Numer. Anal 51, 1959–1977 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  43. Thomée, V.: Galerkin Finite Element Methods for Parabolic Problems. Springer Series in Computational Mathematics, Sweden (2000)

    MATH  Google Scholar 

  44. Lin, Q., Lin, J.: Finite element methods: Accuracy and improvement. Science Press, Beijing (2006)

    Google Scholar 

  45. Evans, L.C.: Partial Differential Equations, 2nd edn. AMS, Providence (2010)

    MATH  Google Scholar 

  46. Liao, H., Song, X., Tang, T., et al.: Analysis of the second order BDF scheme with variable steps for the molecular beam epitaxial model without slope selection. Sci. China Math 64, 887–902 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  47. Liao, H., Ji, B., Zhang, L.: An adaptive BDF2 implicit time-stepping method for the phase field crystal model. IMA J. Numer. Anal. in review arXiv:2008.00212v1 (2020)

  48. Liao, H., Tang, T., Zhou, T.: On energy stable, maximum-principle preserving, second-order BDF scheme with variable steps for the Allen–Cahn equation. SIAM J. Numer. Anal 58(4), 2294–2314 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  49. Zhou, G., Saito, N.: Finite volume methods for a Keller-Segel system: Discrete energy, error estimates and numerical blow-up analysis. Numer. Math 135, 265–311 (2017)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

This work was supported by the National Natural Science Foundation of China (No. 12071443); the Key Scientific Research Projects of Henan Colleges and Universities (No. 20B110013).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Zhengzhou University, Zhengzhou, 450001, China

    Dongyang Shi & Houchao Zhang

Authors
  1. Dongyang Shi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Houchao Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Houchao Zhang.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Data availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shi, D., Zhang, H. Unconditional error estimates of linearized BDF2-Galerkin FEMs for nonlinear coupled Schrödinger-Helmholtz equations. Numer Algor 92, 1679–1705 (2023). https://doi.org/10.1007/s11075-022-01360-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-022-01360-5

Keywords

Mathematics Subject Classification (2010)

Search

Navigation