Two-grid finite element method for the dual-permeability-Stokes fluid flow model

Abstract

In this paper, two-grid finite element method for the steady dual-permeability-Stokes fluid flow model is proposed and analyzed. Dual-permeability-Stokes interface system has vast applications in many areas such as hydrocarbon recovery process, especially in hydraulically fractured tight/shale oil/gas reservoirs. Two-grid method is popular and convenient to solve a large multiphysics interface system by decoupling the coupled problem into several subproblems. Herein, the two-grid approach is used to reduce the coding task substantially, which provides computational flexibility without losing the approximate accuracy. Firstly, we solve a global problem through standard P_k − P_k− 1 − P_k − P_k finite elements on the coarse grid. After that, a coarse grid solution is applied for the decoupling between the interface terms and the mass exchange terms to solve three independent subproblems on the fine grid. The three independent parallel subproblems are the Stokes equations, the microfracture equations, and the matrix equations, respectively. Four numerical tests are presented to validate the numerical methods and illustrate the features of the dual-permeability-Stokes model.

1 Introduction

Over the last few years, Stokes-Darcy and related multiphysics problems have notable importance due to their practical applications such as groundwater problems in karst aquifers [1, 2], industrial filtration [3], petroleum extraction [4], the interaction between surface and subsurface flows [5,6,7,8,9], blood flow in the artery and vein [10,11,12], and fluid-structure interactions [13, 14]. For these practical applications, researchers usually used the traditional Stokes-Darcy model extensively over the past few decades.

On the other hand, the hydraulically fractured reservoir contains more than half of the world remaining petroleum resources, and the extraction of the hydrocarbon occurs from fractured formations, including naturally fractured reservoirs (NFRs), coal bed methane (CBM), and tight fractured gas reservoirs [15,16,17,18]. Nowadays, the universal requirements of the energy demands are met by the petroleum industry which is extracted from the NFRs. But it is believed that the economic hydrocarbon extraction from the NFRs depends on the reservoir’s intrinsic properties, especially fracture permeability [15, 19, 20]. Regarding the fact that naturally fractured reservoirs (NFRs) are intrinsically heterogeneous at all scales, a large number of reservoir contains two different scale flow mechanisms which cannot be modeled explicitly, nor homogenized in the reservoir simulation model [21]. For example, in the shale/tight oil/gas reservoir, the matrix permeability is 10⁵ to 10⁷ times smaller than the microfracture permeability while the matrix porosity is usually 10² to 10³ times larger than the microfracture porosity [22,23,24,25,26]. Hence, a dual-permeability/porosity model must incorporate a transfer function between matrix and fracture in order to predict the optimal recovery mechanism from the fractured reservoir [21]. In the dual-porosity conceptualization, the tight matrix is considered with the large storativity of fluid, while the networks of fractures are assumed with high fluid conductivity [27]. As a result, the matrix system and the microfracture region can be adopted as two overlapping but interacting media with different hydraulic and transport properties [23, 28].

To this end, the first dual-porosity/dual-permeability fluid flow model (DPM) was proposed by Barenblatt et al. in 1960 by considering dual-continua for naturally fractured reservoirs [29]. The dual-continuum approach provides a mathematical framework for the fluid flow and mass exchange between matrix block and microfracture region. This concept was originally applied to the reservoir engineering by Warren and Root in 1963 [30] to characterize and simulate the flow pattern in the realistic naturally fractured reservoir. Moreover, they introduced a shape factor in the mass transfer function, which is one of the key parameter in the pressure transient analysis [30,31,32]. Based on the model proposed by Warren and Root [30], the dual-permeability/porosity fluid flow model concept has been considered to simulate flows through naturally fractured reservoirs because of the specificity of those media: fluids are mainly stored in the matrix region (primary pores) and flow to the wellbore through the fracture system (secondary pores) [33,34,35,36,37,38,39,40]. The matrix block, considered as a stagnant medium with high porosity and lower permeability, acts as the primary storage of fluid. The fracture region consists of lower porosity with higher permeability and feeds the wellbore or conduits while it receives the fluid from the matrix region only [23, 24, 34, 41, 42]. Besides, the dual-porosity model can be improved by considering integrated discrete fracture networks [43].

It is worthwhile noting that the Stokes-Darcy fluid flow model cannot describe the heterogeneous intrinsic properties in the groundwater flow region since it deals with single permeability in the porous medium. To model the multiple porosity, various permeability and different intrinsic properties of the naturally fractured reservoir, dual-porosity and dual-permeability fluid flow model is the appropriate choice. Hence, the dual-porosity-Stokes model is more effective and appropriate for realistic reservoir engineering, which was recently introduced by Hou et al. in [23]. Later, Shan et al. studied the dual-porosity-Stokes system by using partitioned time-stepping method for Beavers-Joseph interface condition [26]. On the other hand, Mahbub et al. investigate the dual-porosity-Stokes fluid flow model by using stabilized mixed finite element method in [28]. The dual-permeability-Stokes model can be used to study the flow and transport processes in underground natural-resources recovery, especially petroleum extraction, tight/shale oil/gas recovery, carbon sequestration, geothermal system, waste storage, contaminant remediation and so on [22,23,24, 26, 28, 44,45,46,47,48,49,50].

In practice, there are two main approaches used for solving the multiphysics problems. The first approach is to solve a coupled problem directly, and the second one is to decouple the whole problem into several subproblems and then apply an appropriate technique to solve local problems individually. Furthermore, to solve the coupled problem through decoupling process, many effective methods have been developed over the last few years, such as, domain decomposition methods [51,52,53,54,55,56], preconditioning techniques [57], partitioned time-stepping methods [58,59,60,61], two-grid and multi-grid methods [62,63,64,65,66,67,68,69,70,71,72,73,74,75,76], Lagrange multiplier methods [7, 77, 78], discontinuous Galerkin finite element methods [6, 79, 80], finite volume methods [81, 82], mortar finite element methods [83, 84], artificial compression methods [85, 86] and many others.

The two-grid finite element method is one of the most popular technique to study a large stationary coupled problem through decoupling approach. This method was first introduced by Xu [62, 63] for the non-symmetric and nonlinear elliptic problems. Later, the two-grid method was introduced for decoupling the Stokes-Darcy fluid flow model in [64] by Mu and Xu. Cai et al. used a two-grid algorithm to solve Navier-Stokes-Darcy model in [65]. To solve the mixed Stokes-Darcy model with optimal error estimates, some modified methods are discussed and analyzed in [66,67,68]. Recently, a low order stabilized two-grid finite element method was proposed and numerically solved by Yu et al. [69] for the Stokes-Darcy fluid flow model. Moreover, Zhang et al. reported two-grid method for the Stokes-Stokes coupled problem in [70]. Two-grid method is a type of decoupling approach to solve a coupled problems into two-levels, such as in coarse grid mesh and fine grid mesh where h << H [71]. The key idea is to use a coarse grid mesh to produce the manufactured approximate solution for the linear/nonlinear problems, and then use it as the initial guess on the fine grid. Furthermore, the two-grid method provides a decoupling approach to solve the global problems into several subproblems independently by using the most appropriate numerical techniques and preconditions. Numerical results suggest that the decoupled two-grid algorithm achieves similar approximate accuracy as the coupled algorithm.

In this paper, the dual-permeability-Stokes interface system is solved numerically by using the two-grid method. To couple the Stokes equation and the dual-permeability equations, four physically valid interface conditions are utilized. The first interface condition describes the no-communication of fluid between Stokes and matrix region. Second and third interface conditions are mass conservation and balance of normal forces, respectively. The fourth interface condition is Beavers-Joseph-Saffman interface condition [87, 88]. To our best of knowledge, this is the first work to solve the stationary dual-permeability-Stokes fluid flow model through two-grid method. On the coarse mesh, a coupling problem is solved by using the standard P_k − P_k− 1 − P_k − P_k finite element approximation. On the fine mesh, three decoupled subproblems are solved independently through parallel computation as: the Stokes problem, the microfracture, and matrix equations. Moreover, the Stokes problem and microfracture equations are separated by the interface. On the other hand, microfracture and matrix equations are decoupled through the mass exchange terms. Two-grid algorithm is widely used due to its simplicity and computational flexibility, such as significant CPU time saving without losing approximate accuracy and less computer memory for meshes and algebraic systems. Furthermore, the two-grid method provides a simple way to partition a large steady-state coupled system into several subproblems, which can be computed in parallel. The variational formulation is reported, the optimal error estimate is derived for the coupled and two-grid schemes. Four numerical experiments are illustrated to validate the numerical methods and show the features of the dual-permeability-Stokes fluid flow model.

The rest of the paper is organized as follows. A dual-permeability-Stokes fluid flow model is presented in the next Section. In Section 3, a two-grid algorithm for the dual-permeability-Stokes fluid flow model is given and the optimal error estimates are derived. Four numerical experiments are presented on the support of the theoretical analysis in Section 4. Finally, a short conclusion is reported in Section 5.

2 Model equations

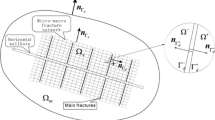
As illustrated in Fig. 1, we consider a composite domain consisting of nonoverlapping conduit subdomain Ω_c and the dual-permeability subdomain Ω_p, where Ω_c,Ω_p ⊂ R^d(d = 2 or 3) are smooth, and bounded. Here Ω_c ∩Ω_p = ∅, $\overline { {\Omega } }_{c}\cup \overline {\Omega }_{p}=\overline {\Omega }$, ∂Ω_c ∩ ∂Ω_p = Γ is the interface.

Fig. 1

The global domain Ω consisting of the conduit region Ω_c, and the dual-permeable medium Ω_p separated by the interface Γ

The below dual-permeability-Stokes fluid flow model is the steady-state version of the time-dependent dual-porosity-Stokes interface system which was studied in [23, 26, 28].

In the conduit domain Ω_c, the fluid flow is governed by the stationary Stokes equations which can be written as

$$ \begin{array}{@{}rcl@{}} - \nu {\Delta} \vec{u} +\nabla p & = & \vec{f}\quad \text{in}~{\Omega}_{c}, \end{array} $$

(2.1)

$$ \begin{array}{@{}rcl@{}} \nabla\cdot \vec{u} & = &0 \quad \text{in}~{\Omega}_{c}, \end{array} $$

(2.2)

$$ \begin{array}{@{}rcl@{}} \vec{u} & = &0 \quad \text{on}~\partial {\Omega}_{c}\setminus{\Gamma}. \end{array} $$

(2.3)

In the naturally fractured reservoir subdomain Ω_p, the fluid flow is modeled by the dual-permeability fluid flow models, which is composed of matrix and microfracture equations [23, 26] as follows:

$$ \begin{array}{@{}rcl@{}} -\nabla \cdot (\frac{k_{m}}{\mu}\nabla \varphi_{m} )&=&-\frac{\sigma k_{m}}{\mu}(\varphi_{m}-\varphi_{f})\ \ \ \text{in}\ {\Omega}_{p}, \end{array} $$

(2.4)

$$ \begin{array}{@{}rcl@{}} \varphi_{m} &=& 0 \ \ \ \text{on}\ \partial{\Omega}_{p}\setminus{\Gamma}, \end{array} $$

(2.5)

$$ \begin{array}{@{}rcl@{}} -\nabla \cdot (\frac{k_{f}}{\mu}\nabla \varphi_{f} )&=&\frac{\sigma k_{m}}{\mu}(\varphi_{m}-\varphi_{f})+q_{p} \ \ \ \text{in}\ {\Omega}_{p}, \end{array} $$

(2.6)

$$ \begin{array}{@{}rcl@{}} \varphi_{f} &=& 0 \ \ \ \text{on}\ \partial{\Omega}_{p}\setminus{\Gamma}. \end{array} $$

(2.7)

Here, $\vec {u}$ is the fluid velocity and p is the pressure, ν is the kinematic viscosity, $\vec {f}$ is the external force on the fluid domain, φ_m and φ_f are the pressure in matrix and fracture region, k_m and k_f represent the intrinsic permeability in matrix and fracture regime, μ is the dynamic viscosity. $\frac {\sigma k_{m}}{\mu }(\varphi _{m}-\varphi _{f})$ represents the mass exchange term between matrix and microfractures with σ is a shape factor characterizing the morphology and dimension of the microfractures. q_p is the sink/source term.

The matrix region is the main storage of fluid, which supplies the fluid to the fracture continua. On the other hand, the fracture region feeds the conduit or wellbore while receiving the fluid from the matrix only. Hence, the matrix block does not interact directly with the conduit or wellbore. As a result, we utilize no-communication interface condition between matrix and conduit region [23, 26]. Moreover, three traditional coupling conditions are applied to describe the interface between microfracture and conduit region. Hence, the coupling conditions for the dual-permeability-Stokes fluid flow model can be written as:

• No-communication of fluid between matrix block and conduit region:

  $$ \begin{array}{@{}rcl@{}} -\frac{k_{m}}{\mu}\nabla\varphi_{m}\cdot \hat{n}_{p}&=&0\quad\quad \text{on} {\Gamma}. \end{array} $$

  (2.8)

• The conservation of mass on the interface Γ:

  $$ \begin{array}{@{}rcl@{}} \vec{u}\cdot \hat{n}_{c} &=& \frac{k_{f}}{\mu}\nabla\varphi_{f}\cdot \hat{n}_{p} \quad\quad \text{on} {\Gamma}. \end{array} $$

  (2.9)

• Balance of normal forces on the interface Γ:

  $$ \begin{array}{@{}rcl@{}} p-\nu \hat{n}_{c} \frac{\partial \vec{u}}{\partial \hat{n}_{c}} &=&\frac{\varphi_{f}}{\rho} \quad \text{on} {\Gamma}. \end{array} $$

  (2.10)

• The Beavers-Joseph-Saffman-Jones coupling condition on the interface Γ:

  $$ \begin{array}{@{}rcl@{}} -\nu \tau_{i} \frac{\partial \vec{u}}{\partial \hat{n}_{c}} &=&\frac{\alpha \nu \sqrt{d}}{\sqrt{{\text{tr}({\Pi})}}}\vec{u}\cdot \tau_{i} \quad 1\leq i \leq (d-1) \quad \text{on} {\Gamma}, \end{array} $$

  (2.11)

where $\hat {n}_{c}$ and $\hat {n}_{p}$ denote the unit outward normal vectors on ∂Ω_c and ∂Ω_p, respectively. On the interface Γ, the unit outward normal vector satisfies $\hat {n}_{c}=-\hat {n}_{p}$. ρ is the fluid density, α is a constant parameter depending on the properties of the porous medium and τ_i(i = 1,...,d − 1) denote the unit tangential vectors on the interface Γ. π = k_fI is the intrinsic permeability of the fracture medium.

For any arbitrary domain D ⊂ R^d(d = 2,3), the L²(D) inner product and its norm are equipped with (⋅,⋅)_D and ∥⋅∥_0,D, respectively. The norm of the Hilbert spaces H^k(D) can be denoted by ∥⋅∥_k,D, for scalar and vector-valued functions.

Define the following spaces:

$$ \begin{array}{@{}rcl@{}} H_{c} &=& \{\vec{v} \in (H^{1}({\Omega}_{c}))^{d}: \vec{v}=0 \text{on} \partial{\Omega}_{c}\setminus{\Gamma}\},\\ H_{pf} &= &\{\varphi_{f} \in H^{1}({\Omega}_{p}): \varphi_{f}=0 \text{on} \partial {\Omega}_{p} \setminus{\Gamma}\},\\ H_{pm} &= &\{\varphi_{m} \in H^{1}({\Omega}_{p}): \varphi_{m}=0 \text{on} \partial {\Omega}_{p} \setminus{\Gamma}\},\\ W&=&H_{c} \times H_{pf}\times H_{pm},\\ Q&=&L^{2}({\Omega}_{c}). \end{array} $$

The space W is equipped with the following norm: $\forall \textbf {u}=(\vec {u},\varphi _{f}, \varphi _{m})\in W$,

$$ \begin{array}{@{}rcl@{}} & \|\textbf{u}\|_{0}= \left( \|\vec{u}\|^{2}_{0,{\Omega}_{c}}+\|\varphi_{f}\|^{2}_{0,{\Omega}_{p}}+\|\varphi_{m}\|^{2}_{0,{\Omega}_{p}}\right)^{1/2} . \end{array} $$

(2.12)

The weak formulation of the dual-permeability-Stokes fluid flow model (2.1)–(2.11) is as follows: find $\textbf {u}=(\vec {u},\varphi _{f}, \varphi _{m})\in W$ and p ∈ Q such that

$$ \begin{array}{@{}rcl@{}} a(\textbf{u},\textbf{v}) +b(\textbf{v},p)&=&(\textbf{f},\textbf{v}) \quad\forall \textbf{v}=(\vec{v},\psi_{f},\psi_{m})\in W, \end{array} $$

(2.13)

$$ \begin{array}{@{}rcl@{}} b(\textbf{u},q)&=&0 \quad\qquad \forall q \in Q, \end{array} $$

(2.14)

where

$$ \begin{array}{@{}rcl@{}} a(\textbf{u},\textbf{v}) &= &a_{\Omega}(\textbf{u},\textbf{v})+ a_{\Gamma}(\textbf{u},\textbf{v})+a_{fm}(\textbf{u},\textbf{v}),\\ a_{\Omega}(\textbf{u},\textbf{v})&=&a_{c}(\vec{u},\vec{v})+a_{f}(\varphi_{f},\psi_{f})+a_{m}(\varphi_{m},\psi_{m}),\\ a_{\Gamma}(\textbf{u},\textbf{v})&=& {\int}_{\Gamma}(\frac{1}{\rho}\varphi_{f} \vec{v} \cdot \hat{n}_{c} - \psi_{f} \vec{u} \cdot \hat{n}_{c})ds,\\ a_{fm}(\textbf{u},\textbf{v})&=&-\frac{\sigma k_{m}}{\mu}(\varphi_{f} \psi_{m} + \varphi_{m} \psi_{f})_{{\Omega}_{p}},\\ a_{c}(\vec{u},\vec{v})&=&\nu(\nabla \vec{u}, \nabla \vec{v})_{{\Omega}_{c}}+ \frac{\alpha \nu\sqrt{d}}{\sqrt{{\text{tr}(\mathbf{\Pi})}}}{\sum}_{i=1}^{d-1}{\int}_{\Gamma} ({\vec{u} }\cdot \tau_{i})(\vec{v}\cdot\tau_{i})ds,\\ a_{f}(\varphi_{f},\psi_{f})&=&\frac{k_{f}}{\mu}(\nabla \varphi_{f},\nabla \psi_{f})_{{\Omega}_{p}}+\frac{\sigma k_{m}}{\mu}(\varphi_{f},\psi_{f} )_{{\Omega}_{p}},\\ a_{m}(\varphi_{m},\psi_{m})&=&\frac{k_{m}}{\mu}(\nabla \varphi_{m},\nabla \psi_{m})_{{\Omega}_{p}}+\frac{\sigma k_{m}}{\mu}(\varphi_{m},\psi_{m} )_{{\Omega}_{p}},\\ b(\textbf{v},p)&=& - (p,\nabla \cdot {\vec{v}} )_{{\Omega}_{c}},\\ (\textbf{f},\textbf{v}) &=&(\vec{f},\vec{v})_{{\Omega}_{c} } + (q_{p},\psi_{f})_{{\Omega}_{p} }. \end{array} $$

The well-posedness of the dual-permeability-Stokes fluid flow model can be easily derived by following [23].

3 Decoupled scheme and error estimates

In this section, two-grid decoupled algorithm and the error estimates are presented for the dual-permeability-Stokes model.

Let ${{\Pi }^{h}_{i}}$ be a regular triangulation of Ω_i,i = c,p consisting of K elements with mesh size function h(x), whose value is the diameter B_T. Let W_h = H_c,h × H_pf,h × H_pm,h ⊂ W and Q_h ⊂ Q be the finite element subspaces.

For the finite element spaces H_c,h × H_pf,h × H_pm,h × Q_h, the following error estimates for the dual-porosity-Stokes model holds: $\forall (\vec {v}, \psi _{f}, \psi _{m}, q) \in W({\Omega }) \times H^{1}({\Omega })$ there exists approximation $I_{h}\vec {v} \in H_{c,h}$, L_hψ_f ∈ H_pf,h, J_hψ_m ∈ H_pm,h and ρ_hq ∈ Q_h

$$ \begin{array}{@{}rcl@{}} \Vert \vec{v}- I_{h}\vec{v}\Vert_{0,{\Omega}_{c}} + h\Vert \vec{v}- I_{h} \vec{v}\Vert_{1,{\Omega}_{c}} & \leq & ch^{2} \Vert \vec{v} \Vert_{2,{\Omega}_{c}} \end{array} $$

(3.1)

$$ \begin{array}{@{}rcl@{}} \Vert \psi_{f}- L_{h} \psi_{f}\Vert_{0,{\Omega}_{p}} + h\Vert \psi_{f}- L_{h} \psi_{f}\Vert_{1,{\Omega}_{p}} & \leq & ch^{2} \Vert \psi_{f} \Vert_{2,{\Omega}_{p}} \end{array} $$

(3.2)

$$ \begin{array}{@{}rcl@{}} \Vert \psi_{m}- J_{h} \psi_{m}\Vert_{0,{\Omega}_{p}} + h\Vert \psi_{m}- L_{h} \psi_{m}\Vert_{1,{\Omega}_{p}} & \leq & ch^{2} \Vert \psi_{m} \Vert_{2,{\Omega}_{p}} \end{array} $$

(3.3)

$$ \begin{array}{@{}rcl@{}} \Vert q- \rho_{h} q \Vert_{0,{\Omega}_{c}} & \leq & ch \Vert q \Vert_{1,{\Omega}_{c}}, \end{array} $$

(3.4)

where mapping $\rho _{h} : Q \rightarrow Q_{h}$ satisfies (p − ρ_hp,q) = 0, p ∈ Q and q ∈ Q_h.

The coupled finite element algorithm for (2.13)–(2.14) based on the subspaces (W_h,Q_h) follows:

3.1 Coupled finite element scheme

Algorithm 1 (Coupled scheme): To find $\textbf {u}_{h}=(\vec {u}_{h},\varphi _{fh},\varphi _{mh})\in W_{h}$ and p_h ∈ Q_h such that we have

$$ \begin{array}{@{}rcl@{}} a(\textbf{u}_{h},\textbf{v}_{h}) +b(\textbf{v}_{h},p_{h})&=& (\textbf{f},\textbf{v}_{h}) \ \ \ \ \forall \textbf{v}_{h}=(\vec{v}_{h},\psi_{fh},\psi_{mh})\in W_{h}, \end{array} $$

(3.5)

$$ \begin{array}{@{}rcl@{}} b(\textbf{u}_{h},q_{h}) &=&0 \ \ \ \forall q_{h} \in Q_{h}. \end{array} $$

(3.6)

Remark 3.1

For convenience, we rewrite the variational form (2.13)–(2.14) by using the bilinear form as an equivalent formulation

$$ \begin{array}{@{}rcl@{}} \mathcal{B} \left( (\vec{u}, \varphi_{f}, \varphi_{m}, p),(\vec{v},\psi_{f}, \psi_{m}, q)\right)= (\textbf{f},\textbf{v}), \end{array} $$

(3.7)

and the coupled scheme (3.5)–(3.6) can be written as

$$ \begin{array}{@{}rcl@{}} \mathcal{B}_{h} \left( (\vec{u}_{h}, \varphi_{fh}, \varphi_{mh}, p_{h}),(\vec{v}_{h},\psi_{fh}, \psi_{mh}, q_{h})\right)= (\textbf{f},\textbf{v}_{h}), \end{array} $$

(3.8)

to derive the stability and convergence of the coupled algorithm.

Theorem 3.1

The bilinear form ${\mathscr{B}}_{h} \left ((\vec {u}_{h}, \varphi _{fh}, \varphi _{mh}, p_{h}),(\vec {v}_{h},\psi _{fh}, \psi _{mh}, q_{h})\right )$ satisfies the continuity

$$ \begin{array}{@{}rcl@{}} &&\mathcal{B}_{h} \left( (\vec{u}_{h}, \varphi_{fh}, \varphi_{mh}, p_{h}),(\vec{v}_{h},\psi_{fh}, \psi_{mh}, q_{h})\right)\\ &\leq& c\left( \parallel\vec{u}_{h}\parallel_{1} +\parallel\varphi_{fh}\parallel_{1} + \parallel \varphi_{mh}\parallel_{1} +\parallel p_{h}\parallel_{0}\right) \\ &&\left( \parallel\vec{v}_{h}\parallel_{1} +\parallel\psi_{fh}\parallel_{1}+ \parallel\psi_{mh}\parallel_{1}+\parallel q_{h}\parallel_{0}\right) \\ &&\forall (\vec{u}_{h}, \varphi_{fh}, \varphi_{mh}, p_{h}), (\vec{v}_{h}, \psi_{fh}, \psi_{mh}, q_{h}) \in (W_{h}, Q_{h}), \end{array} $$

(3.9)

and the coercivity

$$ \begin{array}{@{}rcl@{}} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\sup_{0\neq (\vec{v}_{h}, \psi_{fh}, \psi_{mh}, q_{h})\in (W_{h}, Q_{h})} \frac{\mid \mathcal{B}_{h}\left( (\vec{u}_{h}, \varphi_{fh}, \varphi_{mh}, p_{h}),(\vec{v}_{h}, \psi_{fh}, \psi_{mh}, q_{h})\right)\mid}{\left( \parallel\vec{v}_{h}{\parallel_{1}^{2}}+\parallel\psi_{fh}{\parallel_{1}^{2}}+\parallel\psi_{mh}{\parallel_{1}^{2}}+\parallel q_{h}{\parallel_{0}^{2}}\right)^{\frac{1}{2}}} \\ \geq \beta \left( \parallel\vec{u}_{h}{\parallel_{1}^{2}}+\parallel\varphi_{fh}{\parallel_{1}^{2}}+\parallel\varphi_{mh}{\parallel_{1}^{2}}+\parallel p_{h}{\parallel_{0}^{2}}\right)^{\frac{1}{2}}, \end{array} $$

(3.10)

where β is a positive constant depending only on Ω.

Remark 3.2

By following [23, 64, 69, 74, 89], the continuity and coercivity for the coupled scheme of the dual-permeability-Stokes fluid flow model can be achieved. To prove the stability for the coupled system of the dual-permeability-Stokes interface system is not our main concern. Moreover, for this coupled system, one needs to solve a global problem, which produces huge complexities in solving the resulting linear systems. Therefore, a two-grid method is designed to solve a large system by decoupling the coupled problem into several parallel subproblems in the following way.

3.2 Two-grid decoupled scheme

Algorithm 2 (Two-grid scheme):

Step 1. Firstly, we solve the coupled finite element problem on a coarse grid H. To find $\textbf {u}_{H}=(\vec {u}_{H},\varphi _{fH},\varphi _{mH})\in W_{H}\subset W_{h}$ and p_H ∈ Q_H ⊂ Q_h such that

$$ \begin{array}{@{}rcl@{}} a(\textbf{u}_{H},\textbf{v}_{H}) +b(\textbf{v}_{H},p_{H}) &= &(\textbf{f},\textbf{v}_{H})\quad \forall \textbf{v}_{H}=(\vec{v}_{H},\psi_{fH},\psi_{mH})\in W_{H}, \end{array} $$

(3.11)

$$ \begin{array}{@{}rcl@{}} b(\textbf{u}_{H},q_{H})&=&0 \quad \forall q_{H} \in Q_{H}. \end{array} $$

(3.12)

Step 2. Using the approximate solution of the coarse grid, we solve three decoupled subproblems in the fine grid h << H. To find $\textbf {u}^{h}=(\vec {u}^{h},{\varphi _{f}^{h}},{\varphi _{m}^{h}}) \in W_{h}, {p}^{h} \in Q_{h}$ such that

$$ \begin{array}{@{}rcl@{}} a_{\Omega}(\textbf{u}^{h},\textbf{v}_{h}) +b(\textbf{v}_{h},p^{h}) &=& (\textbf{f},\textbf{v}_{h})- a_{\Gamma}(\textbf{u}_{H},\textbf{v}_{h})-a_{fm}(\textbf{u}_{H},\textbf{v}_{h})\\ &&\quad\forall \textbf{v}_{h}=(\vec{v}_{h},\psi_{fh},\psi_{mh})\in W_{h}, \end{array} $$

(3.13)

$$ \begin{array}{@{}rcl@{}} b(\textbf{u}^{h},q_{h})&=&0 \forall q_{h} \in Q_{h}. \end{array} $$

(3.14)

It is not difficult to verify that the system (3.13)–(3.14) is equivalent to three decoupled subproblems: one is a Stokes problem on Ω_c and the other two are the matrix and microfracture equations on Ω_p. In fact, on the fine grid, the discrete Stokes problem is solved in Ω_c: find ${\vec {u}}^{h} \in H_{c,h}, {p}^{h} \in Q_{h}$ such that

$$ \begin{array}{@{}rcl@{}} a_{c}({\vec{u}}^{h},\vec{v}_{h}) + b(\vec{v}_{h}, {p}^{h}) & = & (\vec{f},\vec{v}_{h})_{{\Omega}_{c}} - {\int}_{\Gamma} \frac{1}{\rho}{\varphi}_{fH} \vec{v}_{h}\cdot \hat{n}_{c} ds \quad \forall \vec{v}_{h} \in H_{c,h}, \end{array} $$

(3.15)

$$ \begin{array}{@{}rcl@{}} b({\vec{u}}^{h},q_{h})&=&0 \ \ \quad \forall q_{h} \in Q_{h}. \end{array} $$

(3.16)

And in the porous flow domain Ω_p, we only need to solve the matrix and microfracture equations in parallel: find ${\varphi }_{m}^{h} \in H_{pm,h}$ such that

$$ \begin{array}{@{}rcl@{}} a_{m}({\varphi}_{m}^{h}, \psi_{mh})&=& \frac{\sigma k_{m}}{\mu}(\varphi_{fH},\psi_{mh})\quad \forall \psi_{mh} \in H_{pm,h}, \end{array} $$

(3.17)

and find ${\varphi }_{f}^{h} \in H_{pf,h}$ such that

$$ \begin{array}{@{}rcl@{}} a_{f}({\varphi}_{f}^{h}, \psi_{fh})&=&\frac{\sigma k_{m}}{\mu}(\varphi_{mH},\psi_{fh})+(q_{p}, \psi_{fh})_{{\Omega}_{p}}\\&&+ {\int}_{\Gamma} \psi_{fh} \vec{u}_{H}\cdot \hat{n}_{c} ds \quad\forall \psi_{fh} \in H_{pf,h}. \end{array} $$

(3.18)

3.3 Error estimates

This section deals with the optimal convergence analysis of the proposed coupled scheme and two-grid method for the dual-permeability-Stokes fluid flow model. Hence, the present analysis is carried out for Algorithm 1 and Algorithm 2.

The following error estimates hold for $(\vec {u}_{h},p_{h},\varphi _{fh},\varphi _{mh})$ by assuming the regularity $\vec {u}\in (H^{2}({\Omega }_{c}))^{2}, {\varphi _{f}} \in H^{2}({\Omega }_{p}),{\varphi _{m}} \in H^{2}({\Omega }_{p})$ and $p\in H^{1}({\Omega }_{c})$ for Algorithm 1 [23, 64, 69, 73, 74, 89].

Theorem 3.2

$$ ||\vec{u}-\vec{u}_{h}||_{1,{\Omega}_{c}} + ||\varphi_{f}-\varphi_{fh}||_{1,{\Omega}_{p}} + ||\varphi_{m}-\varphi_{mh}||_{1,{\Omega}_{p}}+||p-p_{h}||_{0,{\Omega}_{c}}\leq c h, $$

(3.19)

and

$$ ||\vec{u}-\vec{u}_{h}||_{0,{\Omega}_{c}} +{ ||\varphi_{f}-\varphi_{fh}||_{0,{\Omega}_{p}}} +{ ||\varphi_{m}-\varphi_{mh}||_{0,{\Omega}_{p}}}\leq c h^{2}. $$

(3.20)

Consequently, on the coarse mesh, one can obtain

$$ \begin{array}{ll} &||\vec{u}-\vec{u}_{H}||_{0,{\Omega}_{c}} +{ ||\varphi_{f}-\varphi_{fH}||_{0,{\Omega}_{p}}}+{ ||\varphi_{m}-\varphi_{mH}||_{0,{\Omega}_{p}}} \\ &\qquad{}+H\left( ||\vec{u}-\vec{u}_{H}||_{1,{\Omega}_{c}} +{ ||\varphi_{f}-\varphi_{fH}||_{1,{\Omega}_{p}} } +{ ||\varphi_{m}-\varphi_{mH}||_{1,{\Omega}_{p}} }\right.\\&\qquad \left.+ ||p-p_{H}||_{0,{\Omega}_{c}}\right)\leq c H^{2}. \end{array} $$

(3.21)

proof

Setting $(\vec {v}, \psi _{f}, \psi _{m}, q) = (\vec {v}_{h}, \psi _{fh}, \psi _{mh}, q_{h})$ in (3.7) and subtracting (3.7) from (3.8), we obtain

$$ \begin{array}{@{}rcl@{}} \!\!\!\!\!\!\!\!\!\!\!\!\mathcal{B}_{h}\left( (\vec{u} - \vec{u}_{h}), (\varphi_{f} - \varphi_{fh}), (\varphi_{m} - \varphi_{mh}), (p - p_{h})), (\vec{v}_{h}, \psi_{fh}, \psi_{mh}, q_{h})\right)=0. \end{array} $$

(3.22)

By plugging interpolation error $(\vec {e}, \zeta , \xi , \eta )= (I_{h}\vec {u}-\vec {u}_{h}, L_{h}\varphi _{f}-\varphi _{fh}, J_{h}\varphi _{m}-\varphi _{mh}, \rho _{h}p-p_{h} )$, using the estimates (3.1)–(3.4) and the continuity (3.9), we obtain

$$ \begin{array}{@{}rcl@{}} &&\mathcal{B}_{h}\left( (\vec{e}, \zeta, \xi, \eta),(\vec{v}_{h}, \psi_{fh}, \psi_{mh}, q_{h})\right)\\ & = & -\mathcal{B}_{h}\left( (\vec{u}-I_{h}\vec{u}, \varphi_{f}-L_{h}\varphi_{f}, \varphi_{m}-J_{h}\varphi_{m}, p-\rho_{h}p),(\vec{v}_{h}, \psi_{fh}, \psi_{mh}, q_{h})\right) \\ &\leq& \mid \mathcal{B}_{h}((\vec{u}-I_{h}\vec{u}, \varphi_{f}-L_{h}\varphi_{f}, \varphi_{m}-J_{h}\varphi_{m}, p-\rho_{h}p),(\vec{v}_{h}, \psi_{fh}, \psi_{mh}, q_{h}))\mid \\& \leq& c \left( \parallel \vec{u}-I_{h}\vec{u} \parallel_{1, {\Omega}_{c}}+\parallel \varphi_{f}-L_{h}\varphi_{f}\parallel_{1, {\Omega}_{p}} +\parallel \varphi_{m}-J_{h}\varphi_{m}\parallel_{1, {\Omega}_{p}} \right.\\ &&\left.+\parallel p-\rho_{h}p\parallel_{0, {\Omega}_{c}}\right) \left( \parallel \vec{v}_{h}\parallel_{1, {\Omega}_{c}}+\parallel\psi_{fh}\parallel_{1, {\Omega}_{p}}+\parallel \psi_{mh}\parallel_{1,{\Omega}_{p}}+\parallel q_{h}\parallel_{0,{\Omega}_{c}}\right) \\& \leq& ch\left( \parallel \vec{u}\parallel_{2,{\Omega}_{c}}+\parallel \varphi_{f}\parallel_{2,{\Omega}_{p}}+\parallel\varphi_{m}\parallel_{2, {\Omega}_{p}}+\parallel p_{h}\parallel_{1, {\Omega}_{c}}\right) \\ & & \left( \parallel\vec{v}_{h}\parallel_{1,{\Omega}_{c}}+\parallel\psi_{fh}\parallel_{1,{\Omega}_{p}}+\parallel\psi_{mh}\parallel_{1,{\Omega}_{p}}+\parallel q_{h}\parallel_{0,{\Omega}_{c}}\right). \end{array} $$

(3.23)

Now

$$ \begin{array}{@{}rcl@{}} &&\beta \left( \parallel \vec{e} \parallel^{2}_{1,{\Omega}_{c}}+\parallel\zeta \parallel^{2}_{1,{\Omega}_{p}}+\parallel \xi \parallel^{2}_{1,{\Omega}_{p}}+\parallel \eta \parallel^{2}_{0,{\Omega}_{c}}\right)^{\frac{1}{2}} \\ &\leq& \sup_{0\neq (\vec{v}_{h},\psi_{fh}, \psi_{mh}, q_{h}) \in (W_{h}, Q_{h})} \frac{\mid \mathcal{B}_{h}((\vec{e},\zeta, \xi, \eta),(\vec{v}_{h}, \psi_{fh},\psi_{mh}, q_{h}))\mid} {\left( \parallel\vec{v}_{h}\parallel_{1, {\Omega}_{c}}^{2}+\parallel \psi_{fh}\parallel_{1, {\Omega}_{p}}^{2}+\parallel \psi_{mh} \parallel_{1, {\Omega}_{p}}^{2}+\parallel q_{h}\parallel_{0, {\Omega}_{c}}^{2}\right)^{\frac{1}{2}}} \\ &\leq& ch\left( \parallel \vec{u}\parallel_{2,{\Omega}_{c} }+ \parallel \varphi_{f}\parallel_{2,{\Omega}_{p}}+ \parallel \varphi_{m}\parallel_{2, {\Omega}_{p}}+ \parallel p \parallel_{1,{\Omega}_{p}}\right), \end{array} $$

(3.24)

the use of triangle inequality

$$ \begin{array}{@{}rcl@{}} && \parallel \vec{u}-\vec{u}_{h}\parallel_{1,{\Omega}_{c}}+\parallel \varphi_{f}-\varphi_{fh}\parallel_{1, {\Omega}_{p}}+\parallel \varphi_{m}-\varphi_{mh}\parallel_{1,{\Omega}_{p}}+ \parallel p-p_{h}\parallel_{0,{\Omega}_{c}} \\ &\leq& ch\left( \parallel \vec{u}\parallel_{2, {\Omega}_{c}}+\parallel \varphi_{f} \parallel_{2, {\Omega}_{p}}+\parallel \varphi_{m}\parallel_{2, {\Omega}_{p}}+\parallel p\parallel_{1,{\Omega}_{p}}\right), \end{array} $$

(3.25)

which provides the desired H¹(Ω) error estimate (3.19).

We define discrete divergence free space $V= \lbrace \vec {v} \in H_{c}~ \mathrm {such~ that~} \text {div} \vec {v}=0 ~\text {in}~ {\Omega }_{c} \rbrace$.

Let $(\vec {u}, \varphi _{f}, \varphi _{m}, p)$ and $(\vec {u}_{h}, \varphi _{fh}, \varphi _{mh}, p_{h})$ be the solution of (3.7) and (3.8), respectively. Find $(\vec {w}, \xi _{f}, \xi _{m}, r) \in V \times H_{pf} \times H_{pm}\times Q$ such that $(\vec {v}, \psi _{f}, \psi _{m}, q)\in (W, Q)$ satisfies

$$ \begin{array}{@{}rcl@{}} \!\!\!\!\!\!\!\!\!&&\mathcal{B}\left( (\vec{v}, \psi_{f}, \psi_{m}, q), (\vec{w}, \xi_{f}, \xi_{m}, r)\right)\\ \!\!\!\!\!\!\!\!\!\!&=& {\int}_{{\Omega}_{c}} (\vec{u}-\vec{u}_{h}) \vec{v}dx+{\int}_{{\Omega}_{p}} (\varphi_{f}-\varphi_{fh})\psi_{f}dx+ {\int}_{{\Omega}_{p}} (\varphi_{m}-\varphi_{mh})\psi_{m}dx. \end{array} $$

(3.26)

The solution of the dual-problem achieves the following regularity condition

$$ \begin{array}{@{}rcl@{}} &&\parallel \vec{w} \parallel_{2, {\Omega}_{c}}+ \parallel \xi_{f} \parallel_{2, {\Omega}_{p}}+ \parallel \xi_{m} \parallel_{2, {\Omega}_{p}}+ \parallel r \parallel_{1, {\Omega}_{p}} \\ &\leq& c\left( \parallel \vec{u}-\vec{u}_{h} \parallel_{0, {\Omega}_{c}}+ \parallel \varphi_{f}-\varphi_{f} \parallel_{0, {\Omega}_{p}}+ \parallel \varphi_{m}-\varphi_{m} \parallel_{0, {\Omega}_{p}}\right). \end{array} $$

(3.27)

Plugging $(\vec {v}, \psi _{f}, \psi _{m}, q) = (\vec {u}-\vec {u}_{h}, \varphi _{f}-\varphi _{fh}, \varphi _{m}-\varphi _{mh}, p-p_{h})$ in the dual-problem (3.26) and using (3.1)–(3.4), continuity result (3.9), equation (3.25), we can get

$$ \begin{array}{@{}rcl@{}} && \parallel \vec{u}-\vec{u}_{h}\parallel^{2}_{0, {\Omega}_{c}}+\parallel\varphi_{f}-\varphi_{fh}\parallel^{2}_{0, {\Omega}_{p}} +\parallel \varphi_{m}-\varphi_{mh}\parallel^{2}_{0, {\Omega}_{p}} \\ &=& \mathcal{B}\left( (\vec{w},\xi_{f},\xi_{m},r),(\vec{u}-\vec{u}_{h}, \varphi_{f}-\varphi_{fh}, \varphi_{m}-\varphi_{mh}, p-p_{h})\right) \\ &\leq& \mathcal{B}\left( (\vec{w}-I_{h}\vec{w}, \xi_{f}-L_{h}\xi_{f}, \xi_{m}-J_{h}\xi_{m}, r-\rho_{h}r),(\vec{u}-\vec{u}_{h}, \varphi_{f}-\varphi_{fh},\right. \\ &&\left.\varphi_{m}-\varphi_{mh}, p-\rho_{h}p)\right)+\mathcal{B}\left( (I_{h}\vec{w}, L_{h}\xi_{f}, J_{h}\xi_{m}, \rho_{h}r), (\vec{u}-\vec{u}_{h},\right. \\ &&\left.\varphi_{f}-\varphi_{fh}, \varphi_{m}-\varphi_{mh},p-p_{h})\right) \\ &\leq& \left( \parallel\vec{u}-\vec{u}_{h} \parallel_{1, {\Omega}_{c}} \parallel \vec{w}-I_{h}\vec{w} \parallel_{1, {\Omega}_{c}}+ \parallel \varphi_{f}-\varphi_{fh} \parallel_{1, {\Omega}_{p}}\parallel \xi_{f}-L_{h}\xi_{f}\parallel_{1, {\Omega}_{p}}\right. \\ &&+ \parallel \varphi_{m}-\varphi_{mh}\parallel_{1,{\Omega}_{p}}\parallel\xi_{m}-J_{h}\xi_{m}\parallel_{1, {\Omega}_{p}} +\parallel \vec{w}-I_{h}\vec{w}\parallel_{1,{\Omega}_{c}}\parallel p-p_{h}\parallel_{0, {\Omega}_{c}} \\ &&+\parallel \vec{w}-I_{h}\vec{w} \parallel_{1, {\Omega}_{c}}\parallel \varphi_{m}-\varphi_{mh}\parallel_{1,{\Omega}_{p}}+\parallel \vec{w}-I_{h}\vec{w}\parallel_{1,{\Omega}_{c}}\parallel \varphi_{f}-\varphi_{fh}\parallel_{1,{\Omega}_{p}} \\ &&+ \parallel \vec{u}-\vec{u}_{h} \parallel_{1,{\Omega}_{p}}\parallel \xi_{m}-J_{h}\xi_{m}\parallel_{1, {\Omega}_{p}}+\parallel \vec{u}-\vec{u}_{h} \parallel_{1,{\Omega}_{c}}\parallel \xi_{f}-L_{h}\xi_{f} \parallel_{1, {\Omega}_{p}} \\ &&+ \parallel \varphi_{f}-\varphi_{fh}\parallel_{1,{\Omega}_{p}} \parallel \xi_{m}-J_{h}\xi_{m}\parallel_{1, {\Omega}_{p}} + \parallel \varphi_{m}-\varphi_{mh}\parallel_{1,{\Omega}_{p}}\parallel \xi_{f}-L_{h}\xi_{f} \parallel_{1, {\Omega}_{p}} \\ &&\left.+\parallel \vec{u}-\vec{u}_{h} \parallel_{1,{\Omega}_{c}}\parallel r-\rho_{h}r\parallel_{0,{\Omega}_{c}}+\parallel p-p_{h}\parallel_{0,{\Omega}_{c}} \parallel r-\rho_{h}r\parallel_{0,{\Omega}_{c}}\right) \\ &\leq& ch\left( \parallel\vec{u}-\vec{u}_{h} \parallel_{1,{\Omega}_{c}}^{2}+\parallel \varphi_{f}-\varphi_{fh} \parallel_{1,{\Omega}_{p}}^{2}+\parallel \varphi_{m}-\varphi_{mh}\parallel_{1,{\Omega}_{p}}^{2}\right. \\ &&\left.+\parallel p-p_{h}\parallel_{0,{\Omega}_{p}}^{2}\right)^{\frac{1}{2}}\left( \parallel \vec{w} \parallel_{2,{\Omega}_{c}}^{2}+\parallel\xi_{f}\parallel^{2}_{2,{\Omega}_{p}}+\parallel \xi_{m} \parallel^{2}_{2,{\Omega}_{p}}+\parallel r \parallel_{1,{\Omega}_{c}}^{2}\right)^{\frac{1}{2}} \\ &\leq& ch^{2} \left( \parallel \vec{u}\parallel_{2,{\Omega}_{c}}+\parallel \varphi_{f}\parallel_{2,{\Omega}_{p}}+\parallel\varphi_{m}\parallel_{2,{\Omega}_{p}}+\parallel p\parallel_{1,{\Omega}_{c}}\right) \\ &&\left( \parallel \vec{w} \parallel_{2,{\Omega}_{c}}^{2}+\parallel\xi_{f}\parallel^{2}_{2,{\Omega}_{p}}+\parallel \xi_{m} \parallel^{2}_{2,{\Omega}_{p}}+\parallel r \parallel_{1,{\Omega}_{c}}^{2}\right)^{\frac{1}{2}}, \end{array} $$

(3.28)

finally, the results (3.20) follows by (3.27).

On the other hand, the estimate for the coarse mesh (3.21) can be obtained immediately from the above H¹(Ω) and L²(Ω) error estimate by replacing h by H. □

Next, we derive the error estimate for the two-grid method of the dual-permeability-Stokes fluid flow model.

Theorem 3.3

Let $(\vec {u}_{h},p_{h},{\varphi }_{fh},{\varphi }_{mh})$ and $(\vec {u}^{h},p^{h},{\varphi ^{h}_{f}},{\varphi }^{h}_{m})$ be the solutions of Algorithm 1 and Algorithm 2, respectively. Then the following error estimates hold

$$ \begin{array}{@{}rcl@{}} ||\varphi_{fh}-{\varphi_{f}^{h}}||_{1,{\Omega}_{p}} +||\varphi_{mh}-{\varphi^{h}_{m}}||_{1,{\Omega}_{p}}&\leq c H^{2}, \end{array} $$

(3.29)

$$ \begin{array}{@{}rcl@{}} ||\vec{u}_{h}-\vec{u}^{h}||_{1,{\Omega}_{c}}+||p_{h}-p^{h}||_{0,{\Omega}_{c}}&\leq c H^{2} . \end{array} $$

(3.30)

proof

To derive the error estimates of the proposed two-grid method, the idea of Mu and Xu [64] is followed by comparing Algorithm 1 and Algorithm 2 on the same fine grid h, we obtain

$$ \begin{array}{@{}rcl@{}} a_{\Omega}(\textbf{u}_{h}-\textbf{u}^{h},\textbf{v}_{h})+a_{\Gamma}(\textbf{u}_{h}-\textbf{u}_{H},\textbf{v}_{h})+a_{fm}(\textbf{u}_{h}-\textbf{u}_{H},\textbf{v}_{h}) +b(\textbf{v}_{h},p_{h}-p^{h}) = &0\quad \forall \textbf{v}_{h} \in W_{h}, \end{array} $$

(3.31)

$$ \begin{array}{@{}rcl@{}} b(\textbf{u}_{h}-\textbf{u}^{h},q_{h}) = &0\quad \forall q_{h} \in Q_{h}. \end{array} $$

(3.32)

Plugging $\textbf {v}_{h}=(0,0,{\varphi }_{fh}- {\varphi }_{f}^{h})$ into the equation (3.31), we get

$$ \begin{array}{@{}rcl@{}} &&a_{f}({\varphi}_{fh}- {\varphi}_{f}^{h}, {\varphi}_{fh}- {\varphi}_{f}^{h})\\&=&\frac{\sigma k_{m}}{\mu}(\varphi_{mh}-\varphi_{mH},{\varphi}_{fh}- {\varphi}_{f}^{h}) \\&&+{\int}_{\Gamma} ({\varphi}_{fh}- {\varphi}_{f}^{h}) (\vec{u}_{h}- \vec{u}_{H})\cdot \hat{n}_{c} ds. \end{array} $$

(3.33)

It is easy to estimate the first term in the right-hand side of (3.33)

$$ \begin{array}{@{}rcl@{}} &&\frac{\sigma k_{m}}{\mu}(\varphi_{mh}-\varphi_{mH},{\varphi}_{fh}- {\varphi}_{f}^{h})\\&\leq& c ||\varphi_{mh}-\varphi_{mH}||_{0,{\Omega}_{p}}||{\varphi}_{fh}- {\varphi}_{f}^{h}||_{0,{\Omega}_{p}}\\&\leq& cH^{2}||{\varphi}_{fh}- {\varphi}_{f}^{h}||_{1,{\Omega}_{p}}. \end{array} $$

To estimate the second term in the right-hand side of (3.33), an auxiliary problem is restated which is given in [64, 69, 74]. Let $\theta \in H^{1}({\Omega }_{c})$ satisfy the following equations:

$$ \begin{array}{@{}rcl@{}} -{\Delta} \theta & = & 0\quad \mathrm{ in} {\Omega}_{c}, \end{array} $$

(3.34)

$$ \begin{array}{@{}rcl@{}} \theta &= & {\varphi}_{fh}- {\varphi}_{f}^{h}\quad \text{on} {\Gamma}, \end{array} $$

(3.35)

$$ \begin{array}{@{}rcl@{}} \theta &= & 0 \quad \text{on} \partial {\Omega}_{c}/ {\Gamma}. \end{array} $$

(3.36)

Let us suppose that $H_{00}^{1/2}({\Gamma })=[L^{2}({\Gamma }),{H^{1}_{0}}({\Gamma })]_{1/2}$ be the interpolation space [70]. Then we have the following inequalities:

$$ \begin{array}{@{}rcl@{}} ||\theta||_{1,{\Omega}_{c}}\leq c ||{\varphi}_{fh}- {\varphi}_{f}^{h} ||_{H_{00}^{1/2}({\Gamma})}\leq c ||{\varphi}_{fh}- {\varphi}_{f}^{h} ||_{1,{\Omega}_{p}}. \end{array} $$

(3.37)

For all q_H ∈ Q_H, $b(\vec {u}_{h}-\vec {u}_{H},q_{H})=0$, thus, let 𝜃_H be the interpolation of 𝜃 from Q onto Q_H, then,

$$ \begin{array}{@{}rcl@{}} &&{\int}_{\Gamma} ({\varphi}_{fh}- {\varphi}_{f}^{h}) (\vec{u}_{h}- \vec{u}_{H})\cdot \hat{n}_{c} ds \end{array} $$

(3.38)

$$ \begin{array}{@{}rcl@{}} &=& {\int}_{\partial {\Omega}_{c}}\theta (\vec{u}_{h}- \vec{u}_{H})\cdot \hat{n}_{c} ds \\ &=& {\int}_{{\Omega}_{c}}\nabla \theta \cdot (\vec{u}_{h}- \vec{u}_{H}) dx +{\int}_{{\Omega}_{c}} \theta \nabla\cdot (\vec{u}_{h}- \vec{u}_{H})dx \\ &=& {\int}_{{\Omega}_{c}}\nabla \theta \cdot (\vec{u}_{h}- \vec{u}_{H}) dx + {\int}_{{\Omega}_{c}} (\theta-\theta_{H}) \nabla\cdot (\vec{u}_{h}- \vec{u}_{H})dx \\ &\leq& c ||\vec{u}_{h}- \vec{u}_{H}||_{0,{\Omega}_{c}}||\theta||_{1,{\Omega}_{c}}+c ||\theta-\theta_{H}||_{0,{\Omega}_{c}}||\vec{u}_{h}- \vec{u}_{H}||_{1,{\Omega}_{c}}\\ &\leq& c H^{2} ||\theta||_{1,{\Omega}_{c}}\\ &\leq& cH^{2}||{\varphi}_{fh}- {\varphi}_{f}^{h}||_{1,{\Omega}_{p}}. \end{array} $$

(3.39)

Therefore, by combining all the above estimates, we get

$$ \begin{array}{@{}rcl@{}} \!\!\!\!\!\!\!||{\varphi}_{fh}- {\varphi}_{f}^{h}||^{2}_{1,{\Omega}_{p}}\!\leq\! c a_{f}({\varphi}_{fh}- {\varphi}^{h}_{f}, {\varphi}_{fh}- {\varphi}_{f}^{h}) \!\leq \!c H^{2} ||{\varphi}_{fh}- {\varphi}_{f}^{h}||_{1,{\Omega}_{p}}. \end{array} $$

(3.40)

Similarly, plugging $\textbf {v}_{h}=(0,{\varphi }_{mh}- {\varphi }_{m}^{h},0)$ into the equation (3.31) yields

$$ \begin{array}{@{}rcl@{}} a_{m}({\varphi}_{mh}- {\varphi}_{m}^{h}, {\varphi}_{mh}- {\varphi}_{m}^{h})&=&\frac{\sigma k_{m}}{\mu}(\varphi_{fh}-\varphi_{fH},{\varphi}_{mh}- {\varphi}_{m}^{h})\\ & \leq& c ||\varphi_{fh}-\varphi_{fH}||_{0,{\Omega}_{p}}||{\varphi}_{mh}- {\varphi}_{m}^{h}||_{0,{\Omega}_{p}}\\ &\leq& cH^{2}||{\varphi}_{mh}- {\varphi}_{m}^{h}||_{1,{\Omega}_{p}}. \end{array} $$

(3.41)

The combination of above two estimates (3.40)–(3.41) provides exactly the desired convergence analysis (3.29) for the dual-permeable region.

On the other hand, to derive the optimal error estimates for the velocity and pressure in the conduit region, the following auxiliary problem is introduced in the microfracture and matrix region: for any given $\vec {v}_{h}\in H_{c,h}$, find ${\Phi } \in H^{1}({\Omega }_{p})$ satisfying

$$ \begin{array}{@{}rcl@{}} -\nabla \cdot \left( \frac{k_{f}}{\mu}\nabla {\Phi} \right) &=&0\quad \mathrm{ in} {\Omega}_{p}, \end{array} $$

(3.42)

$$ \begin{array}{@{}rcl@{}} \frac{k_{f}}{\mu} \nabla {\Phi}\cdot \hat{n}_{p}&=& \frac{1}{\rho} \vec{v}_{h}\cdot \hat{n}_{p} \quad \text{on} {\Gamma}, \end{array} $$

(3.43)

$$ \begin{array}{@{}rcl@{}} \frac{k_{f}}{\mu} \nabla {\Phi}\cdot \hat{n}_{p} &=& 0 \quad \text{on} \partial {\Omega}_{p}\setminus {\Gamma}, \end{array} $$

(3.44)

which yields

$$ \begin{array}{@{}rcl@{}} ||(\frac{k_{f}}{\mu})^{1/2}\nabla {\Phi}||_{0,{\Omega}_{p}}\leq c ||\vec{v}_{h}||_{1,{\Omega}_{c}}. \end{array} $$

Since Γ is smooth, for any $\vec {v}_{h}\in H_{c,h}$, we can achieve

$$ \begin{array}{@{}rcl@{}} || {\Phi}||_{2,{\Omega}_{p}}\leq c ||\vec{v}_{h}||_{1,{\Omega}_{c}}. \end{array} $$

Plugging $\textbf {v}_{h}=(\vec {v}_{h},0,0)$ into the equations (3.31) and (3.32), to obtain

$$ \begin{array}{@{}rcl@{}} a_{c}(\vec{u}_{h}-{\vec{u}}^{h},\vec{v}_{h})+b(\vec{v}_{h},p_{h}- {p}^{h}) &= &{\int}_{\Gamma} \frac{1}{\rho}({\varphi}_{fh}-{\varphi}_{fH} )\vec{v}_{h}\cdot \hat{n}_{c} ds, \end{array} $$

(3.45)

$$ \begin{array}{@{}rcl@{}} b(\vec{u}_{h}-{\vec{u}}^{h},q_{h})&=&0. \end{array} $$

(3.46)

The right-hand side of (3.45) can be stated equivalently as:

$$ \begin{array}{@{}rcl@{}} && \frac{1}{\rho} {\int}_{\Gamma} ({\varphi}_{fh}-{\varphi}_{fH} )\vec{v}_{h}\cdot \hat{n}_{c} ds\\ &=&-{\int}_{\Gamma} ({\varphi}_{fh}-{\varphi}_{fH} )\frac{k_{f}}{\mu}\nabla {\Phi}\cdot \hat{n}_{p} ds \\ &=&-{\int}_{\partial {\Omega}_{p}}({\varphi}_{fh}-{\varphi}_{fH} )\frac{k_{f}}{\mu}\nabla {\Phi}\cdot \hat{n}_{p} ds\\ &=&-{\int}_{{\Omega}_{p}} ({\varphi}_{fh}-{\varphi}_{fH} )\nabla\cdot(\frac{k_{f}}{\mu}\nabla {\Phi})dx-{\int}_{{\Omega}_{p}}\frac{k_{f}}{\mu}\nabla({\varphi}_{fh}-{\varphi}_{fH})\cdot\nabla {\Phi} dx\\ &=&-{\int}_{{\Omega}_{p}}\frac{k_{f}}{\mu}\nabla({\varphi}_{fh}-{\varphi}_{fH} )\cdot\nabla {\Phi} dx \\ &=&- a_{f}({\varphi}_{fh}-{\varphi}^{h}_{f}, {\Phi})- a_{f}({\varphi}^{h}_{f}-{\varphi}_{fH}, {\Phi})\\&&+{\int}_{{\Omega}_{p}}\frac{\sigma k_{m}}{\mu} ({\varphi}_{fh}-{\varphi}_{fH} )\cdot {\Phi} dx. \end{array} $$

(3.47)

By using (3.29), the right-hand side of the equation (3.47) can be estimated as:

$$ \begin{array}{@{}rcl@{}} |- a_{f}({\varphi}_{fh}-{\varphi}^{h}_{f}, {\Phi})|&\leq& c || {\varphi}_{fh}-{\varphi}_{f}^{h}||_{1,{\Omega}_{p}}||\left( \frac{k_{f}}{\mu}\right)^{1/2}\nabla {\Phi}||_{0,{\Omega}_{p}}\\&\leq& c H^{2}||\vec{v}_{h}||_{1,{\Omega}_{c}}. \end{array} $$

(3.48)

It is obvious that

$$ \begin{array}{@{}rcl@{}} a_{f}({\varphi}_{f}^{h}-{\varphi}_{fH}, \psi_{fH})&=&0\ \ \ \forall \psi_{H}\in H_{p,H}. \end{array} $$

Suppose that Φ_fH ∈ H_p,H be the linear interpolation of Φ, then,

$$ \begin{array}{@{}rcl@{}} |a_{f}({\varphi}_{f}^{h}-{\varphi}_{fH},{\Phi})|&=&|a_{f}({\varphi}_{f}^{h}-{\varphi}_{fH},{\Phi}- {\Phi}_{fH})|\\ &\leq&c || {\varphi}_{f}^{h}-{\varphi}_{fH}||_{1,{\Omega}_{p}}||{\Phi}- {\Phi}_{fH}||_{1,{\Omega}_{p}}\\ &\leq&c H\left( || {\varphi}^{h}_{f}-{\varphi}_{fh}||_{1,{\Omega}_{p}} +|| {\varphi}_{fh}-{\varphi}_{fH}||_{1,{\Omega}_{p}} \right)||{\Phi}||_{2,{\Omega}_{p}}\\ &\leq&c H^{2}||\vec{v}_{h}||_{1,{\Omega}_{c}}. \end{array} $$

(3.49)

The last term of (3.47) can be controlled as

$$ \begin{array}{@{}rcl@{}} {\int}_{{\Omega}_{p}}\frac{\sigma k_{m}}{\mu} ({\varphi}_{fh}-{\varphi}_{fH} )\cdot {\Phi} dx & \leq & \frac{\sigma k_{m}}{\mu} ||{\varphi}_{fh}-{\varphi}_{fH} ||_{0,{\Omega}_{p}} ||{\Phi}||_{0,{\Omega}_{p}} \\ & \leq & cH^{2} || \varphi_{f} ||_{2,{\Omega}_{p}} || \left( \frac{k_{f}}{\mu}\right)^{\frac{1}{2}}\nabla {\Phi}||_{0,{\Omega}_{p}} \\ & \leq & c H^{2} ||\vec{v}_{h}||_{1,{\Omega}_{c}}. \end{array} $$

(3.50)

Then, finally, we summarize to obtain

$$ \begin{array}{@{}rcl@{}} | \frac{1}{\rho}{\int}_{\Gamma} ({\varphi}_{fh}-{\varphi}_{fH} )\vec{v}_{h}\cdot \hat{n}_{c} ds|\leq c H^{2}||\vec{v}_{h}||_{1,{\Omega}_{c}}. \end{array} $$

(3.51)

Thus,

$$ \begin{array}{@{}rcl@{}} ||\vec{u}_{h}- {\vec{u}}^{h}||^{2}_{1,{\Omega}_{c}}\leq c a_{c}(\vec{u}_{h}- {\vec{u}}^{h},\vec{u}_{h}- {\vec{u}}^{h})&\leq& | \frac{c}{\rho}{\int}_{\Gamma} ({\varphi}_{fh}-{\varphi}_{fH} )(\vec{u}_{h}- {\vec{u}}^{h})\cdot \hat{n}_{c} ds | \\ &\leq& c H^{2}||\vec{u}_{h}- {\vec{u}}^{h}||_{1,{\Omega}_{c}}. \end{array} $$

(3.52)

By the inf-sup condition, we can have

$$ \begin{array}{@{}rcl@{}} &&||p_{h}-p^{h}||_{0,{\Omega}_{c}}\\ &\leq& c {\sup_{0\neq \vec{v}_{h}\in H_{c,h}}}\frac{b(\vec{v}_{h}, p_{h}-{p}^{h}) }{||\vec{v}_{h}||_{1,{\Omega}_{c}}}\\ &\leq& c {\sup_{0\neq \vec{v}_{h}\in H_{c,h}}}\frac{|a_{c}(\vec{u}_{h}- {\vec{u}}^{h},\vec{v}_{h}) |+|\frac{1}{\rho }{\int}_{\Gamma} ({\varphi}_{fh}-{\varphi}_{fH} )\vec{v}_{h}\cdot \hat{n}_{c} ds |}{||\vec{v}_{h}||_{1,{\Omega}_{c}}} \\&\leq& c H^{2}. \end{array} $$

Hence, the error estimate (3.30) is also proved. □

By using the triangle inequality and Theorem 3.3, it is easy to obtain the following corollary.

Corollary 3.1

Let $(\vec {u}^{h},p^{h}, {\varphi }^{h}_{f},{\varphi ^{h}_{m}})$ be the solution of Algorithm 2, we have the following optimal error estimates

$$ \begin{array}{@{}rcl@{}} ||\varphi-{\varphi^{h}_{f}}||_{1,{\Omega}_{p}}+||\varphi-{\varphi^{h}_{m}}||_{1,{\Omega}_{p}}&\leq c (h+H^{2}), \end{array} $$

(3.53)

$$ \begin{array}{@{}rcl@{}} ||\vec{u}-\vec{u}^{h}||_{1,{\Omega}_{c}}+||p-p^{h}||_{0,{\Omega}_{c}}&\leq c (h+H^{2}).\end{array} $$

(3.54)

Specifically, when choosing H = O(h^1/2), we have

$$ \begin{array}{@{}rcl@{}} ||\varphi-{\varphi^{h}_{f}}||_{1,{\Omega}_{p}}+||\varphi-{\varphi^{h}_{m}}||_{1,{\Omega}_{p}}&\leq c h, \end{array} $$

(3.55)

$$ \begin{array}{@{}rcl@{}} ||\vec{u}-\vec{u}^{h}||_{1,{\Omega}_{c}}+||p-p^{h}||_{0,{\Omega}_{c}}&\leq c h.\end{array} $$

(3.56)

4 Numerical experiments

In this section, four numerical examples are presented to validate the proposed two-grid method and illustrate the feature of the dual-permeability-Stokes multiphysics interface system. In the first numerical test, the optimal convergence order is obtained for an analytical solution. In the second example, we test accuracy for a smaller value of the intrinsic permeability with relative error. In the third example, the flow speed and streamlines are illustrated on a horizontal open-hole with production wellbore. The fourth experiment demonstrates the lid-driven cavity flow. To compute the Stokes problem, MINI element pair (P_1b,P₁) is used. In the porous medium, P₁ Lagrangian finite elements are used to compute the matrix and microfracture flow pressure. On the other hand, we also utilize Hood-Taylor element (P₂,P₁) for the Stokes velocity and pressure, and quadratic element P₂ is used for the microfracture and matrix pressure. Moreover, the relation between the coarse mesh H and the fine mesh h is chosen as h = H².

For simplicity, the coupled algorithm is denoted by SFEM, and the two-grid algorithm by TGM. The numerical experiments are conducted on an ASUS X555LF-XO040D laptop with 8 GB RAM and Core i5 configuration. On the other hand, we utilize open source FreeFem++ software to conduct and implement the numerical experiments [90].

4.1 Analytical solution test: 1

In the first numerical test, the physical parameters ρ, ν, α, μ, k_m, k_f are simply taken as 1.0. The computational domains are defined as Ω_c = (0,1) × (1,2) and Ω_p = (0,1) × (0,1) with interface Γ = (0,1) ×{1}.

The below analytical solution satisfies the Beavers-Joseph-Saffman interface condition

$$ \begin{array}{@{}rcl@{}} \vec{u}&=& \left( x^{2} (y - 1)^{2} + y, - \frac{2}{3}x(y - 1)^{3} + 2 - \pi \sin (\pi x)\right),\\ p &=& \left( 2 - \pi \sin (\pi x)\right)\sin (\frac{\pi }{2}y),\\ \varphi_{f} &=& \left( 2 - \pi \sin (\pi x)\right)\left( 1 - y - \cos (\pi y)\right), \\ \varphi_{m} &=& (2-\pi sin({\pi x}))cos(\pi(1- y)). \end{array} $$

The force term and the boundary condition are determined by this analytical solution.

In Tables 1 and 2, the error obtained comparing the exact solution and approximate solution for SFEM and TGM, respectively by utilizing P_1b − P₁ − P₁ − P₁ finite elements. Table 1 shows that microfracture and matrix pressure H¹-norm, Stokes velocity H¹-norm, and pressure L²-norm obtain O(h) order convergence accuracy. On the other hand, Table 1 shows that one-level method consumes more CPU time. In Table 2, the TGM approximate accuracy is illustrated by choosing h = H² which shows that $\nabla \varphi _{f}, \nabla \varphi _{m}, \nabla \vec {u}$ and p in the L²-norm achieve optimal convergence order. As expected, TGM consumes less CPU time than SFEM. Furthermore, we present the approximate accuracy by using P₂ − P₁ − P₂ − P₂ finite elements in Table 3 and achieve almost second order accuracy in Stokes velocity, microfracture and matrix pressure H¹-norm and Stokes pressure L²-norm, respectively.

Table 1 The approximate accuracy and CPU performance for P_1b − P₁ − P₁ − P₁ finite elements by SFEM

Table 2 The approximate accuracy and CPU performance for P_1b − P₁ − P₁ − P₁ finite elements by TGM

Table 3 The approximate accuracy and CPU performance for P₂ − P₁ − P₂ − P₂ finite elements by TGM

4.2 Analytical solution test: 2

In the second numerical test, we choose the smaller value for the microfracture and matrix intrinsic permeability k_f = 0.1 and k_m = 0.001, respectively. Moreover, other constants ρ, ν,α,μ are simply chosen to be 1.

The following exact solution satisfies the Beavers-Joseph-Saffman interface condition

$$ \begin{array}{@{}rcl@{}} \vec{u}&=& \left( (y-1)^{2},x(x-1)\right),\\ p &=& \left[2\nu(x+y-1)+\frac{1}{3 k_{f}}\right],\\ \varphi_{f} &=& \left[\frac{1}{k_{f}}\left( x(1-x)(y-1)+\frac{1}{3}y^{3}-y^{2}+y\right)+ 2\nu x\right],\\ \varphi_{m} &=& \left[\frac{1}{k_{m}}\left( x^{2}(1-x^{2})(y^{2}-2y)+\frac{1}{2}y^{4}-y^{3}+\frac{1}{2}y^{2}\right)-2\nu x\right]. \end{array} $$

The force term and boundary conditions are determined by the exact solution. To perform this numerical test, we utilize P_1b − P₁ − P₁ − P₁ finite elements.

In Table 4, the approximate accuracy for the relative error is listed for TGM by choosing microfracture intrinsic permeability k_f = 0.1 and matrix intrinsic permeability k_m = 0.001. Table 4 shows that we achieve first-order convergence accuracy for the microfracture pressure, matrix pressure, Stokes velocity, and Stokes pressure, respectively.

Table 4 The approximate accuracy by TGM for the intrinsic permeability k_f = 0.1 and k_m = 0.001

4.3 Horizontal wellbore with open-hole completion

In this experiment, the flow speed, magnitudes, streamlines and distribution of pressure are illustrated in a horizontal production wellbore with open-hole completion. The horizontal open-hole with vertical production wellbore has enormous applications in the hydrocarbon extraction process, and many other areas of the naturally fractured reservoirs [23, 24, 34, 37,38,39, 41, 42].

To perform the simulation of the horizontal wellbore with open-hole completion [23, 37,38,39], the geometrical shape is considered as shown in Fig. 2 [23]. The dual-porous domain is taken as Ω_p = [0,2]² where the horizontal wellbore with open-hole completion lies in between the square domain which is assumed as Ω_c = [0.6,1.4] × [0.9,1.1]. The fluid flow from the microfracture to the conduit passes through the interface Γ_cp satisfying four interface conditions described in the equations (2.8)–(2.11).

Fig. 2

The computational domain for horizontal wellbore with open-hole completion consists of conduit domain Ω_c and dual-permeability domain Ω_p

The boundary conditions of the current experiment are imposed in the following way. On outside of the outflow boundary Γ_out, no-direct communication condition is imposed between the matrix and fracture pressure which implies to $-\frac {k_{m}}{\mu }\nabla \varphi _{m}\cdot \hat {n}_{p}=0$ and $-\frac {k_{f}}{\mu }\nabla \varphi _{f}\cdot \hat {n}_{p}=0$. On the inside of the outflow boundary Γ_out, homogeneous Neumann boundary condition $(-p \mathbf {I}+\nu \nabla \vec {u}) \cdot \hat {n}_{c}=0$ is applied for free outflow. The vertical wellbore, known as production well is connected with the horizontal well on the boundary Γ_out, where the fluid flow can pass out through it.

The parameters value of the model are considered as intrinsic permeability k_f = 2.5 × 10^− 1, k_m = 10^− 9, dynamic viscosity μ = 2.5 × 10^− 3, kinematic viscosity ν = 5.0 × 10^− 2, density ρ = 5.0 × 10^− 2, constant parameter α = 2.5 and shape factor σ = 0.25. The microfracture pressure on the boundary of the dual-permeability medium is considered as φ_f = 5 × 10¹ and the matrix pressure φ_m = 10⁴. The mesh size is uniform in the domain and chosen as h_max = 0.03.

The fundamental properties of the naturally fractured reservoir consisting of the dual-porosity/permeability medium state that, the matrix block serves as the main storage of the fluid while the microfracture region is fed by the matrix region. The horizontal wellbore is fed by the microfracture, which shows that fluid flow and mass exchange between this medium is sequential. Moreover, the fluid flow of the matrix region does not directly communicate with the horizontal wellbore. Figure 3 (left) demonstrates the flow between microfracture and horizontal wellbore. The fluid flows from the matrix to microfracture and then microfracture to the horizontal wellbore. As expected, the faster flow is located in the horizontal wellbore, where the production well is attached. The pattern of the streamlines also indicate that the fluid is flowing from the microfracture to the horizontal open-hole towards the production wellbore. Figure 3 (right) represents the fluid flow and streamlines in the matrix region. In Fig. 4, the distribution of pressure is illustrated in the microfracture and matrix region, respectively, which appear reasonable. It is worthwhile noting that Figs. 3 and 4 are generated by using P_1b − P₁ − P₁ − P₁ finite elements.

Fig. 3

The flow speed and streamlines around a horizontal wellbore with open-hole completion for σ = 0.25, k_f = 2.5 × 10^− 1, and k_m = 10^− 9 by using P_1b − P₁ − P₁ − P₁ finite elements. Left: the flow in the microfracture and the horizontal wellbore; right: the flow in the matrix region

Fig. 4

The distribution of pressure around a horizontal wellbore with open-hole completion for σ = 0.25, k_f = 2.5 × 10^− 1, and k_m = 10^− 9 by using P_1b − P₁ − P₁ − P₁ finite elements. Left: the pressure in the microfracture region; right: the pressure in the matrix region

In Fig. 5, we demonstrate magnitudes, contour and streamlines around a horizontal wellbore for the comparison purpose by using P₂ − P₁ − P₂ − P₂ finite elements which appear similar as Fig. 3. The rest of the numerical simulations in this example are conducted through P_1b − P₁ − P₁ − P₁ finite elements.

Fig. 5

The flow speed and streamlines around a horizontal wellbore with open-hole completion for σ = 0.25, k_f = 2.5 × 10^− 1, and k_m = 10^− 9 by using P₂ − P₁ − P₂ − P₂ finite elements. Left: the flow in the microfracture and the horizontal wellbore; right: the flow in the matrix region

In Fig. 6, the impact of the larger value of permeability is presented on the matrix region by gradually increasing the permeability k_m = 10^− 8 and k_m = 10^− 7, respectively. As expected, the increase of the permeability produces faster flow speed in the matrix region, which can be seen in the contour color bar.

Fig. 6

The flow speed and streamlines in the matrix region for σ = 0.25, and k_f = 2.5 × 10^− 1 by using P_1b − P₁ − P₁ − P₁ finite elements. Left: k_m = 10^− 8; right: k_m = 10^− 7

In naturally fractured reservoir engineering, shape factor σ plays an essential role in the matrix-fracture transfer function. The rate of mass transfer from the matrix to the fracture is directly proportional to the shape factor [31, 32]. The value of shape factor generally varies from 0 to 1, where the larger value of the shape factor generates faster flow, and the smaller value produces slower flow. Figure 7 illustrates the flow rate of the matrix region for the parameter value σ = 0.009 and σ = 0.1, respectively. From the figures, one can obviously observe that the smaller value of the shape factor generates slower flow and larger value produces faster fluid flow. The above numerical results illustrate the complicated flow characteristics and exclusive feature around the horizontal wellbore with open-hole completion.

Fig. 7

The flow speed and streamlines in the matrix region for k_f = 2.5 × 10^− 1, k_m = 10^− 9 and by using P_1b − P₁ − P₁ − P₁ finite elements. Left: σ = 0.009; right: σ = 0.1

4.4 Modified lid-driven cavity flow

In this example, the lid-driven cavity flow is considered to illustrate the streamlines and pressure lines through P_1b − P₁ − P₁ − P₁ finite elements. The computational domain is considered similar as [69, 89]. The Stokes and microfracture-matrix fluid flow subdomains are assumed as Ω_c = (0,1) × (1,1.25) and Ω_p = (0,1) × (0,1), respectively with the interface Γ = (0,1) ×{1}. On the interface Γ between conduit and porous medium, four interface conditions (2.8)–(2.11) are utilized.

A modified driven cavity flow with the Dirichlet boundary conditions for the flow region is used,

$$ \begin{array}{@{}rcl@{}} \vec{u}:&=& [sin(\pi x), 0]{\kern18pt}\text{on} (0,1)\times \lbrace 1.25 \rbrace, \\ \vec{u}:&=& (0,0){\kern46pt}\text{on} \lbrace 0,1\rbrace \times (1,1.25). \end{array} $$

In the dual-porosity region, homogeneous Dirichlet boundary conditions are imposed on the left, right and bottom wall for the microfracture and matrix pressure φ_f = 0 and φ_m = 0, respectively.

The value of the parameters ν, α, ρ, and μ are simply taken as 1.0. The intrinsic permeability k_f and k_m are considered as 1.0. The body force $\vec {f}$ and q_p are assumed as 0. The mesh size is taken as h = 1/256.

In Figs. 8 and 9, the streamlines, flow speed, and contour lines are illustrated for the comparison purpose with the proposed TGM by considering all the parameters 1.0 which are similar to [89]. On the other hand, we show the lid-driven cavity flow for the smaller intrinsic permeability by choosing microfracture permeability k_f = 0.01 and matrix permeability k_m = 10^− 8 in Figs. 10 and 11 where streamlines and contour demonstrate similar flow behavior. As expected, the flow speed decreases due to the smaller value of the microfracture and matrix permeability.

Fig. 8

The flow speed and streamlines for k_f = 1.0, k_m = 1.0 and σ = 0.5. Left: conduit and microfracture region; right: matrix region

Fig. 9

The pressure lines for k_f = 1.0, k_m = 1.0 and σ = 0.5. Left: conduit and microfracture region; right: matrix region

Fig. 10

The flow speed and streamlines for k_f = 10^− 2, k_m = 10^− 8 and σ = 0.5. Left: conduit and microfracture region; right: matrix region

Fig. 11

The pressure lines for k_f = 10^− 2, k_m = 10^− 8 and σ = 0.5. Left: conduit and microfracture region; right: matrix region

Figure 12 illustrates the gradually decreasing the matrix intrinsic permeability from k_m = 10^− 6 to 10^− 10. As expected, the decrease of matrix intrinsic permeability produce slower flow speed which can be seen in the legend bar.

Fig. 12

The flow speed and streamlines for matrix region with k_f = 10^− 2 and σ = 0.1. Left: k_m = 10^− 6; right: k_m = 10^− 10

5 Conclusion and future work

In this contribution, a two-grid finite element discretization for the dual-permeability-Stokes fluid flow model is presented. In the first step, the approximate solution on the coarse grid is generated, while the results of the coarse grid are used to derive the solution on the fine grid in the second step. On the fine mesh, the global problem is decoupled into three parallel subproblems. The weak formulation is presented, and the optimal error estimate is derived for the proposed two-grid method. Numerical tests illustrate that the proposed method is stable and efficient. In the future, this method can be extended for the lowest-equal-order finite element method P₁ − P₁ − P₁ − P₁. The lowest-equal-order finite elements do not satisfy the benchmark inf-sup condition, which produces oscillation need to be restored by considering the stabilization term [69, 89]. On the other hand, two-grid method can be applied to study the time-dependent coupled problems where the main difficulty arises with the relationship between the time step size and the mesh refinement [91,92,93,94]. Furthermore, two-grid method will be applied for the nonlinear cases to investigate the dual-permeability-Navier-Stokes model [68, 75, 76]. The nonlinearity can cause enormous difficulty in handling the interface conditions as well as the error bounds. Besides, the current two-grid method can be improved by decoupling the coupled algorithm into several parallel subproblems to generate the coarse grid solution, which can significantly reduce the computational cost.