Skip to main content
SpringerLink
Log in

Extrapolated sequential constraint method for variational inequality over the intersection of fixed-point sets

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

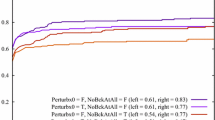
This paper deals with the solving of variational inequality problem where the constrained set is given as the intersection of a number of fixed-point sets. To this end, we present an extrapolated sequential constraint method. At each iteration, the proposed method is updated based on the ideas of a hybrid conjugate gradient method used to accelerate the well-known hybrid steepest descent method, and an extrapolated cyclic cutter method for solving a common fixed-point problem. We prove strong convergence of the method under some suitable assumptions of step-size sequences. We finally show the numerical efficiency of the proposed method compared to some existing methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Aoyama, K., Kohsaka, F.: Viscosity approximation process for a sequence of quasi-nonexpansive mappings. Fixed Point Theory Appl. 17. https://doi.org/10.1186/1687-1812-2014-17 (2014)

  2. Bauschke, H.H., Combettes, P.L.: A weak-to-strong convergence principle for Fejér-monotone methods in Hilbert spaces. Math. Oper. Res. 26, 248–264 (2001)

    Article  MathSciNet  Google Scholar 

  3. Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces (2nd ed.) CMS Books in Mathematics. Springer, New York (2017)

    Book  Google Scholar 

  4. Bregman, L.M.: Finding the common point of convex sets by the method of successive projection. Dokl. Akad. Nauk SSSR 162(3), 487–490 (1965)

    MathSciNet  Google Scholar 

  5. Cegielski, A.: Generalized relaxations of nonexpansive operators and convex feasibility problems. Contemp. Math. 513, 111–123 (2010)

    Article  MathSciNet  Google Scholar 

  6. Cegielski, A.: Iterative Methods for Fixed Point Problems in Hilbert Spaces. Lecture Notes in Mathematics 2057. Springer, Berlin (2012)

    Google Scholar 

  7. Cegielski, A.: Application of quasi-nonexpansive operators to an iterative method for variational inequality. SIAM. J. Optim. 25(4), 2165–2181 (2015)

    Article  MathSciNet  Google Scholar 

  8. Cegielski, A., Censor, Y.: Opial-type theorems and the common fixed point problem. In: Bauschke, H., Burachik, R., Combettes, P., Elser, V., Luke, D., Wolkowicz, H (eds.) Fixed-Point Algorithms for Inverse Problems in Science and Engineering. Springer Optimization and Its Applications, vol. 49. Springer, New York (2011)

  9. Cegielski, A., Censor, Y.: Extrapolation and local acceleration of an iterative process for common fixed point problems. J. Math. Anal. Appl. 394, 809–818 (2012)

    Article  MathSciNet  Google Scholar 

  10. Cegielski, A., Nimana, N.: Extrapolated cyclic subgradient projection methods for the convex feasibility problems and their numerical behaviour. Optimization 68, 145–161 (2019)

    Article  MathSciNet  Google Scholar 

  11. Cegielski, A., Zalas, R.: Methods for variational inequality problem over the intersection of fixed point sets of quasi-nonexpansive operators. Numer. Funct. Anal. Optim. 34, 255–283 (2013)

    Article  MathSciNet  Google Scholar 

  12. Dai, Y.H., Yuan, Y.: A nonlinear conjugate gradient method with a strong global convergence property. SIAM J. Optim. 10, 177–182 (1999)

    Article  MathSciNet  Google Scholar 

  13. Facchinei, F., Pang, J. -S.: Finite-Dimensional Variational Inequalities and Complementarity Problems, vol. I. Springer, New York (2003)

    MATH  Google Scholar 

  14. Fletcher, R., Reeves, C.M.: Function minimization by conjugate gradients. Comput. J. 7, 149–154 (1964)

    Article  MathSciNet  Google Scholar 

  15. Gibali, A., Reich, S., Zalas, R.: Outer approximation methods for solving variational inequalities in Hilbert space. Optimization 66, 417–437 (2017)

    Article  MathSciNet  Google Scholar 

  16. Gilbert, J.C., Nocedal, J.: Global convergence properties of conjugate gradient methods for optimization. SIAM J. Optim. 2, 21–42 (1992)

    Article  MathSciNet  Google Scholar 

  17. Goldstein, A.A.: Convex programming in Hilbert space. Bull. Am. Math. Soc. 70, 709–710 (1964)

    Article  MathSciNet  Google Scholar 

  18. Iiduka, H.: Three-term conjugate gradient method for the convex optimization problem over the fixed point set of a nonexpansive mapping. Appl. Math. Comput. 217, 6315–6327 (2011)

    MathSciNet  MATH  Google Scholar 

  19. Iiduka, H.: Fixed point optimization algorithms for distributed optimization in networked systems. SIAM J. Optim. 23, 1–26 (2013)

    Article  MathSciNet  Google Scholar 

  20. Iiduka, H.: Convex optimization over fixed point sets of quasi-nonexpansive and nonexpansive mappings in utility-based bandwidth allocation problems with operational constraints. J. Comput. Appl. Math. 282, 225–236 (2015)

    Article  MathSciNet  Google Scholar 

  21. Iiduka, H.: Acceleration method for convex optimization over the fixed point set of a nonexpansive mapping. Math. Program. 149, 131–165 (2015)

    Article  MathSciNet  Google Scholar 

  22. Iiduka, H.: Distributed optimization for network resource allocation with nonsmooth utility functions. IEEE Trans. Control. Netw. Syst. 6, 1354–1365 (2019)

    Article  MathSciNet  Google Scholar 

  23. Iiduka, H.: Stochastic fixed point optimization algorithm for classifier ensemble. IEEE Trans Cybern. 50, 4370–4380 (2020)

    Article  Google Scholar 

  24. Iiduka, H., Hishinuma, K.: Acceleration method combining broadcast and incremental distributed optimization algorithms. SIAM J. Optim. 24, 840–1863 (2014)

    Article  MathSciNet  Google Scholar 

  25. Iiduka, H., Yamada, I.: A use of conjugate gradient direction for the convex optimization problem over the fixed point set of a nonexpansive mapping. SIAM J. Optim. 19, 1881–1893 (2009)

    Article  MathSciNet  Google Scholar 

  26. Kaczmarz, S.: Angenäherte Auflösung von Systemen linearer Gleichungen. Bull. Int. A35, 355–357 (1937). English translation: Kaczmarz, S.: Approximate solution of systems of linear equations. Int. J. Contr. 57, 1269–1271 (1993)

    MATH  Google Scholar 

  27. Liu, C.: An acceleration scheme for row projection methods. J. Comput. Appl. 57, 363–391 (1995)

    Article  MathSciNet  Google Scholar 

  28. Maingé, P.E.: Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization. Set-Valued Anal. 16, 899–912 (2008)

    Article  MathSciNet  Google Scholar 

  29. Nimana, N., Petrot, N., Prangprakhon, M.: A centralized three-term conjugate gradient method for variational inequality problem over the common fixed point constraints (submitted)

  30. Nocedal, J., Wright, S.J.: Numerical Optimization. Springer, Springer Series in Operations Research and Financial Engineering, Berlin (1999)

    Book  Google Scholar 

  31. Opial, Z.: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Am. Math. Soc. 73, 591–597 (1967)

    Article  MathSciNet  Google Scholar 

  32. Prangprakhon, M., Nimana, N., Petrot, N.: A sequential constraint method for solving variational inequality over the intersection of fixed point sets. Thai J. Math. 18(3), 1105–1123 (2020)

    MathSciNet  Google Scholar 

  33. Xu, H.K.: Iterative algorithm for nonlinear operators. J. London Math. Soc. 66, 240–256 (2002)

    Article  MathSciNet  Google Scholar 

  34. Yamada, I.: The hybrid steepest descent method for the variational inequality problem over the intersection of fixed point sets of nonexpansive mappings. In: Butnariu, D., Censor, Y., Reich, S (eds.) Inherently Parallel Algorithms in Feasibility and Optimization and their Applications, pp. 473–504. Elsevier, Amsterdam (2001)

  35. Zarantonello, E.H.: Projections on convex sets in Hilbert space and spectral theory. In: Zarantonello, E. H. (ed.) Contributions to Nonlinear Functional Analysis, pp. 237–424. Academic Press, New York (1971)

  36. Zhang, L., Zhou, W., Li, D.H.: A descent modified polak-ribiere-polyak conjugate gradient method and its global convergence. IMA J. Numer. Anal. 26, 629–640 (2006)

    Article  MathSciNet  Google Scholar 

  37. Zhang, L., Zhou, W., Li, D.H.: Global convergence of a modified fletcher-reeves conjugate gradient method with Armijo-type line search. Numer. Math. 104, 561–572 (2006)

    Article  MathSciNet  Google Scholar 

  38. Zhang, L., Zhou, W., Li, D.H.: Some descent three-term conjugate gradient methods and their global convergence. Optim. Methods Softw. 22, 697–711 (2007)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors are thankful to the Editor and two anonymous referees for comments and remarks which improved the quality and presentation of the paper. Mootta Prangprakhon was partially supported by Science Achievement Scholarship of Thailand (SAST), and Faculty of Science, Khon Kaen University. Nimit Nimana was partially supported by Thailand Science Research and Innovation under the project IRN62W0007.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen, 40002, Thailand

    Mootta Prangprakhon & Nimit Nimana

Authors
  1. Mootta Prangprakhon
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nimit Nimana
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nimit Nimana.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Prangprakhon, M., Nimana, N. Extrapolated sequential constraint method for variational inequality over the intersection of fixed-point sets. Numer Algor 88, 1051–1075 (2021). https://doi.org/10.1007/s11075-021-01067-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-021-01067-z

Keywords

Search

Navigation