Skip to main content
SpringerLink
Log in

A filter method with a priori and a posteriori parameter choice for the regularization of Cauchy problems for biharmonic equations

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

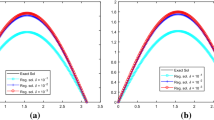
In the present paper, we devote our effort to Cauchy boundary value problems for biharmonic equations. In general, the investigated problem is ill-posed. Therefore, we develop a filter method to defeat the ill-posedness of the problem. Explicit convergence rate is established under both a priori and a posteriori parameter choice rules. Finally, a numerical example is presented to illustrate the ill-posedness of the problem as well as the effectiveness of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Andersson, L. E., Elfving, T., Golub, G. H.: Solution of biharmonic equations with application to radar imaging. J. Comput. Appl. Math. 94(2), 153–180 (1998)

    Article  MathSciNet  Google Scholar 

  2. Beck, J V, Blackwell, Ben, St Clair, Jr., C.R.: Inverse Heat Conduction Ill-posed Problems. A Wiley-Interscience, New York (1985)

    MATH  Google Scholar 

  3. Benrabah, A., Boussetila, N.: Modified nonlocal boundary value problem method for an ill-posed problem for the biharmonic equation. Inverse Probl. Sci. Eng., 1–29 (2018)

  4. Doan, V.N., Nguyen, H.T, Vo, A.K., Vo, V.A.: A note on the derivation of filter regularization operators for nonlinear evolution equations. Appl. Anal. 97 (1), 3–12 (2018)

    Article  MathSciNet  Google Scholar 

  5. Ehrlich, L. N., Gupta, M. M.: Some difference schemes for the biharmonic equation. SIAM J. Numer. Anal. 12(5), 773–790 (1975)

    Article  MathSciNet  Google Scholar 

  6. Eldén, L., Berntsson, F., Regińska, T.: Wavelet and Fourier methods for solving the sideways heat equation. SIAM J. Sci. Comput. 21(6), 2187–2205 (2000)

    Article  MathSciNet  Google Scholar 

  7. Engl, H.W., Hanke, M., Neubauer, A.: Regularization of inverse problems, vol. 375. Springer Science & Business Media (1996)

  8. Feng, X.-L., Eldén, L., Fu, C.-L.: A quasi-boundary-value method for the C,auchy problem for elliptic equations with nonhomogeneous Neumann data. J. Inverse Ill-Posed Probl. 18(6), 617–645 (2010)

    Article  MathSciNet  Google Scholar 

  9. Hào, D.N., Van Duc, N., Lesnic, D.: A non-local boundary value problem method for the Cauchy problem for elliptic equations. Inverse Probl. 25(5), 055002, 27 (2009)

    Article  MathSciNet  Google Scholar 

  10. Huy, T.N., Kirane, M., Le, L.D., Van Nguyen, T.: Filter regularization for an inverse parabolic problem in several variables. Electron. J Differential Equations, pages Paper 24, 13 (2016)

  11. Kal’menov, T., Iskakova, U.: On an ill-posed problem for a biharmonic equation. Filomat 31(4), 1051–1056 (2017)

    Article  MathSciNet  Google Scholar 

  12. Kal’menov, T.S., Sadybekov, M.A., Iskakova, U.A.: On a criterion for the solvability of one ill-posed problem for the biharmonic equation. J. Inverse Ill-Posed Probl. 24(6), 777–783 (2016)

    Article  MathSciNet  Google Scholar 

  13. Lai, M. C., Liu, H. C.: Fast direct solver for the biharmonic equation on a disk and its application to incompressible flows. Appl Math Comput. 164(3), 679–695 (2005)

    MathSciNet  MATH  Google Scholar 

  14. Landau, M. D., Lifshits, E. M.: Theory of Elasticity. Pergamon Press, Oxford (1986)

    Google Scholar 

  15. Hong, P.L., Minh, T.L., Quan, P.H.: On a three dimensional Cauchy problem for inhomogeneous Helmholtz equation associated with perturbed wave number. J. Comput. Appl. Math. 335, 86–98 (2018)

    Article  MathSciNet  Google Scholar 

  16. Qian, Z., Chu-Fu, L., Li, Z.-P.: Two regularization methods for a C,auchy problem for the Laplace equation. J. Math. Anal Appl. 338(1), 479–489 (2008)

    Article  MathSciNet  Google Scholar 

  17. Seidman, T.I.: Optimal filtering for the backward heat equation. SIAM J. Numer. Anal. 33(1), 162–170 (1996)

    Article  MathSciNet  Google Scholar 

  18. Selvadurai, A. P. S.: Partial Differential Equations in Mechanics 2: The biharmonic equation, Poisson’s equation. Springer Science and Business Media (2013)

  19. Timoshenko, S., Goodier, J. N.: Theory of Elasticity. McGraw-Hill, New York (1951)

  20. Zeb, A., Ingham, D. B., Lesnic, D.: The method of fundamental solutions for a biharmonic inverse boundary determination problem. Comput. Mech. 42(3), 371–379 (2008)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute for Computational Science and Technology, SBI building, Quang Trung Software City, Tan Chanh Hiep Ward, District 12, Ho Chi Minh City, Vietnam

    Tran Nhat Luan & Tran Thi Khieu

  2. Division of Computational Mathematics and Engineering, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam

    Tra Quoc Khanh

  3. Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam

    Tra Quoc Khanh

Authors
  1. Tran Nhat Luan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tran Thi Khieu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tra Quoc Khanh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tra Quoc Khanh.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Luan, T.N., Khieu, T.T. & Khanh, T.Q. A filter method with a priori and a posteriori parameter choice for the regularization of Cauchy problems for biharmonic equations. Numer Algor 86, 1721–1746 (2021). https://doi.org/10.1007/s11075-020-00951-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-020-00951-4

Keywords

Mathematics Subject Classification 2010

Search

Navigation