Skip to main content
SpringerLink
Log in

Identification of the time-dependent source term in a multi-term time-fractional diffusion equation

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

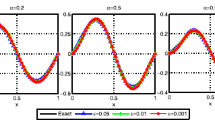
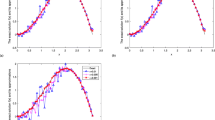
The multi-term time-fractional diffusion equation is a useful tool in the modeling of complex systems. This paper aims to identifying a time-dependent source term in a multi-term time-fractional diffusion equation from the boundary Cauchy data. The regularity of the weak solution for the direct problem with homogeneous Neumann boundary condition is proved. We provide the uniqueness and a stability estimate for the inverse time-dependent source problem. On the other hand, the inverse time-dependent source term is formulated into a variational problem by the Tikhonov regularization, with the help of sensitivity problem and adjoint problem we use a conjugate gradient method to find the approximate time-dependent source term. Numerical experiments for five examples in one-dimensional and two-dimensional cases show that our proposed method is effective and stable.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Adams, E.E., Gelhar, L.W.: Field-study of dispersion in a heterogeneous aquifer.2. spatial moments analysis. Water Resour. Res. 28(12), 3293–3307 (1992)

    Google Scholar 

  2. Berkowitz, B., Scher, H., Silliman, S.E.: Anomalous transport in laboratory-scale, heterogeneous porous media. Water Resour. Res. 36, 149–158 (2000)

    Google Scholar 

  3. Brezis, H.: Functional Analysis, Sobolev Spaces and Partial Differential Equations. Springer, New York (2011)

    MATH  Google Scholar 

  4. Caputo, M.: Mean fractional-order-derivatives differential equations and filters. Ann. Univ. Ferrara. 41, 73–84 (1995)

    MathSciNet  MATH  Google Scholar 

  5. Chechkin, A.V., Gorenflo, R., Sokolov, I.M., Gonchar, V.Y.: Distributed order time fractional diffusion equation. Fract. Calc. Appl. Anal. 6(3), 259–279 (2003)

    MathSciNet  MATH  Google Scholar 

  6. Coimbra, C.F.M.: Mechanics with variable-order differential operators. Ann. Phys. 12(11–12), 692–703 (2003)

    MathSciNet  MATH  Google Scholar 

  7. Courant, R., Hilbert, D.: Methods of Mathematical Physics, vol. I. Interscience Publishers, Inc., New York (1953)

    MATH  Google Scholar 

  8. Daftardar-Gejji, V., Bhalekar, S.: Boundary value problems for multi-term fractional differential equations. J. Math. Anal. Appl. 345(2), 754–765 (2008)

    MathSciNet  MATH  Google Scholar 

  9. Dehghan, M., Safarpoor, M., Abbaszadeh, M.: Two high-order numerical algorithms for solving the multi-term time fractional diffusion-wave equations. J. Comput. Appl. Math. 290, 174–195 (2015)

    MathSciNet  MATH  Google Scholar 

  10. Engl, H.W., Hanke, M., Neubauer, A.: Regularization of Inverse Problems, Mathematics and Its Applications, vol. 375. Kluwer Academic Publishers Group, Dordrecht (1996)

    MATH  Google Scholar 

  11. Giona, M., Cerbelli, S., Roman, H.E.: Fractional diffusion equation and relaxation in complex viscoelastic materials. Physica A 191(1-4), 449–453 (1992)

    Google Scholar 

  12. Hanke, M., Hansen, P.C.: Regularization methods for large-scale problems. Survey Math. Indust. 3(4), 253–315 (1993)

    MathSciNet  MATH  Google Scholar 

  13. Hasanov, A., DuChateau, P., Pektaş, B.: An adjoint problem approach and coarse-fine mesh method for identification of the diffusion coefficient in a linear parabolic equation. J. Inverse Ill-Posed Probl. 14(5), 435–463 (2006)

    MathSciNet  MATH  Google Scholar 

  14. Hatano, Y., Hatano, N.: Dispersive transport of ions in column experiments: an explanation of long-tailed profiles. Water Resour. Res. 34(5), 1027–1033 (1998)

    Google Scholar 

  15. Henry, B.I., Langlands, T.A.M., Wearne, S.L.: Fractional cable models for spiny neuronal dendrites. Phys. Rev. Lett. 100, 128103 (2008)

    Google Scholar 

  16. Jiang, H., Liu, F., Turner, I., Burrage, K.: Analytical solutions for the multi-term time-fractional diffusion-wave/diffusion equations in a finite domain. Comput. Math. Appl. 64(10), 3377–3388 (2012)

    MathSciNet  MATH  Google Scholar 

  17. Jin, B., Lazarov, R., Liu, Y., Zhou, Z.: The Galerkin finite element method for a multi-term time-fractional diffusion equation. J. Comput. Phys. 281, 825–843 (2015)

    MathSciNet  MATH  Google Scholar 

  18. Kilbas, A.A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations, vol. 204. Elsevier, Amsterdam (2006)

    MATH  Google Scholar 

  19. Li, G.S., Sun, C.L., Jia, X., Du, D.H.: Numerical solution to the multi-term time fractional diffusion equation in a finite domain. Numer. Math. Theory Methods Appl. 9(3), 337–357 (2016)

    MathSciNet  MATH  Google Scholar 

  20. Li, Z., Imanuvilov, O.Y., Yamamoto, M.: Uniqueness in inverse boundary value problems for fractional diffusion equations. Inverse Prob. 32(1), 015004 (2016)

    MathSciNet  MATH  Google Scholar 

  21. Li, Z., Liu, Y, Yamamoto, M.: Initial-boundary value problems for multi-term time-fractional diffusion equations with positive constant coefficients. Appl. Math. Comput. 257, 381–397 (2015)

    MathSciNet  MATH  Google Scholar 

  22. Li, Z., Yamamoto, M.: Uniqueness for inverse problems of determining orders of multi-term time-fractional derivatives of diffusion equation. Appl. Anal. 94(3), 570–579 (2015)

    MathSciNet  MATH  Google Scholar 

  23. Liu, F., Meerschaert, M.M., McGough, R.J., Zhuang, P., Liu, Q.: Numerical methods for solving the multi-term time-fractional wave-diffusion equation. Fract. Calc. Appl. Anal. 16(1), 9–25 (2013)

    MathSciNet  MATH  Google Scholar 

  24. Liu, Y.: Strong maximum principle for multi-term time-fractional diffusion equations and its application to an inverse source problem. Comput. Math. Appl. 73(1), 96–108 (2017)

    MathSciNet  MATH  Google Scholar 

  25. Lorenzo, C.F., Hartley, T.T.: Variable order and distributed order fractional operators. Nonlinear Dyn. 29(1-4), 57–98 (2002)

    MathSciNet  MATH  Google Scholar 

  26. Luchko, Y.: Initial-boundary-value problems for the generalized multi-term time-fractional diffusion equation. J. Math. Anal. Appl. 374(2), 538–548 (2011)

    MathSciNet  MATH  Google Scholar 

  27. Metzler, R., Klafter, J.: Boundary value problems for fractional diffusion equations. Physica A: Statistical Mechanics and its Applications 278, 107–125 (2000)

    MathSciNet  MATH  Google Scholar 

  28. Metzler, R., Klafter, J.: The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339, 1–77 (2000)

    MathSciNet  MATH  Google Scholar 

  29. Metzler, R., Klafter, J.: Subdiffusive transport close to thermal equilibrium: from the Langevin equation to fractional diffusion. Phys. Rev. E 61, 6308–6311 (2000)

    Google Scholar 

  30. Morozov, V.A., Nashed, Z., Aries, A.B.: Methods for Solving Incorrectly Posed Problems. Springer, New York (1984)

    Google Scholar 

  31. Naber, M.: Distributed order fractional subdiffusion. Fractals 12, 23–32 (2004)

    MathSciNet  MATH  Google Scholar 

  32. Thamban Nair, M.: Linear Operator Equations: Approximation and Regularization. World Scientific, Singapore (2009)

    MATH  Google Scholar 

  33. Ou, Y.H., Hasanov, A., Liu, Z.H.: Inverse coefficient problems for nonlinear parabolic differential equations. Acta Math. Sin. (Engl. Ser.) 24(10), 1617–1624 (2008)

    MathSciNet  MATH  Google Scholar 

  34. Sokolov, I.M., Chechkin, A.V., Klafter, J.: Distributed-order fractional kinetics. Acta Phys. Polon. B 35, 1323–1341 (2004)

    Google Scholar 

  35. Sokolov, I.M., Klafter, J.: From diffusion to anomalous diffusion: a century after Einstein’s Brownian motion. Chaos 15(2), 1–7 (2005)

    MathSciNet  MATH  Google Scholar 

  36. Taylor, M.E.: Partial differential equations I. Basic Theory, Second Edition, Applied Mathematical Sciences, vol. 115. Springer, New York (2011)

    Google Scholar 

  37. Wei, L.L.: Stability and convergence of a fully discrete local discontinuous Galerkin method for multi-term time fractional diffusion equations. Numer. Algorithms 76(3), 695–707 (2017)

    MathSciNet  MATH  Google Scholar 

  38. Wei, T., Li, X.L., Li, Y.S.: An inverse time-dependent source problem for a time-fractional diffusion equation. Inverse Prob. 32, 085003 (2016)

    MathSciNet  MATH  Google Scholar 

  39. Ye, H., Gao, J.M., Ding, Y.S.: A generalized Gronwall inequality and its application to a fractional differential equation. J. Math. Anal. Appl. 328(2), 1075–1081 (2007)

    MathSciNet  MATH  Google Scholar 

  40. Yuste, S.B., Acedo, L., Lindenberg, K.: Reaction front in an A + BC reaction-subdiffusion process. Phys. Rev. E 69, 036126 (2004)

    Google Scholar 

  41. Yuste, S.B., Lindenberg, K.: Subdiffusion-limited reactions. Chem. Phys. 284, 169–180 (2002)

    Google Scholar 

  42. Zhao, Y.M., Zhang, Y.D., Liu, F., Turner, I., Tang, Y.F., Anh, V.: Convergence and superconvergence of a fully-discrete scheme for multi-term time fractional diffusion equations. Comput. Math. Appl. 73(6), 1087–1099 (2017)

    MathSciNet  MATH  Google Scholar 

  43. Zheng, M., Liu, F., Anh, V., Turner, I.: A high-order spectral method for the multi-term time-fractional diffusion equations. Appl. Math. Model. 40(7-8), 4970–4985 (2016)

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Lanzhou University, Gansu, 730000, People’s Republic of China

    Y. S. Li, L. L. Sun, Z. Q. Zhang & T. Wei

  2. School of Cyber Security, Gansu Institute of Political Science and Law, Lanzhou, 730000, People’s Republic of China

    Y. S. Li

Authors
  1. Y. S. Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. L. L. Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Z. Q. Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. T. Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to T. Wei.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This paper was supported by the NSF of China (11371181, 11771192, 11601207) and Scientific Research Project of GanSu Political Science And Law Institute (2016XZDLW16).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, Y.S., Sun, L.L., Zhang, Z.Q. et al. Identification of the time-dependent source term in a multi-term time-fractional diffusion equation. Numer Algor 82, 1279–1301 (2019). https://doi.org/10.1007/s11075-019-00654-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-019-00654-5

Keywords

Search

Navigation