Skip to main content
SpringerLink
Log in

A self-adaptive iterative algorithm for the split common fixed point problems

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

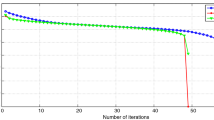
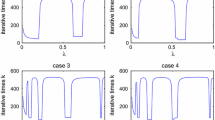
In this paper, we use the dual variable to propose a self-adaptive iterative algorithm for solving the split common fixed point problems of averaged mappings in real Hilbert spaces. Under suitable conditions, we get the weak convergence of the proposed algorithm and give applications in the split feasibility problem and the split equality problem. Some numerical experiments are given to illustrate the efficiency of the proposed iterative algorithm. Our results improve and extend the corresponding results announced by many others.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. Bauschke, H.H.: The approximation of fixed points of composition of nonexpansive mappings in Hilbert space. J. Math. Anal. Appl. 202, 150–159 (1996)

    Article  MathSciNet  Google Scholar 

  2. Bauschke, H.H., Borwein, J.M.: On projection algorithms for solving convex feasibility problems. SIAM Rev. 38, 367–426 (1996)

    Article  MathSciNet  Google Scholar 

  3. Byrne, C.: Iterative oblique projection onto convex subsets and the split feasibility problem. Inverse Probl. 18, 441–453 (2002)

    Article  Google Scholar 

  4. Byrne, C.: A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Probl. 20, 103–120 (2004)

    Article  MathSciNet  Google Scholar 

  5. Byrne, C., Censor, Y., Gibali, A., Reich, S.: The split common null point problem. J. Nonlinear Convex Anal. 13, 759–775 (2012)

    MathSciNet  MATH  Google Scholar 

  6. Chang, S.S., Kim, J.K., Cho, Y.J., Sim, J.Y.: Weak and strong convergence theorems of solutions to split feasibility problem for nonspreading type mapping in Hilbert spaces. Fixed Point Theory Appl. 2014, 11 (2014)

    Article  MathSciNet  Google Scholar 

  7. Cegielski, A.: General method for solving the split common fixed point problem. J. Optim. Theory Appl. 165, 385–404 (2015)

    Article  MathSciNet  Google Scholar 

  8. Censor, Y., Segal, A.: The split common fixed point problem for directed operators. J. Convex Anal. 16, 587–600 (2009)

    MathSciNet  MATH  Google Scholar 

  9. Censor, Y., Elfving, T.: A multiprojection algorithm using Bregman projections in a product space. Numer. Algor. 8, 221–239 (1994)

    Article  MathSciNet  Google Scholar 

  10. Censor, Y., Gibalin, A., Reich, S.: Algorithms for the split variational inequality problem. Numer. Algorithms 59, 301–323 (2012)

    Article  MathSciNet  Google Scholar 

  11. Censor, Y., Bortfeld, T., Martin, B., Trofimov, A.: A unified approach for inversion problems in intensity modulated radiation therapy. Phys. Med. Biol. 51, 2353–2365 (2006)

    Article  Google Scholar 

  12. Chen, P., Huang, J., Zhang, X.: A primal-dual fixed point algorithm for convex separable minimization with applications to image restoration. Inverse Probl. 29, 025011 (2013). (33pp)

    Article  MathSciNet  Google Scholar 

  13. Combettes, P.L.: The convex feasibility problem in image recovery. Adv. Imaging Electron Phys. 95, 155–270 (1996)

    Article  Google Scholar 

  14. Dong, Q.L., Lu, Y.Y., Yang, J.: The extragradient algorithm with inertial effects for solving the variational inequality. Optimization 65(12), 2217–2226 (2016)

    Article  MathSciNet  Google Scholar 

  15. Dong, Q.L., Yuan, H.B., Cho, Y.J., Rassias, Th.M.: Modified inertial Mann algorithm and Inertial CQ-algorithm for nonexpansive mappings. Optim. Lett. 12(1), 87–102 (2018)

    Article  MathSciNet  Google Scholar 

  16. Dong, Q.L., Tang, Y.C., Cho, Y.J., Rassias, Th.M.: Optimal choice of the step length of the projection and contraction methods for solving the split feasibility problem. J. Glob. Optim. 71, 341–360 (2018)

    Article  MathSciNet  Google Scholar 

  17. Eslamian, M., Eskandani, G.Z., Raeisi, M.: Split common null point and common fixed point problems between Banach spaces and Hilbert spaces. Mediterr. J. Math. 14, 119,15 (2017)

    Article  MathSciNet  Google Scholar 

  18. Giang, D.M., Strodiot, J.J., Nguyen, V.H.: Strong convergence of an iterative method for solving the multiple-set split equality fixed point problem in a real Hilbert space. RACSAM Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Mat. 111, 983–998 (2017)

    Article  MathSciNet  Google Scholar 

  19. Gornicki, J.: Weak convergence theorems for asymptotically nonexpansive mappings in uniformly convex Banach spaces. Comment Math. Univ. Carolin. 301, 249–252 (1998)

    MathSciNet  MATH  Google Scholar 

  20. Zhang, W., Han, D., Li, Z.: A self-adaptive projection method for solving the multiple-sets split feasibility problem. Inverse Probl. 25, 115001(16pp) (2009)

    Article  MathSciNet  Google Scholar 

  21. Lopez, G., Martin, V., Wang, F., Xu, H.K.: Solving the split feasibility problem without prior knowledge of matrix norms. Inverse Probl. 28, 085004 (2012)

    Article  MathSciNet  Google Scholar 

  22. Masad, E., Reich, S.: A note on the multiple-set split convex feasibility problem in Hilbert space. J. Nonlinear Convex Anal. 8, 367–371 (2007)

    MathSciNet  MATH  Google Scholar 

  23. Moudafi, A.: A note on the split common fixed point problem for quasi-nonexpansive operators. Nonlinear Anal. 74, 4083–4087 (2011)

    Article  MathSciNet  Google Scholar 

  24. Moudafi, A.: Alternating CQ-algorithms for convex feasibility and split fixed-point problems. J. Nonlinear Convex A. 15, 809–818 (2014)

    MathSciNet  MATH  Google Scholar 

  25. Moudafi, A., Al-Shemas, E.: Simultaneous iterative methods for split equality problems and application. Transactions on Mathematical Programming and Applications 1, 1–11 (2013)

    Google Scholar 

  26. Qin, X., Wang, L.: A fixed point method for solving a split feasibility problem in Hilbert spaces, RACSAM Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Mat. https://doi.org/10.1007/s13398-017-0476-6

    Article  MathSciNet  Google Scholar 

  27. Qin, X., Petrusel, A., Yao, J.C.: CQ Iterative algorithms for fixed points of nonexpansive mappings and split feasibility problems in Hilbert spaces. J. Nonlinear Convex Anal. 19, 157–165 (2018)

    MathSciNet  MATH  Google Scholar 

  28. Qu, B., Xiu, N.: A note on the CQ algorithm for the split feasibility problem. Inverse Probl. 21, 1655–1665 (2005)

    Article  MathSciNet  Google Scholar 

  29. Wang, F.: On the convergence of CQ algorithm with variable steps for the split equality prblem. Numer. Algor. 74, 927–935 (2017)

    Article  Google Scholar 

  30. Wang, F.: A new method for split common fixed-point problem without priori knowledge of operator norms. J. Fixed Point Theory Appl. 19, 2427–2436 (2017)

    Article  MathSciNet  Google Scholar 

  31. Witthayarat, U., Abdou, A.A., Cho, Y.J.: Shrinking projection methods for solving split equilibrium problems and fixed point problems for asymptotically nonexpansive in Hilbert spaces. Fixed Point Theory Appl. 2015, 200 (2015)

    Article  MathSciNet  Google Scholar 

  32. Xu, H.K.: A variable krasnosel’skiĭ-mann algorithm and the multiple-set split feasibility problem. Inverse Probl. 22, 2021–2034 (2006)

    Article  Google Scholar 

  33. Xu, H.K.: Iterative methods for the split feasibility problem in infinite-dimensional Hilbert spaces. Inverse Probl. 26(105018), 17 (2010)

    MathSciNet  MATH  Google Scholar 

  34. Yao, Y., Yao, Z., Abdou, A.A., Cho, Y.J.: Self-adaptive algorithms for proximal split feasibility problems and strong convergence analysis. Fixed Point Theory Appl. 2015, 205 (2015)

    Article  MathSciNet  Google Scholar 

  35. Yang, L., Zhao, F., Kim, J.K.: The split common fixed point problem for demicontractive mappings in Banach spaces. J. Comput. Anal. Appl. 22(5), 858–863 (2017)

    MathSciNet  Google Scholar 

  36. Yang, Q.: On variable-step relaxed projection algorithm for variational inequalities. J. Math. Anal. Appl. 302, 166–179 (2005)

    Article  MathSciNet  Google Scholar 

  37. Zhao, J., He, S.: Viscosity approximation methods for split common fixed-point problem of directed operators. Numer. Funct. Anal. Optim. 36, 528–547 (2015)

    Article  MathSciNet  Google Scholar 

  38. Zhao, J.: Solving split equality fixed-point problem of quasi-nonexpansive mappings without prior knowledge of operators norms. Optimization 64(12), 2619–2630 (2015)

    Article  MathSciNet  Google Scholar 

  39. Zhou, H., Wang, P.: Adaptively relaxed algorithms for solving the split feasibility problem with a new step size. Journal of Inequalities and Applications 2014, 448 (2014)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Science, Civil Aviation University of China, Tianjin, 300300, China

    Jing Zhao & Dingfang Hou

Authors
  1. Jing Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dingfang Hou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jing Zhao.

Additional information

Supported by National Natural Science Foundation of China (No. 61571441) and Scientific Research Project of Tianjin Municipal Education Commission (No. 2018KJ253).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, J., Hou, D. A self-adaptive iterative algorithm for the split common fixed point problems. Numer Algor 82, 1047–1063 (2019). https://doi.org/10.1007/s11075-018-0640-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-018-0640-x

Keywords

Mathematics Subject Classification (2010)

Search

Navigation