Abstract
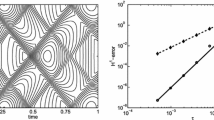
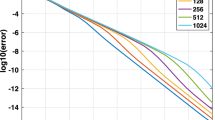
We assess the applicability and efficiency of time-adaptive high-order splitting methods applied for the numerical solution of (systems of) nonlinear parabolic problems under periodic boundary conditions. We discuss in particular several applications generating intricate patterns and displaying nonsmooth solution dynamics. First, we give a general error analysis for splitting methods for parabolic problems under periodic boundary conditions and derive the necessary smoothness requirements on the exact solution in particular for the Gray–Scott equation and the Van der Pol equation. Numerical examples demonstrate the convergence of the methods and serve to compare the efficiency of different time-adaptive splitting schemes and of splitting into either two or three operators, based on appropriately constructed a posteriori local error estimators.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Söderlind, G., Wang, L.: Adaptive time-stepping and computational stability. J. Comput. Appl. Math. 185, 225–243 (2006)
Hairer, E., Lubich, C., Wanner, G.: Geometric numerical integration. Springer-Verlag, Berlin–Heidelberg–New York (2002)
Hochbruck, M., Ostermann, A.: Exponential integrators. Acta Numer. 19, 209–286 (2010)
Descombes, S., Duarte, M., Dumont, T., Louvet, V., Massot, M.: Adaptive time splitting method for multi-scale evolutionary partial differential equations. Confluentes Math. 03, 413–443 (2011)
Jahnke, T., Lubich, C.: Error bounds for exponential operator splittings. BIT 40, 735–744 (2000)
Thalhammer, M.: High-order exponential operator splitting methods for time-dependent Schrödinger equations. SIAM J. Numer. Anal. 46(4), 2022–2038 (2008)
Lubich, C.: On splitting methods for Schrödinger–Poisson and cubic nonlinear Schrödinger equations. Math. Comp. 77, 2141–2153 (2008)
Koch, O., Neuhauser, C., Thalhammer, M.: Error analysis of high-order splitting methods for nonlinear evolutionary Schrödinger equations and application to the MCTDHF equations in electron dynamics. M2AN Math. Model. Numer. Anal. 47, 1265–1284 (2013)
Blanes, S., Casas, F., Chartier, P., Murua, A.: Optimized high-order splitting methods for some classes of parabolic equations. Math. Comp. 82, 1559–1576 (2013)
Hansen, E., Ostermann, A.: Exponential splitting for unbounded operators. Math. Comp. 78, 1485–1496 (2009)
Auzinger, W., Koch, O., Thalhammer, M.: Defect-based local error estimators for splitting methods, with application to Schrödinger equations, Part II: Higher-order methods for linear problems. J. Comput. Appl. Math. 255, 384–403 (2013)
Koch, O., Neuhauser, C., Thalhammer, M.: Embedded split-step formulae for the time integration of nonlinear evolution equations. Appl. Numer. Math. 63, 14–24 (2013)
Auzinger, W., Koch, O., Thalhammer, M.: Defect-based local error estimators for high-order splitting methods involving three linear operators. Numer. Algorithms 70, 61–91 (2015)
Auzinger, W., Hofstätter, H., Ketcheson, D., Koch, O.: Practical splitting methods for the adaptive integration of nonlinear evolution equations. Part I: construction of optimized schemes and pairs of schemes, BIT Numer. Math., published online 28 July 2016
Auzinger, W., Koch, O.: Coefficients of various splitting methods, http://www.asc.tuwien.ac.at/~winfried/splitting/
Hairer, E., Nørsett, S., Wanner, G.: Solving ordinary differential equations I. Springer-Verlag, Berlin–Heidelberg–New York (1987)
Press, W., Flannery, B., Teukolsky, S., Vetterling, W.: Numerical recipes in C — the art of scientific computing. Cambridge University Press, Cambridge (1988)
Gray, P., Scott, S.: Chemical waves and instabilities. Clarendon, Oxford (1990)
Robinson, J.: Infinite-dimensional dynamical systems. Cambridge University Press, Cambridge (2001)
Katznelson, Y.: An introduction to harmonic analysis. Dover Publications, Inc., New York (1968)
Rudin, W.: Real and complex analysis, 3rd edn. McGraw-Hill (1987)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Auzinger, W., Koch, O. & Quell, M. Adaptive high-order splitting methods for systems of nonlinear evolution equations with periodic boundary conditions. Numer Algor 75, 261–283 (2017). https://doi.org/10.1007/s11075-016-0206-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-016-0206-8