Skip to main content

A marching-on in time meshless kernel based solver for full-wave electromagnetic simulation

Numerical Algorithms volume 62, pages 541–558 (2013)Cite this article

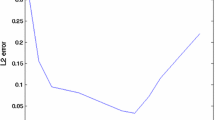
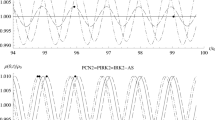
Abstract

A meshless particle method based on an unconditionally stable time domain numerical scheme, oriented to electromagnetic transient simulations, is presented. The proposed scheme improves the smoothed particle electromagnetics method, already developed by the authors. The time stepping is approached by using the alternating directions implicit finite difference scheme, in a leapfrog way. The proposed formulation is used in order to efficiently overcome the stability relation constraint of explicit schemes. In fact, due to this constraint, large time steps cannot be used with small space steps and vice-versa. The same stability relation holds when the meshless formulation is applied together with an explicit finite difference scheme accounted for the time stepping. The computational tool is assessed and first simulation results are compared and discussed in order to validate the proposed approach.

This is a preview of subscription content, access via your institution.

Access options

Buy single article

Instant access to the full article PDF.

USD 39.95

Price includes VAT (USA)
Tax calculation will be finalised during checkout.

References

  1. Ala, G., Francomano, E.: An improved smoothed particle electromagnetics method in 3D time domain simulations. Int. J. Numer. Model: Electronic Networks, Devices and Fields 25(4), 325–337 (2012)

    Article  Google Scholar 

  2. Ala, G., Francomano, E.: SPEM modelling on HPC-GRID environment. ACES Appl. Comput. Electromagn. Soc. J. 27(3), 229-237 (2012)

    Google Scholar 

  3. Ala, G., Francomano, E., Tortorici, A., Spagnuolo, A.: A meshless approach for electromagnetic simulation of metallic carbon nanotubes. J. Math. Chem. 48(1), 72–77 (2010)

    MathSciNet  MATH  Article  Google Scholar 

  4. Ala, G., Di Blasi, G., Francomano, E.: A numerical meshless particle method in solving the magnetoencefalography forward problem. Int. J. Numer. Model: Electronic Networks, Devices and Fields (2012). doi:10.1002/jnm.1828

    MATH  Google Scholar 

  5. Belytschko, T., Krongauz, Y., Organ, D., Fleming, M. Krysl, P.: Meshless methods: an overview and recent developments. Comput. Methods Appl. Mech. Eng. 139, 3–47 (1996)

    MATH  Article  Google Scholar 

  6. Cingoski, V., Miyamoto, N., Yamashita, H.: Element-free Galerkin method for electromagnetic field computations. IEEE Trans. Magn. 34(5), 3236–3239 (1998)

    Article  Google Scholar 

  7. Cooke, S.J., Botton, M., Antonsen, T.M., Levush, B.: A leapfrog formulation of the 3-D ADI-FDTD algorithm. Int. J. Numer. Model: Electronic Networks, Devices and Fields 22, 187–200 (2009)

    MATH  Article  Google Scholar 

  8. Duan, Y., Lai, S.J., Huang, T.: Coupling projection domain decomposition method and meshless collocation method using radial basis functions in electromagnetics. Prog. Electromagn. Res. Letters 5, 1–12 (2008)

    Article  Google Scholar 

  9. Fang, J., Parriaux, A., Rentschler, M., Ancey, C.: Improved SPH methods for simulating free surface flows of viscous fluids. Appl. Numer. Math. 59(2), 251–271 (2009)

    MathSciNet  MATH  Article  Google Scholar 

  10. Fonseca, A.R., Mendes, M.L., Mesquita, R.C., Silva, E.J.: A 3-D radial point interpolation method for meshless time-domain modelling. J. Microw. Optoelectron. Electromagn. Appl. 8(1), 101S–113S (2009)

    Google Scholar 

  11. Fonseca, A.R., Viana, S.A., Silva, E.J., Mesquita, R.C.: Imposing boundary conditions in the meshless local Petrov-Galerkin method. IET Sci. Meas. Technol. 2(6), 387–394(2008)

    Article  Google Scholar 

  12. Krohne, K., Gi-Ho, P., Ping, L.E.: A two-dimensional smoothed particle time-domain method. In: Asia Pacific Microwave Conference, art. no. 4958480 (2008)

  13. Lai, S.J., Wang, B.Z., Duan, Y.: Meshless radial basis function method for transient electromagnetic computations. IEEE Trans. Magn. 44(10), 2288–2295 (2008)

    Article  Google Scholar 

  14. Liu, G.R.: Mesh Free Methods: Moving Beyond the Finite Element Method. World Scientific Publishing (2003)

  15. Liu, B., Liu, G.R.: Smoothed Particle Hydrodynamics—A mesh-free particle method. World Scientific Publishing (2003)

  16. Liu, B., Liu, G.R.: Restoring particle consistency in smoothed particle hydrodynamics. Appl. Numer. Math. 56(1), 19–36 (2006)

    MathSciNet  MATH  Article  Google Scholar 

  17. Liu, B., Liu, G.R.: Smoothed particle hydrodynamics (SPH): an overview and recent developments. Arch. Comput. Methods Eng. 17(1), 25–76 (2010)

    MathSciNet  Article  Google Scholar 

  18. Liu, X., Wang, B.Z., Lai, S.: Element-free Galerkin method for transient electromagnetic field simulation. Microw. Opt. Technol. Lett. 50(1), 134–138 (2008)

    Article  Google Scholar 

  19. Mendes, M.L., Pimenta, L.C.A., Mesquita, R.C., Silva, E.J., Santana, T.C.: Smoothed particle electromagnetics with boundary absorbing condition using perfectly matched layers. IET Conference Publications, (537 CP), pp. 164–165 (2008)

  20. Mirzaei, D., Dehghan, M.: A meshless based method for solution of integral equations. Appl. Numer. Math. 60(3), 245–262 (2010)

    MathSciNet  MATH  Article  Google Scholar 

  21. Monaghan, J.J.: An introduction to SPH. Comput. Phys. Comm. 48, 89–96 (1988)

    MATH  Article  Google Scholar 

  22. Monaghan, J.J., Lattanzio, J.C.: A refined particle method for astrophysical problems. Astron. Astrophys. 149, 135–143 (1985)

    MATH  Google Scholar 

  23. Monaghan, J.J.: Smoothed particle hydrodynamics. Annu. Rev. Astron. Astrophys. 30, 543–574 (1992)

    Article  Google Scholar 

  24. Moussa, B.B.: On the convergence of SPH method for scalar conservation laws with boundary conditions. Methods Appl. Anal. 13(1), 29–62 (2006)

    MathSciNet  MATH  Google Scholar 

  25. Namiki, T.: A new FDTD algorithm based on alternating-direction implicit method. IEEE Trans. Microwave Theor. Tech. 47(10), 2003–2007 (1999)

    Article  Google Scholar 

  26. Park, G.H., Krohne, K., Bai, P., Er, P.L.: Applications of meshfree methods in electromagnetics. IET Conference Publications (537 CP), pp. 1–2 (2008)

  27. Park, G.H., Krohne, K., Bai, P., Er, P.L.: Introduction to the smoothed particle hydrodynamics method in electromagnetics. Asia-Pacific Symposium on Electromagnetic Compatibility, pp. 582–585 (2008)

  28. Sadiku, M.N.O.: Elements of Electromagnetics. Oxford University Press (2001)

  29. Shanazari, K., Rabie, N.: A three dimensional adaptive nodes technique applied to meshless-type methods. Appl. Numer. Math. 59(6), 1187–1197 (2009)

    MathSciNet  MATH  Article  Google Scholar 

  30. Soares, D. Jr.: Numerical modelling of electromagnetic wave propagation by meshless local petrov-galerkin formulations. Comput. Model. Eng. Sci. 50(2), 97–114 (2006)

    MathSciNet  Google Scholar 

  31. Sullivan, D.M.: Electromagnetic Simulation using the FDTD Method. IEEE press (2000)

  32. Taflove, A., Hagness, S.: Computational Electrodynamics: The Finite-Difference Time-Domain Method. Artech House, Boston (2000)

    MATH  Google Scholar 

  33. Viana, S.A., Mesquita, R.C.: Moving least square reproducing kernel method for electromagnetic field computation. IEEE Trans. Magn. 35(3), 1372–1375 (1999)

    Article  Google Scholar 

  34. Wang, J.G., Liu, G.R.: A point interpolation meshless method based on radial basis functions. Int. J. Numer. Methods Eng. 54, 1623–1648 (2002)

    MATH  Article  Google Scholar 

  35. Yang, E., Mo, J. Liu, H., Xu, W., Wang, S.: Modification of the weak form to enforce electromagnetic field interface conditions in element-free Galerkin method. Int. J. Appl. Electromagn. Mech. 31(3), 127–145 (2009)

    Google Scholar 

  36. Yu, Y., Chen, Z.: A 3-D radial point interpolation method for meshless time-domain modelling. IEEE Trans. Microwave Theor. Tech. 57(8), 2015–2020 (2009)

    MathSciNet  Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Università degli Studi di Palermo - DIEETCAM, Palermo, Italy

    Guido Ala

  2. Università degli Studi di Palermo - DICGIM, Palermo, Italy

    Elisa Francomano

Authors
  1. Guido Ala
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Elisa Francomano
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Elisa Francomano.

Rights and permissions

Reprints and Permissions

About this article

Cite this article

Ala, G., Francomano, E. A marching-on in time meshless kernel based solver for full-wave electromagnetic simulation. Numer Algor 62, 541–558 (2013). https://doi.org/10.1007/s11075-012-9635-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-012-9635-1

Keywords

  • Alternating directions implicit scheme
  • Finite difference time domain
  • Meshless methods
  • Electromagnetic transient analysis

Mathematics Subject Classifications (2010)

  • 35Q61
  • 65D25