Flexural–torsional modal interaction in MEMS actuators initiated by minuscule asymmetry

Abstract

An efficient actuation technique for electrostatic MEMS actuators exploiting electro-mechanical-mechanical modal interactions is proposed. The flexural–torsional equations of motion are established, and we manifest that the initiation of a 2:1 autoparametric modal interaction between in-plane bending and torsional modes of the actuator that is supposed to be symmetrical with respect to its axis of rotation is contingent upon the presence of a quadratic stiffness term, which arises from the existence of non-zero first moments of area of the actual cross-section in prismatic microbeams. In order to efficiently reduce the AC voltage value required to reach the activation of the 2:1 mechanical modal interaction, the electrical resonant frequency is syntonized to half of the natural frequency of the in-plane bending mode. The results indicate that the amplitude of the in-plane motion saturates upon the initiation of an energy exchange between the bending and torsional motions. Through suitable tuning of the AC frequency, the amplitude of the in-plane motion is minimized, while the amplitude of the torsional motion, the indirectly excited mode, is maximized. Our results demonstrate that the actuator's torsional motion, when subjected to a 1:2:1 electro-flexural–torsional modal interactions, is triggered by applying a maximum voltage of 10 V, resulting in about 20 degrees rotational angle. Furthermore, prolific frequency combs are generated as a result of secondary Hopf bifurcations along the large-amplitude response branches, inducing quasi-periodicity in the MEMS dynamics.

1 Introduction

This section provides a brielf literature survey on internal resonance studies in electro-mechanical systems and the flexural–torsional vibration of beam structures.

1.1 Internal resonance in MEMS

Special thanks to the rich dynamics provided by modal interactions, this phenomenon have been the focus of many researchers working on nonlinear dynamic systems with the aim of improving working principles in electro-mechanical devices, such as sensors and actuators. To observe this phenomenon, there should be a commensurate ratio of one-to-one [1,2,3,4], one-to-two [5], two-to-one [6, 7], one-to-three [8,9,10,11], three-to-one [12,13,14], etc., between at least two modes of the system. Under these conditions, the system's response is contributed by both of those two modes when one mode is directly excited using either an external drive or a parametric pump, while the other one is indirectly excited through an energy exchange between the two engaged modes. In electro-mechanical systems, the two involved modes can consist of either both mechanical modes or one mechanical and one electrical mode [15]. Among the above-stated cases, particularly in the context of two-to-one internal resonance, where the high-frequency (HF) mode is directly excited, creating an indirect forcing signal for the low-frequency (LF) mode, the inclusion of quadratic nonlinearity is crucial for establishing an autoparametric energy channel between the two modes. Additionally, there exists a threshold, referred to as the activation level of modal interaction, where excitation amplitudes below this value result in the system's response being solely constructed by the HF mode.

Modal interactions have proven to be highly beneficial in Micro-Electro-Mechanical-Systems (MEMS), where implementing working principles exploiting the dynamic characteristics introduced by modal interactions, enhances the performance of MEMS sensors [3, 13, 16,17,18] and actuators [19,20,21,22]. Many valuable studies have been conducted on modal interactions in electrostatic MEMS made of clamped–clamped straight microbeams [5, 23,24,25,26] and compound structures [27,28,29,30] with the application of frequency stabilization [11, 31,32,33], mass sensing [8, 17, 18, 34], frequency combs generation [35,36,37], angular rate sensing [16, 38, 39].

There has been a wealth of published research studying the dynamics of symmetric [25, 34, 40,41,42,43,44,45,46] and asymmetric [14, 26, 47,48,49,50] electrostatic MEMS resonators. Those works investigate mechanical-mechanical modal interactions, delving into both experimental and numerical analyses to explore the intricate steady-state frequency- and force-response behaviors of such systems. Analytical investigation addressing the frequency- and force-response behaviors of the similar device featuring three-to-one internal resonance between its first anti-symmetric and second symmetric bending modes was conducted in [13].

In recent years, the examination of modal interaction in electrostatic MEMS resonators made of curved beams has gained the attention of many researchers [35, 51,52,53,54,55,57]. The nonlinear free and forced vibration characteristics of a shallow double-arch MEMS resonator featuring 1:2 internal resonance between its first and second in-plane symmetric bending modes were studied in [54]. Although employing a continuum-based model for their MEMS resonator is straightforward, the authors opted for the assumption of two third-order polynomials to fit the system's mechanical restoring forces. They conducted an extensive series of static simulations utilizing Finite Element Method (FEM) to determine the coefficients of those polynomials. However, this process, specific to the structure's dimensions for the same design, should be repeated for each set of geometry and material properties, bona fide. They explored the loci of secondary Hopf bifurcations concerning the system's parameters, yielding low-density phononic frequency combs including at most nineteen teeth. They performed experimental studies for the same device in [35]. The nonlinear dynamics of clamped–clamped straight and arch beams were examined based on parametrizing the Reduced Order Model (ROM) of the systems along the invariant manifold corresponding to the subset of their eigenfunctions [57]. However, the proposed fitting method fails to provide insights into the origins of the estimated nonlinear stiffness terms.

1.2 Flexural–torsional vibration

Some of the valuable studies inspecting the flexural–torsional vibration in mechanical resonators are addressed in the following. The nonlinear flexural–torsional vibration of beams having symmetric cross-sections with two axes of symmetry, where the shear center aligns with the cross-sectional centroid, is investigated in [30, 58,59,60,61].

Vyas et al. [30] examined the two-to-one modal interaction between the in-plane bending and torsional modes of a clamped–clamped compound resonator under electrostatic excitation. Nevertheless, their design intentionally features asymmetry with respect to the axis of rotation, resulting in significant quadratic inertia and stiffness terms in the torsional equation of motion. However, their equations of motion do not account for the expected two-to-one flexural–torsional internal resonance in symmetrical electrostatic MEMS.

Luongo [62] theoretically examined the statics, dynamics, buckling and aeroelastic stability of planar cellular beams. He demonstrated that by employing the concept of shear factor, inspired by the methodology utilized to incorporate the de Saint–Venant outcomes into the Timoshenko beam theory, it becomes feasible to consider the warping of cross-sections within a rigid cross-section model. Free and forced linear dynamics of a homogeneous beam structures were studied in [63]. Their results reveals that the bending of the transverse fibers contributes negligibly to the strain potential energy compared to the extension of the longitudinal fibers.

The linear and nonlinear flexural–torsional vibration behaviors of beams with asymmetric cross-sections, or cross-sections having one axis of symmetry, are examined in [64,65,66,67,68,69,70,71,72]. Mukherjee et al. [72] established the equations of motion for the coupled bending-torsional vibration in thin-walled beam structures with asymmetric closed cross-sections. Their equations of motions, however, fail to account for the two-to-one modal interaction between the flexural and torsional motions when simplifying the cross-section geometry to be symmetrical.

Based on the existing literature, the development of continuum-based equations of motion capable of representing the 2:1 modal interaction between bending and torsional motions in symmetrically designed structures has yet to be addressed. In this work, we introduce flexural–torsional equations of motion tailored for an electrostatic MEMS actuator that by design is symmetric with respect its axis of rotation. To this, we incorporate the impact of cross-sectional imperfection along with the concept of absolute slopes of tangents to the beam element's middle-fiber, never explored before, into the mathematical model. We study the 2:1 flexural–torsional internal resonance in a compound electrostatic MEMS actuator, where indirect excitation of the torsional mode efficiently improves the amplitude of the actuator's rotational motion. First, we aim to unravel the origin of the quadratic nonlinear stiffness that couples the in-plane bending and out-of-plane rotational motions in symmetrically designed beam structures, employing continuum mechanics [73,74,75,76,77]. It is imperative to underscore that mathematical models for prismatic microbeams with ideally symmetric cross-sections may fall short in encapsulating the 2:1 bending-torsional modal interaction, unless meticulous attention is dedicated to the incorporation of cross-sectional asymmetry. Second, our goal is to reduce the internal resonance activation level by electro-mechanical/bending resonance syntonization. This enables us to achieve a potent drive for out-of-plane rotation through indirect excitation, auto-parametrically transferring vibration energy from the in-plane bending mode to the torsional mode, resulting in a supply of approximately 10 V.

2 Cross-sectional imperfection

This section begins with a question: How about considering cross-sectional asymmetry, which results from imperfections in the fabrication of microbeams, when deriving their equations of motion?

In general, the fabrication of micro-scale devices inevitably introduces tolerances in the geometric and material properties of microstructures, making the achievement of perfect fabrication with zero tolerance virtually unattainable. Those imperfections can manifest in various ways: (1) deviations in feature dimensions and shapes [78]; (2) surface roughness [79]; (3) misalignment between distinct layers or components [80, 81]; (4) residual stresses [82]; (5) material impurities [83]; (6) etching undercutting [84]; (7) misalignment of masks in photolithography [85]; (8) defects in thin films [86]; (9) inadequate adhesion [87].

Among the aforementioned categories of imperfections, those leading to disparities between the geometric dimensions specified in design layout for symmetric structures and dimensions of the fabricated device can occasionally have a constructive impact, serving as a catalyst for the occurrence of a nonlinear dynamic phenomenon. In this study, we demonstrate that a minuscule misalignment of the centroid in the rectangular cross-section of microbeam suspensions creates a pathway for vibration energy exchange between bending and torsional motions. This misalignment generates a non-zero first moment of area, appearing in the coefficients of quadratic bending-torsional coupling terms, significantly contributing to the initiation of a 2:1 bending-torsional autoparametric modal interaction.

Referring to the literature of continuum-based vibration modeling for prismatic microbeams featuring symmetric cross-sections [26, 29, 73, 77, 88], it is conventional to position the Lagrangian coordinate system along the beam's pure bending neutral axis (NA). For homogeneous microbeams, this neutral axis passes through the geometric center of the beam's cross-section. Nonetheless, owing to imperfections in the fabrication of micro-scale devices, a slight deviation exists between the positions of the ideal and actual neutral axes, as illustrated in Fig. 1. In this figure and thereafter throughout the text, “ideal C” and “actual C” represent the geometric centroids of the ideal and actual cross-sections of a homogenous microbeam, respectively.

Fig. 1

Schematic of microbeams with rectangular cross-section. The dashed black lines show the ideal profile of the beam

It is worth noting that following the three-dimensional modelling (direct) approach, we realize the structures' global modes, where all three degrees of freedom ${u}_{x}(x,y,z;t)$, ${u}_{y}(x,y,z;t)$, and ${u}_{z}$($x,y,z;t$) have contribution in constructing the vibration modes. The “direct approach” can capture the flexural–torsional modal interaction in the structures that are designed to be symmetrical without a necessary inclusion of cross-sectional imperfection.

Figure 1 depicts a schematic of microbeams having a rectangular cross-section with its ideal and actual surface profiles. The Lagranigan coordinate system, denoted as $OXYZ$, is positioned at the beam's left end center, with the X-axis aligned along the longitudinal axis of the beam coinciding with the beam's ideal NA. The ideal and actual cross-sectional profiles of the microbeam are shown at two different longitudinal positions, distinguished by blue and red colors, respectively. The scattered green curve, perturbed non-deterministically around the X-axis in three-dimensional space, depicts the locus of positions for the actual C. It is important to emphasize that the deviation in positions between the ideal and actual neutral axes (NAs) is exaggerated in the figure for the sake of visual clarity and presentation. Further discussions regarding the incorporation of cross-sectional asymmetry into the mathematical model are provided in Appendix A.

3 Actuator's design and dynamics

Figure 2 illustrates an electrostatic MEMS actuator composed of two microbeams and a rigid plate in between. The two beams are identical, with a length of $L$, width of $b$, and thickness $h$, which are clamped at one end and connected to the plate at their other ends. The plate's length, width, and thickness, are denoted by ${l}_{p}$, ${b}_{p}$, and ${h}_{p}$, respectively. The MEMS is made from silicon, with Young modulus of $E=128\text{ GPa}$, Poisson's ratio of $\nu =0.22$, and density of $\rho =2230\text{ kg}/{\text{m}}^{3}$. The resonator is equipped with an in-plane U-shaped actuating electrode on one side, spanning the entire length of the structure, forming an electrostatic MEMS capacitance. The initial capacitive gap is denoted by ${\text{g}}_{0}$. The resonator is directly excited in-plane via applying an AC waveform with an amplitude of ${V}_{AC}$ and a frequency of $\Omega$, $V\left(t\right)={V}_{AC}\text{cos}(\Omega t)$, between the side and the movable electrodes. The detailed derivations of the actuator's EoM are present in Appendix B.

Fig. 2

Schematic of the electrostatic MEMS actuator and its RLC circuit

This section presents the electro-mechanical equations of motion employed to describe electro-flexural–torsional modal interactions in the proposed electrostatic MEMS actuator. To reduce the amplitude of the supplied voltage, the electrical resonant frequency of the electrical circuit is set to match with half of the natural frequency of the first in-plane bending mode, ${\omega }_{e}=\frac{1}{\sqrt{{L}_{e}{C}_{0}}}\approx \frac{1}{2}{\omega }_{b}^{1}$, via properly adjusting the circuit's inductance value. Here, ${L}_{e}$ and ${C}_{0}$ denote the inductance and the nominal capacitance of the RLC circuit, respectively. When AC frequency is swept in the vicinity of half of the in-plane bending mode's natural frequency, the electrical current ($\dot{Q}$) undergoes resonance. This amplifies the voltage across the MEMS capacitance, thereby intensifying the electrostatic force and torque that occur at twice the AC frequency [15]. To achieve this, we describe the dynamics of the electrical side of the MEMS using a single degree-of-freedom RLC model

$${L}_{e}\ddot{Q}+{R}_{e}\dot{Q}+\frac{1}{{C}_{tot}}Q={V}_{AC}\text{cos}(\Omega t)$$

(1)

where ${L}_{e}$ and ${R}_{e}$ denote the inductance and resistance of the RLC circuit, respectively. ${C}_{m}$ represents the capacitance of the half-structure MEMS, defined as follows

$$ \begin{gathered} C_{tot} \left( t \right) = C_{m} \left( t \right) + C_{a} \left( t \right) , C_{m} \left( t \right) = C_{m}^{b} \left( t \right) + C_{m}^{p} \left( t \right), \hfill \\ C_{m}^{b} \left( t \right) = \left\{ {\begin{array}{*{20}c} {\mathop \smallint \limits_{0}^{L} \mathop \smallint \limits_{{ - \frac{b}{2}}}^{{\frac{1}{2}\left( {\frac{b - h \sin \phi }{{\cos \phi }}} \right)}} \frac{ \in }{{\left( { - \sqrt {\frac{{h^{2} }}{4} + \zeta^{2} } {\text{cos}}\left( {\tan^{ - 1} \left( {\frac{2\zeta }{h}} \right) + \phi \left( {s;t} \right)} \right) + {\text{g}}_{{\text{o}}} + \frac{h}{2} - w\left( {s;t} \right)} \right)}}d\zeta ds ;}\; { 0 \le \phi < 2\tan^{ - 1} \left( \frac{b}{h} \right)} \\ {\mathop \smallint \limits_{0}^{L} \mathop \smallint \limits_{{ - \frac{1}{2}\left( {\frac{b + h \sin \phi }{{\cos \phi }}} \right)}}^{\frac{b}{2}} \frac{ \in }{{\left( { - \sqrt {\frac{{h^{2} }}{4} + \zeta^{2} } {\text{cos}}\left( {\tan^{ - 1} \left( {\frac{2\zeta }{h}} \right) + \phi \left( {s;t} \right)} \right) + {\text{g}}_{{\text{o}}} + \frac{h}{2} - w\left( {s;t} \right)} \right)}}d\zeta ds ;}\; { - 2\tan^{ - 1} \left( \frac{b}{h} \right) < \phi \le 0 } \\ \end{array} } \right. \hfill \\ C_{m}^{p} \left( t \right) = \left\{ {\begin{array}{*{20}c} {\mathop \smallint \limits_{{ - \frac{{b_{p} }}{2}}}^{{\frac{1}{2}\left( {\frac{{b_{p} - h_{p} \sin \phi }}{\cos \phi }} \right)}} \frac{{ \in l_{p} }}{{2\left( { - \sqrt {\frac{{h_{p}^{2} }}{4} + \zeta^{2} } {\text{cos}}\left( {\tan^{ - 1} \left( {\frac{2\zeta }{{h_{p} }}} \right) + \phi \left( {s;t} \right)} \right) + {\text{g}}_{{\text{o}}} + \frac{{h_{p} }}{2} - w\left( {s;t} \right)} \right)}}d\zeta ;}\; {0 \le \phi \left( {L;t} \right) < 2\tan^{ - 1} \left( {\frac{{b_{p} }}{{h_{p} }}} \right)} \\ {\mathop \smallint \limits_{{ - \frac{1}{2}\left( {\frac{{b_{p} + h_{p} \sin \phi }}{\cos \phi }} \right)}}^{{\frac{{b_{p} }}{2}}} \frac{{ \in l_{p} }}{{2\left( { - \sqrt {\frac{{h_{p}^{2} }}{4} + \zeta^{2} } {\text{cos}}\left( {\tan^{ - 1} \left( {\frac{2\zeta }{{h_{p} }}} \right) + \phi \left( {s;t} \right)} \right) + {\text{g}}_{{\text{o}}} + \frac{{h_{p} }}{2} - w\left( {s;t} \right)} \right)}}d\zeta ;}\; { - 2\tan^{ - 1} \left( {\frac{{b_{p} }}{{h_{p} }}} \right) < \phi \left( {L;t} \right) \le 0 } \\ \end{array} } \right. \hfill \\ \end{gathered} $$

(2)

Here, ${C}_{m}$ represents the MEMS capacitance that is composed of ${C}_{m}^{b}$, the portion contributed by the flexible microbeam, and ${C}_{m}^{p}$, the portion contributed by the rigid plate. The auxiliary capacitance, denoted as ${C}_{a}$, is installed in parallel to the MEMS capacitance. According to the MEMS geometry provided in Table 1, the value of the MEMS capacitance at its rest configuration falls within the pF range. Thus, by setting ${C}_{a}=1 \text{nF}$ and ${L}_{e}=35 \text{mH}$, the electrical resonance is positioned at half of the natural frequency of the first in-plane bending mode. It is noteworthy that the total capacitance, ${C}_{tot}$, is predominantly influenced by the auxiliary capacitance, ${C}_{a}$. Consequently, variations in the MEMS capacitance are unlikely to significantly mistune the electrical resonance. Further, it should be mentioned that the MEMS capacitance formed by the plate's sides perpendicular to the microbeam's longitudinal axis and the stationary electrode is disregarded. Taking them into account would introduce a modification in the pF range, which is overshadowed by the auxiliary capacitance.

Table 1 The geometry of the electrostatic MEMS

The electrical equation, Eq. (1), is nonlinearly coupled with the mechanical side through the MEMS capacitance. Substituting $w\left(s;t\right)=\sum_{i=1}^{N=3}{q}_{i}(t){\Psi }_{\text{i}}\left(s\right)$ and $\phi \left(s;t\right)=\sum_{i=1}^{N=3}{p}_{i}(t){\Phi }_{\text{i}}\left(s\right)$ into Eqs. (A.28), (A.29), and (A.30), applying the Galerkin's method, and using integration by part to satisfy the dynamic boundary conditions in Eq. (A.30), it yields a set of six second-order nonlinear ODEs coupled to Eq. (1), which describe the following electro-mechanical equations of motion for the MEMS:

$$ \begin{aligned} &\mathop \sum \limits_{i = 1}^{N} \mathop q\nolimits_{i} \delta_{ni} + c_{w} \mathop \sum \limits_{i = 1}^{N} K_{ni}^{l\left( 1 \right)} \dot{q}_{i} + \left( {\alpha_{2} - \alpha_{5} } \right)\mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \mathop \sum \limits_{k = 1}^{N} p_{i} p_{j} \mathop q\nolimits_{k} K_{nijk}^{1} \hfill \\ &\quad + 2\left( {\alpha_{2} - \alpha_{5} } \right)\mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \mathop \sum \limits_{k = 1}^{N} p_{i} \dot{p}_{j} \dot{q}_{k} K_{nijk}^{1} + 2\left( {\alpha_{2} - \alpha_{5} } \right)\mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \mathop \sum \limits_{k = 1}^{N} p_{i} p_{j} \mathop q\nolimits_{k} K_{nijk}^{2} \hfill \\ &\quad + 2\left( {\alpha_{2} - \alpha_{5} } \right)\mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \mathop \sum \limits_{k = 1}^{N} p_{i} \dot{p}_{j} \dot{q}_{k} K_{nijk}^{2} + 2\left( {\alpha_{2} - \alpha_{5} } \right)\mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \mathop \sum \limits_{k = 1}^{N} p_{i} \dot{p}_{j} \dot{q}_{k} K_{nijk}^{3} \hfill \\ &\quad + \alpha_{1} \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \mathop \sum \limits_{k = 1}^{N} q_{i} q_{j} q_{k} K_{nijk}^{\delta \left( 1 \right)} + 4\alpha_{1} \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \mathop \sum \limits_{k = 1}^{N} q_{i} q_{j} q_{k} K_{nijk}^{\delta \left( 2 \right)} \hfill \\ &\quad + \alpha_{1} \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \mathop \sum \limits_{k = 1}^{N} q_{i} q_{j} q_{k} K_{nijk}^{\delta \left( 3 \right)} - \frac{{\alpha_{1} }}{L}\mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \mathop \sum \limits_{k = 1}^{N} q_{i} q_{j} q_{k} K_{nijk}^{\delta \left( 4 \right)} \hfill \\ &\quad - \alpha_{4} \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \mathop \sum \limits_{k = 1}^{N} q_{i} q_{j} q_{k} K_{nijk}^{ms} -{\alpha }_{1}\sum_{i=1}^{N}{K}_{ni}^{l\left(2\right)}{q}_{i}+\left({\alpha }_{6}-{\alpha }_{1}\right)\sum_{i=1}^{N}\sum_{j=1}^{N}\sum_{k=1}^{N}{p}_{i}{p}_{j}{q}_{k}{K}_{nijk}^{c\left(1\right)}\\ & \quad+4\left({\alpha }_{6}-{\alpha }_{1}\right)\sum_{i=1}^{N}\sum_{j=1}^{N}\sum_{k=1}^{N}{p}_{i}{p}_{j}{q}_{k}{K}_{nijk}^{c\left(2\right)}+2\left({\alpha }_{6}-{\alpha }_{1}\right)\sum_{i=1}^{N}\sum_{j=1}^{N}\sum_{k=1}^{N}{p}_{i}{p}_{j}{q}_{k}{K}_{nijk}^{c\left(3\right)}\\ & \quad+2\left({\alpha }_{6}-{\alpha }_{1}\right)\sum_{i=1}^{N}\sum_{j=1}^{N}\sum_{k=1}^{N}{p}_{i}{p}_{j}{q}_{k}{K}_{nijk}^{c\left(4\right)}={F}_{n}\left(t\right) \hfill \\ \end{aligned} $$

(3)

$$\sum_{i=1}^{N}{\ddot{p}}_{i}{\delta }_{ni}+{c}_{\phi }\sum_{i=1}^{N}{Kt}_{ni}^{l\left(1\right)}{\dot{p}}_{i}+\left({\beta }_{5}-{\beta }_{6}\right)\sum_{i=1}^{N}\sum_{j=1}^{N}\sum_{i=k}^{N}{p}_{i}{\dot{q}}_{j}{\dot{q}}_{k}{Kt}_{nijk}^{c\left(1\right)}+\left({\beta }_{4}-{\beta }_{3}\right)\sum_{i=1}^{N}\sum_{j=1}^{N}\sum_{i=k}^{N}{p}_{i}{q}_{j}{q}_{k}{Kt}_{nijk}^{c\left(2\right)}+{\beta }_{1}\sum_{i=1}^{N}{Kt}_{ni}^{l\left(2\right)}{p}_{i}-{\beta }_{q}\sum_{i=1}^{N}\sum_{j=1}^{N}{p}_{i}{q}_{j}K{t}_{nij}^{q}={F}_{n}^{t}(t)$$

(4)

where the components of the linear, quadratic, and cubic stiffness matrices along with the electrostatic force and torque for the ${n}^{th}$ bending and torsional modes are defined in Appendix C. To analyse the MEMS's nonlinear dynamics using semi-analytical techniques, we better to approximate the electrostatic force and torque presented in Eqs. (A.28), (A.29), and (A.30) by nonlinear polynomials that are expressed single-valued functions.

4 Results and discussions

4.1 Electro-flexural–torsional modal interactions: Periodicity

We demonstrate the impact of geometry imperfection on the inception of the 2:1 modal interaction between a bending and a torsional mode in symmetrically designed electrostatic MEMS. Here, we show that the presence of minuscule asymmetry arising from imperfections in the cross-sectional profile of the suspension microbeams results in the creation of an energy pathway between the actuator's in-plane bending and torsional modes. This occurs when there exists a nearly 2:1 ratio between the natural frequencies of the first in-plane and the first torsional modes, and the torsional mode is autoparametrically excited from above.

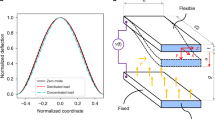
The steady-state dynamic response of the structure operating under electrostatic excitation, for three different values of ${z}_{0}$ (z-component of the centroid of the microbeam's cross-section) is illustrated in Fig. 3. Figure 3a and b depict the frequency–response curves for the in-plane bending displacement and rotation angle at the tip of the beam, respectively, with ${z}_{0}$ set at 3.5% of the beam's thickness, ${z}_{0}=0.035 h$. Here, the unbiased voltage amplitude is ${\text{V}}_{\text{AC}}=88\text{ V}$, and the bending and torsional viscous damping parameters are set to be ${c}_{w}=0.042$ and ${c}_{\phi }=0.003$, respectively. To directly excite the first in-plane bending mode, the AC frequency is swept in the vicinity of half of this mode's natural frequency. Figure 3a illustrates that the amplitude of the bending motion enhances along a small-amplitude branch until it reaches a cyclic-fold (CF) bifurcation at $2\Omega =1.985$ as the AC frequency grows from lower frequencies. However, the torsional motion extends along the trivial branch. By backward sweeping the AC frequency at this turning point, the stability of the MEMS is lost, and the bending motion transitions to a large-amplitude branch, whereas the torsional motion remains trivial. Setting the forcing frequency at $2\Omega =2.10$, and performing a backward sweep of the parameter, the in-plane motion's amplitude gradually increases as the forcing frequency approaches the natural frequency of the bending mode. However, the torsional motion remains trivial. This trend continues until reaching $2\Omega =2.0107$. Further decreasing the forcing frequency, the response undergoes a primary Hopf (HP₂) bifurcation, leading to instability in the system's response. Continuing backward along this branch, the unstable response observes a reverse primary Hopf (HP₁) bifurcation at $2\Omega =1.9811$, retrieving stability on the large-amplitude branch. The periodic orbits of the bending motion continue to expand along this branch until dynamic pull-in occurs. Up to this point, the MEMS's frequency-resposne behavior is not contributed by modal interaction between the bending and the torsional modes. To observe the formation of an energy channel between the two motions, we set the force frequency at $2\Omega =2.003$ and perform a single run using the long-time integration method, for zero initial conditions. With a sufficiently large AC voltage amplitude (${\text{V}}_{\text{AC}}=88\text{ V}$), which exceeds the activation threshold for a 2:1 modal interaction between the in-plane bending and torsional modes, the steady-state dynamic response of the MEMS is attracted to a stable periodic orbit that coexists with the previously discussed large-amplitude unstable branch. This solution, marked by a green star in Fig. 3a, is contributed by a non-trivial torsional motion, initiated through an energy exchange between this motion and the in-plane bending mode. Taking this stable response as a starting point, we continued the MEMS dynamics along the 2:1 IR-branch (branch on which the bending and the torsional motions interact) via backward sweeping the AC frequency. The amplitude of the bending motion decreases to a minimum, while the amplitude of the torsional motion increases to a maximum, occurring at $2\Omega =1.9994$. Further decreasing the AC frequency, the MEMS surpasses its extrema, with a notable increase in the amplitude of the bending motion and a corresponding decrease in the amplitude of the torsional motion and it continues until the system's dynamics experience a secondary Hopf (S-HP₁) at $2\Omega =1.9933$. At this point, the MEMS response transitions to a quasi-periodic regime, leading to the formation of local frequency combs centered around the forcing frequency and its higher harmonics. This will be discussed in the following. To capture the right-half of the 2:1 IR-branch, we return back to the starting point and continue the MEMS dynamics via forward sweeping the AC frequency. Likewise, the amplitude of the periodic orbits for bending motion expands, while the torsional motion's amplitude diminishes when transitioning to higher forcing frequencies. As seen in Fig. 3a and b, the maximum rotation angle of the plate happens at the frequency at which the in-plane bending motion is at its lowest level. In essence, the in-plane transverse and torsional motions exhibit contrasting behaviors, signifying that as one amplitude increases, the other decreases, while the MEMS operates within the 2:1 modal interaction regime. Figure 3c and d depict the frequency–response behaviors of the MEMS with a reduced misalignment in the position of the cross-sectional centroid, ${z}_{0}=0.025 h$.

Fig. 3

Frequency-displacement behavior of the MEMS actuator depicting the influence of the cross-sectional imperfection on the steady-state dynamics of the microstructure in-plane bending and torsional motions. The system's damping parameters are set to be ${c}_{w}=0.042, {c}_{\phi }=0.003$, and ${\text{V}}_{\text{AC}}=88\text{ V}$. (a), (c), and (e) illustrate the in-plane displacement for: ${z}_{0}=0.035 h$, ${z}_{0}=0.025 h$, and ${z}_{0}=0.01 h$, respectively. Correspondingly, the rotation angle at the tip of the suspension microbeams, for ${z}_{0}=0.035 h$, ${z}_{0}=0.025 h$, and ${z}_{0}=0.01 h$ are shown in (b), (d), and (f)

The results indicate that the overall dynamics remain consistent with the previous case, albeit with the distinction that the large amplitude unstable branch and the frequency range where modal interaction occurs are shortened. Further decreasing the value of ${z}_{0}$ to $0.01 h$ results in the disappearance of the M-shape frequency–response curve for the bending motion, Fig. 3e. This leads to the conclusion that increased symmetry in the beam cross-section corresponds to a higher activation level for the 2:1 modal interaction between the flexural and torsional motions. Consequently, in symmetrically designed electrostatic MEMS, with extremely small offsets in the position of the cross-sectional centroid, the microstructure undergoes pull-in before the triggering of torsional motion through a 2:1 internal resonance between the torsional and in-plane bending modes.

Figure 4 illustrates the electrostatic MEMS dynamic responses for three different values of the transverse viscous damping coefficient and AC voltage amplitude: 1) ${c}_{w}=0.042, {\text{V}}_{\text{AC}}=88\text{ V}$, 2) ${c}_{w}=0.032, {\text{V}}_{\text{AC}}=77\text{ V}$, and 3) ${c}_{w}=0.022, {\text{V}}_{\text{AC}}=65\text{ V}$, for ${z}_{0}=0.035 h$. Here, the torsional viscous damping parameter remains as previous, ${c}_{\phi }=0.003$. As seen, decreasing the damping parameter from 0.042 to 0.032 advances the activation level of the internal resonance, reducing the AC voltage amplitude by 10 V. This prevents the occurrence of cyclic-fold bifurcation and the emergence of a large-amplitude unstable branch following it. Moreover, the merging of stable periodic solutions from the left non-IR-branch with the first secondary Hopf-bifurcation (S-HP₁) located on the 2:1 IR-branch leads to the onset of period-doubling bifurcation, PD. Here, the MEMS's response along the 2:1 IR-branch until reaching the forcing frequency at which primary Hopf bifurcation (HP) occurs is entirely characterized by stable periodic orbits. Nevertheless, with a further reduction in the damping parameter to 0.022 and a corresponding decrease in the waveform amplitude to 65 V, the system displays dynamics similar to those depicted in Fig. 3a. Comparing Fig. 4a and e reveals that decreasing the damping parameter and AC voltage amplitude avoids the MEMS from undergoing cyclic-fold bifurcation; expands the large-amplitude unstable branch situated between the two primary Hopf bifurcations, HP₁ and HP₂; leads the left stable branch of the M-shape frequency–response curve to bifurcate at $2\Omega =1.9938$ under a period-doubling bifurcation, PD; and confines the quasi-periodic regime to a frequency range determined by a secondary Hopf bifurcation, S-HP, and the right peak of the M-shaped curve where a primary Hopf bifurcation (HP₂) occurs on the right large-amplitude solution branch. Referring to Fig. 4d and f, it is evident that with lower values of the linear damping parameter and AC voltage load, the maximum rotation angle of the plate decreases. However, it allows the plate to undergo either exclusively non-trivial stable rotations or primarily non-trivial stable rotations accompanied by quasi-periodicity, confined within a narrow frequency range along the 2:1 IR-branch. However, this scenario differs in Fig. 4b, where a relatively broad frequency range (between HP₁ and S-HP₁) exists, in which the system's motions are determined to be quasi-periodic. Therefore, it is concluded that to enhance stability in the MEMS operating under the 2:1 modal interaction, we need to set a balance between the damping parameter and the applied voltage amplitude. A similar analysis is performed for the case where the overall offset between the centroid of the actual cross-section and that of the ideal one is set to be 2.5% of the microbeam's thickness, ${z}_{0}=0.025 h$. Figure 5 shows that this minuscule imperfection in the centroid position of the microbeam cross-section, preventing the first moment of area of the microbeam's cross-section from vanishing (non-zero coefficients for the necessary quadratic nonlinearity coupling the bending and torsional motions), is sufficient to instigate the creation of an energy channel bridging the in-plane bending and torsional motions. The overall dynamics of the system is replicated for the same parameters' values, with the difference that the frequency range of the 2:1 IR-branch becomes more restricted for enhanced symmetry in the microbeam's cross-section.

Fig. 4

The influence of the transverse viscous damping on the frequency-displacement behavior of the MEMS, for ${z}_{0}=0.035 h$ and${c}_{\phi }=0.003$. The figure illustrates the frequency–response curves for the in-plane displacement of the microbeam's tip, for: (a) ${c}_{w}=0.042$ and ${\text{V}}_{\text{AC}}=88\text{ V}$, (c) ${c}_{w}=0.032$ and${\text{V}}_{\text{AC}}=77\text{ V}$, and (e) ${c}_{w}=0.022$ and${\text{V}}_{\text{AC}}=65\text{ V}$. The amplitudes of the rotational motion at the tip of the microbeam versus the forcing frequency are shown in (b), (d) and (f) corresponding to the parameter sets defined in (a), (c), and (e)

Fig. 5

The influence of the transverse viscous damping on the frequency-displacement behavior of the MEMS, for ${z}_{0}=0.025 h$ and${c}_{\phi }=0.003$. The figure illustrates the frequency–response curves for the in-plane displacement of the microbeam's tip, for: (a) ${c}_{w}=0.042$ and ${\text{V}}_{\text{AC}}=88\text{ V}$, (c) ${c}_{w}=0.032$ and${\text{V}}_{\text{AC}}=77\text{ V}$, and (e) ${c}_{w}=0.022$ and${\text{V}}_{\text{AC}}=65\text{ V}$. Correspondingly, the amplitudes of the rotational motion at the tip of the microbeam versus the forcing frequency are shown in (b), (d) and (f)

The steady-state dynamics of the MEMS is examined via freezing the AC voltage frequency at $\Omega =1.0002$, for the following parameters: ${z}_{0}=0.035 h$, ${c}_{w}=0.042, 0.032$, and ${c}_{\phi }=0.003$, and are illustrated in Fig. 5. This allows us to capture the voltage-displacement behavior for the bending and torsional motions of the electrostatic actuator. Increasing the amplitude of the AC waveform from zero to ${\text{V}}_{\text{AC}}=52.15\text{ V}$, Fig. 6a, the in-plane bending motion gradually grows while the torsional motion remains trivial. Increasing AC voltage load further leads to the branching of the dynamic response under a primary Hopf bifurcation, resulting in the doubling of the period of the actuator's in-plane response. The 2:1 modal interaction between the in-plane bending and torsional motions initiates at this point. Amplifying the voltage beyond the bifurcation point, the amplitude of the stable bending motion reaches a nearly saturated state; however, the amplitude of the torsional motion starts to increase. The findings indicate that applying an AC voltage of 70 V induces in-plane motion with an amplitude less than 0.5 μm and torsional motion with 0.216 rad.

Fig. 6

The influence of the transverse viscous damping coefficient on the voltage-displacement behavior of the MEMS. The overall offset in position of the centroid of the beam's cross-section is assumed to be ${z}_{0}=0.035 h$, for $\Omega =1.0002$ and ${c}_{\phi }=0.003$. The left and right vertical axes refer to the black and brown curves, respectively, expressing the amplitudes of the plate's in-plane transverse and rotational displacements at the tip of the microbeam. The in-plane damping parameter is (a) ${c}_{w}=0.042$, and (b) ${c}_{w}=0.032$

This analysis demonstrates the efficiency of the proposed actuation mechanism using indirect excitation, channeling the vibration energy from the bending mode to the torsional mode. Figure 6b displays the voltage-displacement curve for ${c}_{w}=0.032$. It shows that reducing the damping parameter advances the onset of modal interaction, while maintaining the overall dynamics of the system unchanged.

Figure 7 explores the influence of the cross-sectional imperfection parameter, ${z}_{0}$, which introduces non-zero first moments of area for the suspension microbeams, subsequently, giving rise to quadratic nonlinear terms between the in-plane bending and torsional motions, on the MEMS voltage-displacement behavior. The AC frequency and the damping parameters are set to be as previous. The results reveal that increased symmetry, reduced imperfection, in the microbeam cross-section retards the development of energy exchange between the flexural and torsional motions of the microsuspensions. Reducing the z-component of the overall offset of the cross-sectional centroid from 3.5% to 2.5% of the microbeam's thickness delays the inception of modal interaction by about 20 V, Fig. 6a. The dashed lines in the figure represent the unstable periodic solutions where the two motions are not engaged. Those solutions correspond to the trivial unstable branches for the torsional motion as depicted in Fig. 7b.

Fig. 7

The influence of the overall offset in position of the centroid of the microbeam's cross-section on the voltage-displacement of the MEMS. The system's parameters are as follows: ${c}_{w}=0.042$, ${c}_{\phi }=0.003$, and $\Omega =1.0002$. (a) illustrates the amplitude of the in-plane transverse displacement at the microbeam's tip, for ${z}_{0}=0.035 h$ (black curve) and ${z}_{0}=0.025 h$ (blue curve). (b) depicts the amplitude of the plate's rotational motion, for ${z}_{0}=0.035 h$ (brown curve) and ${z}_{0}=0.025 h$ (blue curve)

In the following, we aim to demonstrate that the voltage value required for the activation of the 2:1 flexural–torsional modal interaction in the proposed electrostatic MEMS can be reduced substantially via exploiting electro-mechanical resonance syntonization. To this, the inductance of the electrical circuit is tuned so that the electrical resonant frequency of the RLC circuit is set to match with half of the natural frequency of the first in-plane bending mode of the mechanical structure. This amplifies the voltage amplitude across the MEMS capacitance while the system operates under unbiased waveforms. For unbiased voltage signals, AC frequency should be set to half of the natural frequency of a mechanical mode to directly excite this mode, $\Omega \approx \frac{1}{2}{\omega }_{b}^{1}$. Since because the electrical resonant frequency is also set at half of the natural frequency of the mechanical mode of interest, ${\omega }_{e}\approx \frac{1}{2}{\omega }_{b}^{1}$, the electrical charge circulating within the RLC circuit resonates due to the nearness of the supplied AC voltage's frequency to the electrical resonance, $\Omega \approx {\omega }_{e}$. The electrical charge resonance results in an amplification of voltage observed across the MEMS capacitance, thereby intensifying the electrostatic force applied to the microstructure. It is worth noting that the electrostatic force and torque are at $2\Omega \approx {\omega }_{b}^{1}$. So, the electrostatic field amplification leads to an amplification in the system's response (bending motion) happening at $2\Omega$. Up to this point, the MEMS has undergone a 1:2 electro-mechanical modal interaction, where the electrical mode is directly excited using an unbiased voltage signal, and the mechanical (flexural) motion is indirectly excited through an energy channel formed by the quadratic nonlinearity associated with electrical charge present in the dynamics of the mechanical side. This channel supplies an auto-parametric excitation for the mechanical motion, occurring at twice the AC frequency. On the other hand, the bending motion resonates because the electrostatic force frequency is located near the natural frequency of the first in-plane flexural mode. This implies that there are two factors contributing to the amplification of the mechanical in-plane bending motion: one is due to resonance in the applied electrostatic force intensity, and the other is due to the proximity of the electrostatic force frequency to the mechanical mode's natural frequency. This technique enables us to effectively bridge the in-plane flexural motion of the microbeams to their torsional motion via supplying lower voltages. Conclusively, the proposed actuation technique for electrostatic MEMS actuators features 1:2:1 electro-flexural–torsional (one electrical mode incorporated with two mechanical modes) modal interactions upon activating the energy channel between the bending and torsional motions of the movable electrode.

The steady-state dynamics of the MEMS actuator in the presence of electro-mechanical resonance syntonization is illustrated in Fig. 8. Here, the system's parameters are as follows: ${z}_{0}=0.035 h$, ${c}_{w}=0.042$, ${c}_{\phi }=0.003$, ${\text{V}}_{\text{AC}}=10\text{ V}$. The bending motion is characterized by a butterfly-shaped frequency-displacement curve, in which the left and right peaks of the curve are formed by the electrical and mechanical bending modes, respectively. The V-shaped stable branch features the flexural–torsional modal interaction. Sweeping the AC frequency from below half of the bending mode's natural frequency, the in-plane motion grows without the presence of torsional motion. This trend persists until the MEMS dynamics meet a cyclic-fold bifurcation (CF₁) at $2\Omega =1.8809$, leading to instability in the response. Turning the sweep direction at this point, the system's dynamics develop along an unstable large-amplitude periodic orbit for the bending motion, whereas the torsional mode still remains trivial. Continuing this solution branch leads the system to experience the second cyclic-fold bifurcation (CF₂) happening at $2\Omega =1.7877$, forming the left peak of the M-shaped curve. Turning the sweep direction from backward to forward enables the capture of the large-amplitude periodic response for the in-plane transverse motion. Moving along this branch, the amplitude of the bending motion decreases gradually via increasing the AC frequency until the forcing frequency reaches $2\Omega =1.9918$. At this point, the dynamics of the electro-flexural system undergo a secondary Hopf bifurcation, denoted by S-HP₁, provided that the periodic motions become unstable. Increasing the AC frequency further propels the MEMS into a quasi-periodic regime that is incorporated with only the electrical and flexural modes. However, the frequency interval associated with this behavior is extremely narrow so that slightly growing the sweeping parameter causes the system's response to exhibit branching under a period-doubling bifurcation (PD₁) at $2\Omega =1.9935$. It is worth noting that there is no stable periodic orbit co-existing with the quasi-periodic response within this frequency range, between S-HP₁ and PD₁. The initiation of torsional motion along the unstable non-trivial branch is observed in Fig. 8b when the forcing frequency surpasses PD₁. It should be noted that the solutions obtained along the V-shaped branch for the bending (shown in Fig. 8a), and the reversed V-shaped branch for the torsional and electrical motions (shown in Fig. 8b and c), are outcomes of a 1:2:1 electro-flexural–torsional modal interactions happening in the dynamics of the electrostatic MEMS actuator. Continuing along this branch, the amplitude of the in-plane transverse motion starts to decrease, while correspondingly, the torsional motion grows rapidly until the steady-state response undergoes the second secondary Hopf bifurcation, as denoted by S-HP₂ at $2\Omega =1.9936$, recovering stability in the response. Further increasing the parameter, the bending motion amplitude drops to a minimum, while the plate's rotation angle reaches its maximum at $2\Omega =1.9984$. Beyond this frequency, the torsional motion initiates a reduction once again until the stability of the MEMS dynamics is lost under the third secondary Hopf bifurcation, S-HP₃, at $2\Omega =2.0051$. Continuing the parameter sweep beyond this point, the dynamic response transitions to a quasi-periodic regime involving all three modes, electrical, flexural, and torsional. This situation resembles the behavior observed at the beginning of constructing this solution branch. This behavior extends until the unstable non-trivial solutions to the torsional motion merge its unstable trivial solutions under a reversed period-doubling (PD₂) bifurcation at $2\Omega =2.0059$. Further increasing the AC frequency, the torsional motion remains vanishing; however, the unstable electrical and bending periodic motions retrieve their stability along the large-amplitude branch under the fourth secondary Hopf (S-HP₄) bifurcation occurring at $2\Omega =2.0381$.

Fig. 8

The steady-state dynamics of the MEMS in the presence of electro-mechanical resonance syntonization, for ${z}_{0}=0.035 h$, ${c}_{w}=0.042$, ${c}_{\phi }=0.003$, ${\text{V}}_{\text{AC}}=10\text{ V}$. Here, the electrical resonant frequency is located at half of the natural frequency of the first in-plane bending mode, ${\omega }_{e}=\frac{1}{2}{\omega }_{b}^{1}$, introducing a 1:2 modal interaction between the electrical and mechanical/bending modes of the MEMS. (a), (b), and (c) depict the frequency–response curves for the plate's transverse and rotational motions and the electrical current, respectively

Driving the electrostatic MEMS using an unbiased AC waveform with amplitude of ${\text{V}}_{\text{AC}}=15\text{ V}$ keeping the cross-sectional imperfection and damping parameters identical to the previous case, provides the system with richer dynamics, Fig. 9. The overall steady-state behavior of the actuator is similar to what was presented in Fig. 8; however, the main distinctions are as the following: 1) the second cyclic-fold bifurcation forming the left peak of the M-shaped frequency–response curve for the bending motion (shown in Fig. 8) disappears in Fig. 8, and instead, the large-amplitude unstable solution branch continues until dynamic pull-in occurs. In addition, the large-amplitude stable motions near pull-in undergo a primary Hopf bifurcation (HP₃) at $2\Omega =1.4403$. 2) Traversing the stable large-amplitude solution branch and extending the forcing frequency beyond the right peak of the M-shaped curve lead to the consecutive occurrence of two primary Hopf bifurcations, HP₁ and HP₂, where the former introduces instability, while the later restores stability in the system dynamics. Upon comparing Figs. 8 and 9, a noteworthy finding is that, despite a 5 V-increase in AC voltage leads to a roughly 0.3 μm growth in the large-amplitude transverse motion, the amplitude of the local minima for the in-plane bending motion, observed within the frequency range activating electro-flexural–torsional modal interactions, remains nearly constant. This implies saturation in the in-plane motion and enhancement in the rotation of the microbeam's tip.

Fig. 9

The steady-state dynamics of the MEMS in the presence of electro-mechanical resonance syntonization, for ${z}_{0}=0.035 h$, ${c}_{w}=0.042$, ${c}_{\phi }=0.003$, ${\text{V}}_{\text{AC}}=15\text{ V}$. The electrical resonant frequency is adjusted at half of the shifted natural frequency of the first in-plane bending mode, ${\omega }_{e}=\frac{1}{2}{\omega }_{b}^{1}$. (a) illustrate the frequency–response curve for the in-plane bending motion of the microbeam's tip, and (b) depicts the frequency-rotational displacement curve for the rigid plate

Figure 10 illustrates the voltage-response behaviors of the electrostatic MEMS while the electrical resonant frequency is syntonized with half of the natural frequency of the first in-plane bending mode, for ${z}_{0}=0.035 h$ and ${z}_{0}=0.025 h$. The AC frequency is freezed at $\Omega =1.0002$, and the damping parameters are set to be ${c}_{w}=0.042$ and ${c}_{\phi }=0.003$. Figure 9a depicts that the periodic orbits associated with the transverse motion extends in amplitude as the applied AC voltage signal intensifies. For the overall offset of 3.5% of the microbeam's thickness in the z-component of the cross-sectional centroid, the MEMS's dynamics loses its stability at ${\text{V}}_{\text{AC}}=3.53\text{ V}$ through secondary Hopf bifurcation, as a result of the 1:2:1 electro-flexural–torsional modal interactions (black curve in Fig. 10a). This triggers the plate's rotational motion accompanied by a period-doubling bifurcation in the structure's in-plane transverse motion. However, for ${z}_{0}=0.025 h$, growth in the in-plane bending motion, without the involvement of the torsional mode, extends until the AC voltage amplitude reaches 8.1 V. Up to this point, the MEMS operates under 1:2 internal resonance between its electrical and bending modes. Further increasing the waveform amplitude propels the system into instability through a secondary Hopf bifurcation, S-HP₁, at this AC voltage. It is important to note that this bifurcation is contributed solely by the electrical and the bending modes of the MEMS. Keep forward sweeping the parameter up to ${\text{V}}_{\text{AC}}=8.58\text{ V}$ results in growth and decrease in the amplitudes of the in-plane bending motion and electrical current, respectively. Raising the voltage amplitude beyond 8.58 V results in the appearance of a co-existing unstable solution branch, identified by a doubling of the period in the in-plane bending motion. The period-doubling bifurcation is the result of the torsional mode engagement. The MEMS actuator operates under the 1:2:1 electro-flexural–torsional modal interactions while moving along this unstable branch. Further increasing the voltage amplitude allows the system to retrieve its stability through a reversed secondary Hopf bifurcation, S-HP₂, at ${\text{V}}_{\text{AC}}=8.65\text{ V}$. In contrast to the scenario where the electrical mode is not engaged, the system's torsional mode is triggered at voltages one-tenth of the amplitude required to initiate the 2:1 modal interaction between the structure's in-plane bending and torsional motions. As seen, we can indirectly drive the plate's rotational motion through forming an energy channel that transfers the vibration energy from the in-plane bending motion to the torsional motion supplying 3.53 V in the presence of electro-mechanical resonance syntonization. This highlights the efficiency of the proposed actuation mechanism that eliminates the need for electrodes underneath the plate to induce out-of-plane rotations. Similar to the previous results presented in Fig. 7, the smaller the imperfection parameter, the higher the voltage required to initiate the modal interaction. Moreover, moving along the stable non-trivial branch for torsional motion is accompanied by a gradual increase in the in-plane bending displacement with a small slope. Here, the in-plane motion almost saturates. However, it is noteworthy that the microstructure does not travel more than one-third of the in-plane capacitive gap when the plate rotates out-of-plane with an angle of about 0.3 rad, achieved by applying 15 V for ${z}_{0}=0.025 h$, Fig. 10b. The electrical current flowing through the RLC circuit, depicted in Fig. 10c, includes information about the in-plane bending and torsional motions. Therefore, it can be effectively utilized to capture the 1:2:1 electro-flexural–torsional modal interactions via implementing a motion-induced current measurement method. This issue will be addressed in our future study in detail.

Fig. 10

The voltage-displacement behaviors of the electrostatic MEMS in the presence of electro-mechanical resonance syntonization, for two different values of the cross-sectional imperfection parameter, ${z}_{0}=0.035 h$ and ${z}_{0}=0.025 h$. The AC frequency is freezed at $\Omega =1.0002$, and the viscous damping parameters are assumed to be ${c}_{w}=0.042$ and ${c}_{\phi }=0.003$. (a), (b), and (c) display the voltage-response curves for the plate's in-plane transverse and rotational displacements and the electrical current circulating through the RLC circuit, respectively

4.2 Electro-flexural–torsional modal interactions: Quasiperiodicicity

The time evolution for the in-plane bending and torsional motions of the movable electrode is displayed in Fig. 11, for ${z}_{0}=0.035 h$, ${c}_{w}=0.042$, ${c}_{\phi }=0.003$, and ${\text{V}}_{\text{AC}}=88\text{ V}$. These responses correspond to the frequency–response curves presented in Fig. 3a and b. Here, the AC frequency is set to linearly vary near half of the first bending mode's natural frequency with a sweep rate of $1\times {10}^{-7}$ (non-dimensional frequency per non-dimensional time). It is important to note that, in order to avoid significant reduction in the numerical integration tolerances, we scale up the time variable via non-dimensionalizing it with respect to the first torsional natural frequency of the structure. However, the MEMS's time histories are plotted over the dimensional time. In the figure, the profiles of the time evolutions reflect the frequency-displacement curves presented in Fig. 3a and b. The MEMS motion begins with periodic in-plane bending oscillations and the amplitude of the steady-state response gradually grows as the AC frequency is swept forward, and correspondingly, the torsional mode of the movable electrode remains vanishing. This behavior trends until reaching the instant $t=0.8 s$. Beyond this point, the structure's torsional motion is triggered, and the MEMS's dynamics route to a quasi-periodic regime, as indicated by beating responses in its time envelopes, and once again transition to periodicity at $t=0.9 s$, as the AC frequency is increased further. Those windows are marked by dashed yellow rectangles in Fig. 11a and c, and their zoomed views are illustrated in Fig. 11b and d, for the bending and torsional motions, respectively. The frequency content of the system's responses at three different regimes, points A, B, and C, are calculated by taking Fast Fourier Transformation (FFT) of the MEMS's time-domain response. Figure 11e and d confirm the in-plane transverse motion contains only a single harmonic at the forcing frequency, and the plate's out-of-plane rotation angle is trivial, while the MEMS is set to operate at point A (before the initiation of the 2:1 modal interaction). Nevertheless, at point C, the torsional motion is non-trivial, owing to the 2:1 flexural–torsional modal engagement, and oscillates with a frequency that equals half of the forcing frequency, $\frac{1}{2}{\omega }_{f}=\Omega$, and simultaneously, the bending motion maintains the harmonic at the forcing frequency and its amplitude becomes minimized. This is shown in Fig. 11g and h. The FFTs of the MEMS's bending and torsional motions at instant B are individually depicted in Figs. 12a and 13a, respectively.

Fig. 11

Time histories of the MEMS's motions, and FFT diagrams of the steady-state dynamic response of the system, for ${z}_{0}=0.035 h$, ${c}_{w}=0.042$, ${c}_{\phi }=0.003$, and ${\text{V}}_{\text{AC}}=88\text{ V}$. (a) and (c) depict the temporal envelope for the in-plane bending and torsional motions, respectively. The dashed yellow rectangles embed the regions where the responses exhibit beating, and their zoomed views are shown in (b) and (d) for the bending and torsional displacements, respectively. FFT plots of the transverse motion of the microbeam's tip are shown in (e) and (g), while (f) and (h) illustrate the FFT plots of the plate's rotational displacement

Fig. 12

(a) The frequency content of the plate's in-plane motion for $\Omega =0.996$ that corresponds to point B shown in Fig. 11b. The values of the damping coefficients, imperfection parameter, and the AC voltage are similar to those assumed in Fig. 11. The first harmonic is at the forcing frequency, ${\omega }_{f}=2\Omega =1.992$. The FFT diagram in the vicinity of each harmonic is magnified and displayed in (b), (c), (d), (e), (f), and (g), demonstrating the generation of localized frequency combs with a frequency spacing of $\delta \omega =\frac{{\omega }_{f}}{449}=0.0044$

Fig. 13

(a) The frequency content of the plate's rotational motion for $\Omega =0.996$ that corresponds to point B shown in Fig. 11b. The system's parameters are consistent with those assumed in Fig. 11. The first harmonic is at half of the forcing frequency, $\frac{1}{2}{\omega }_{f}=\Omega =0.966$. The FFT diagram in the vicinity of each harmonic is zoomed and shown in (b), (c), (d), (e), (f), and (g), demonstrating the formation of localized frequency combs with a frequency spacing of $\delta \omega =\frac{{\omega }_{f}}{449}=0.0044$

The frequency-domain representation in Fig. 12a depicts the dynamic response of the suspension microbeams with a mid-span plate oscillating at the AC frequency ($\Omega =0.9960$) corresponding to point B in the response shown in Fig. 11a. The FFT amplitude is plotted in dB scale versus non-dimensional frequency. The in-plane displacement of the microbeam's tip includes a harmonic at the forcing frequency, as a fundamental harmonic, together with extra five harmonics appearing at integer multiples of the forcing frequency within the frequency interval from 0 to 13. Each peak is symmetrically surrounded by equally spaced teeth generating localized frequency combs. These combs emerge due to the occurrence of a secondary Hopf bifurcation incorporated by the bending and torsional motions. For instance, inspecting the FFT plot in the vicinity of the first harmonic, we observe that there are 23 teeth generated on either side of the centered peak, Fig. 12b. Those small peaks are equidistant with a frequency spacing of $\delta \omega =\frac{{\omega }_{f}}{449}=0.0044$. Contrasting Fig. 12b and c, the density of the produced frequency combs decreases as we move from the first harmonic to the second one. The count of teeth appearing on either side of the second harmonic is nine. This pattern remains nearly identical for the combs formed around the third harmonic. However, as we shift to the fourth harmonic, the density of the combs increases once more, reaching 26 equidistant small peaks distributed on either side of the centered peak. On the contrary, the frequency combs generated around the fifth harmonic extend over a narrower frequency span compared to those around the fourth harmonic. Magnifying the frequency-domain response near the sixth harmonic reveals the formation of a frequency comb having 13 effective teeth on either side of the centered peak. This examination indicates that the proposed electrostatic MEMS actuator is also well-suited for producing localized frequency combs repeating at integer multiples of the forcing frequency. The frequency content of the torsional motion, corresponding to point B in the response illustrated in Fig. 11d, demonstrate denser frequency combs localized around half of the forcing frequency ($\frac{1}{2}{\omega }_{f}$) and its odd integer multiples up to 11 times the forcing frequency, Fig. 13a. Zooming the FFT diagram in the vicinity of the fundamental peak reveals the generation of a local frequency comb with 32 teeth on either side of the centered frequency. Unlike the bending motion, the teeth density remains almost unchanged as moving to the frequency combs localized around the higher-order harmonics. It is important to mention that the frequency spacing is equal to that of the in-plane bending motion.

Moreover, the results demonstrate the capability to construct a compound readout signal in the frequency domain via combining the frequency spectra of the two resonators, namely the bending and torsional motions. This allows for the generation of a more extensive frequency comb using quasi-periodicity that spans a continuous frequency range.

Figure 14 illustrates the time histories for the transverse displacement and electrical current of the MEMS in the presence of electro-mechanical resonance syntonization, 1:2:1 modal interactions between the electrical, flexural, and the torsional modes. Here, the system's parameters are as follows: ${z}_{0}=0.035 h$, ${c}_{w}=0.042$, ${c}_{\phi }=0.003$, and ${\text{V}}_{\text{AC}}=10\text{ V}$. The temporal profiles correspond to the frequency–response curves illustrated in Fig. 8. The MEMS's motion commences with small-amplitude periodic oscillations around its shifted equilibrium position as the AC frequency grows linearly with the sweep rate same as previous. The response jumps up to the large-amplitude envelope at $t=0.256 s$. As the time goes on, the amplitudes of the in-plane bending motion and electrical current reduce along the large-amplitude periodic orbits, and eventually, the MEMS's dynamics route to a quasi-periodic regime at $t=0.713 s$, Fig. 14a and c. This behavior does not linger and the system retrieves periodicity as approaching $t=0.861 s$. The dashed yellow and red rectangles in the figures capture the responses within the windows limited by the first and fourth secondary Hopf bifurcations shown in Fig. 8a and c. These windows encompass the transient quasi-periodic response that is a result of the 2:1 bending-torsional modal interaction, and the steady-state quasi-periodic response that arises from a 1:2 electro-mechanical/bending modal interaction. The transitions from the former quasi-periodicity to the later one is more obvious in the time evolution of the electrical current. In Fig. 13b and d, the time envelopes exhibit equidistant sharp peaks distributed throughout the quasi-periodic regime, forming time-domain combs. For a certain AC frequency within this window, $\Omega =1.0002$, time histories for the in-plane displacement of the microbeam's tip, plate's rotation angle, and the electrical current passing across the capacitance, are shown in Fig. 15a, c, and e, respectively. Correspondingly, their FFT plots are computed and depicted in Fig. 14b, d, and f. Here, the system is released from its rested configuration. It is demonstrated that the MEMS's dynamics evolve along quasi-periodic orbits in its transient response; however, the steady-state responses settle into periodic orbits formed via energy exchange between the bending and torsional motions.

Fig. 14

Time history of the electrostatic MEMS with electro-mechanical resonance syntonization. The simulated time envelopes correspond to the frequency–response curves presented in Figs. 8a and c. (a) and (c) depict the time histories for the plate's in-plane motion and the electrical current, respectively. The dashed rectangles indicate the regions where the MEMS's dynamics undergo quasi-periodicity, generating combs in the time-domain, and their zoomed views are illustrated in (b) and (d)

Fig. 15

Time histories for the plate's in-plane transverse and out-of-plane rotational displacements, and the electrical current, for $\Omega =1.0002$, are shown in (a), (c), and (e), respectively. The system's parameters are equal to those presented in the caption of Fig. 8. The FFT plots for (a), (c), and (e) are shown in (b), (d), and (f), respectively, indicating the manifestation of a period-doubling bifurcation in the MEMS's response upon the initiation of the 2:1 mode engagement between the in-plane and torsional motions

Referring to Fig. 15a and c, the transition from quasi-periodicity to periodicity in the in-plane flexural displacement is synchronized with gradual enlargements in the amplitude of the torsional motion. The 2:1 internal resonance channel leads to a reduction and saturation in the amplitude of the in-plane motion, while simultaneously driving the torsional motion to grow up to a maximum, depending on the input voltage amplitude. This phenomenon is characterized by the occurrence of period-doubling bifurcation, Fig. 15b and d. Furthermore, the electrical current's transient dynamics feature a more interesting response as compared to that of the in-plane displacement, Fig. 15e. The equidistant sharp teeth emerging in the quasi-periodic regime introduce time-domain combs. Also, the figure illustrates that the electrical current amplifies when the torsional motion initiates, contributing to the effective capacitance defined between the movable and stationary electrodes. These results indicate that the proposed electrostatic MEMS actuator, operating on the principle of 1:2:1 electro-flexural–torsional modal interactions, is well-suited for the application of periodic out-of-plane rotation drives and quasi-periodic-based time- and frequency-domain combs generated from both the transient and steady-state dynamics of the MEMS.

Tuning the AC frequency to locate the MEMS's dynamics within the frequency interval limited by the second period-doubling (PD₂) and the fourth secondary Hopf (S-HP₄) bifurcations, where the torsional motion lies on the unstable trivial branch, leads the actuator to operate under quasi-periodicity in its steady-state, Fig. 8. Here, the AC frequency is set at $\Omega =1.005$. Unlike the results presented in Fig. 15, the frequency combs observed here arise from a 1:2 modal interaction happening between the electrical and mechanical/bending modes of the MEMS. The FFT diagram of the electrical current flowing through the RLC circuit is depicted in Fig. 15a. The result exihibts the formation of five combs within the shown non-dimensional frequency range. The first comb is centered around the AC frequency containing 12 equally spaced teeth on either side. As seen, the base profiles of the teeth for the first two combs, located at and three times the AC frequency, follow a Lorentzian-type curve. Moving to higher frequencies, the signal power drops, leading to the disappearance of this curve. The magnified views of the frequency combs are shown in Fig. 16b–e. As compared to the unsyntonized electro-mechanical resonance case, the frequency spacing of the combs has increased, $\delta \omega =\frac{\Omega }{21.62}$, with enhanced symmetry in the amplitudes of the teeth surrounding the center frequencies. Moreover, the number of teeth remains almost consistent while transitioning from one set of frequency combs to another.

Fig. 16

The FFT diagram of the MEMS's electrical current in the presence of electro-mechanical resonance syntonization, for $\Omega =1.005$. The system's parameters are equal to those presented in the caption of Fig. 7. The operating frequency is located between the second period-doubling (PD₂) and the fourth secondary Hopf (S-HP₄) bifurcations shown in Fig. 8a. The zoomed view for the frequency combs localized around the first four harmonics appearing at $\frac{1}{2}{\omega }_{f}$, $\frac{3}{2}{\omega }_{f}$, $\frac{5}{2}{\omega }_{f}$, and $\frac{7}{2}{\omega }_{f}$ are shown in (b), (c), (d), and (e), respectively

It is worth noting that the stability of the frequency combs generated, as a result of secondary Hopf bifurcations in coupled resonators, can be easily compromised. This is because small disturbances in the systems' parameters, such as the forcing frequency, can lead to a transition from quasi-periodicity to a periodic regime, causing the combs to vanish. With this in mind, a robust and nonlinear control mechanism is required to maintain the system's dynamics at a desired operating condition, generating reliable frequency combs. This subject will be studied in our upcoming work. Further, our experimental studies realizing indirect excitation technique based on flexural–torsional modal interaction are still ongoing and will be released in future.

5 Concluding remarks

In this study, we proposed an electrostatic MEMS actuator for out-of-plane rotation drive based on indirect excitation, in symmetrically designed microstructures with minuscule cross-sectional asymmetry. A MEMS structure was designed to feature a 2:1 commensurate ratio between its first in-plane bending and first torsional modes. The proposed method suggests to indirectly drive the structure's torsional motion via directly exciting the in-plane bending mode and auto-parametrically transferring the vibration energy from the in-plane motion to the out-of-plane torsional motion of the structure. The study uncovers, never explored before, that a minuscule imperfection induced in the cross-section of the suspension microbeams sources quadratic structural nonlinearities required for the initiation of a 2:1 internal resonance between the in-plane flexural and torsional motions. This imperfection signifies the deviation between the bending NA of the as-fabricated microbeam and torsional center of the actual cross-section. This modification enables the current beam-based mathematical models to capture a 2:1 modal interaction between flexural and torsional modes in symmetrically designed structures. The results indicate that as the imperfection approaches vanishing, bringing the position of the centroid of the actual cross-section closer to that of the ideal one, the onset of the modal interaction is delayed beyond the pull-in voltage. The efficiency of the proposed method was demonstrated via numerically examining the frequency- and voltage-displacement behaviors of the MEMS actuator. The findings show that the steady-state dynamics of the in-plane motion is characterized with M-shaped frequency–response curves, including secondary Hopf bifurcations along the IR-branch. Furthermore, the in-plane bending motion can be efficiently minimized by appropriately tuning the AC frequency once the mode engagement is triggered. Interestingly, the largest torsional motion is achieved at the forcing frequency where the bending motion amplitude is minimized. In addition, the voltage-displacement behavior demonstrates saturation in the amplitude of the high-frequency and directly excited mode, the in-plane bending motion. In addition, the study's results show that syntonizing the electrical resonant frequency to the natural frequency of the first in-plane flexural mode substantially reduces the activation level of the bending-torsional modal interaction. This was implemented under the employment of a 1:2:1 electro-flexural–torsional internal resonance. Eventually, we showed that the proposed electrostatic MEMS is also well-suited for generating frequency- and time-domain combs rooted in both transient and steady-state dynamics of the MEMS, featuring quasi-periodic characteristics. The results indicate that in the presence of electro-mechanical resonance syntonization, the localized combs exhibit a reduced number of teeth, an increased frequency spacing, and enhanced power as compared to the unmatched case.

In the context of utilizing frequency and time combs in various applications such as, quantum computing [89, 90], precise measurements [91, 92], telecommunications [93, 94], spectroscopy [95, 96], etc., ensuring the stability of frequency combs derived from periodic or quasi-periodic dynamics is of utmost importance. Practically speaking, proposing a technique for generating phononic frequency combs via driving an electrostatic MEMS within the quasi-periodic regime, oscillating between two secondary Hopf/Neimark-Sacker bifurcations on a large-amplitude response branch, without formulating a control mechanism, is simply unfeasible and unrealistic. With this in mind, we aim to control the dynamics of our proposed MEMS actuator through implementing a nonlinear control mechanism allowing us to introduce robust quasi-periodic responses.

Appendices

Appendices

Appendix A: Non-vanishing first moment of area

Figure 

Fig. 17

The microbeam's cross-section includes imperfection. The gray rectangular area with perfect edges shows the ideal cross-section. The scattered red curves perturbed around the perfect edges indicate the edges of the actual cross-section

17 illustrates the cross-section of a microbeam at a position s measured from the origin $O$. The figure shows slight offsets randomly distributed along the ideal (as-designed) cross-sectional edges, resulting from fabrication imperfections, leading to a tiny deviation in the positions of the ideal C and the actual C. Here, ${y}_{0}(s)$ and ${z}_{0}(s)$, respectively, denote the y- and z-coordinates of the actual C. To uncover the quadratic nonlinear terms that couple the bending and torsional motions of the microbeam, it is sufficient to calculate the following integrals over the realistic (as-fabricated) cross-sectional area when formulating the equations of motion. Observe that.

$$ \begin{gathered} Q_{yy} = \mathop {\iint }\limits_{{A_{actual} }} zdA = A_{actual} \left( s \right)z_{0} \left( s \right) \ne 0, \hfill \\ Q_{zz} = \mathop {\iint }\limits_{{A_{actual} }} ydA = A_{actual} \left( s \right)y_{0} \left( s \right) \ne 0, \hfill \\ \end{gathered} $$

(A.1)

where, ${Q}_{yy}$ and ${Q}_{zz}$ denote the first moments of area of the actual cross-sections, with respect to the y- and z-axes, respectively. It is important to note that these two quantities are present in the coefficients of quadratic stiffness term in the beam equations, which can be identified through experiments. As per the microdevice fabrication handbook [97], there is an approximate tolerance of 5–10% allowed for as-designed feature sizes, which encompasses imperfections resulting in minor asymmetries in structures originally designed to be symmetrical.

Appendix B: Mathematical model

The origin of the global Lagrangian coordinate system, $OXYZ$ with the unit vectors ${\mathbf{i}}_{a}$,${\mathbf{i}}_{b}$, and${\mathbf{i}}_{c}$, is positioned at the centroid of the left end's cross-section, having X-axis aligned with the middle axis of the microbeams, Fig. 

Fig. 18

(a) Schematic showing a portion of the microbeam suspension together with the beam element. (b) Three successive Euler angles introducing the orientation of the beam's cross-section

18a. The $ABCD$ plane depicts the microbeam's cross-section at a distance $s$ from the origin$O$. The beam element in its undeformed configuration extends out of this plane in the positive direction of the X-axis with a length of$ds$. $oxyz$ introduces a Lagrangian coordinate system, with the unit vectors ${\mathbf{i}}_{x}$,${\mathbf{i}}_{y}$, and${\mathbf{i}}_{z}$, which is locally attached to $ABCD$ plane in its undeformed configuration. $\overrightarrow{\mathbf{D}}$ denotes the translational displacement vector of the centroid of the $ABCD$ plane.

The variables${u}_{i}(s;t)$,${v}_{i}(s;t)$, and ${w}_{i}(s;t)$ represent the x-, y-, and z-components of the displacement vector$\overrightarrow{\mathbf{D}}$. According to the figure, the origin $o$ is placed at a material point located on the beams' NA at a position $s$ measured from the origin$O$. The variables${\psi }_{i}(s;t)$,${\theta }_{i}(s;t)$, and ${\phi }_{i}(s;t)$ represent the Euler angles associated with the three successive rigid body rotations of the microbeam's cross-section. These rotations occur around the $z$-axis, followed by the ${y}^{\prime}$-axis, and finally, the ${x}^{{\prime}{\prime}}$-axis, Fig. 18b. $o\zeta \eta \xi$ with the unit vectors ${\mathbf{i}}_{1}$,${\mathbf{i}}_{2}$, and ${\mathbf{i}}_{3}$ refers to the coordinate system local to the beam's cross-section in deformed configuration [73]. This approach captures the nonlinear curvatures of the beam's middle axis in the deformed configuration. However, it overlooks the slope of the beam's middle axis due to the assumption of clamping for the face of the beam element placed on the $\eta \xi$-plane. In the following, we show the incorporation of the middle axis's slope into the strain potential energy via setting the local displacement field at the $oxyz$ coordinate system in the undeformed configuration.

B.1 Kinetic energy

In this study, we are interested in analyzing the coupling between the symmetric in-plane bending, $w$, and out-of-plane rotational, $\phi$, motions of the actuator. Therefore, we focus on the half of the structure and neglect the out-of-plane transverse displacement, $v\left(s;t\right)=0$.

The position vector of material particle P on the $\eta \xi$-plane is expressed as follows.

$${\overrightarrow{\mathbf{r}}}_{\mathbf{p}}=s {\mathbf{i}}_{\text{a}}+u\left(s;t\right){\mathbf{i}}_{\text{x}}+w\left(s;t\right){\mathbf{i}}_{\text{z}}+y {\mathbf{i}}_{2}+z {\mathbf{i}}_{3} ; ({\mathbf{i}}_{\text{a}}={\mathbf{i}}_{\text{x}} , {\mathbf{i}}_{\text{b}}={\mathbf{i}}_{\text{y}} , {\mathbf{i}}_{\text{c}}={\mathbf{i}}_{\text{z}})$$

(A.2)

The transformation matrix, $[\mathbf{T}]$, between ${\mathbf{i}}_{\text{x}},{\mathbf{i}}_{\text{y}},{\mathbf{i}}_{\text{z}}$ and ${\mathbf{i}}_{1},{\mathbf{i}}_{2},{\mathbf{i}}_{3}$ orientations are given by

$$ \begin{gathered} \left\{ {\begin{array}{*{20}c} {{\mathbf{i}}_{1} } \\ {{\mathbf{i}}_{2} } \\ {{\mathbf{i}}_{3} } \\ \end{array} } \right\} = \left[ {\mathbf{T}} \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{i}}_{x} } \\ {{\mathbf{i}}_{y} } \\ {{\mathbf{i}}_{z} } \\ \end{array} } \right\}, \hfill \\ \left[ {\mathbf{T}} \right] = \left[ {\begin{array}{*{20}c} {\cos \theta } & 0 & { - \sin \theta } \\ {\sin \phi \sin \theta } & {\cos \phi } & {\sin \phi \cos \theta } \\ {\cos \phi \sin \theta } & { - \sin \phi } & {\cos \phi \cos \theta } \\ \end{array} } \right] \hfill \\ \end{gathered} $$

(A.3)

The Euler angle, $\theta$, can be found in terms of the displacement of the origin of the $oxyz$ coordinate system, $u$ and $w$, and it reads

$$\theta ={\text{tan}}^{-1}\left(\frac{-{w}^{\prime}}{1+{u}^{\prime}}\right)\approx -{w}^{\prime}+{u}^{\prime}{w}^{\prime}-{{u}^{\prime}}^{2}{w}^{\prime}+\frac{1}{3}{{w}^{\prime}}^{3}+H.O.T$$

(A.4)

The angular velocity of the beam's cross-section placed on $ABCD$ plane is expressed with respect to $\zeta \eta \xi$ coordinate system, as follows

$$ \begin{gathered} \vec{\omega } = \theta ~{\mathbf{i}}_{{{\text{y}^{{\prime}}}}} + \phi ~{\mathbf{i}}_{{{\text{x}^{{\prime\prime}}}}} = \omega _{1} {\mathbf{i}}_{1} + \omega _{2} {\mathbf{i}}_{2} + \omega _{3} {\mathbf{i}}_{3} \hfill \\ \omega _{1} = \dot{\phi }\quad,\quad~\omega _{2} = \dot{\theta }\cos \phi ~,\quad~\omega _{3} = - \dot{\theta }\sin \phi \hfill \\ \end{gathered} $$

(A.5)

The velocity of particle P is found by taking derivative from Eq. (A.2) with respect to time:

$${\dot{\overrightarrow{\mathbf{r}}}}_{\mathbf{P}}=\left(\dot{u}+{T}_{11}\left(z{\omega }_{2}-y{\omega }_{3}\right)-z{\omega }_{1}{T}_{21}+y{\omega }_{1}{T}_{31}\right) {\mathbf{i}}_{\text{x}}+\left({T}_{12}\left(z{\omega }_{2}-y{\omega }_{3}\right)-z{\omega }_{1}{T}_{22}+y{\omega }_{1}{T}_{32}\right) {\mathbf{i}}_{\text{y}}+\left(\dot{w}+{T}_{13}\left(z{\omega }_{2}-y{\omega }_{3}\right)-z{\omega }_{1}{T}_{23}+y{\omega }_{1}{T}_{33}\right) {\mathbf{i}}_{\text{z}}$$

(A.6)

The kinetic energy of the microbeam is the integration of the kinetic energy of all material particles distributed over the volume $\Omega$, and it takes the following form

$${T}_{K}=\frac{1}{2}{\smallint }_{\Omega }\rho \left({\dot{\overrightarrow{\mathbf{r}}}}_{\mathbf{P}} .{\dot{\overrightarrow{\mathbf{r}}}}_{\mathbf{P}}\right)dV$$

(A.7)

Further, the position vector of the mass center of the half-plate, ${\overrightarrow{\mathbf{r}}}_{\mathbf{c}}$, is expressed in terms of the displacement components of the microbeam tip:

$${\overrightarrow{\mathbf{r}}}_{\mathbf{c}}=L {\mathbf{i}}_{\text{x}}+u\left(L;t\right){\mathbf{i}}_{\text{x}}+w\left(L;t\right){\mathbf{i}}_{\text{z}}+\frac{{l}_{p}}{4} {\mathbf{i}}_{1}\left(L;t\right)={\left.\left(u+\frac{{l}_{p}}{4}{T}_{11}\right)\right|}_{s=L} {\mathbf{i}}_{\text{x}}+{\left.\left(\frac{{l}_{p}}{4}{T}_{12}\right)\right|}_{s=L} {\mathbf{i}}_{y}+{\left.\left(w+\frac{{l}_{p}}{4}{T}_{13}\right)\right|}_{s=L} {\mathbf{i}}_{z}$$

(A.8)

The translational kinetic energy of the half-plate is written as

$${T}_{{K}_{P}}^{tr}=\frac{1}{2}\frac{{M}_{p}}{2}\left({\dot{\overrightarrow{\mathbf{r}}}}_{c} . {\dot{\overrightarrow{\mathbf{r}}}}_{c}\right)=\frac{{M}_{p}}{4}{\left[{\left(\dot{u}+\frac{{l}_{p}}{4}{\dot{T}}_{11}\right)}^{2}+{\left(\frac{{l}_{p}}{4}{\dot{T}}_{12}\right)}^{2}+{\left(\dot{w}+\frac{{l}_{p}}{4}{\dot{T}}_{13}\right)}^{2}\right]}_{s=L}$$

(A.9)

Moreover, the plate kinetic energy arising from its rigid body rotation can be written in the following form

$${T}_{{K}_{P}}^{rot}=\frac{1}{2}{I}_{\zeta \zeta }{\omega }_{1}^{2}\left(L;t\right)+\frac{1}{2}{I}_{\eta \eta }{\omega }_{2}^{2}\left(L;t\right)+\frac{1}{2}{I}_{\xi \xi }{\omega }_{3}^{2}\left(L;t\right)$$

(A.10)

Hence, the total kinetic energy of the suspension microbeam and half of the paddle is given by the summation of Eqs. (A.7), (A.9) and (A.10):

$${T}_{K}^{tot}={T}_{K}+{T}_{{K}_{P}}^{tr}+{T}_{{K}_{P}}^{rot}$$

(A.11)

B.2 Absolute slopes

Figure 

Fig. 19

(a) Deformed configuration of a fiber with length of $ds$ aligned with the beam's elastic axis positioned at a distance $s$ from the origin $O$ of the inertial coordinate system $OXYZ$. (b) and (c) indicate the absolute slopes of the tangents to the projections of $d{s}^{\prime}$ onto the $\zeta \xi$- and $\zeta \eta$-plane, respectively, ${\theta }_{2}=\partial {u}_{3}^{0}/\partial s$ and ${\theta }_{3}=\partial {u}_{2}^{0}/\partial s$

19 illustrates the deformed status of a differential fiber $ds$ belonging to the beam's middle axis extruded from a material particle, which is initially located at a distance $s$ from the origin $O$ in the undeformed configuration. The length of this fiber is determined to be $d{s}^{\prime}=\left(1+e\right)ds$ after deformation, where $e$ is the longitudinal strain at that material particle, and is given as follows

$$e\left(s;t\right)=\sqrt{{\left(1+{u}^{\prime}\right)}^{2}+{{w}^{\prime}}^{2}}-1$$

(A.12)

The curvatures of the beam element in its deformed configuration are defined as follows [73]

$${\rho }_{1}\left(s;t\right)={\mathbf{i}}_{2}^{\prime} . {\mathbf{i}}_{3}={\phi }^{\prime}$$

(A.13a)

$${\rho }_{2}\left(s;t\right)={\mathbf{i}}_{3}^{\prime} . {\mathbf{i}}_{1}={\theta }^{\prime}\left(s;t\right)\text{cos}\phi $$

(A.13b)

$${\rho }_{3}\left(s;t\right)={\mathbf{i}}_{1}^{\prime} . {\mathbf{i}}_{2}=-{\theta }^{\prime}\left(s;t\right)\text{sin}\phi \approx 0$$

(A.13c)

Figure 19a depicts the variations in the directions of ${\mathbf{i}}_{3}$ and ${\mathbf{i}}_{2}$ as moving from point ${\text{P}}^{{{\prime}}}$ to ${\text{Q}}_{1}^{{{\prime}}}$ and ${\text{Q}}_{2}^{{{\prime}}}$ along the projections of $d{s}^{\prime}$ onto the $\zeta \xi$- and $\zeta \eta$-plane, introducing ${\rho }_{2}$ and${\rho }_{3}$, respectively. Based on Eq. (A.13c), $d{s}^{\prime}$ has indeed out-of-plane projection forming${\rho }_{3}$, which is negligible for small values of$\phi$. The slopes of the tangents to $d{s}^{\prime}$ at ${\text{P}}^{{{\prime}}}$ are determined to be zero with respect the $\zeta \eta \xi$ coordinate system. Integrating Eqs. (A.13a) and (A.13b) over $ds$ (for simplicity, not ${ds}^{\prime}$) by setting ${\rho }_{1}=\partial {\theta }_{1}(s;t)/\partial s$ and ${\rho }_{2}=\partial {\theta }_{2}(s;t)/\partial s$, however, yields non-zero values for the rotation of the face of the beam element, returning to the absolute slopes of the tangents to the curve $d{s}^{\prime}$ at${\text{P}}^{{{\prime}}}$.

To interpret these slopes, we rigidly transfer $\overline{{\text{P}}^{{{\prime}}}{\text{Q}}_{1}^{{{\prime}}}}$ and $\overline{{\text{P}}^{{{\prime}}}{\text{Q}}_{2}^{{{\prime}}}}$ onto the $xz$- and $xy$-plane, respectively, and define the local displacement field based on the Euler–Bernoulli beam theory, as follows

$$ \begin{gathered} U_{x} \left( {s,y,z;t} \right) = u_{1}^{0} \left( {s;t} \right) + z\sin \theta_{2} \left( {s;t} \right) - y\sin \theta_{3} \left( {s;t} \right) , \hfill \\ U_{y} \left( {s,y,z;t} \right) = u_{2}^{0} \left( {s;t} \right) - z \theta_{1} \left( {s;t} \right) , \hfill \\ U_{z} \left( {s,y,z;t} \right) = u_{3}^{0} \left( {s;t} \right) - z \left( {1 - \cos \theta_{2} \left( {s;t} \right)} \right) + y \theta_{1} \left( {s;t} \right) \hfill \\ \end{gathered} $$

(A.14)

This allows us to set certain values for the derivatives of ${u}_{2}^{0}$ and ${u}_{3}^{0}$ with respect to $ds$, meaning, ${\theta }_{3}$ and ${\theta }_{2}$, interpreting them as the absolute slopes of the tangents to $d{s}^{\prime}$, Fig. 19b and c. We have

$$ \begin{gathered} U_{i} \left( {s,y,z;t} \right) = 0 , u_{i}^{0} \left( {s;t} \right) = 0 , i = x, y, z \hfill \\ \theta_{1} \left( {s;t} \right) = \phi \left( {s;t} \right), \theta_{2} \left( {s;t} \right) \approx - w^{\prime}, \theta_{3} \left( {s;t} \right) = 0, \hfill \\ \frac{{\partial u_{1}^{0} }}{\partial s} = e\left( {s;t} \right), \frac{{\partial u_{2}^{0} }}{\partial s} = \theta_{3} \left( {s;t} \right), \frac{{\partial u_{3}^{0} }}{\partial s} = \theta_{2} \left( {s;t} \right) \hfill \\ \frac{{\partial \theta_{1} \left( {s;t} \right)}}{\partial s} = \rho_{1} \left( {s;t} \right), \frac{{\partial \theta_{2} \left( {s;t} \right)}}{\partial s} = \rho_{2} \left( {s;t} \right), \frac{{\partial \theta_{3} \left( {s;t} \right)}}{\partial s} = \rho_{3} \left( {s;t} \right). \hfill \\ \end{gathered} $$

(A.15)

The incorporation of the absolute slopes of the tangents to $d{s}^{\prime}$, ${\theta }_{2}$ and ${\theta }_{3}$, into the cross-sectional shear strain, ${\varepsilon }_{xy}$, never explored before, generates coupling between the transverse and torsional motions of the beam. It is important to highlight that $\partial {u}_{2}^{0}(s;t)/\partial s$ and $\partial {u}_{3}^{0}(s;t)/\partial s$ were assumed to be zero in [73].

B.3 Strain energy

We calculate the strain potential energy stored in the deformed structure using linear strain-displacement relationships for ${\varepsilon }_{xx}$ and ${\varepsilon }_{xz}$, and nonlinear strain–displacement relationship for ${\varepsilon }_{xy}$. Here, we consider the first order approximation of the in-plane bending curvature, ${\rho }_{2}(s;t)\approx -w^{{\prime}{\prime}}$, to incorporate the quadratic slopes into the shear strain component, ${\varepsilon }_{xy}$, and consequently the strain potential energy. According to the Green–Lagrange strain tensor defined in Cartesian coordinate system, we have.

$${\varepsilon }_{xx}= \frac{\partial {U}_{x}\left(s, y, z;t\right)}{\partial s} = e(s;t)-y{\rho }_{3}(s;t)+z{\rho }_{2}(s;t)$$

$${\varepsilon }_{xz}=\frac{1}{2}\left(\frac{\partial {U}_{x}\left(s, y, z;t\right)}{\partial z}+\frac{\partial {U}_{z}\left(s, y, z;t\right)}{\partial s}\right) =\frac{1}{2}y{\rho }_{1}(s;t)$$

$$ \begin{aligned} \varepsilon_{xy} = & \frac{1}{2}\left( {\frac{{\partial U_{x} }}{\partial y} + \frac{{\partial U_{y} }}{\partial s} + \frac{{\partial U_{x} }}{\partial s}\frac{{\partial U_{x} }}{\partial y} + \frac{{\partial U_{y} }}{\partial s}\frac{{\partial U_{y} }}{\partial y} + \frac{{\partial U_{z} }}{\partial s}\frac{{\partial U_{z} }}{\partial y}} \right) \\ & = - \frac{1}{2}z\rho_{1} + \frac{1}{2}\left[ {\left( {\frac{{\partial u_{1}^{0} }}{\partial s} + z\frac{{\partial \theta_{2} }}{\partial s} cos\theta_{2} - y\frac{{\partial \theta_{3} }}{\partial s} cos\theta_{3} } \right)\left( { - \sin \theta_{3} } \right) + \left( {\frac{{\partial u_{3}^{0} }}{\partial s} - z\frac{{\partial \theta_{2} }}{\partial s} sin\theta_{2} + y\frac{{\partial \theta_{1} }}{\partial s}} \right) \theta_{1} } \right] \\ & = - \frac{1}{2}z\rho_{1} + \frac{1}{2}\left( { - w^{\prime} - zw^{\prime\prime}w^{\prime} + y\phi^{\prime}} \right) \phi = - \frac{1}{2}z\phi^{\prime} + \frac{1}{2}\left( { - w^{\prime} - zw^{\prime\prime}w^{\prime} + y\phi^{\prime}} \right) \phi + H.O.T \\ \end{aligned} $$

(A.16)

The variations of the total strain potential energy of the structure take the form

$$\delta {U}_{s}^{tot} ={\smallint }_{\Omega }\left({\sigma }_{xx} \delta {\varepsilon }_{xx}+ 2{\sigma }_{xy} \delta {\varepsilon }_{xy}+2{\sigma }_{xz} \delta {\varepsilon }_{xz}\right)dV$$

(A.17)

B.4 Asymmetry-induced quadratic stiffness

Here, we demonstrate the origination of the quadratic stiffness that couples the in-plane bending and torsional motions in the torsional oscillator, Eq. (A.29). Using Eq. (A.16), the strain energy stored in volume $\Omega$ incorporated by the shear stress, ${\sigma }_{xy}$, and strain, ${\varepsilon }_{xy}$, is presented as follows.

$$ \begin{gathered} \delta U_{s} = \mathop \smallint \limits_{\Omega } 2\sigma _{{xy}} ~\delta \varepsilon _{{xy}} ~ \hfill \\ dV = \mathop \smallint \limits_{\Omega } \frac{1}{2}G\left( { - z\phi ^{\prime} - w^{\prime}\phi - zw^{\prime\prime}w^{\prime}\phi + y\phi ^{\prime}\phi ~} \right)\left( { - z\delta \phi ^{\prime} - \phi \delta w^{\prime} - w^{\prime}\delta \phi - zw^{\prime}\phi \delta w^{\prime\prime} - zw^{\prime\prime}\phi \delta w^{\prime} - z~w^{\prime\prime}w^{\prime}\delta \phi + y\phi \delta \phi ^{\prime} + y\phi ^{\prime}\delta \phi } \right) \hfill \\ ~dV = \mathop \smallint \limits_{\Omega } \left( {\frac{1}{2}Gzw^{\prime}\phi \delta \phi ^{\prime} + \ldots } \right)dV \hfill \\ \end{gathered} $$

(A.18)

It is crucial to note that the identification of the aforementioned term via inspecting the nonlinear shear strain component, ${\varepsilon }_{xy}$, relies on the analysis of the absolute slope $\frac{\partial {u}_{3}^{0}}{\partial s}={\theta }_{2}(s;t)$, a previously unexplored approach, rather than the nonlinear curvatures, $\frac{\partial {\theta }_{i}}{\partial s}={\rho }_{i}\left(s;t\right)$ $(i=\text{1,2},3)$.

Within the terms outlined in Eq. (A.18), the term depicted on the right-hand side of the equation gives rise to a quadratic stiffness term featured in the torsional equation of motion. This term couples the in-plane bending and torsional motions and is contingent on a non-zero first moment of area for the microbeam's cross-section. We utilize integration by parts to extract this quadratic coupling term, triggering the 2:1 autoparametric modal interaction between the flexural and torsional motions, and we get.

$$ \begin{aligned} \frac{1}{2}G\mathop \smallint \limits_{{\Omega }} \left( {zw^{\prime}\phi \delta \phi^{\prime}} \right)dAds = & \frac{1}{2}G\mathop {\mathop {\left( {\mathop \smallint \limits_{{A_{actual} }} zdA} \right)}\limits }\limits_{{Q_{yy} }} \left( {\mathop \smallint \limits_{0}^{L} w^{\prime}\phi \delta \phi^{\prime}ds} \right) \\ & = \frac{1}{2}GQ_{yy} \left( {\left. {\left( {w^{\prime}\phi } \right)\delta \phi } \right|_{s = 0}^{s = L} - \mathop \smallint \limits_{0}^{L} \left( {w^{\prime\prime}\phi + w^{\prime}\phi^{\prime}} \right)\delta \phi ds} \right) \\ & = \frac{1}{2}GQ_{yy} \left. {\left( {w^{\prime}\phi } \right)\delta \phi } \right|_{s = 0}^{s = L} - \mathop \smallint \limits_{0}^{L} \mathop {\mathop {\frac{1}{2}GQ_{yy} \left( {w^{\prime\prime}\phi + w^{\prime}\phi^{\prime}} \right)}\limits_{} }\limits_{{\text{Quadratic stiffness}}} \delta \phi ds \\ \end{aligned} $$

(A.19)

where $G$ stands for the shear modulus of the microbeam's material. There are two quadratic coupling terms in Eq. (A.19) arise from the shear strain, ${\varepsilon }_{xy}$. However, the term dependent on the curvature of the transverse motion, ${w}^{{\prime}{\prime}}\phi$, has a more significant impact on the initiation of the 2:1 modal interaction compared to the other term, ${w}^{\prime}{\phi }^{\prime}$. The existence of these terms is dependent on a non-vanishing first moment of area of the microbeam's cross-section. It is noteworthy that the identification of the above-stated quadratic stiffness is also doable using global displacement fields widely existing in the literature of bending and torsional motions for beams [98,99,100,101]. However, the derivation of equations of motion for beams simultaneously addressing nonlinear curvatures and slopes necessitates the employment of the concept of local displacement field.

B.5 Electrostatic force and torque

The total in-plane MEMS capacitance is the summation of the capacitance formed between the suspension microbeams and the stationary side electrodes, ${C}_{b}$, and the capacitance contributed by the middle plate and the middle side actuating electrode, ${C}_{p}$, Fig. 

Fig. 20

Schematic of the electrostatic MEMS actuator and its RLC circuit (the MEMS capacitance, ${C}_{m}$)

20. According to the parallel-plate capacitance assumption, the differential capacitance, $d{C}_{b}(s;t)$, formed between the differential side surface of the microbeams, $d{A}_{s}=d\zeta ds$, and the actuating electrode can be written as below

$$d{C}_{b}\left(s;t\right)=\frac{{\epsilon }_{0} d\zeta ds}{d(\zeta )}$$

(A.20)

where, $\varepsilon$ defines the permittivity of the capacitive medium, and $d(\zeta )$ denotes the in-plane distance between the differential side surface, $d{A}_{s}$, and the actuating electrode expressed in the following form

$$ \begin{gathered} d\left( {s,\zeta ;t} \right) = \left( {{\text{g}}_{{\text{o}}} + \frac{h}{2}} \right) - \left( {w\left( {s;t} \right) + \sqrt {\frac{{h^{2} }}{4} + \zeta^{2} } {\text{cos}}\left( {\psi + \phi \left( {s;t} \right)} \right)} \right) \hfill \\ r = \sqrt {\frac{{h^{2} }}{4} + \zeta^{2} } , \psi = \tan^{ - 1} \left( {\frac{2\zeta }{h}} \right) \hfill \\ \end{gathered} $$

(A.21)

The capacitance per unit length of the microbeam can be written as follows

$$ C_{b} \left( {s;t} \right) = \left\{ {\begin{array}{*{20}c} {\mathop \smallint \limits_{{ - \frac{b}{2}}}^{{\frac{1}{2}\left( {\frac{{b - h~\sin \phi }}{{\cos \phi }}} \right)}} \frac{{ \in _{0} }}{{d\left( {s,\zeta ;t} \right)}}d\zeta; \;0 \le \phi < 2\tan ^{{ - 1}} \left( {\frac{b}{h}} \right)} \\ {\mathop \int \limits_{{ - \frac{1}{2}\left( {\frac{{b + h~\sin \phi }}{{\cos \phi }}} \right)}}^{{\frac{b}{2}}} \frac{{ \in _{0} }}{{d\left( {s,\zeta ;t} \right)}}d\zeta; \; - 2\tan ^{{ - 1}} \left( {\frac{b}{h}} \right) < \phi \le 0} \\ \end{array} } \right. $$

(A.22)

Considering the electrical potential energy stored in per unit length of the beam-capacitance in the form of ${U}_{b}^{el}\left(s;t\right)=1/2{C}_{b}\left(s;t\right)V{\left(t\right)}^{2}$, we can obtain the induced electrostatic force and torque applied to per unit length of the microbeam as follows

$$ F_{z}^{{el}} (w,\phi ) = \frac{{\partial U_{b}^{{el}} }}{{\partial w}} = \left\{ {\begin{array}{*{20}c} {\smallint _{{ - \frac{b}{2}}}^{{\frac{1}{2}\left( {\frac{{b - h{\text{ sin}}\phi }}{{{\text{cos}}\phi }}} \right)}} \frac{{ \in _{0} V(t)^{2} }}{{2\left( { - \sqrt {\frac{{h^{2} }}{4} + \zeta ^{2} } {\text{cos}}\chi + \frac{h}{2} + {\text{g}}_{0} - w} \right)^{2} }}d\zeta ,0 \le \phi < 2tan^{{ - 1}} \left( {\frac{b}{h}} \right)} \\ {\smallint _{{ - \frac{1}{2}\left( {\frac{{b + h{\text{sin}}\phi }}{{{\text{cos}}\phi }}} \right)}}^{{\frac{b}{2}}} \frac{{ \in _{0} V(t)^{2} }}{{2\left( { - \sqrt {\frac{{h^{2} }}{4} + \zeta ^{2} } {\text{cos}}\chi + \frac{h}{2} + {\text{g}}_{0} - w} \right)^{2} }}d\zeta , - 2{\text{tan}}^{{ - 1}} \left( {\frac{b}{h}} \right) < \phi \le 0} \\ \end{array} } \right. $$

(A.23)

$${T}_{x}^{el}\left(w,\phi \right)=\frac{\partial {U}_{b}^{el}}{\partial \phi }=-\left\{\begin{array}{c}{\int }_{-\frac{b}{2}}^{\frac{1}{2}\left(\frac{b-h\text{ sin}\phi }{\text{cos}\phi }\right)}\frac{{\epsilon }_{0}{V(t)}^{2}\sqrt{\frac{{h}^{2}}{4}+{\zeta }^{2}}\text{sin}\chi }{2{\left(-\sqrt{\frac{{h}^{2}}{4}+{\zeta }^{2}}\text{cos}\chi +\frac{h}{2}+{\text{g}}_{0}-w\right)}^{2}}d\zeta , 0\le \phi <2{\text{tan}}^{-1}\left(\frac{b}{h}\right)\\ {\int }_{-\frac{1}{2}\left(\frac{b+h {sin}\phi }{{cos}\phi }\right)}^\frac{b}{2}\frac{{\epsilon }_{0}{V(t)}^{2}\sqrt{\frac{{h}^{2}}{4}+{\zeta }^{2}}\text{sin}\chi }{2{\left(-\sqrt{\frac{{h}^{2}}{4}+{\zeta }^{2}}\text{cos}\chi +\frac{h}{2}+{\text{g}}_{0}-w\right)}^{2}}d\zeta , -2{\text{tan}}^{-1}\left(\frac{b}{h}\right)<\phi \le 0\end{array}\right.$$

(A.24)

where, $\chi (s,\zeta ;t)={\text{tan}}^{-1}\left(\frac{2\zeta }{h}\right)+\phi (s;t)$. The induced electrostatic force and torque applied to the rigid plate can be obtained similarly and are denoted by ${F}_{pz}^{el}$ and ${T}_{px}^{el}$, respectively. The conservative work done by them are expressed in the following way.

$$\delta {W}_{ext} ={\int }_{0}^{L}\left({F}_{z}^{el} \delta w+{T}_{x}^{el} \delta \varphi \right) ds +{F}_{pz}^{el}\left(L;t\right) \delta w\left(L;t\right)+{T}_{px}^{el}\left(L;t\right) \delta \varphi (L;t)$$

(A.25)

The non-conservative work done by air viscous damping in the in-plane bending and torsional directions are expressed

$$\delta {W}_{ext}^{nc} ={\int }_{0}^{L}\left({c}_{w}\dot{w} \delta w+{c}_{\varphi }\dot{\varphi } \delta \varphi \right) ds+{c}_{w}\dot{w}\left(L;t\right)\delta w\left(L;t\right)+{c}_{\varphi }\dot{\varphi }\left(L;t\right) \delta \varphi \left(L;t\right)$$

(A.26)

B.6 Half-structured EoM

Finally, the equations of motion of the electrostatic MEMS actuator are obtained employing the extended Hamilton's principle, minimizing the system's Lagrangian between two arbitrary instants, ${t}_{1}$ and ${t}_{2}$. Using Eqs. (A.11), (A.17), (A.25), and (A.26), we have

$${\int }_{{t}_{1}}^{{t}_{2}}\left(\delta {T}_{K}^{tot}-\delta {U}_{s}^{tot}+\delta {w}_{ext}+\delta {w}_{ext}^{nc}\right) dt=0$$

(A.27)

Performing a straightforward mathematical manipulation using variational calculus and truncating the nonlinear stiffness and inertia (arising from nonlinear curvature) up to full third order, and incorporating the $u$-motion into the $w$ and $\phi$ motions by assuming the microbeam's longitudinal inertia is negligible within the forcing frequency range of interest, $\rho A {\partial }^{2}u/\partial {t}^{2}\approx 0,$ yields to the following dimensional equations of motion and their corresponding boundary conditions.

$$ \begin{aligned} \delta w&:\quad\frac{{\partial ^{2} w}}{{\partial t^{2} }} + c_{w} \frac{{\partial w}}{{\partial t}} \\ & \quad + \alpha _{2} \left( {\phi \left( {s,t} \right)^{2} \frac{{\partial ^{4} w}}{{\partial s^{2} {\mkern 1mu} \partial t^{2} }} + 2\frac{{\partial \phi }}{{\partial t}}\phi \left( {s,t} \right)\frac{{\partial ^{3} w}}{{\partial s^{2} {\mkern 1mu} \partial t}} + 2\frac{{\partial \phi }}{{\partial s}}\phi \left( {s,t} \right)\frac{{\partial ^{3} w}}{{\partial s{\mkern 1mu} \partial t^{2} }}} \right. \\ &\quad\left. { \quad + 2\phi \left( {s,t} \right)\frac{{\partial ^{2} w}}{{\partial s{\mkern 1mu} \partial t}}\frac{{\partial ^{2} \phi }}{{\partial s{\mkern 1mu} \partial t}} - \frac{{\partial ^{4} w}}{{\partial s^{2} {\mkern 1mu} \partial t^{2} }} + 2\frac{{\partial \phi }}{{\partial s}}\frac{{\partial \phi }}{{\partial t}}\frac{{\partial ^{2} w}}{{\partial s{\mkern 1mu} \partial t}}} \right) \\ & \quad + \alpha _{5} \left( { - \phi \left( {s,t} \right)^{2} \frac{{\partial ^{4} w}}{{\partial s^{2} {\mkern 1mu} \partial t^{2} }} - 2\frac{{\partial \phi }}{{\partial t}}\phi \left( {s,t} \right)\frac{{\partial ^{3} w}}{{\partial s^{2} {\mkern 1mu} \partial t}} - 2\frac{{\partial \phi }}{{\partial s}}\phi \left( {s,t} \right)\frac{{\partial ^{3} w}}{{\partial s{\mkern 1mu} \partial t^{2} }}} \right. \\ &\quad\left. { - 2\phi \left( {s,t} \right)\frac{{\partial ^{2} w}}{{\partial s{\mkern 1mu} \partial t}}\frac{{\partial ^{2} \phi }}{{\partial s{\mkern 1mu} \partial t}} - 2\frac{{\partial \phi }}{{\partial s}}\frac{{\partial \phi }}{{\partial t}}\frac{{\partial ^{2} w}}{{\partial s{\mkern 1mu} \partial t}}} \right) \\ & \quad + \alpha _{1} \left( {\frac{{\partial w}}{{\partial s}}\left( {\frac{{\partial w}}{{\partial s}}\frac{{\partial ^{4} w}}{{\partial s^{4} }} + 2\frac{{\partial ^{2} w}}{{\partial s^{2} }}\frac{{\partial ^{3} w}}{{\partial s^{3} }}} \right) - \frac{1}{L}\frac{{\partial ^{2} w}}{{\partial s^{2} }}\int\limits_{0}^{L} {\frac{{\partial w}}{{\partial s}}} \frac{{\partial ^{3} w}}{{\partial s^{3} }}{\text{d}}s} \right) - \alpha _{4} \frac{{\partial ^{2} w}}{{\partial s^{2} }}\int\limits_{0}^{L} {\left( {\frac{{\partial w}}{{\partial s}}} \right)^{2} } {\text{d}}s \\ & \quad + \alpha _{1} \left( { - \frac{{\partial ^{4} w}}{{\partial s^{4} }}\phi \left( {s,t} \right)^{2} - 4\frac{{\partial ^{3} w}}{{\partial s^{3} }}\frac{{\partial \phi }}{{\partial s}}\phi \left( {s,t} \right) - 2\frac{{\partial ^{2} w}}{{\partial s^{2} }}\left( {\frac{{\partial ^{2} \phi }}{{\partial s^{2} }}\phi \left( {s,t} \right) - \frac{{\partial w}}{{\partial s}}\frac{{\partial ^{3} w}}{{\partial s^{3} }}} \right)} \right. \\ & \quad \left. { - \frac{1}{L}\frac{{\partial ^{4} w}}{{\partial s^{4} }}\int\limits_{0}^{L} {\left( {\frac{{\partial w}}{{\partial s}}} \right)^{2} } {\text{d}}s + \frac{{\partial ^{4} w}}{{\partial s^{4} }} - 2\frac{{\partial ^{2} w}}{{\partial s^{2} }}\left( {\frac{{\partial \phi }}{{\partial s}}} \right)^{2} + \left( {\frac{{\partial ^{2} w}}{{\partial s^{2} }}} \right)^{3} } \right) \\ & \quad + \alpha _{6} \left( {\frac{{\partial ^{4} w}}{{\partial s^{4} }}\phi \left( {s,t} \right)^{2} + 4\frac{{\partial ^{3} w}}{{\partial s^{3} }}\frac{{\partial \phi }}{{\partial s}}\phi \left( {s,t} \right) + 2\frac{{\partial ^{2} w}}{{\partial s^{2} }}\frac{{\partial ^{2} \phi }}{{\partial s^{2} }}\phi \left( {s,t} \right) + 2\frac{{\partial ^{2} w}}{{\partial s^{2} }}\left( {\frac{{\partial \phi }}{{\partial s}}} \right)^{2} } \right) \\ & = \alpha _{e} \left\{ {\begin{array}{*{20}c} {\int\limits_{{ - \frac{b}{2}}}^{{\frac{1}{2}\left( {\frac{{b - h~\sin \phi }}{{\cos \phi }}} \right)}} {\frac{{V\left( t \right)^{2} }}{{\left( { - \sqrt {\frac{{h^{2} }}{4} + \zeta ^{2} } \cos \left( {{\text{tan}}^{{ - 1}} \left( {\frac{{2\zeta }}{h}} \right) + \phi } \right) + \frac{h}{2} + {\text{g}}_{0} - w} \right)^{2} }}} d\zeta ;~~0 \le \phi < 2\tan ^{{ - 1}} \left( {\frac{b}{h}} \right)} \\ {\int\limits_{{ - \frac{1}{2}\left( {\frac{{b + h~\sin \phi }}{{\cos \phi }}} \right)}}^{{\frac{b}{2}}} {\frac{{V\left( t \right)^{2} }}{{\left( { - \sqrt {\frac{{h^{2} }}{4} + \zeta ^{2} } \cos \left( {{\text{tan}}^{{ - 1}} \left( {\frac{{2\zeta }}{h}} \right) + \phi } \right) + \frac{h}{2} + {\text{g}}_{0} - w} \right)^{2} }}} d\zeta ;~~ - 2\tan ^{{ - 1}} \left( {\frac{b}{h}} \right) < \phi \le 0} \\ \end{array} } \right. \\ \end{aligned} $$

(A.28)

$$ \begin{gathered} \delta \phi :\frac{{\partial ^{2} \phi }}{{\partial t^{2} }} + c_{\phi } \frac{{\partial \phi }}{{\partial t}} - \beta _{1} \frac{{\partial ^{2} \phi }}{{\partial s^{2} }} + \beta _{5} \phi \left( {s,t} \right)\left( {\frac{{\partial ^{2} w}}{{\partial s\,\partial t}}} \right)^{2} - \beta _{6} \phi \left( {s,t} \right)\left( {\frac{{\partial ^{2} w}}{{\partial s\,\partial t}}} \right)^{2} \hfill \\ - \beta _{3} \left( {\frac{{\partial ^{2} w}}{{\partial s^{2} }}} \right)^{2} \phi \left( {s,t} \right) + \beta _{4} \left( {\frac{{\partial ^{2} w}}{{\partial s^{2} }}} \right)^{2} \phi \left( {s,t} \right) - \beta _{q} \frac{{\partial ^{2} w}}{{\partial s^{2} }}\phi = \hfill \\ \beta _{e} = \left\{ {\begin{array}{*{20}c} { - \mathop \smallint \limits_{{ - \frac{b}{2}}}^{{\frac{1}{2}\left( {\frac{{b - h~\sin \phi }}{{\cos \phi }}} \right)}} \frac{{\sqrt {\frac{{h^{2} }}{4} + \zeta ^{2} } \sin \left( {{\text{tan}}^{{ - 1}} \left( {\frac{{2\zeta }}{h}} \right) + \phi } \right)V\left( t \right)^{2} }}{{\left( { - \sqrt {\frac{{h^{2} }}{4} + \zeta ^{2} } \cos \left( {{\text{tan}}^{{ - 1}} \left( {\frac{{2\zeta }}{h}} \right) + \phi } \right) + \frac{h}{2} + {\text{g}}_{0} - w} \right)^{2} }}d\zeta ~;} \; {~0 \le \phi < 2\tan ^{{ - 1}} \left( {\frac{b}{h}} \right)} \\ { - \mathop \smallint \limits_{{ - \frac{1}{2}\left( {\frac{{b + h~\sin \phi }}{{\cos \phi }}} \right)}}^{{\frac{b}{2}}} \frac{{\sqrt {\frac{{h^{2} }}{4} + \zeta ^{2} } \sin \left( {{\text{tan}}^{{ - 1}} \left( {\frac{{2\zeta }}{h}} \right) + \phi } \right)V\left( t \right)^{2} }}{{\left( { - \sqrt {\frac{{h^{2} }}{4} + \zeta ^{2} } \cos \left( {{\text{tan}}^{{ - 1}} \left( {\frac{{2\zeta }}{h}} \right) + \phi } \right) + \frac{h}{2} + {\text{g}}_{0} - w} \right)^{2} }}d\zeta ~;} \; { - 2\tan ^{{ - 1}} \left( {\frac{b}{h}} \right) < \phi \le 0} \\ \end{array} } \right. \hfill \\ \end{gathered} $$

(A.29)

Subject to the following geometrically linear essential and natural boundary conditions.

$$w={w}^{{^{\prime}}}=0 ; \phi =0 at x=0$$

$${w}^{\prime}=0 at x=L$$

$$ \begin{gathered} - \frac{{\partial^{2} w\left( {L;t} \right)}}{{\partial t^{2} }} + \alpha_{3} \frac{{\partial^{3} w\left( {L;t} \right)}}{{\partial s^{3} }} \hfill \\ + \alpha_{e}^{b} \left\{ {\begin{array}{*{20}c} {\mathop \int \limits_{{ - \frac{{b_{p} }}{2}}}^{{\frac{1}{2}\left( {\frac{{b_{p} - h_{p} \sin \phi }}{\cos \phi }} \right)}} \frac{{V\left( t \right)^{2} }}{{\left( { - \sqrt {\frac{{h_{p}^{2} }}{4} + \zeta^{2} } \cos \left( {{\text{tan}}^{ - 1} \left( {\frac{2\zeta }{{h_{p} }}} \right) + \phi } \right) + \frac{{h_{p} }}{2} + {\text{g}}_{0} - w} \right)^{2} }}d\zeta ; 0 \le \phi < 2\tan^{ - 1} \left( {\frac{{b_{p} }}{{h_{p} }}} \right)} \\ {\mathop \int \limits_{{ - \frac{1}{2}\left( {\frac{{b_{p} + h_{p} \sin \phi }}{\cos \phi }} \right)}}^{{\frac{{b_{p} }}{2}}} \frac{{V\left( t \right)^{2} }}{{\left( { - \sqrt {\frac{{h_{p}^{2} }}{4} + \zeta^{2} } \cos \left( {{\text{tan}}^{ - 1} \left( {\frac{2\zeta }{{h_{p} }}} \right) + \phi } \right) + \frac{{h_{p} }}{2} + {\text{g}}_{0} - w} \right)^{2} }}d\zeta ; - 2\tan^{ - 1} \left( {\frac{{b_{p} }}{{h_{p} }}} \right) < \phi \le 0} \\ \end{array} } \right. \hfill \\ = 0 ; at x = L \hfill \\ \frac{{{\text{d}}^{2} \phi \left( {L;t} \right)}}{{{\text{d}}t^{2} }} + \beta_{2} \frac{{\partial \phi \left( {L;t} \right)}}{\partial s} \hfill \\ + \beta_{e}^{b} \left\{ {\begin{array}{*{20}c} {\mathop \int \limits_{{ - \frac{{b_{p} }}{2}}}^{{\frac{1}{2}\left( {\frac{{b_{p} - h_{p} \sin \phi }}{\cos \phi }} \right)}} \frac{{\sqrt {\frac{{h_{p}^{2} }}{4} + \zeta^{2} } \sin \left( {{\text{tan}}^{ - 1} \left( {\frac{2\zeta }{{h_{p} }}} \right) + \phi } \right)V\left( t \right)^{2} }}{{\left( { - \sqrt {\frac{{h_{p}^{2} }}{4} + \zeta^{2} } \cos \left( {{\text{tan}}^{ - 1} \left( {\frac{2\zeta }{{h_{p} }}} \right) + \phi } \right) + \frac{{h_{p} }}{2} + {\text{g}}_{0} - w} \right)^{2} }}d\zeta ; 0 \le \phi < 2\tan^{ - 1} \left( {\frac{{b_{p} }}{{h_{p} }}} \right)} \\ {\mathop \int \limits_{{ - \frac{1}{2}\left( {\frac{{b_{p} + h_{p} \sin \phi }}{\cos \phi }} \right)}}^{{b_{p} }} \frac{{\sqrt {\frac{{h_{p}^{2} }}{4} + \zeta^{2} } \sin \left( {{\text{tan}}^{ - 1} \left( {\frac{2\zeta }{{h_{p} }}} \right) + \phi } \right)V\left( t \right)^{2} }}{{\left( { - \sqrt {\frac{{h_{p}^{2} }}{4} + \zeta^{2} } \cos \left( {{\text{tan}}^{ - 1} \left( {\frac{2\zeta }{{h_{p} }}} \right) + \phi } \right) + \frac{{h_{p} }}{2} + {\text{g}}_{0} - w} \right)^{2} }}d\zeta ; - 2\tan^{ - 1} \left( {\frac{{b_{p} }}{{h_{p} }}} \right) < \phi \le 0} \\ \end{array} } \right. \hfill \\ = 0 ;at x = L \hfill \\ \end{gathered} $$

(A.30)

where the dimensional parameters are defined as follows

$$ \begin{gathered} \alpha_{1} = \frac{{EI_{yy} }}{\rho A}, \alpha_{2} = \frac{{I_{yy} }}{A}, \alpha_{3} = \frac{{EI_{yy} }}{{M_{p} }}, \alpha_{4} = \frac{E}{2\rho L}, \alpha_{5} = \frac{{I_{zz} }}{A}, \alpha_{6} = \frac{{EI_{zz} }}{\rho A}, \hfill \\ \alpha_{e} = \frac{{ \in_{0} }}{2\rho A}, \alpha_{e}^{b} = \frac{{ \in_{0} l_{p} }}{{4M_{p} }}, \hfill \\ \beta_{1} = \frac{G}{2\rho }, \beta_{2} = \frac{{GJ_{o} }}{{2J_{o}^{p} }}, \beta_{3} = \frac{{EI_{yy} }}{{\rho J_{o} }} , \beta_{4} = \frac{{EI_{zz} }}{{\rho J_{o} }} , \beta_{5} = \frac{{I_{yy} }}{{J_{o} }} , \beta_{6} = \frac{{I_{zz} }}{{J_{o} }} , \beta_{e} = \frac{{ \in_{0} }}{{2\rho J_{o} }}, \beta_{e}^{b} = \frac{{ \in_{0} l_{p} }}{{4J_{o}^{p} }}, \beta_{q} = \frac{{GQ_{yy} }}{{2\rho J_{o} }}. \hfill \\ \end{gathered} $$

(A.31)

Appendix C

The coefficients of the stiffness terms and the electrostatic force and torque appearing in Eqs. (10) and (11) are defined as

$$ \begin{gathered} K_{ni}^{l\left( 1 \right)} = \mathop \int \limits_{0}^{L} {\Psi }_{{\text{n}}} {\Psi }_{{\text{i}}} ds , K_{ni}^{l\left( 2 \right)} = \mathop \int \limits_{0}^{L} {\Psi }_{{\text{n}}}^{\prime} {\Psi }_{{\text{i}}}^{{\prime\prime\prime}} ds , K_{nijk}^{1} = \mathop \int \limits_{0}^{L} {\Psi }_{{\text{n}}} {\Phi }_{{\text{i}}} {\Phi }_{{\text{j}}} {\Psi }_{{\text{k}}}^{{{\prime\prime}}} ds , \hfill \\ K_{nijk}^{2} = \mathop \int \limits_{0}^{L} {\Psi }_{{\text{n}}} {\Phi }_{{\text{i}}} {\Phi }_{{\text{j}}}^{\prime} {\Psi }_{{\text{k}}}^{\prime} ds \hfill \\ K_{nijk}^{3} = \mathop \int \limits_{0}^{L} {\Psi }_{{\text{n}}} {\Phi }_{{\text{i}}}^{\prime} {\Phi }_{{\text{j}}} {\Psi }_{{\text{k}}}^{\prime} ds, K_{nijk}^{\delta \left( 1 \right)} = \mathop \int \limits_{0}^{L} {\Psi }_{{\text{n}}} {\Psi }_{{\text{i}}}^{\prime} {\Psi }_{{\text{j}}}^{\prime} {\Psi }_{{\text{k}}}^{{{\prime\prime\prime\prime}}} ds , K_{nijk}^{\delta \left( 2 \right)} = \mathop \int \limits_{0}^{L} {\Psi }_{{\text{n}}} {\Psi }_{{\text{i}}}^{\prime} {\Psi }_{{\text{j}}}^{{{\prime\prime}}} {\Psi }_{{\text{k}}}^{{{\prime\prime\prime}}} ds, K_{nijk}^{\delta \left( 3 \right)} = \mathop \int \limits_{0}^{L} {\Psi }_{{\text{n}}} {\Psi }_{{\text{i}}}^{{{\prime\prime}}} {\Psi }_{{\text{j}}}^{{{\prime\prime}}} {\Psi }_{{\text{k}}}^{{{\prime\prime}}} ds \hfill \\ K_{nijk}^{\delta \left( 4 \right)} = \left( {\mathop \int \limits_{0}^{L} {\Psi }_{{\text{n}}} {\Psi }_{{\text{i}}}^{{{\prime\prime\prime\prime}}} ds} \right)\left( {\mathop \int \limits_{0}^{L} {\Psi }_{{\text{j}}}^{\prime} {\Psi }_{{\text{k}}}^{\prime} ds} \right) + \left( {\mathop \int \limits_{0}^{L} {\Psi }_{{\text{n}}} {\Psi }_{{\text{i}}}^{{{\prime\prime}}} ds} \right)\left( {\mathop \int \limits_{0}^{L} {\Psi }_{{\text{j}}}^{\prime} {\Psi }_{{\text{k}}}^{{{\prime\prime\prime}}} ds} \right) \hfill \\ K_{nijk}^{ms} = \left( {\mathop \int \limits_{0}^{L} {\Psi }_{{\text{n}}} {\Psi }_{{\text{i}}}^{{{\prime\prime}}} ds} \right)\left( {\mathop \int \limits_{0}^{L} {\Psi }_{{\text{j}}}^{\prime} {\Psi }_{{\text{k}}}^{\prime} ds} \right) \hfill \\ K_{nijk}^{c\left( 1 \right)} = \mathop \int \limits_{0}^{L} {\Psi }_{{\text{n}}} {\Phi }_{{\text{i}}} {\Phi }_{{\text{j}}} {\Psi }_{{\text{k}}}^{{{\prime\prime\prime\prime}}} ds , K_{nijk}^{c\left( 2 \right)} = \mathop \int \limits_{0}^{L} {\Psi }_{{\text{n}}} {\Phi }_{{\text{i}}} {\Phi }_{{\text{j}}}^{\prime} {\Psi }_{{\text{k}}}^{{{\prime\prime\prime}}} ds, K_{nijk}^{c\left( 3 \right)} = \mathop \int \limits_{0}^{L} {\Psi }_{{\text{n}}} {\Phi }_{{\text{i}}} {\Phi }_{{\text{j}}}^{{\prime\prime}} {\Psi }_{{\text{k}}}^{{{\prime\prime}}} ds , K_{nijk}^{c\left( 4 \right)} = \mathop \int \limits_{0}^{L} {\Psi }_{{\text{n}}} {\Phi }_{{\text{i}}}{\prime} {\Phi }_{{\text{j}}}{\prime} {\Psi }_{{\text{k}}}^{{{\prime\prime}}} ds \hfill \\ Kt_{ni}^{l\left( 1 \right)} = \mathop \int \limits_{0}^{L} {\Phi }_{{\text{n}}} {\Phi }_{{\text{i}}} ds , Kt_{ni}^{l\left( 2 \right)} = \mathop \int \limits_{0}^{L} {\Phi }_{{\text{n}}}^{\prime} {\Phi }_{{\text{i}}}^{\prime} ds \hfill \\ Kt_{nijk}^{c\left( 1 \right)} = \mathop \int \limits_{0}^{L} {\Phi }_{{\text{n}}} {\Phi }_{{\text{i}}} {\Psi }_{{\text{j}}}^{\prime} {\Psi }_{{\text{k}}}^{\prime} ds , Kt_{nijk}^{c\left( 2 \right)} = \mathop \int \limits_{0}^{L} {\Phi }_{{\text{n}}} {\Phi }_{{\text{i}}} {\Psi }_{{\text{j}}}^{{{\prime\prime}}} {\Psi }_{{\text{k}}}^{{{\prime\prime}}} ds , \hfill \\ Kt_{nij}^{q} = \mathop \int \limits_{0}^{L} {\Phi }_{{\text{n}}} {\Phi }_{{\text{i}}} {\Psi }_{{\text{j}}}^{{{\prime\prime}}} ds \hfill \\ \end{gathered} $$

$$ \begin{aligned} F_{n} \left( t \right) = & \alpha _{e} \left( {\frac{Q}{{C_{{tot}} }}} \right)^{2} ~\left\{ {\begin{array}{*{20}c} {\mathop \int \limits_{0}^{L} \Psi_{{\text{n}}} \left( s \right)\mathop \int \limits_{{ - \frac{b}{2}}}^{{\frac{1}{2}\left( {\frac{{b - h~\sin \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} } \right)}}{{\cos \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} } \right)}}} \right)}} F_{{n1}} \left( {p_{i} ,q_{i} ;h,s,\zeta } \right)d\zeta ds~;~~} \; {0 \le \phi < 2\tan ^{{ - 1}} \left( {\frac{b}{h}} \right)} \\ {\mathop \int \limits_{0}^{L} \Psi_{{\text{n}}} \left( s \right)\mathop \int \limits_{{ - \frac{1}{2}\left( {\frac{{b + h~\sin \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} } \right)}}{{\cos \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} } \right)}}} \right)}}^{{\frac{b}{2}}} F_{{n1}} \left( {p_{i} ,q_{i} ;h,s,\zeta } \right)d\zeta ds;} \; { - 2\tan ^{{ - 1}} \left( {\frac{b}{h}} \right) < \phi \le 0~~} \\ \end{array} } \right. \\ & \quad + \alpha _{1} \frac{{\alpha _{e}^{b} }}{{\alpha _{3} }}\left( {\frac{Q}{{C_{{tot}} }}} \right)^{2} \Psi_{{\text{n}}} \left( L \right)\left\{ {\begin{array}{*{20}c} {\mathop \int \limits_{{ - \frac{{b_{p} }}{2}}}^{{\frac{1}{2}\left( {\frac{{b_{p} - h_{p} \sin \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} } \right)}}{{\cos \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi _{i} } \right)}}} \right)}} F_{{n1}} \left( {p_{i} ,q_{i} ;h_{p} ,L,\zeta } \right)d\zeta ;}\; {0 \le \phi < 2\tan ^{{ - 1}} \left( {\frac{{b_{p} }}{{h_{p} }}} \right)} \\ {\mathop \int \limits_{{ - \frac{1}{2}\left( {\frac{{b_{p} + h_{p} \sin \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} } \right)}}{{\cos \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} } \right)}}} \right)}}^{{\frac{{b_{p} }}{2}}} F_{{n1}} \left( {p_{i} ,q_{i} ;h_{p} ,L,\zeta } \right)d\zeta ;} \; {~ - 2\tan ^{{ - 1}} \left( {\frac{{b_{p} }}{{h_{p} }}} \right) < \phi \le 0~~} \\ \end{array} } \right. \\ F_{n} \left( t \right) = & \beta _{e} \left( {\frac{Q}{{C_{{tot}} }}} \right)^{2} ~\left\{ {\begin{array}{*{20}c} {\mathop \int \limits_{0}^{L} \Psi_{{\text{n}}} \left( s \right)\mathop \int \limits_{{ - \frac{b}{2}}}^{{\frac{1}{2}\left( {\frac{{b - h~\sin \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} } \right)}}{{\cos \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} } \right)}}} \right)}} F_{{n1}} \left( {p_{i} ,q_{i} ;h,s,\zeta } \right)d\zeta ds~;} \; {0 \le \phi < 2\tan ^{{ - 1}} \left( {\frac{b}{h}} \right)} \\ {\mathop \int \limits_{0}^{L} \Psi_{{\text{n}}} \left( s \right)\mathop \int \limits_{{ - \frac{1}{2}\left( {\frac{{b + h~\sin \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} } \right)}}{{\cos \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} } \right)}}} \right)}}^{{\frac{b}{2}}} F_{{n1}} \left( {p_{i} ,q_{i} ;h,s,\zeta } \right)d\zeta ds;} \; { - 2\tan ^{{ - 1}} \left( {\frac{b}{h}} \right) < \phi \le 0~~} \\ \end{array} } \right. \\ & \quad - \beta _{1} \frac{{\beta _{e}^{b} }}{{\beta _{2} }}\left( {\frac{Q}{{C_{{tot}} }}} \right)^{2} \Phi_{{\text{n}}} \left( L \right)\left\{ {\begin{array}{*{20}c} {\mathop \int \limits_{{ - \frac{{b_{p} }}{2}}}^{{\frac{1}{2}\left( {\frac{{b_{p} - h_{p} \sin \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} } \right)}}{{\cos \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi _{i} } \right)}}} \right)}} F_{{n1}}^{t} \left( {p_{i} ,q_{i} ;h_{p} ,L,\zeta } \right)d\zeta ~;} \; {~0 \le \phi < 2\tan ^{{ - 1}} \left( {\frac{{b_{p} }}{{h_{p} }}} \right)} \\ {\mathop \int \limits_{{ - \frac{1}{2}\left( {\frac{{b_{p} + h_{p} \sin \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} } \right)}}{{\cos \left( {\mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} } \right)}}} \right)}}^{{\frac{{b_{p} }}{2}}} F_{{n1}}^{t} \left( {p_{i} ,q_{i} ;h_{p} ,L,\zeta } \right)d\zeta ;} \; {~ - 2\tan ^{{ - 1}} \left( {\frac{{b_{p} }}{{h_{p} }}} \right) < \phi \le 0} \\ \end{array} } \right. \\ F_{{n1}} (p_{i} ,q_{i} ;H,\zeta ) &= \frac{1}{( - \sqrt {\left( {H^{2} /4 + \zeta ^{2} } \right)} cos(tan^{{( - 1)}} (2\zeta /H) + \sum {_{{(i = 1)}}^{N} } p_{i} \Phi _{i} (s)) + H/2 + g_{0} - \sum {_{{(i = 1)}}^{N} } q_{i} \Phi _{i} (s))^{2}} , \\ F_{{n1}}^{t} \left( {p_{i} ,q_{i} ;H,s,\zeta } \right) &= \frac{{\sqrt {\frac{{H^{2} }}{4} + \zeta ^{2} } \sin \left( {{\text{tan}}^{{ - 1}} \left( {\frac{{2\zeta }}{H}} \right) + \mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} \left( s \right)} \right)}}{{\left( { - \sqrt {\frac{{H^{2} }}{4} + \zeta ^{2} } \cos \left( {{\text{tan}}^{{ - 1}} \left( {\frac{{2\zeta }}{H}} \right) + \mathop \sum \nolimits_{{i = 1}}^{N} p_{i} \Phi_{{\text{i}}} \left( s \right)} \right) + \frac{H}{2} + {\text{g}}_{0} - \mathop \sum \nolimits_{{i = 1}}^{N} q_{i} \Psi_{{\text{i}}} \left( s \right)} \right)^{2} }} \\ \end{aligned} $$

(A.32)

Here, ${q}_{i}$ and ${p}_{i}$ $(i=1, 2, 3)$ are the generalized coordinates corresponding to the ${i}^{th}$ bending and torsional modes, respectively. Also, ${\Psi }_{\text{i}}(s)$ and ${\Phi }_{\text{i}}\left(s\right)$ are the eigenfunctions of the electrically tuned eigenvalue problem. The first three modes are considered for each motion direction since the natural frequencies of the higher-order bending and torsional modes are far above that of the first in-plane bending mode. This generates seven second-order nonlinearly coupled ODEs, including Eq. (1), which are then converted into 2N-space for numerical integration. A combination of the shooting and arc-length continuation schemes was scripted in MATLAB to capture the periodic orbits embedded in the MEMS's dynamics. The stability of the periodic solutions is assessed via analyzing the eigenvalues of the system's monodromy matrix.