Skip to main content
SpringerLink
Log in

New exact solutions and related dynamic behaviors of a (3+1)-dimensional generalized Kadomtsev–Petviashvili equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

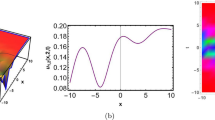
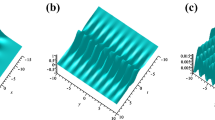
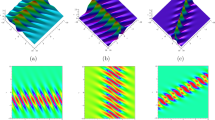
In this paper, a (3+1)-dimensional generalized Kadomtsev–Petviashvili equation is systematically investigated based on the Hirota bilinear method. The explicit N-soliton solution and the bright and dark multi-soliton solutions of it are first derived. Next, various bright and dark higher-order breather solutions, including the periodic line wave solutions, as well as the hybrid solutions composed of solitons, breathers, and periodic line waves, are proposed by virtue of the complex conjugate constraints on the parameters. Then, applying the long wave limit to the N-soliton solution, the bright and dark lump solutions and line rogue wave solutions of the (3+1)-dimensional generalized Kadomtsev–Petviashvili equation are constructed. The semi-rational solutions composed of breathers, lumps, solitons, and line rogue waves are further discussed. These new exact solutions all appear in pairs of bright and dark, which can be interpreted by the uplifts and collapses of energy. In addition, the dynamic behaviors of these exact nonlinear wave solutions are vividly demonstrated by their corresponding three-dimensional diagrams, sectional drawings, and density plots with contours.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Data availability

The data that support the findings of this article are available from the corresponding author, upon reasonable request.

References

  1. Wang, M., Zhou, Y., Li, Z.: Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys. Lett. A 216, 67–75 (1996)

    Article  Google Scholar 

  2. Fan, E.: Two new applications of the homogeneous balance method. Phys. Lett. A 265, 353–357 (2000)

    Article  MathSciNet  Google Scholar 

  3. Matveev, V.B., Salle, M.A.: Darboux Transformations and Solitons. Springer, Berlin (1991)

    Book  Google Scholar 

  4. Li, Y., Zhang, J.E.: Darboux transformations of classical Boussinesq system and its multi-soliton solutions. Phys. Lett. A 284, 253–258 (2001)

    Article  MathSciNet  Google Scholar 

  5. Gu, C., Hu, H., Zhou, Z.: Darboux Transformations in Integrable Systems: Theory and Their Applications to Geometry. Springer, Berlin (2005)

    Book  Google Scholar 

  6. Gardner, C.S., Greene, J.M., Kruskal, M.D., Miura, R.M.: Method for solving the Korteweg-deVries equation. Phys. Rev. Lett. 19, 1095–1097 (1967)

    Article  Google Scholar 

  7. Zakharov, V.E., Shabat, A.B.: A scheme for integrating the nonlinear equations of mathematical physics by the method of the inverse scattering problem. I. Funktsional. Anal. i Prilozhen. 8, 43–53 (1974)

    Google Scholar 

  8. Ablowitz, M.J., Clarkson, P.A.: Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge (1991)

    Book  Google Scholar 

  9. Ma, W.X., Abdeljabbar, A.: A bilinear B\(\ddot{a}\)cklund transformation of a (3+1)-dimensional generalized KP equation. Appl. Math. Lett. 25, 1500–1504 (2012)

    Article  MathSciNet  Google Scholar 

  10. Hietarinta, J., Joshi, N., Nijhoff, F.W.: Discrete Systems and Integrability. Cambridge University Press, Cambridge (2016)

    Book  Google Scholar 

  11. Lan, Z.Z., Gao, Y.T., Yang, J.W., et al.: Solitons, B\(\ddot{a}\)cklund transformation and Lax pair for a (2+1)-dimensional Broer–Kaup–Kupershmidt system in the shallow water of uniform depth. Commun. Nonlinear Sci. Numer. Simul. 44, 360–372 (2017)

    Article  MathSciNet  Google Scholar 

  12. Liu, S., Fu, Z., Liu, S., et al.: Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 289, 69–74 (2001)

    Article  MathSciNet  Google Scholar 

  13. Zhang, H.: Extended Jacobi elliptic function expansion method and its applications. Commun. Nonlinear Sci. Numer. Simul. 12, 627–635 (2007)

    Article  MathSciNet  Google Scholar 

  14. Hirota, R.: Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 27, 1192–1194 (1971)

    Article  Google Scholar 

  15. Hietarinta, J.: Introduction to the Hirota bilinear method. In: Kosmann-Schwarzbach, Y., Grammaticos, B., Tamizhmani, K.M. (eds.) Integrability of Nonlinear Systems, pp. 95–103. Springer, Heidelberg (1997)

    Chapter  Google Scholar 

  16. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, Cambridge (2004)

    Book  Google Scholar 

  17. Wazwaz, A.M.: Multiple-soliton solutions for the KP equation by Hirota\(^{\prime }\)s bilinear method and by the tanh-coth method. Appl. Math. Comput. 190, 633–640 (2007)

    MathSciNet  Google Scholar 

  18. Zabusky, N.J., Kruskal, M.D.: Interaction of “solitons’’ in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 15, 240–243 (1965)

    Article  Google Scholar 

  19. Freeman, N.C., Nimmo, J.J.C.: Soliton solutions of the Korteweg-de Vries and the Kadomtsev–Petviashvili equations: the Wronskian technique. Phys. Lett. A 95, 1–3 (1983)

    Article  MathSciNet  Google Scholar 

  20. Bao, W., Tang, Q., Xu, Z.: Numerical methods and comparison for computing dark and bright solitons in the nonlinear Schr\(\ddot{o}\)dinger equation. J. Comput. Phys. 235, 423–445 (2013)

    Article  MathSciNet  Google Scholar 

  21. Ren, P., Rao, J.: Bright-dark solitons in the space-shifted nonlocal coupled nonlinear Schr\(\ddot{o}\)dinger equation. Nonlinear Dyn. 108, 2461–2470 (2022)

    Article  Google Scholar 

  22. Dong, G.J., Liu, Z.Z.: Soliton resulting from the combined effect of higher order dispersion, self-steepening and nonlinearity in an optical fiber. Opt. Commun. 128, 8–14 (1996)

    Article  Google Scholar 

  23. Zhao, L.C., Li, S.C., Ling, L.: W-shaped solitons generated from a weak modulation in the Sasa–Satsuma equation. Phys. Rev. E 93, 032215 (2016)

    Article  MathSciNet  Google Scholar 

  24. Wazwaz, A.M.: Kink solutions for three new fifth order nonlinear equations. Appl. Math. Model. 38, 110–118 (2014)

    Article  MathSciNet  Google Scholar 

  25. Yuan, Y.Q., Tian, B., Liu, L., et al.: Solitons for the (2+1)-dimensional Konopelchenko–Dubrovsky equations. J. Math. Anal. Appl. 460, 476–486 (2018)

    Article  MathSciNet  Google Scholar 

  26. Kuznetsov, E.A.: Solitons in a parametrically unstable plasma. Sov. Phys. Dokl. 22, 507–508 (1977)

    Google Scholar 

  27. Ma, Y.C.: The perturbed plane-wave solutions of the cubic Schr\(\ddot{o}\)dinger equation. Stud. Appl. Math. 60, 43–58 (1979)

    Article  MathSciNet  Google Scholar 

  28. Akhmediev, N.N., Korneev, V.I.: Modulation instability and periodic solutions of the nonlinear Schr\(\ddot{o}\)dinger equation. Theor. Math. Phys. 69, 1089–1093 (1986)

    Article  Google Scholar 

  29. Ma, W.X., Zhou, R., Gao, L.: Exact one-periodic and two-periodic wave solutions to Hirota bilinear equations in (2+1) dimensions. Mod. Phys. Lett. A 24, 1677–1688 (2009)

    Article  MathSciNet  Google Scholar 

  30. Tao, Y., He, J.: Multisolitons, breathers, and rogue waves for the Hirota equation generated by the Darboux transformation. Phys. Rev. E 85, 026601 (2012)

    Article  Google Scholar 

  31. Xu, S., He, J.: The rogue wave and breather solution of the Gerdjikov–Ivanov equation. J. Math. Phys. 53, 063507 (2012)

    Article  MathSciNet  Google Scholar 

  32. Tian, S.F., Zhang, H.Q.: Riemann theta functions periodic wave solutions and rational characteristics for the (1+1)-dimensional and (2+1)-dimensional Ito equation. Chaos Soliton. Fract. 47, 27–41 (2013)

    Article  MathSciNet  Google Scholar 

  33. Petviashvili, V.I.: Equation of an extraordinary soliton. Fiz. Plazmy. 2, 469–472 (1976)

    Google Scholar 

  34. Villarroel, J., Prada, J., Estévez, P.G.: Dynamics of lump solutions in a 2+1 NLS equation. Stud. Appl. Math. 122, 395–410 (2009)

    Article  MathSciNet  Google Scholar 

  35. Ma, W.X.: Lump solutions to the Kadomtsev–Petviashvili equation. Phys. Lett. A 379, 1975–1978 (2015)

    Article  MathSciNet  Google Scholar 

  36. Ma, W.X., Zhou, Y.: Lump solutions to nonlinear partial differential equations via Hirota bilinear forms. J. Differ. Equ. 264, 2633–2659 (2018)

    Article  MathSciNet  Google Scholar 

  37. Foroutan, M., Manafian, J., Ranjbaran, A.: Lump solution and its interaction to (3+1)-D potential-YTSF equation. Nonlinear Dyn. 92, 2077–2092 (2018)

    Article  Google Scholar 

  38. Peregrine, D.H.: Water waves, nonlinear Schr\(\ddot{o}\)dinger equations and their solutions. J. Aust. Math. Soc. Ser. B. 25, 16–43 (1983)

    Article  Google Scholar 

  39. Akhmediev, N., Ankiewicz, A., Soto-Crespo, J.M.: Rogue waves and rational solutions of the nonlinear Schr\(\ddot{o}\)dinger equation. Phys. Rev. E 80, 026601 (2009)

    Article  Google Scholar 

  40. Dubard, P., Matveev, V.B.: Multi-rogue waves solutions to the focusing NLS equation and the KP-I equation. Nat. Hazards Earth Syst. Sci. 11, 667–672 (2011)

    Article  Google Scholar 

  41. Ankiewicz, A., Kedziora, D.J., Akhmediev, N.: Rogue wave triplets. Phys. Lett. A 375, 2782–2785 (2011)

    Article  Google Scholar 

  42. Guo, B., Ling, L., Liu, Q.P.: Nonlinear Schr\(\ddot{o}\)dinger equation: generalized Darboux transformation and rogue wave solutions. Phys. Rev. E 85, 026607 (2012)

    Article  Google Scholar 

  43. He, J.S., Zhang, H.R., Wang, L.H., et al.: Generating mechanism for higher-order rogue waves. Phys. Rev. E 87, 052914 (2013)

    Article  Google Scholar 

  44. Ohta, Y., Yang, J.: Rogue waves in the Davey–Stewartson I equation. Phys. Rev. E 86, 036604 (2012)

    Article  Google Scholar 

  45. Ohta, Y., Yang, J.: Dynamics of rogue waves in the Davey–Stewartson II equation. J. Phys. A: Math. Theor. 46, 105202 (2013)

    Article  MathSciNet  Google Scholar 

  46. Bandelow, U., Akhmediev, N.: Persistence of rogue waves in extended nonlinear Schr\(\ddot{o}\)dinger equations: Integrable Sasa–Satsuma case. Phys. Lett. A 376, 1558–1561 (2012)

    Article  Google Scholar 

  47. Chen, S.: Twisted rogue-wave pairs in the Sasa–Satsuma equation. Phys. Rev. E 88, 023202 (2013)

    Article  Google Scholar 

  48. Mu, G., Qin, Z.: Dynamic patterns of high-order rogue waves for Sasa–Satsuma equation. Nonlinear Anal. Real World Appl. 31, 179–209 (2016)

    Article  MathSciNet  Google Scholar 

  49. Akhmediev, N., Ankiewicz, A., Taki, M.: Waves that appear from nowhere and disappear without a trace. Phys. Lett. A 373, 675–678 (2009)

    Article  Google Scholar 

  50. Bludov, Y.V., Konotop, V.V., Akhmediev, N.: Matter rogue waves. Phys. Rev. A 80, 033610 (2009)

    Article  Google Scholar 

  51. Bludov, Y.V., Konotop, V.V., Akhmediev, N.: Vector rogue waves in binary mixtures of Bose–Einstein condensates. Eur. Phys. J. Spec. Top. 185, 169–180 (2010)

    Article  Google Scholar 

  52. Solli, D.R., Ropers, C., Koonath, P., et al.: Optical rogue waves. Nature 450, 1054–1057 (2007)

    Article  Google Scholar 

  53. Stenflo, L., Marklund, M.: Rogue waves in the atmosphere. J. Plasma Phys. 76, 293–295 (2010)

    Article  Google Scholar 

  54. El-Awady, E.I., Moslem, W.M.: On a plasma having nonextensive electrons and positrons: Rogue and solitary wave propagation. Phys. Plasmas 18, 082306 (2011)

    Article  Google Scholar 

  55. Rao, J., Zhang, Y., Fokas, A.S., et al.: Rogue waves of the nonlocal Davey–Stewartson I equation. Nonlinearity 31, 4090–4107 (2018)

    Article  MathSciNet  Google Scholar 

  56. Cao, Y., Cheng, Y., Malomed, B.A., He, J.: Rogue waves and lumps on the nonzero background in the PT-symmetric nonlocal Maccari system. Stud. Appl. Math. 147, 694–723 (2021)

    Article  MathSciNet  Google Scholar 

  57. Tian, S.F., Ma, P.L.: On the quasi-periodic wave solutions and asymptotic analysis to a (3+1)-dimensional generalized Kadomtsev–Petviashvili equation. Commun. Theor. Phys. 62, 245–258 (2014)

    Article  MathSciNet  Google Scholar 

  58. Hu, C.C., Tian, B., Yin, H.M., et al.: Dark breather waves, dark lump waves and lump wave-soliton interactions for a (3+1)-dimensional generalized Kadomtsev–Petviashvili equation in a fluid. Comput. Math. Appl. 78, 166–177 (2019)

    Article  MathSciNet  Google Scholar 

  59. Wang, M., Tian, B., Sun, Y., et al.: Mixed lump-stripe, bright rogue wave-stripe, dark rogue wave-stripe and dark rogue wave solutions of a generalized Kadomtsev–Petviashvili equation in fluid mechanics. Chin. J. Phys. 60, 440–449 (2019)

    Article  MathSciNet  Google Scholar 

  60. Yu, W., Zhang, H., Zhou, Q., Biswas, A., et al.: The mixed interaction of localized, breather, exploding and solitary wave for the (3+1)-dimensional Kadomtsev–Petviashvili equation in fluid dynamics. Nonlinear Dyn. 100, 1611–1619 (2020)

  61. Ma, W.X.: Complexiton solutions to the Korteweg-de Vries equation. Phys. Lett. A 301, 35–44 (2002)

    Article  MathSciNet  Google Scholar 

  62. Novikov, S.P.: The periodic problem for the Korteweg-de Vries equation. Funct. Anal. Appl. 8, 54–66 (1974)

    MathSciNet  Google Scholar 

  63. Ma, W.X.: Comment on the 3+1 dimensional Kadomtsev–Petviashvili equations. Commun. Nonlinear Sci. Numer. Simul. 16, 2663–2666 (2011)

    Article  MathSciNet  Google Scholar 

  64. Ablowitz, M.J., Satsuma, J.: Solitons and rational solutions of nonlinear evolution equations. J. Math. Phys. 19, 2180–2186 (1978)

    Article  MathSciNet  Google Scholar 

  65. Rao, J., Porsezian, K., He, J.: Semi-rational solutions of the third-type Davey–Stewartson equation. Chaos 27, 083115 (2017)

    Article  MathSciNet  Google Scholar 

  66. Rao, J., Cheng, Y., He, J.: Rational and semirational solutions of the nonlocal Davey–Stewartson equations. Stud. Appl. Math. 139, 568–598 (2017)

    Article  MathSciNet  Google Scholar 

  67. Cao, Y., He, J., Mihalache, D.: Families of exact solutions of a new extended (2+1)-dimensional Boussinesq equation. Nonlinear Dyn. 91, 2593–2605 (2018)

    Article  Google Scholar 

  68. Cao, Y., Rao, J., Mihalache, D., He, J.: Semi-rational solutions for the (2+1)-dimensional nonlocal Fokas system. Appl. Math. Lett. 80, 27–34 (2018)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work is supported by the Zhejiang Provincial Natural Science Foundation of China under Grant No.LY24A010002, the National Natural Science Foundation of China under Grant No. 1211153003, the Natural Science Foundation of Ningbo under Grant No. 2023J126, K. C. Wong Magna Fund in Ningbo University.

Funding

The authors have not disclosed any funding.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Ningbo University, Ningbo, 315211, Zhejiang, People’s Republic of China

    Lingna Ying & Maohua Li

  2. School of Science, Ningbo University of Technology, Ningbo, 315210, Zhejiang, People’s Republic of China

    Yafeng Shi

Authors
  1. Lingna Ying
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Maohua Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yafeng Shi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Maohua Li.

Ethics declarations

Conflict of interest

The authors declare that they have no Conflict of interest.

Ethical approval

The authors declare that they comply with ethical standards.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ying, L., Li, M. & Shi, Y. New exact solutions and related dynamic behaviors of a (3+1)-dimensional generalized Kadomtsev–Petviashvili equation. Nonlinear Dyn (2024). https://doi.org/10.1007/s11071-024-09539-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11071-024-09539-2

Keywords

Mathematics Subject Classification

Search

Navigation