Skip to main content
SpringerLink
Log in

Multi-soliton solutions of a variable coefficient Schrödinger equation derived from vorticity equation

  • Review
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

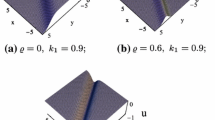
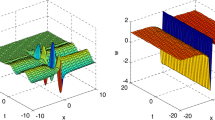
A variable coefficient Schrödinger equation which is derived by using the multi-scale expansion and coordinate expansion transformation method from nonlinear inviscid barotropic nondivergent vorticity equation in a \(\beta \)-plane is discussed in this paper. It is different from the previous model that the background basic flow is assumed as a function of time t. Then, the bilinear forms are obtained based on a transformation. By using the Hirota bilinear method, exact analytical solutions to the Schrödinger equation are achieved. These solutions include single-soliton, two-soliton and three-soliton solutions, whose interactions have been presented in the form of 3-d solid figure or density graphic to describe the dynamic characteristics, and might help to describe Rossby waves more suitable. Furthermore, the effects on solitons of coefficients except which relate to the dispersion relation of the model are discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data availability

All data are included in this published article. This article has no other associated data.

References

  1. Tang, X.Y., Gao, Y., Huang, F., Lou, S.Y.: Variable coefficient nonlinear systems derived from an atmospheric dynamical system. Chin. Phys. B 18, 4622 (2009)

    Google Scholar 

  2. Luo, D.H.: Blocking Nonlinear Dynamics. China Meteorological Press, Beijing (2000). (in Chinese)

    Google Scholar 

  3. Tang, X.Y., Liang, Z.F., Hao, X.Z.: Nonlinear waves of a nonlocal modified KdV equation in the atmospheric and oceanic dynamical system. Commun. Nonlinear Sci. Numer. Simul. 60, 62–71 (2018)

    MathSciNet  Google Scholar 

  4. Yu, X., Gao, Y.T., Sun, Z.Y., Liu, Y.: Solitonic propagation and interaction for a generalized variable-coefficient forced Korteweg–de Vries equation in fluids. Phys. Rev. E 83, 056601 (2011)

    Google Scholar 

  5. Yu, X., Gao, Y.T., Sun, Z.Y., Liu, Y.: Wronskian solutions and integrability for a generalized variable-coefficient forced Korteweg–de Vries equation in fluids. Nonlinear Dyn. 67, 1023–1030 (2012)

    MathSciNet  Google Scholar 

  6. Yu, X., Sun, Z.Y., Zhou, K.W., Shen, Y.J.: Spacial inhomogeneity and nonlinear tunneling for the forced KdV equation. Appl. Math. Lett. 75, 30–36 (2018)

    MathSciNet  Google Scholar 

  7. Tian, S.F., Zhang, H.Q.: On the integrability of a generalized variable-coefficient forced Korteweg–de Vries equation in fluids. Stud. Appl. Math. 132, 212–246 (2014)

    MathSciNet  Google Scholar 

  8. Luo, D.H.: Envelope solitary Rossby waves and modulational instabilities of uniform Rossby wave trains in two space dimensions. Wave Motion 24, 315–325 (1996)

    MathSciNet  Google Scholar 

  9. Ablowitz, M.J., Musslimani, Z.H.: Integrable nonlocal nonlinear Schrödinger equation. Phys. Rev. Lett. 110, 064105 (2013)

    Google Scholar 

  10. Tan, B.K., Boyd, J.P.: Coupled-mode envelope solitary waves in a pair of cubic Schrödinger equations with cross modulation: analytical solution and collisions with application to Rossby waves. Chaos Solitons Fractals 11, 1113–1129 (2000)

    MathSciNet  Google Scholar 

  11. Akhmediev, N., Ankiewicz, A., Soto-Crespo, J.M.: Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys. Rev. E 80, 026601 (2009)

    Google Scholar 

  12. Ankiewicz, A., Wang, Y., Wabnitz, S., Akhmediev, N.: Extended nonlinear Schrödinger equation with higher-order odd and even terms and its rogue wave solutions. Phys. Rev. E 89, 012907 (2014)

    Google Scholar 

  13. Wazwaz, A.M., Kaur, L.: Optical solitons for nonlinear Schrödinger equation in normal dispersive regimes. Optik 184, 428–435 (2019)

    Google Scholar 

  14. Gadzhimuradov, T.A., Agalarov, A.M., Radha, R., Tamil Arasan, B.: Dynamics of solitons in the fourth-order nonlocal nonlinear Schrödinger equation. Nonlinear Dyn. 99, 1295–1300 (2020)

    Google Scholar 

  15. Liu, S.Z., Zhou, Q., Biswas, A., Liu, W.J.: Phase-shift controlling of three solitons in dispersion-decreasing fibers. Nonlinear Dyn. 98, 395–401 (2019)

    Google Scholar 

  16. Chowdury, A., Krolikowski, W., Akhmediev, N.: Breather solutions of fourth-order nonlinear Schrödinger equation in the degenerate, soliton, and rogue wave limits. Phys. Rev. E 96, 042209 (2017)

    MathSciNet  Google Scholar 

  17. Wazwaz, A.M., Albalawi, W., El-Tantawy, S.A.: Optical envelope soliton solutions for coupled nonlinear Schrödinger equations applicable to high birefringence fibers. Optik 255, 168673 (2022)

    Google Scholar 

  18. Luo, D.H., Chen, X.D., Dai, A.G., Simmonds, I.: Changes in atmospheric blocking circulations linked with winter arctic warming: a new perspective. J. Clim. 31, 7661–7678 (2018)

    Google Scholar 

  19. Fu, C., Lu, C.N., Yang, H.W.: Time-space fractional (2+1) dimensional nonlinear Schrödinger equation for envelope gravity waves in baroclinic atmosphere and conservation laws as well as exact solutions. Adv. Differ. Equ. 2018, 56 (2018)

    Google Scholar 

  20. Wang, C., Li, J.J., Yang, H.W.: Modulation instability analysis of Rossby waves based on (2+1) dimensional high-order Schrödinger equation. Commun. Theor. Phys. 74, 075002 (2022)

    Google Scholar 

  21. Xu, L.Y., Yin, X.J., Cao, N., Bai, S.T.: Soliton propagation for a coupled Schrödinger equation describing Rossby waves. Chin. Phys. B 32, 070202 (2023)

    Google Scholar 

  22. Yin, X.J., Xu, L.Y., Yang, L.G.: Evolution and interaction of soliton solutions of Rossby waves in geophysical fluid mechanics. Nonlinear Dyn. 111, 12433–12445 (2023)

    Google Scholar 

  23. Luo, D., Cha, J., Zhong, L.H., Dai, A.G.: A nonlinear multiscale interaction model for atmospheric blocking: the eddy-blocking matching mechanism. Q. J. R. Meteorol. Soc. 140, 1785–1808 (2014)

    Google Scholar 

  24. Yin, X.J., Yang, L.G., Liu, Q.S., Su, J.M., Wu, G.R.: Structure of equatorial envelope Rossby solitary waves with complete Coriolis force and the external source. Chaos Solitons Fractals 111, 68–74 (2018)

    MathSciNet  Google Scholar 

  25. Zhang, R.G., Liu, Q.S., Yang, L.G., Song, J.: Nonlinear planetary-synoptic wave interaction under generalized beta effect and its solutions. Chaos Solitons Fractals 122, 270–280 (2019)

    MathSciNet  Google Scholar 

  26. Wazwaz, A.M.: New (3+1)-dimensional Painlevé integrable fifth-order equation with third-order temporal dispersion. Nonlinear Dyn. 106, 891–897 (2021)

    Google Scholar 

  27. Wazwaz, A.M.: Painlevé integrability and lump solutions for two extended (3+1)- and (2+1)-dimensional Kadomtsev–Petviashvili equations. Nonlinear Dyn. 111, 3623–3632 (2023)

    Google Scholar 

  28. Liu, Y., Zhang, W.X., Ma, W.X.: Riemann–Hilbert problems and soliton solutions for a generalized coupled Sasa-Satsuma equation. Commun. Nonlinear Sci. Numer. Simul. 118, 107052 (2023)

    MathSciNet  Google Scholar 

  29. Zhou, H.J., Chen, Y.: High-order soliton solutions and their dynamics in the inhomogeneous variable coefficients Hirota equation. Commun. Nonlinear Sci. Numer. Simul. 120, 107149 (2023)

    MathSciNet  Google Scholar 

  30. Guo, J.H., Guo, R.: Soliton solutions for two kinds of fourth-order nonlinear nonlocal Schrödinger equations. Commun. Nonlinear Sci. Numer. Simul. 117, 106940 (2023)

    Google Scholar 

  31. Zhao, X.J., Guo, R., Hao, H.Q.: N-fold Darboux transformation and discrete soliton solutions for the discrete Hirota equation. Appl. Math. Lett. 75, 114–120 (2018)

    MathSciNet  Google Scholar 

  32. Guan, X., Liu, W.J., Zhou, Q., Biswas, A.: Darboux transformation and analytic solutions for a generalized super-NLS-mKdV equation. Nonlinear Dyn. 98, 1491–1500 (2019)

    Google Scholar 

  33. Zhang, R.F., Bilige, S.: Bilinear neural network method to obtain the exact analytical solutions of nonlinear partial differential equations and its application to p-gBKP equation. Nonlinear Dyn. 95, 3041–3048 (2019)

    Google Scholar 

  34. Zhang, R.F., Li, M.C., Mohammed, A., Zheng, F.C., Lan, Z.Z.: Generalized lump solutions, classical lump solutions and rogue waves of the (2+1)-dimensional Caudrey–Dodd–Gibbon–Kotera–Sawada-like equation. Appl. Math. Comput. 403, 126201 (2021)

    MathSciNet  Google Scholar 

  35. Zhang, R.F., Li, M.C., Gan, J.Y., Li, Q., Lan, Z.Z.: Novel trial functions and rogue waves of generalized breaking soliton equation via bilinear neural network method. Chaos Solitons Fractals 154, 111692 (2022)

    MathSciNet  Google Scholar 

  36. Zhang, R.F., Li, M.C., Cherraf, A., Vadyala, S.R.: The interference wave and the bright and dark soliton for two integro-differential equation by using BNNM. Nonlinear Dyn. 111, 8637–8646 (2023)

    Google Scholar 

  37. Zhang, R.F., Li, M.C.: Bilinear residual network method for solving the exactly explicit solutions of nonlinear evolution equations. Nonlinear Dyn. 108, 521–531 (2022)

    Google Scholar 

  38. Chen, J., Chen, Y., Feng, B.F., Maruno, K.: General mixed multi-soliton solutions to one-dimensional multicomponent Yajima–Oikawa system. J. Phys. Soc. Jpn. 84, 074001 (2015)

    Google Scholar 

  39. Pu, J.C., Li, J., Chen, Y.: Soliton, breather, and rogue wave solutions for solving the nonlinear Schrödinger equation using a deep learning method with physical constraints. Chin. Phys. B 30, 060202 (2021)

    Google Scholar 

  40. Akinyemi, L., Akpan, U., Veeresha, P., Rezazadeh, H., Inc, M.: Computational techniques to study the dynamics of generalized unstable nonlinear Schrödinger equation. J. Ocean Eng. Sci. (2022). https://doi.org/10.1016/j.joes.2022.02.011

  41. Feng, Z.: Traveling wave behavior for a generalized fisher equation. Chaos Solitons Fractals 38, 481–488 (2008)

    MathSciNet  Google Scholar 

  42. Lü, X., Hua, Y.F., Chen, S.J., Tang, X.F.: Integrability characteristics of a novel (2+1)-dimensional nonlinear model: Painlevé analysis, soliton solutions, Bäcklund transformation, Lax pair and infinitely many conservation laws. Commun. Nonlinear Sci. Numer. Simul. 95, 105612 (2021)

    Google Scholar 

  43. Lü, X., Chen, S.J.: Interaction solutions to nonlinear partial differential equations via Hirota bilinear forms: one-lump-multi-stripe and one-lump-multi-soliton types. Nonlinear Dyn. 103, 947–977 (2021)

    Google Scholar 

  44. Yin, Y.H., Lü, X., Ma, W.X.: Bäcklund transformation, exact solutions and diverse interaction phenomena to a (3+1)-dimensional nonlinear evolution equation. Nonlinear Dyn. 108, 4181–4194 (2022)

    Google Scholar 

  45. Chen, S.J., Lü, X.: Lump and lump-multi-kink solutions in the (3+1)-dimensions. Commun. Nonlinear Sci. Numer. Simul. 109, 106103 (2022)

    MathSciNet  Google Scholar 

  46. Bi, K., Hao, H.Q., Zhang, J.W., Guo, R.: Soliton, breather-like and dark-soliton-breather-like solutions for the coupled long-wave-short-wave system. Nonlinear Dyn. 108, 543–554 (2022)

    Google Scholar 

  47. Zhang, X., Chen, Y., Zhang, Y.: Breather, lump and X soliton solutions to nonlocal KP equation. Comput. Math. Appl. 74, 2341–2347 (2017)

    MathSciNet  Google Scholar 

  48. Sun, Y.: Analytic study on several nonlinear models in optical fiber communications, fluids and other fields. Ph.D. Dissertation, Beijing University of Posts and Telecommunications, Beijing (2021) (in Chinese)

Download references

Funding

This work is supported by the National Natural Science Foundation of China (12362027 and 12361069), the Inner Mongolia Autonomous Region’s Natural Science Foundation (2022QN01003), the foundational research fund in the basic sciences of Inner Mongolia Agricultural University (JC2021001), the Inner Mongolia Autonomous Region’s Program for Young Talents in Science and Technology (NJYT23099 and NMGIRT2208), the Inner Mongolia Agricultural University’s Program for Improving the Scientific Research Capability of Youth Teachers (BR220126).

Author information

Authors and Affiliations

  1. College of Science, Inner Mongolia Agriculture University, Hohhot, 010018, China

    Liyang Xu, Xiaojun Yin, Na Cao & Shuting Bai

Authors
  1. Liyang Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaojun Yin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Na Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shuting Bai
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

L.X. helped in methodology, writing—original draft. X.Y. contributed to conceptualization, writing—reviewing and editing. N.C. was involved in validation. S.B. helped in software.

Corresponding author

Correspondence to Xiaojun Yin.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, L., Yin, X., Cao, N. et al. Multi-soliton solutions of a variable coefficient Schrödinger equation derived from vorticity equation. Nonlinear Dyn 112, 2197–2208 (2024). https://doi.org/10.1007/s11071-023-09158-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-023-09158-3

Keywords

Search

Navigation