Skip to main content
SpringerLink
Log in

Asymptotic analysis of circular motions of base- and length-parametrically excited pendula

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

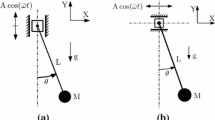
The regular circular motions of parametrically excited pendula are analyzed via the Multiple Scale Perturbation Method. Two different cases, object of discussions in the literature, are considered, namely the base-excited pendulum (BEP) and the variable-length pendulum (VLP), which exhibit different behaviors, hitherto unexplained. Under the hypothesis that the parametric excitation is of large frequency, the problem is recast in the form of a perturbation of a singular linear differential operator, admitting a double-zero eigenvalue, where the perturbation parameter is identified in the amplitude of the parametric excitation. Similarly to the linear algebraic eigenvalue problem around such a degenerate point, the asymptotic method calls for using fractional power expansions of the perturbation parameter, for both the state variables and the time-derivative operator. However, while the perturbation appears to be regular in the BEP, so that fractional series apply, it is singular in the VLP, so that such expansions degenerate in integer powers. As a consequence, the BEP is more prone to execute circular motions, in the sense that a lower excitation amplitude is required, in comparison with the VLP. Such a result is confirmed by common experiences in the real world, examples of which are given. On the other hand, the VLP admits motions with different angular velocities, while the BEP just admits one velocity, at least to within the order of the asymptotic solution carried out here. The approach followed is believed to give a satisfactory mathematical explanation of the different behaviors of the two systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Data Availability

The data that support the findings of this study will be made available upon request.

References

  1. Abbas Hassan, S., Osman, T., Khattab, A., Arafa, M., Abdelnaby, M.A.: Design of a self-tunable, variable-length pendulum for harvesting energy from rotational motion. J. Vibroeng. 22(6), 1309–1325 (2020)

    Article  Google Scholar 

  2. Dotti, F.E., Virla, J.N.: Nonlinear dynamics of the parametric pendulum with a view on wave energy harvesting applications. J. Comput. Nonlinear Dyn. 16(6), 061007 (2021)

    Article  Google Scholar 

  3. Alevras, P., Brown, I., Yurchenko, D.: Experimental investigation of a rotating parametric pendulum. Nonlinear Dyn. 81, 201–213 (2015)

    Article  Google Scholar 

  4. Yurchenko, D., Alevras, P.: Parametric pendulum based wave energy converter. Mech. Syst. Signal Process. 99, 504–515 (2018)

    Article  Google Scholar 

  5. Stilling, D.S., Szyszkowski, W.: Controlling angular oscillations through mass reconfiguration: a variable length pendulum case. Int. J. Non-Linear Mech. 37(1), 89–99 (2002)

    Article  Google Scholar 

  6. Reguera, F., Dotti, F.E., Machado, S.P.: Rotation control of a parametrically excited pendulum by adjusting its length. Mech. Res. Commun. 72, 74–80 (2016)

    Article  Google Scholar 

  7. Tusset, A., Janzen, F., Piccirillo, V., Rocha, R., Balthazar, J., Litak, G.: On nonlinear dynamics of a parametrically excited pendulum using both active control and passive rotational (MR) damper. J. Vib. Control 24(9), 1587–1599 (2018)

    Article  MathSciNet  Google Scholar 

  8. Stein, A., Parcic, T., Singh, T.: From playground swings to sway control of cranes: an active pendulum experiment. Int. J. Mech. Eng. Ed. (2023). https://doi.org/10.1177/030641902311593

    Article  Google Scholar 

  9. Anderle, M., Appeltans, P., Čelikovskỳ, S., Michiels, W., Vyhlídal, T.: Controlling the variable length pendulum: analysis and Lyapunov based design methods. J. Frankl. Inst. 359(3), 1382–1406 (2022)

    Article  MathSciNet  Google Scholar 

  10. Yakubu, G., Olejnik, P., Awrejcewicz, J.: On the modeling and simulation of variable-length pendulum systems: A review. Arch. Comput. Methods Eng. 29(4), 2397–2415 (2022)

    Article  MathSciNet  Google Scholar 

  11. Seyranian, A.: The swing: parametric resonance. J. Appl. Math. Mech. 68(5), 757–764 (2004)

    Article  MathSciNet  Google Scholar 

  12. Zevin, A., Filonenko, L.: A qualitative investigation of the oscillations of a pendulum with a periodically varying length and a mathematical model of a swing. J. Appl. Math. Mech. 71(6), 892–904 (2007)

    Article  MathSciNet  Google Scholar 

  13. Pinsky, M., Zevin, A.: Oscillations of a pendulum with a periodically varying length and a model of swing. Int. J Non-linear Mech. 34(1), 105–109 (1999)

    Article  MathSciNet  Google Scholar 

  14. Aslanov, V.S.: Stability of a pendulum with a moving mass: the averaging method. J. Sound Vib. 445, 261–269 (2019)

    Article  Google Scholar 

  15. Yang, H., Han, X.: Existence of periodic solutions for the forced pendulum equations of variable length. Qual. Theory of Dyn. Syst. 22(1), 20 (2023)

    Article  MathSciNet  Google Scholar 

  16. Belyakov, A.O., Seyranian, A.P., Luongo, A.: Dynamics of the pendulum with periodically varying length. Phys. D Nonlinear Phenom. 238(16), 1589–1597 (2009)

    Article  Google Scholar 

  17. Wright, J.A., Bartuccelli, M., Gentile, G.: Comparisons between the pendulum with varying length and the pendulum with oscillating support. J. Math. Anal. Appl. 449(2), 1684–1707 (2017)

    Article  MathSciNet  Google Scholar 

  18. Belyakov, A.O.: On rotational solutions for elliptically excited pendulum. Phys. Lett. A 375(25), 2524–2530 (2011)

    Article  MathSciNet  Google Scholar 

  19. Clifford, M., Bishop, S.: Rotating periodic orbits of the parametrically excited pendulum. Phys. Lett. A 201(2–3), 191–196 (1995)

    Article  MathSciNet  Google Scholar 

  20. Xu, X., Wiercigroch, M., Cartmell, M.: Rotating orbits of a parametrically-excited pendulum. Chaos Solitons Fractals 23(5), 1537–1548 (2005)

    Article  Google Scholar 

  21. Xu, X., Wiercigroch, M.: Approximate analytical solutions for oscillatory and rotational motion of a parametric pendulum. Nonlinear Dyn. 47, 311–320 (2007)

    Article  MathSciNet  Google Scholar 

  22. Lenci, S., Pavlovskaia, E., Rega, G., Wiercigroch, M.: Rotating solutions and stability of parametric pendulum by perturbation method. J. Sound Vib. 310(1–2), 243–259 (2008)

    Article  Google Scholar 

  23. Luongo, A., Ferretti, M., Di Nino, S.: Stability and Bifurcation of Structures: Statical and Dynamical Systems. Springer, Berlin (2023)

    Book  Google Scholar 

  24. Luongo, A., Paolone, A., Egidio, A.D.: Sensitivities and linear stability analysis around a double-zero eigenvalue. AIAA J. 38(4), 702–710 (2000)

    Article  Google Scholar 

  25. Bogoliubov, N., Mitropolsky, Y.: Asymptotic Methods in the Theory of Nonlinear Oscillations (1961)

  26. Arkhipova, I.M., Luongo, A., Seyranian, A.P.: Vibrational stabilization of the upright statically unstable position of a double pendulum. J. Sound Vib. 331(2), 457–469 (2012)

    Article  Google Scholar 

  27. Arkhipova, I.M., Luongo, A.: Stabilization via parametric excitation of multi-dof statically unstable systems. Commun. Nonlinear Sci. Numer. Simul. 19(10), 3913–3926 (2014)

    Article  MathSciNet  Google Scholar 

  28. Thomsen, J.J.: Theories and experiments on the stiffening effect of high-frequency excitation for continuous elastic systems. J. Sound Vib. 260(1), 117–139 (2003)

  29. Thomsen, J.J.: Effective properties of mechanical systems under high-frequency excitation at multiple frequencies. J. Sound Vib. 311(3–5), 1249–1270 (2008)

    Article  Google Scholar 

  30. Shishkina, E., Blekhman, I., Cartmell, M., Gavrilov, S.: Application of the method of direct separation of motions to the parametric stabilization of an elastic wire. Nonlinear Dyn. 54, 313–331 (2008)

    Article  MathSciNet  Google Scholar 

  31. Otterbein, S.: Stabilisierung des n-pendels und der indische seiltrick. Arch. Ration. Mech. Anal. 78, 381–393 (1982)

    Article  MathSciNet  Google Scholar 

  32. Champneys, A., Fraser, W.: The ‘Indian rope trick’ for a parametrically excited flexible rod: linearized analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 456(1995), 553–570 (2000)

    Article  MathSciNet  Google Scholar 

  33. Mullin, T., Champneys, A., Barrie Fraser, W., Galan, J., Acheson, D.: The ‘Indian wire trick’ via parametric excitation: a comparison between theory and experiment. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 459(2031), 539–546 (2003)

    Article  MathSciNet  Google Scholar 

  34. Blekhman, I.: Selected Topics in Vibrational Mechanics, vol. 11. World scientific, Singapore (2004)

    Google Scholar 

  35. Galan, J., Fraser, W., Acheson, D., Champneys, A.: The parametrically excited upside-down rod: an elastic jointed pendulum model. J. Sound Vib. 280(1–2), 359–377 (2005)

    Article  Google Scholar 

  36. Nayfeh, A.: Perturbation Methods. Wiley, New York (1973)

    Google Scholar 

  37. Luongo, A., Di Egidio, A., Paolone, A.: Multiple-timescale analysis for bifurcation from a multiple-zero eigenvalue. AIAA J. 41(6), 1143–1150 (2003)

    Article  Google Scholar 

  38. Luongo, A.: On the use of the multiple scale method in solving ‘difficult’bifurcation problems. Math. Mech. Solids 22(5), 988–1004 (2017)

    Article  MathSciNet  Google Scholar 

  39. Luongo, A., Di Egidio, A., Paolone, A.: Multiscale analysis of defective multiple-hopf bifurcations. Comput. Struct. 82(31–32), 2705–2722 (2004)

    Article  MathSciNet  Google Scholar 

Download references

Funding

The authors have not disclosed any funding.

Author information

Authors and Affiliations

  1. Department of Civil, Construction-Architectural and Environmental Engineering, University of L’ Aquila, 67100, L’Aquila, Italy

    A. Luongo

  2. Department of Architecture, University of Roma Tre, 00185, Roma, Italy

    A. Casalotti

Authors
  1. A. Luongo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Casalotti
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Luongo.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Luongo, A., Casalotti, A. Asymptotic analysis of circular motions of base- and length-parametrically excited pendula. Nonlinear Dyn 112, 757–773 (2024). https://doi.org/10.1007/s11071-023-09112-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-023-09112-3

Keywords

Search

Navigation