Skip to main content
SpringerLink
Log in

Periodic solution and asymptotic behavior of the three-dimensional sixth-order Boussinesq equation in shallow water waves

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

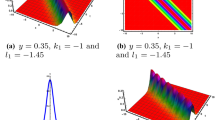
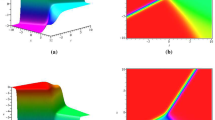
In this study, the surface wave in inviscid fluid was analyzed. Starting from Euler equation and mass conservation equation, coupled with a set of boundary conditions, the equations obtained by dimensionless method contain two parameters: amplitude parameter \(\alpha \) and shallowness parameter \(\beta \). Using double-series perturbation analysis and scale transformation, the (\(2+1\))-dimensional sixth-order Boussinesq equation is derived for the first time. Based on the Lie group analysis, the generator and the single-parameter invariant group of the new Boussinesq equation are obtained. The conservation laws of the equation are given by using the generator and the adjoint equation. Using Hirota’s bilinear method, we obtain the bilinear equation and residual equation. The existence of the residual equation shows the incomplete integrability of the Boussinesq equation. And judgment conditions for linear stability and orbital stability are obtained. The one-soliton solution and two-soliton solutions are obtained from the Hirota bilinear form. With the Riemann theta function \(\theta _3(\phi ,\;q)\), we study the periodic wave solution. When \(q \rightarrow 0\), it is proved that the periodic solution can be reduced to the one-soliton solution in the limit case based on the asymptotic behavior. Finally, using the graph, it is found that the periodic wave solution can be regarded as the parallel superposition of the one-soliton solution, and the effects of amplitude parameter \(\alpha \) and shallowness parameter \(\beta \) on the amplitude of surface wave are analyzed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Data availability

The data sets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

  1. Xu, H.Z., Wang, Y., Liu, Z.Q., McWilliams, J.C., Gan, J.: Insight into the dynamics of the radiating internal tide associated with the Kuroshio current. J. Geophys. Res.-Oceans. (2021). https://doi.org/10.1029/2020JC017018

    Article  Google Scholar 

  2. Zhao, C., Xu, H.Z., Robertson, R., Qun, L., Wang, Y., Yin, B.S.: The three dimensional internal tide radiation and dissipation in the Mariana Arc-Trench system. J. Geophys. Res. Oceans. (2021). https://doi.org/10.1029/2020JC016502

    Article  Google Scholar 

  3. Johnson, R.S.: A Two-dimensional Boussinesq equation for water waves and some of its solutions. J. Fluid Mech. 323(1), 65–78 (2021)

    MathSciNet  Google Scholar 

  4. Wazwaz, A.M.: Multiple-soliton solutions for the ninth-order KdV equation and sixth-order Boussinesq equation. Appl. Math. Comput. 203(1), 277–283 (2008)

    MathSciNet  Google Scholar 

  5. Seadawy, A.R., El-Kalaawy, O.H., Aldenari, R.B.: Water wave solutions of Zufiria’s higher-order Boussinesq type equations and its stability. Appl. Math. Comput. 280, 57–71 (2016)

    MathSciNet  Google Scholar 

  6. Zhang, R.G., Liu, Q.S., Yang, L.G.: New model and dynamics of higher-dimensional nonlinear Rossby waves. Mod. Phys. Lett. B (2019). https://doi.org/10.1142/S0217984919503421

    Article  MathSciNet  Google Scholar 

  7. Zhang, J.Q., Zhang, R.G., Yang, L.G., Liu, Q.S., Chen, L.G.: Coherent structures of nonlinear barotropic-baroclinic interaction in unequal depth two-layer model. Appl. Math. Comput. 408, 126347 (2021)

    MathSciNet  Google Scholar 

  8. Chen, L.G., Gao, F.F., Li, L.L., Yang, L.G.: A new three dimensional dissipative Boussinesq equation for Rossby waves and its multiple soliton solutions. Results Phys. 26, 104389 (2021)

    Article  Google Scholar 

  9. Daripa, P.: Higher-order Boussinesq equations for two-way propagation of shallow water waves. Eur. J. Mech. B-Fluid 25(6), 1008–1021 (2006)

    Article  MathSciNet  Google Scholar 

  10. Dash, R.K., Daripa, P.: Analytical and numerical studies of a singularly perturbed Boussinesq equation. Appl. Math. Comput. 126(1), 1–30 (2002)

    MathSciNet  Google Scholar 

  11. Constantin, A., Johnson, R.S.: On the non-dimensionalisation, scaling and resulting interpretation of the classical governing equations for water waves. J. Nonlinear Math. Phy. 15, 58–73 (2008)

    Article  MathSciNet  Google Scholar 

  12. Tian, C.: Applications of Lie Groups to Differential Equations, pp. 182–278. Science and Technology Press, Beijing (2001)

    Google Scholar 

  13. Ibragimov, N.H.: Integrating factors, adjoint equations and Lagrangians. J. Math. Anal. Appl. 318(2), 742–757 (2006)

    Article  MathSciNet  Google Scholar 

  14. Ibragimov, N.H.: A new conservation theorem. J. Math. Anal. Appl. 333(1), 311–328 (2007)

    Article  MathSciNet  Google Scholar 

  15. Ibragimov, N.H.: Nonlinear self-adjointness and conservation laws. J. Phys. A-Math. Theor. 44(43), 432002 (2011)

    Article  Google Scholar 

  16. Khalique, C.M., Moleleki, L.D.: A (3+1)-dimensional generalized BKP-Boussinesq equation: Lie group approach. Results Phys. 13, 102239 (2019)

    Article  Google Scholar 

  17. Tian, S.F.: Lie symmetry analysis, conservation laws and solitary wave solutions to a fourth-order nonlinear generalized Boussinesq water wave equation. Appl. Math. Lett. 100, 106056 (2020)

    Article  MathSciNet  Google Scholar 

  18. Wang, J., Zhang, R.G., Yang, L.G.: A Gardner evolution equation for topographic Rossby waves and its mechanical analysis. Appl. Math. Comput. 385, 125426 (2020)

    MathSciNet  Google Scholar 

  19. Helal, M.A., Seadawy, A.R., Zekry, M.: Stability analysis of solutions for the sixth-order nonlinear Boussinesq water wave equations in two-dimensions and its applications. Chin. J. Phys. 55(2), 378–385 (2017)

    Article  Google Scholar 

  20. Gao, L.N., Zi, Y.Y., Yin, Y.H., Ma, W.X., Lü, X.: Xing, Bäcklund transformation, multiple wave solutions and lump solutions to a (3+1)-dimensional nonlinear evolution equation. Nonlinear Dyn. 89, 2233–2240 (2017)

    Article  Google Scholar 

  21. Yong, X.L., Fan, Y.J., Huang, Y.H., Ma, W.X., Tian, J.: Darboux transformation and solitons for an integrable nonautonomous nonlinear integro-differential Schrödinger equation. Mod. Phys. Lett. B 31(30), 1750276 (2017)

    Article  Google Scholar 

  22. Ling, L.M., Feng, B.F., Zhu, Z.N.: Multi-soliton, multi-breather and higher order rogue wave solutions to the complex short pulse equation. Physica D 327, 13–29 (2016)

    Article  MathSciNet  Google Scholar 

  23. Tariq, K.U., Seadawy, A.R.: Bistable Bright-Dark solitary wave solutions of the(3+1)-dimensional Breaking soliton, Boussinesq equation with dual dispersion and modified Korteweg-de Vries-Kadomtsev-Petviashvili equations and their applications. Results Phys. 7, 1143–1149 (2017)

    Article  Google Scholar 

  24. Feng, B.F.: General N-soliton solution to a vector nonlinear Schrödinger equation. J. Phys. A-Math. Theor. 47(35), 355203 (2014)

    Article  Google Scholar 

  25. Bi, Y.H., Zhang, Z.G., Liu, Q.S., Liu, T.J.: Research on nonlinear waves of blood flow in arterial vessels. Commun. Nonlinear Sci. 102, 105918 (2021)

    Article  MathSciNet  Google Scholar 

  26. Hirota, R.: The Direct Method in Soliton Theory, pp. 01–58. Cambridge University Press, Cambridge (2004)

    Google Scholar 

  27. Wang, Z., Qin, Y.P., Zou, L.: Quasi-periodic solutions and asymptotic properties for the nonlocal Boussinesq equation. Chin. Phys. B 26(5), 050504 (2017)

    Article  Google Scholar 

  28. Wu, Y.Q.: Asymptotic behavior of the periodic wave solution for the (3+1)-dimensional Kadomtsev–Petviashvili equation. Appl. Math. Comput. 216(11), 3154–3161 (2010)

    MathSciNet  Google Scholar 

  29. Singh, M., Gupta, R.K.: Soliton and quasi-periodic wave solutions for b-type Kadomtsev–Petviashvili equation. Indian J. Phys. 91(11), 1345–1354 (2017)

    Article  Google Scholar 

  30. Pang, J., He, L.C., Zhao, Z.L.: On one- and two-Periodic wave solutions of the ninth-order KdV equation. Math. Notes 103(5–6), 943–951 (2018)

    Article  MathSciNet  Google Scholar 

  31. Ma, P.L., Tian, S.F.: Quasi-Periodic solutions and asymptotic properties for the isospectral BKP equation. Commun. Theor. Phys. 62(1), 17–25 (2014)

    Article  MathSciNet  Google Scholar 

  32. Zhang, Y., Cheng, Z.L., Hao, X.H.: Riemann theta function periodic wave solutions for the variable-coefficient mKdV equation. Chin. Phys. B 21(12), 120203 (2012)

    Article  Google Scholar 

  33. Nakamura, A.: A direct method of calculating periodic wave solutions to nonlinear evolution equations I. exact two-Periodic wave solution. J. Phys. Soc. Jpn. 47, 1701–1705 (1979)

    Article  MathSciNet  Google Scholar 

  34. Nakamura, A.: A direct method of calculating periodic wave solutions to nonlinear evolution equations. II. exact one- and two-Periodic wave solution of the coupled bilinear equations. J. Phys. Soc. Jpn. 48, 1365–1370 (1980)

    Article  MathSciNet  Google Scholar 

  35. Johnson, R.S.: A Modern Introduction to the Mathematical Theory of Water Waves, pp. 1–47. Cambridge University Press, Cambridge (1997)

    Google Scholar 

  36. James, R.H.: An Introduction to Dynamic Meteorology, 4th edn., pp. 229–250. Academic Press, New York (2004)

    Google Scholar 

  37. Helal, M.A., Seadawy, A.R., Zekry, M.H.: Stability analysis of solitary wave solutions for the fourth-order nonlinear Boussinesq water wave equation Appl. Math. Comput. 232, 1094–1103 (2014)

  38. Lawdenc, D.F.: Elliptic Functions and Applications. Applied Mathematical Sciences, pp. 1–20. Springer, New York (1989)

    Book  Google Scholar 

  39. Parker, A.: On exact solutions of the regularized long-wave equation: A direct approach to partially integrable equations. II. Periodic solutions. J. Math. Phys. 36(7), 3506–3519 (1995)

Download references

Funding

This work was supported by Key Laboratory of Ministry of Education for Coastal Disaster and Protection, Hohai University (No. 202201), and the National Natural Science Foundation of China (No. 41806104, 41906008).

Author information

Authors and Affiliations

  1. College of Hydraulic Science and Engineering, Yangzhou University, Yangzhou, 225009, China

    Baojun Zhao & Jiaxin Wang

  2. College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao, 266590, China

    Huanhe Dong & Lei Fu

Authors
  1. Baojun Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jiaxin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Huanhe Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Lei Fu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Baojun Zhao.

Ethics declarations

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, B., Wang, J., Dong, H. et al. Periodic solution and asymptotic behavior of the three-dimensional sixth-order Boussinesq equation in shallow water waves. Nonlinear Dyn 112, 643–659 (2024). https://doi.org/10.1007/s11071-023-09072-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-023-09072-8

Keywords

Search

Navigation