Skip to main content
SpringerLink
Log in

A memory-free formulation for determining the non-stationary response of fractional nonlinear oscillators subjected to combined deterministic and stochastic excitations

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

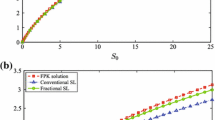
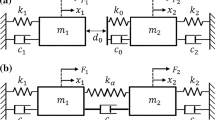
Abstract

A memory-free formulation is proposed for determining the non-stationary stochastic response of fractional single-degree-of-freedom nonlinear/hysteretic dynamic systems subjected to combined periodic and non-stationary stochastic excitations. This is achieved by decomposing the system response in a periodic and a zero-mean stochastic component, while utilizing the memory-free formulation to treat the fractional derivative terms. Specifically, first, the response decomposition leads to a system of coupled differential sub-equations of fractional order governing the deterministic and the stochastic response components. Then, invoking the memory-free formulation, the coupled system of equations is transformed into a system of deterministic and stochastic differential equations with integer-order derivatives. Next, a statistical linearization method-based framework is proposed for treating the stochastic sub-equation. This leads to the determination of the equivalent linear stochastic dynamic system, as well as of the related Lyapunov differential equation. Finally, the Lyapunov differential equation and the deterministic sub-equation with integer-order derivative are solved simultaneously using standard numerical algorithms. The applicability and accuracy of the proposed semi-analytical method is demonstrated by pertinent numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data availability

All data, models or code that supports the findings of this study is available from the corresponding author upon reasonable request.

References

  1. Podlubny, I.: Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Academic Press, San Diego, CA (1998)

    Google Scholar 

  2. Hilfer, R.: Applications of fractional calculus in physics. World Scientific Publishing Co. Pte. Ltd., Singapore (2000)

  3. Sabatier, J., Agrawal, O.P., Machado, J.T.: Advances in fractional calculus, vol. 4. Springer (2007)

  4. Cai, M., Li, C.: Numerical approaches to fractional integrals and derivatives: a review. Mathematics 8(1), 43 (2020). https://doi.org/10.3390/math8010043

    Article  MathSciNet  Google Scholar 

  5. Makris, N., Constantinou, M.: Spring-viscous damper systems for combined seismic and vibration isolation. Earthq. Eng. Struct. Dyn. 21(8), 649–664 (1992). https://doi.org/10.1002/eqe.4290210801

    Article  Google Scholar 

  6. Rossikhin, Y.A., Shitikova, M.V.: Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results. Appl. Mech. Rev. 63(1), 010801 (2009). https://doi.org/10.1115/1.4000563

    Article  Google Scholar 

  7. Di Paola, M., Pirrotta, A., Valenza, A.: Visco-elastic behavior through fractional calculus: an easier method for best fitting experimental results. Mech. Mater. 43(12), 799–806 (2011)

    Article  Google Scholar 

  8. Zhang, W., Capilnasiu, A., Sommer, G., Holzapfel, G.A., Nordsletten, D.A.: An efficient and accurate method for modeling nonlinear fractional viscoelastic biomaterials. Comput. Methods Appl. Mech. Eng. 362, 112834 (2020). https://doi.org/10.1016/j.cma.2020.112834

    Article  MathSciNet  Google Scholar 

  9. Koh, C.G., Kelly, J.M.: Application of fractional derivatives to seismic analysis of base-isolated models. Earthq. Eng. Struct. Dyn. 19(2), 229–241 (1990)

    Article  Google Scholar 

  10. Di Paola, M., Pinnola, F.P., Spanos, P.D.: Analysis of multi-degree-of-freedom systems with fractional derivative elements of rational order. In: ICFDA’14 International Conference on Fractional Differentiation and Its Applications, pp. 1–6. IEEE (2014)

  11. Pirrotta, A., Kougioumtzoglou, I.A., Di Matteo, A., Fragkoulis, V.C., Pantelous, A.A., Adam, C.: Deterministic and random vibration of linear systems with singular parameter matrices and fractional derivative terms. J. Eng. Mech. 147(6), 04021031 (2021)

    Article  Google Scholar 

  12. Chen, L., Wang, W., Li, Z., Zhu, W.: Stationary response of Duffing oscillator with hardening stiffness and fractional derivative. Int. J. Non-Linear Mech. 48, 44–50 (2013). https://doi.org/10.1016/j.ijnonlinmec.2012.08.001

    Article  Google Scholar 

  13. Spanos, P.D., Kougioumtzoglou, I.A., dos Santos, K.R.M., Beck, A.T.: Stochastic averaging of nonlinear oscillators: Hilbert transform perspective. J. Eng. Mech. 144(2), 04017173 (2018). https://doi.org/10.1061/(asce)em.1943-7889.0001410

    Article  Google Scholar 

  14. Kougioumtzoglou, I.A., Spanos, P.D.: Harmonic wavelets based response evolutionary power spectrum determination of linear and non-linear oscillators with fractional derivative elements. Int. J. Non-Linear Mech. 80, 66–75 (2016). https://doi.org/10.1016/j.ijnonlinmec.2015.11.010

    Article  Google Scholar 

  15. Spanos, P.D., Evangelatos, G.I.: Response of a non-linear system with restoring forces governed by fractional derivatives—Time domain simulation and statistical linearization solution. Soil Dyn. Earthq. Eng. 30(9), 811–821 (2010). https://doi.org/10.1016/j.soildyn.2010.01.013

    Article  Google Scholar 

  16. Fragkoulis, V.C., Kougioumtzoglou, I.A., Pantelous, A.A., Beer, M.: Non-stationary response statistics of nonlinear oscillators with fractional derivative elements under evolutionary stochastic excitation. Nonlinear Dyn. 97(4), 2291–2303 (2019). https://doi.org/10.1007/s11071-019-05124-0

    Article  Google Scholar 

  17. Di Matteo, A., Spanos, P., Pirrotta, A.: Approximate survival probability determination of hysteretic systems with fractional derivative elements. Probab. Eng. Mech. 54, 138–146 (2018). https://doi.org/10.1016/j.probengmech.2017.10.001

    Article  Google Scholar 

  18. Spanos, P.D., Malara, G.: Nonlinear random vibrations of beams with fractional derivative elements. J. Eng. Mech. 140(9), 04014069 (2014). https://doi.org/10.1061/(asce)em.1943-7889.0000778

    Article  Google Scholar 

  19. Spanos, P.D., Di Matteo, A., Cheng, Y., Pirrotta, A., Li, J.: Galerkin scheme-based determination of survival probability of oscillators with fractional derivative elements. J. Appl. Mech. 83(12), 121003 (2016). https://doi.org/10.1115/1.4034460

    Article  Google Scholar 

  20. Di Matteo, A., Kougioumtzoglou, I.A., Pirrotta, A., Spanos, P.D., Di Paola, M.: Stochastic response determination of nonlinear oscillators with fractional derivatives elements via the wiener path integral. Probab. Eng. Mech. 38, 127–135 (2014). https://doi.org/10.1016/j.probengmech.2014.07.001

    Article  Google Scholar 

  21. Petromichelakis, I., Psaros, A.F., Kougioumtzoglou, I.A.: Stochastic response analysis and reliability-based design optimization of nonlinear electromechanical energy harvesters with fractional derivative elements. J. Risk Uncertain. Eng. Syst. Part B: Mech. Eng. (2021). https://doi.org/10.1115/1.4049232

    Article  Google Scholar 

  22. Kong, F., Spanos, P.D.: Response spectral density determination for nonlinear systems endowed with fractional derivatives and subject to colored noise. Probab. Eng. Mech. 59, 103023 (2020)

    Article  Google Scholar 

  23. Kong, F., Zhang, Y., Zhang, Y.: Non-stationary response power spectrum determination of linear/non-linear systems endowed with fractional derivative elements via harmonic wavelet. Mech. Syst. Signal Process. 162, 108024 (2022). https://doi.org/10.1016/j.ymssp.2021.108024

    Article  Google Scholar 

  24. Ford, N.J., Simpson, A.C.: The numerical solution of fractional differential equations: speed versus accuracy. Num. Algorithms 26(4), 333–346 (2001). https://doi.org/10.1023/a:1016601312158

    Article  MathSciNet  Google Scholar 

  25. Yuan, L., Agrawal, O.P.: A numerical scheme for dynamic systems containing fractional derivatives. J. Vib. Acoust. 124(2), 321–324 (2002)

    Article  Google Scholar 

  26. Trinks, C., Ruge, P.: Treatment of dynamic systems with fractional derivatives without evaluating memory-integrals. Comput. Mech. 29(6), 471–476 (2002). https://doi.org/10.1007/s00466-002-0356-5

    Article  MathSciNet  Google Scholar 

  27. Diethelm, K.: An investigation of some nonclassical methods for the numerical approximation of caputo-type fractional derivatives. Num. Algorithms 47(4), 361–390 (2008). https://doi.org/10.1007/s11075-008-9193-8

    Article  MathSciNet  Google Scholar 

  28. Di Paola, M., Failla, G., Pirrotta, A.: Stationary and non-stationary stochastic response of linear fractional viscoelastic systems. Probab. Eng. Mech. 28, 85–90 (2012). https://doi.org/10.1016/j.probengmech.2011.08.017

    Article  Google Scholar 

  29. Failla, G., Pirrotta, A.: On the stochastic response of a fractionally-damped duffing oscillator. Commun. Nonlinear Sci. Numer. Simul. 17(12), 5131–5142 (2012). https://doi.org/10.1016/j.cnsns.2012.03.033

    Article  MathSciNet  Google Scholar 

  30. Zhang, Y., Kougioumtzoglou, I.A., Kong, F.: A wiener path integral technique for determining the stochastic response of nonlinear oscillators with fractional derivative elements: a constrained variational formulation with free boundaries. Prob. Eng. Mech. 71, 103410 (2023). https://doi.org/10.1016/j.probengmech.2022.103410

    Article  Google Scholar 

  31. Spanos, P.D., Zhang, W.: Nonstationary stochastic response determination of nonlinear oscillators endowed with fractional derivatives. Int. J. Non-Linear Mech. 146, 104170 (2022). https://doi.org/10.1016/j.ijnonlinmec.2022.104170

    Article  Google Scholar 

  32. Zhang, W., Spanos, P.D., Di Matteo, A.: Nonstationary stochastic response of hysteretic systems endowed with fractional derivative elements. J. Appl. Mech. 90(6), 061011 (2023). https://doi.org/10.1115/1.4056946

    Article  Google Scholar 

  33. Dai, Q., Harne, R.L.: Investigation of direct current power delivery from nonlinear vibration energy harvesters under combined harmonic and stochastic excitations. J. Intell. Mater. Syst. Struct. 29(4), 514–529 (2018)

    Article  Google Scholar 

  34. Cai, W., Harne, R.L.: Characterization of challenges in asymmetric nonlinear vibration energy harvesters subjected to realistic excitation. J. Sound Vib. 482, 115460 (2020)

    Article  Google Scholar 

  35. Pasparakis, G.D., Kougioumtzoglou, I.A., Fragkoulis, V.C., Kong, F., Beer, M.: Excitation-response relationships for linear structural systems with singular parameter matrices: a periodized harmonic wavelet perspective. Mech. Syst. Signal Process. 169, 108701 (2022)

    Article  Google Scholar 

  36. Davenport, A.: The response of slender structures to wind. In: Wind Climate in Cities, pp. 209–239. Springer (1995)

  37. Tessari, R.K., Kroetz, H.M., Beck, A.T.: Performance-based design of steel towers subject to wind action. Eng. Struct. 143, 549–557 (2017)

    Article  Google Scholar 

  38. Spanos, P.D., Zhang, Y., Kong, F.: Formulation of statistical linearization for m-d-o-f systems subject to combined periodic and stochastic excitations. J. Appl. Mech. 86(10), 101003 (2019). https://doi.org/10.1115/1.4044087

    Article  Google Scholar 

  39. Zhang, Y., Spanos, P.D.: Efficient response determination of a M-D-O-F gear model subject to combined periodic and stochastic excitations. Int. J. Non-Linear Mech. 120, 103378 (2020). https://doi.org/10.1016/j.ijnonlinmec.2019.103378

    Article  Google Scholar 

  40. Zhang, Y., Spanos, P.D.: A linearization scheme for vibrations due to combined deterministic and stochastic loads. Probab. Eng. Mech. 60, 103028 (2020). https://doi.org/10.1016/j.probengmech.2020.103028

    Article  Google Scholar 

  41. Kong, F., Spanos, P.D.: Stochastic response of hysteresis system under combined periodic and stochastic excitation via the statistical linearization method. J. Appl. Mech. 88(5), 1–12 (2021)

    Article  Google Scholar 

  42. Ni, P., Fragkoulis, V.C., Kong, F., Mitseas, I.P., Beer, M.: Response determination of nonlinear systems with singular matrices subject to combined stochastic and deterministic excitations. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A: Civ. Eng. 7(4), 04021049 (2021). https://doi.org/10.1061/ajrua6.0001167

  43. Kong, F., Han, R., Zhang, Y.: Approximate stochastic response of hysteretic system with fractional element and subjected to combined stochastic and periodic excitation. Nonlinear Dyn. (2021). https://doi.org/10.1007/s11071-021-07014-w

    Article  Google Scholar 

  44. Kong, F., Han, R., Li, S., He, W.: Non-stationary approximate response of non-linear multi-degree-of-freedom systems subjected to combined periodic and stochastic excitation. Mech. Syst. Signal Process. 166, 108420 (2022). https://doi.org/10.1016/j.ymssp.2021.108420

    Article  Google Scholar 

  45. Schmidt, A., Gaul, L.: On a critique of a numerical scheme for the calculation of fractionally damped dynamical systems. Mech. Res. Commun. 33(1), 99–107 (2006). https://doi.org/10.1016/j.mechrescom.2005.02.018

    Article  Google Scholar 

  46. Diethelm, K.: An improvement of a nonclassical numerical method for the computation of fractional derivatives. J. Vib. Acoust. 131(1), 014502 (2009). https://doi.org/10.1115/1.2981167

    Article  Google Scholar 

  47. Birk, C., Song, C.: An improved non-classical method for the solution of fractional differential equations. Comput. Mech. 46(5), 721–734 (2010). https://doi.org/10.1007/s00466-010-0510-4

    Article  MathSciNet  Google Scholar 

  48. Liu, Q.X., Chen, Y.M., Liu, J.K.: An improved Yuan-Agrawal method with rapid convergence rate for fractional differential equations. Comput. Mech. 63(4), 713–723 (2018). https://doi.org/10.1007/s00466-018-1621-6

    Article  MathSciNet  Google Scholar 

  49. Roberts, J.B., Spanos, P.D.: Random vibration and statistical linearization. Courier Corporation (2003)

  50. Kougioumtzoglou, I.A., Fragkoulis, V.C., Pantelous, A.A., Pirrotta, A.: Random vibration of linear and nonlinear structural systems with singular matrices: a frequency domain approach. J. Sound Vib. 404, 84–101 (2017). https://doi.org/10.1016/j.jsv.2017.05.038

    Article  Google Scholar 

  51. Shinozuka, M., Deodatis, G.: Simulation of stochastic processes by spectral representation. Appl. Mech. Rev. 44(4), 191–204 (1991). https://doi.org/10.1115/1.3119501

    Article  MathSciNet  Google Scholar 

  52. Ismail, M., Ikhouane, F., Rodellar, J.: The hysteresis Bouc-Wen model, a survey. Archiv. Comput. Methods Eng. 16(2), 161–188 (2009)

    Article  Google Scholar 

Download references

Acknowledgements

The corresponding author would like to express his gratitude to professor Fan Kong at Hefei University of Technology and doctor Vasileios C. Fragkoulis at the University of Liverpool for their insightful advice. This work was supported by the National Natural Science Foundation of China (Grant no. 52078399).

Funding

This work was supported by the National Natural Science Foundation of China (Grant no. 52078399).

Author information

Authors and Affiliations

  1. College of Civil Engineering, Tongji University, 1239 Siping Road, Shanghai, 200092, China

    Renjie Han

Authors
  1. Renjie Han
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Renjie Han.

Ethics declarations

Competing Interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Han, R. A memory-free formulation for determining the non-stationary response of fractional nonlinear oscillators subjected to combined deterministic and stochastic excitations. Nonlinear Dyn 111, 22363–22379 (2023). https://doi.org/10.1007/s11071-023-08984-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-023-08984-9

Keywords

Search

Navigation