Nondegenerate soliton dynamics of nonlocal nonlinear Schrödinger equation

Abstract

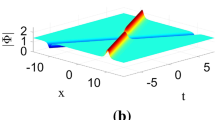
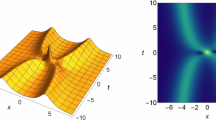
We obtain the nondegenerate one- and two-soliton solutions of the nonlocal nonlinear Schrödinger equation by using the nonstandard Hirota method. This unconventional method is used to bilinearize the nonlocal nonlinear Schrödinger equation and its related auxiliary equations, and some novel interaction properties of parity-time-symmetric two-soliton solutions are derived. The detailed asymptotic analysis is used to reveal the characteristics of energy conservation and energy redistribution before and after the collision between nondegenerate solitons. Experimental scheme to observe nondegenerate solitons is also proposed. This provides potential applications for the soliton interaction in the nonlocal wave model.

Appendix parameters in solutions (9) and (11)

1.1 I. Parameters in solution (9)

$$ \eta_{j} = i\kappa_{j} x + i\kappa_{j}^{2} t,\overline{\eta }_{j} = i\overline{\kappa }_{j} x - i\overline{\kappa }_{j}^{2} t,\xi_{j} = i\iota_{j} x + i\iota_{j}^{2} t,\overline{\xi }_{j} = i\overline{\iota }_{j} x - i\overline{\iota }_{j}^{2} t $$

$$ \begin{gathered} \eta_{jR} = - \kappa_{jI} (x + 2\kappa_{jR} t),\eta_{jI} = \kappa_{jR} x + (\kappa_{jR}^{2} - \kappa_{jI}^{2} )t,\xi_{jR} = - \iota_{jI} (x + 2\iota_{jR} t),\xi_{jI} = \iota_{jR} x + (\iota_{jR}^{2} - \iota_{jI}^{2} )t, \hfill \\ A_{1}^{1} = \frac{{\sigma \alpha_{1} \alpha_{2} \overline{\alpha }_{2} ( - \overline{\iota }_{1} - 2\kappa_{1} + \iota_{1} )}}{{(\kappa_{1} + \overline{\iota }_{1} )(\overline{\iota }_{1} + \iota_{1} )^{2} }},A_{{_{1} }}^{2} = \frac{{\sigma \alpha_{1} \alpha_{2} \overline{\alpha }_{1} ( - \overline{\kappa }_{1} - 2\iota_{1} + \kappa_{1} )}}{{(\overline{\kappa }_{1} + \iota_{1} )(\overline{\kappa }_{1} + \kappa_{1} )^{2} }},B_{{_{1} }}^{j} = - \frac{{2\sigma \alpha_{1} \overline{\alpha }_{1} }}{{(\overline{\kappa }_{1} + \kappa_{1} )^{2} }},B_{{_{2} }}^{j} = - \frac{{2\sigma \alpha_{2} \overline{\alpha }_{2} }}{{(\overline{\iota }_{1} + \iota_{1} )^{2} }}, \hfill \\ \end{gathered} $$

$$ \begin{gathered} C_{1}^{1} = \frac{{ - B_{{_{2} }}^{1} B_{{_{1} }}^{1} (\overline{\kappa }_{1} + \kappa_{1} - \overline{\iota }_{1} - \iota_{1} )^{2} - 2(A_{1}^{1} \overline{\alpha }_{1} + A_{{_{1} }}^{2} \overline{\alpha }_{2} + \overline{A}_{1}^{1} \alpha_{1} )}}{{(\overline{\kappa }_{1} + \kappa_{1} + \overline{\iota }_{1} + \iota_{1} )^{2} }},N_{m}^{n} { = } - \frac{{2\sigma \alpha_{mn} \overline{\alpha }_{mn} }}{{(\overline{\kappa }_{n} + \kappa_{m} )^{2} }}{\text{,P}}_{m}^{n} = - \frac{{2\sigma \alpha_{mn} \overline{\alpha }_{mn} }}{{(\overline{\iota }_{n} + \iota_{m} )^{2} }} \hfill \\ C_{{_{1} }}^{2} = \frac{{ - \overline{B}_{{_{2} }}^{1} \overline{B}_{{_{1} }}^{1} (\overline{\kappa }_{1} + \kappa_{1} - \overline{\iota }_{1} - \iota_{1} )^{2} - 2\sigma (A_{1}^{1} \overline{\alpha }_{1} + A_{{_{1} }}^{2} \overline{\alpha }_{2} + \overline{A}_{1}^{1} \alpha_{1} + \overline{A}_{{_{1} }}^{2} \alpha_{2} )}}{{(\overline{\kappa }_{1} + \kappa_{1} + \overline{\iota }_{1} + \iota_{1} )^{2} }}, \hfill \\ \end{gathered} $$

1.2 II. Parameters in solution (11)

$$ \begin{gathered} D_{m}^{n(p)} = \frac{{\sigma ( - 2\kappa_{1n} - \overline{\kappa }_{2p} + \kappa_{2m} )\alpha_{m2} \alpha_{n1} \alpha_{p20} }}{{(\kappa_{2m} + \overline{\kappa }_{2p} )^{2} (\kappa_{1n} + \overline{\kappa }_{2p} )}},d_{m}^{n\left( p \right)} = \frac{{\sigma ( - 2\kappa_{2n} - \overline{\kappa }_{1p} + \kappa_{1m} )\alpha_{m1} \alpha_{n2} \overline{\alpha }_{p1} }}{{(\kappa_{1m} + \overline{\kappa }_{1p} )^{2} (\kappa_{2n} + \overline{\kappa }_{1p} )}} \hfill \\ E_{m}^{n} = - \frac{{2\sigma \alpha_{2n} \alpha_{1n} \overline{\alpha }_{mn} [(\kappa_{n1} + \kappa_{n2} + \overline{\kappa }_{nm} )\overline{\kappa }_{nm} + \kappa_{n1}^{2} + \kappa_{n2}^{2} - \kappa_{n1} \kappa_{n2} ]}}{{(\kappa_{n2} + \overline{\kappa }_{nm} )^{2} (\overline{\kappa }_{nm} + \kappa_{n1} )^{2} }} \hfill \\ \end{gathered} $$

$$ \begin{gathered} F_{1M2N}^{mn} = - \frac{1}{{(\kappa_{1M} + \kappa_{2N} + \overline{\kappa }_{1m} + \overline{\kappa }_{2n} )}}(\sigma d_{M}^{M(m)} d_{N}^{P(N)} (\kappa_{1M} - \kappa_{2N} + \overline{\kappa }_{1m} - \overline{\kappa }_{2n} )^{2} + F + \overline{F}), \hfill \\ F_{n} = - \frac{1}{{(F_{3} + \overline{F}_{3} )}}(\sigma d_{1}^{n(1)} d_{1}^{n(2)} (\kappa_{n1} - \kappa_{n2} + \overline{\kappa }_{n1} - \overline{\kappa }_{n2} )^{2} + F_{4} + \overline{F}_{4} ),F = 2E_{1}^{n} \overline{\alpha }_{2n} + 2E_{2}^{n} \overline{\alpha }_{1n} , \hfill \\ P \ne N,F_{3} = \kappa_{n1} + \kappa_{n2} ,F_{4} = 2D_{N}^{M(n)} \overline{\alpha }_{m1} + 2d_{M}^{N(m)} \overline{\alpha }_{n2} . \hfill \\ \end{gathered} $$

$$ \begin{gathered} J_{1M2m}^{mn} = \frac{1}{{2[(J_{1}^{ + } + \kappa_{2n} + \overline{\kappa }_{1M} )\overline{\kappa }_{1M} + (J_{1}^{ + } + J_{2}^{2 + } + \overline{\kappa }_{1M} )\overline{\kappa }_{2m} + J_{1}^{ + } \kappa_{2n} + \kappa_{11} \kappa_{12} ]}}\sum\limits_{p = 1}^{2} { - 2\{ [J_{2}^{1 + } + ( - 1)^{p - 1} J_{1}^{ - } ]\overline{\kappa }_{2m} + [\kappa_{2n} + ( - 1)^{p - 1} J_{1}^{ - } ]\overline{\kappa }_{1M} } \hfill \\ + \kappa_{2n}^{2} + ( - 1)^{p - 1} J_{1}^{ - } (\kappa_{11} + \kappa_{2n} )\} \alpha_{q1} F_{1p2n}^{Mm} - \sigma^{2} X\sum\limits_{p = 1}^{2} {d_{p}^{p(M)} \alpha_{P1} [(\kappa_{1Q} + \overline{\kappa }_{1M} )^{2} + (J_{2}^{2 + } )^{2} ] - 2\sigma \{ D[ - \frac{1}{2}\overline{\kappa }_{1M}^{2} - \kappa_{11} \kappa_{12} + J_{2}^{2 + } (J_{1}^{ - } + \overline{\kappa }_{2m} - } \hfill \\ \overline{\kappa }_{1M} )] + [(J_{1}^{ + } - J_{2}^{2 + } + \overline{\kappa }_{1M} )\overline{\kappa }_{1M} - (J_{1}^{ + } + \frac{{\overline{\kappa }_{2m} }}{2})\overline{\kappa }_{2m} + (\kappa_{12} - \kappa_{2n} )\kappa_{11} - (\kappa_{12} - \frac{{\kappa_{2n} }}{2})\kappa_{2n} ]E_{M}^{1} X + \frac{1}{2}\sum\limits_{p = 1}^{2} {D_{n}^{P(m)} d_{p}^{p(M)} (\kappa_{1Q}^{2} - 2\kappa_{1P} \overline{\kappa }_{NM} ) + 2} \hfill \\ \overline{D}_{m}^{M(n)} \alpha_{21} \alpha_{11} + \sum\limits_{p = 1}^{2} {D_{n}^{p(m)} \overline{\alpha }_{M1} + \overline{d}_{M}^{m(p)} \alpha_{n2} + d_{p}^{n(M)} \overline{\alpha }_{m2} )\alpha_{q1} \} ,J_{1}^{ \pm } = \kappa_{11} \pm \kappa_{12} ,J_{2}^{p + } = \kappa_{2n} + \overline{\kappa }_{pm} } . \hfill \\ \end{gathered} $$

$$ \begin{gathered} j_{1M2m}^{mn} = \frac{1}{{2[(j_{1}^{ + } + \kappa_{2n} + \overline{\kappa }_{1M} )\overline{\kappa }_{1M} + (j_{1}^{ + } + j_{2}^{2 + } + \overline{\kappa }_{1M} )\overline{\kappa }_{2m} + j_{1}^{ + } \kappa_{2n} + \kappa_{11} \kappa_{12} ]}}\sum\limits_{p = 1}^{2} { - 2\{ [j_{2}^{1 + } + ( - 1)^{p - 1} j_{1}^{ - } ]\overline{\kappa }_{2m} + [\kappa_{2n} + ( - 1)^{p - 1} j_{1}^{ - } ]\overline{\kappa }_{1M} } \hfill \\ + \kappa_{2n}^{2} + ( - 1)^{p - 1} j_{1}^{ - } (\kappa_{11} + \kappa_{2n} )\} \alpha_{q1} F_{1p2n}^{Mm} - \sigma^{2} X\sum\limits_{p = 1}^{2} {d_{p}^{p(M)} \alpha_{P1} [(\kappa_{1Q} + \overline{\kappa }_{1M} )^{2} + (j_{2}^{2 + } )^{2} ] - 2\sigma \{ D[ - \frac{1}{2}\overline{\kappa }_{1M}^{2} - \kappa_{11} \kappa_{12} + j_{2}^{2 + } (j_{1}^{ - } + \overline{\kappa }_{2m} - } \hfill \\ \overline{\kappa }_{1M} )] + [(j_{1}^{ + } - j_{2}^{2 + } + \overline{\kappa }_{1M} )\overline{\kappa }_{1M} - (j_{1}^{ + } + \frac{{\overline{\kappa }_{2m} }}{2})\overline{\kappa }_{2m} + (\kappa_{12} - \kappa_{2n} )\kappa_{11} - (\kappa_{12} - \frac{{\kappa_{2n} }}{2})\kappa_{2n} ]E_{M}^{2} X + \frac{1}{2}\sum\limits_{p = 1}^{2} {d_{n}^{P(m)} D_{p}^{p(M)} (\kappa_{1Q}^{2} - 2\kappa_{1P} \overline{\kappa }_{NM} ) + 2} \hfill \\ \overline{d}_{m}^{M(n)} \alpha_{21} \alpha_{11} + \sum\limits_{p = 1}^{2} {d_{n}^{p(m)} \overline{\alpha }_{M1} + \overline{D}_{M}^{m(p)} \alpha_{n2} + D_{p}^{n(M)} \overline{\alpha }_{m2} )\alpha_{q1} \} ,j_{1}^{ \pm } = \kappa_{11} \pm \kappa_{12} ,j_{2}^{p + } = \kappa_{2n} + \overline{\kappa }_{pm} } . \hfill \\ \end{gathered} $$

$$ D = D_{n}^{M(m)} d_{2}^{2(M)} + D_{n}^{N(m)} d_{1}^{1(M)} ,P = \left\{ {\begin{array}{*{20}c} {M,p = 2} \\ {N,p = 1} \\ \end{array} } \right.,Q \ne P,p \ne q,X = \left\{ {\begin{array}{*{20}c} {d121,m = 1,n = 1} \\ {d212,m = 1,n = 2} \\ \end{array} } \right.o{\text{r }}X = \left\{ {\begin{array}{*{20}c} {d211,m = 2,n = 1} \\ {d122,m = 2,n = 2} \\ \end{array} } \right.. $$

$$ \begin{gathered} H_{mn}^{1} = - \frac{1}{{(\kappa_{11} + \kappa_{12} + \kappa_{2m} + \kappa_{110} + \kappa_{120} + \kappa_{2n0} )}}(\sigma \{ F1[X( - \kappa_{11} - \kappa_{12} + \kappa_{2m} - \kappa_{110} - \kappa_{120} + \kappa_{2n0} )^{2} + 2\alpha_{m2} \overline{\alpha }_{n2} ] + F_{1q2m}^{Nn} \hfill \\ [d_{p}^{p(M)} (\kappa_{11} - \kappa_{12} - ( - 1)^{q} \kappa_{2m} + ( - 1)^{N} (\kappa_{110} - \kappa_{120} ) - ( - 1)^{q} \kappa_{2n0} )^{2} + 2\alpha_{p1} \overline{\alpha }_{M1} ] + Y + \overline{Y} + 2d_{2}^{1(1)} \overline{d}_{2}^{1(1)} + 2d_{1}^{1(2)} \overline{d}_{1}^{1(2)} \} ), \hfill \\ Y = 2\alpha_{12} \overline{j}_{2122}^{1} + 2(\sum\limits_{M = 1}^{2} {} \alpha_{m1} \overline{J}_{1N21}^{11} + \overline{D}_{1}^{M(1)} E_{N}^{1} ) + 2d_{2}^{1(2)} \overline{d}_{1}^{1(1)} ,M \ne N,p \ne q. \hfill \\ \end{gathered} $$

$$ \begin{gathered} H_{mn}^{2} = - \frac{1}{{(\kappa_{21} + \kappa_{1n} + \kappa_{22} + \kappa_{1m0} + \kappa_{210} + \kappa_{220} )}}(\sigma \{ F2[X( - \kappa_{1n} + \kappa_{21} + \kappa_{22} - \kappa_{1m0} + \kappa_{210} + \kappa_{220} )^{2} + 2\alpha_{n1} \overline{\alpha }_{m1} ] + F_{1q2m}^{Nn} \hfill \\ [X(\kappa_{11} - \kappa_{21} - ( - 1)^{q} \kappa_{1n} + ( - 1)^{N} (\kappa_{210} - \kappa_{220} ) - ( - 1)^{q} \kappa_{1m0} )^{2} + 2\alpha_{p2} \overline{\alpha }_{M2} ] + y + \overline{y} + 2D_{2}^{1(1)} \overline{D}_{2}^{1(1)} + 2D_{1}^{1(2)} \overline{D}_{1}^{1(2)} \} ), \hfill \\ y = 2\alpha_{11} \overline{J}_{2122}^{1} + 2(\sum\limits_{M = 1}^{2} {} \alpha_{m2} \overline{j}_{1N21}^{11} + \overline{d}_{1}^{M(1)} E_{N}^{2} ) + 2D_{2}^{1(2)} \overline{D}_{1}^{1(1)} ,M \ne N,p \ne q. \hfill \\ \end{gathered} $$

$\begin{gathered} K_{m} = \sum\limits_{\begin{subarray}{l} m,n, \\ p,q = 1 \end{subarray} }^{2} {} F_{11}^{2n(1m)} \{ - 2d_{m}^{p(q)} \alpha_{21} (k_{2q} + \overline{k}_{2p} )(k_{11} + \overline{k}_{11} + k_{2n} + \overline{k}_{2m} )\sigma - D_{q}^{2(p)} [2(K_{2} - \overline{k}_{11} - \overline{k}_{2m} + \overline{k}_{2p} )\overline{k}_{2p} + 2(K_{2} - \overline{k}_{11} - \overline{k}_{2m} )k_{12} + \hfill \\ 2( - k_{11} - k_{2n} - \overline{k}_{11} - \overline{k}_{2m} )k_{2q} + k_{11}^{2} + k_{2n}^{2} - \overline{k}_{11}^{2} - \overline{k}_{2m}^{2} ]\} + \sum\limits_{\begin{subarray}{l} m,n, \\ p,q = 1 \end{subarray} }^{2} {} F_{12}^{2n(1m)} \{ - 2d_{m}^{p(q)} \alpha_{11} (k_{2q} + \overline{k}_{2p} )(k_{12} + \overline{k}_{11} + k_{2n} + \overline{k}_{2m} )\sigma - D_{q}^{1(p)} [(K_{2} \hfill \\ + \overline{k}_{11} + \overline{k}_{2m} - \overline{k}_{2p} )\overline{k}_{2p} + (k_{12} + k_{21} - k_{22} + \overline{k}_{11} + \overline{k}_{2m} )k_{11} + (k_{12} + k_{2n} + \overline{k}_{11} + \overline{k}_{2m} )k_{2q} + \frac{1}{2}( - k_{12}^{2} - k_{2n}^{2} + \overline{k}_{11}^{2} + \overline{k}_{2m}^{2} )]\} + \sum\limits_{\begin{subarray}{l} m,n, \\ p,q = 1 \end{subarray} }^{2} {} - 2XJ_{11}^{2q(qp)} \hfill \\ \sigma [(K_{2} + \overline{k}_{11} + \overline{k}_{21} - \overline{k}_{22} )\overline{k}_{2p} + ( - k_{11} - k_{12} - k_{2p} - \overline{k}_{11} )\overline{k}_{2n} + K_{1} \overline{k}_{11} + (k_{11} + k_{12} - k_{22} )k_{21} - (k_{11} + k_{12} )k_{22} + k_{11} k_{12} + \frac{1}{2}(k_{2m}^{2} - \overline{k}_{22}^{2} + 2\overline{k}_{11}^{2} )] \hfill \\ /2[(K_{1} + \overline{k}_{11} + \overline{k}_{21} + \overline{k}_{q1}^{2} + \overline{k}_{22} )\overline{k}_{q1} + (K_{1} + \overline{k}_{nm} + \overline{k}_{q2} )\overline{k}_{q2} + (K_{1} + \overline{k}_{nm} )\overline{k}_{nm} + (k_{1n} + k_{12} + k_{22} )k_{q1} + (k_{n1} + k_{n2} )k_{q2} + k_{n1} k_{n2} ], \hfill \\ \end{gathered}$ $\begin{gathered} M = \sum\limits_{\begin{subarray}{l} m,n, \\ p,q = 1 \end{subarray} }^{2} {} - [(k_{11} + k_{12} - k_{21} + k_{22} + \overline{k}_{11} + \overline{k}_{12} + \overline{k}_{21} - \overline{k}_{22} )^{2} d_{q}^{n(m)} + 2\alpha_{np} \overline{\alpha }_{qp} ]\sigma H_{q}^{n(m)} - (k_{11} + k_{12} - k_{21} - k_{22} + \overline{k}_{11} + \overline{k}_{12} - \overline{k}_{21} - \overline{k}_{22} )^{2} F_{1} F_{2} \hfill \\ - 2\sum\limits_{\begin{subarray}{l} m,n,p \\ q,M,N = 1 \end{subarray} }^{2} {} [( - \alpha_{11} d_{n}^{q(M)} \overline{\alpha }_{m1} - \alpha_{M2} d_{n}^{n(n)} \overline{\alpha }_{n2} ) + M_{1} + \overline{M}_{1} ]\sigma F_{12}^{2N(pq)} - 2\sigma [\sum\limits_{\begin{subarray}{l} m,n,p \\ q,M,N = 1 \end{subarray} }^{2} {} (M_{2} + \overline{M}_{2} )] - (k_{11} - k_{12} + k_{21} - k_{22} + \overline{k}_{11} - \overline{k}_{12} + \overline{k}_{21} - \overline{k}_{22} )^{2} F_{12}^{2N(pq)} \hfill \\ - 2\sigma [( - \alpha_{NM} d_{n}^{q(2)} \overline{\alpha }_{pM} - \alpha_{2P} d_{m}^{m(p)} \overline{\alpha }_{qp} )\sigma + M_{3} + \overline{M}_{3} ]F_{11}^{2M(mn)} ,M_{1} = D_{M}^{1(n)} \overline{\alpha }_{m1} + d_{1}^{M(m)} \overline{\alpha }_{n2} ,M_{2} = D_{m}^{n(M)} \overline{J}_{1q}^{2p(pN)} + d_{m}^{n(M)} \overline{j}_{1q}^{2p(pN)} + \overline{E}_{m}^{n} \overline{J}_{21}^{22(p)} . \hfill \\ M_{3} = D_{N}^{2(q)} \overline{\alpha }_{p1} + d_{N}^{N(p)} \overline{\alpha }_{q2} . \hfill \\ \end{gathered}$ $\begin{gathered} L_{m} = \sum\limits_{\begin{subarray}{l} m,n, \\ p,q = 1 \end{subarray} }^{2} {} F_{11}^{2n(1m)} \{ - 2d_{m}^{p(q)} \alpha_{21} (k_{2q} + \overline{k}_{2p} )(k_{11} + \overline{k}_{11} + k_{2n} + \overline{k}_{2m} )\sigma - d_{q}^{2(p)} [2(K_{2} - \overline{k}_{11} - \overline{k}_{2m} + \overline{k}_{2p} )\overline{k}_{2p} + 2( - k_{11} - k_{21} + k_{22} - \overline{k}_{11} - \overline{k}_{2m} )k_{12} \hfill \\ + 2( - k_{11} - k_{2n} - \overline{k}_{11} - \overline{k}_{2m} )k_{2q} + k_{11}^{2} + k_{2n}^{2} - \overline{k}_{11}^{2} - \overline{k}_{2m}^{2} ]\} + \sum\limits_{\begin{subarray}{l} m,n, \\ p,q = 1 \end{subarray} }^{2} {} F_{12}^{2n(1m)} \{ - 2d_{m}^{p(q)} \alpha_{11} (k_{2q} + \overline{k}_{2p} )(k_{12} + \overline{k}_{11} + k_{2n} + \overline{k}_{2m} )\sigma - d_{q}^{1(p)} [(K_{1} + \overline{k}_{11} + \hfill \\ \overline{k}_{2m} - \overline{k}_{2p} )\overline{k}_{2p} + (k_{12} + k_{21} - k_{22} + \overline{k}_{11} + \overline{k}_{2m} )k_{11} + (k_{12} + k_{2n} + \overline{k}_{11} + \overline{k}_{2m} )k_{2q} + \frac{1}{2}( - k_{12}^{2} - k_{2n}^{2} + \overline{k}_{11}^{2} + \overline{k}_{2m}^{2} )]\} + \sum\limits_{\begin{subarray}{l} m,n, \\ p,q = 1 \end{subarray} }^{2} {} - 2Xj_{11}^{2q(qp)} \sigma [(K_{1} + \overline{k}_{11} + \hfill \\ \overline{k}_{21} - \overline{k}_{22} )\overline{k}_{2p} + ( - k_{11} - k_{12} - k_{2p} - \overline{k}_{11} )\overline{k}_{2n} + L_{1} \overline{k}_{11} + (k_{11} + k_{12} - k_{22} )k_{21} - (k_{11} + k_{12} )k_{22} + k_{11} k_{12} + \frac{1}{2}(k_{2m}^{2} - \overline{k}_{22}^{2} + 2\overline{k}_{11}^{2} )]/2[(K_{1} + \overline{k}_{11} + \overline{k}_{21} + \hfill \\ \overline{k}_{q1}^{2} + \overline{k}_{22} )\overline{k}_{q1} + (K_{1} + \overline{k}_{nm} + \overline{k}_{q2} )\overline{k}_{q2} + (K_{1} + \overline{k}_{nm} )\overline{k}_{nm} + (k_{1n} + k_{12} + k_{22} )k_{q1} + (k_{n1} + k_{n2} )k_{q2} + k_{n1} k_{n2} ],m \ne n,p \ne q,K_{1} = k_{11} + k_{12} + k_{21} + k_{22} , \hfill \\ K_{2} = - k_{11} + k_{12} + k_{21} - k_{22} . \hfill \\ \end{gathered}$